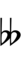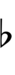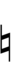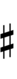12edo
| ← 11edo | 12edo | 13edo → |
(convergent)
12 equal divisions of the octave (abbreviated 12edo or 12ed2), also called 12-tone equal temperament (12tet) or 12 equal temperament (12et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 12 equal parts of exactly 100 ¢ each. Each step represents a frequency ratio of 21/12, or the 12th root of 2. It is the predominating tuning system in the world today.
Theory
12edo achieved its position as the standard Western tuning system through a combination of theoretical properties and practicality. It is the smallest number of equal divisions of the octave (edo) which can seriously claim to represent 5-limit harmony, and because it represents a meantone temperament (specifically 1⁄12 Pythagorean comma meantone, or approximately 1⁄11 syntonic comma or full schisma meantone).
It divides the octave into twelve equal parts, each of exactly 100 cents each unless octave stretching or compression is employed. It has a fifth which is quite accurate at 700 cents, two cents flat of just. It has a major third which is 13.7 cents sharp of just, which, while reasonable for its size, is unsatisfactory for some. The minor third is flat of just by even more, 15.6 cents.
Historically, 12edo became dominant primarily due to practical considerations for keyboard instruments and its ability to handle modulation across all keys with reasonable intonation. In actual performance, these deviations from just intonation are often reduced by the tuning adaptations of skilled performers. Modern music theory has increasingly treated 12edo as a system in its own right rather than as an approximation of just intonation or meantone, leading to theoretical approaches such as serialism and much of jazz harmony that derive from 12edo's structure as an equal division rather than its underlying temperament properties.[citation needed]
12edo is the basic example of a dodecatonic scale and can be considered the simplest well temperament, where all twelve fifths are the same.
The 7th harmonic (7/4) is represented by the diatonic minor seventh, which is sharp by 31 cents, and as such 12edo tempers out 64/63. The deviation explains why minor sevenths tend to stand out distinctly from the rest of the chord in a tetrad. Such tetrads are often used as dominant seventh chords in functional harmony, for which the 5-limit JI version would be 1–5/4–3/2–16/9, and while 12et officially supports septimal meantone for tempering out 126/125 and 225/224 via its patent val of ⟨12 19 28 34], its approximations of 7-limit intervals are not very accurate. It cannot be said to represent 11 or 13 at all, though it does a quite credible 17 and an even better 19. Nevertheless, its relative tuning accuracy is quite high, and 12edo is the fourth zeta integral edo.
Stacking the fifth twelve times returns the pitch to the starting point, so that the Pythagorean comma, 312/219, is tempered out. Three major thirds equal an octave, so the lesser diesis, 128/125, is tempered out. Four minor thirds also equal an octave, so the greater diesis, 648/625, is tempered out. These features have been widely utilized in contemporary music. Other commas 12et tempers out include the diaschisma, 2048/2025, the septimal quartertone, 36/35, and the jubilisma, 50/49. Each affects the structure of 12et in specific ways, and tuning systems which share the comma in question will be similar to 12et in precisely those ways.
12edo also offers very good approximations to intervals in the 2.3.17.19 subgroup. This indicates one way to use 12edo that deviates from common-practice harmony; for instance the cluster chord 8:17:36:76 is well represented.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -1.96 | +13.69 | +31.17 | +48.68 | -40.53 | -4.96 | +2.49 | -28.27 | -29.58 | -45.04 |
| Relative (%) | +0.0 | -2.0 | +13.7 | +31.2 | +48.7 | -40.5 | -5.0 | +2.5 | -28.3 | -29.6 | -45.0 | |
| Steps (reduced) |
12 (0) |
19 (7) |
28 (4) |
34 (10) |
42 (6) |
44 (8) |
49 (1) |
51 (3) |
54 (6) |
58 (10) |
59 (11) | |
Subsets and supersets
12edo contains 2edo, 3edo, 4edo, and 6edo as subsets. It is the 5th highly composite edo, 12 being both a superabundant and a highly composite number. 12edo is also the only known edo aside from 2edo that is both strict zeta and highly composite.
24edo, which doubles it, improves significantly on approximations to 11 and 13, with 13 tuned sharp. 36edo, which triples it, improves on harmonics 7 and 13, but has the 13 tuned flat instead of sharp. 72edo is a notable zeta-record edo, and 60-, 84-, and 96edo all see utilities. Notable rank-2 temperaments that augment 12edo with extra generators include compton and catler.
Intervals
| Degree | Cents | Interval region | Approximated JI intervals[note 1] (error in ¢) | Audio | |||
|---|---|---|---|---|---|---|---|
| 3-limit | 5-limit | 7-limit | Other | ||||
| 0 | 0 | Unison (prime) | 1/1 (just) | ||||
| 1 | 100 | Minor second | 25/24 (+29.328) 16/15 (−11.731) |
28/27 (+37.039) 21/20 (+15.533) 15/14 (−19.443) |
18/17 (+1.045) 17/16 (−4.955) |
||
| 2 | 200 | Major second | 9/8 (−3.910) | 10/9 (+17.596) | 28/25 (+3.802) 8/7 (−31.174) |
19/17 (+7.442) 55/49 (+0.020) 64/57 (−0.532) 17/15 (−16.687) |
|
| 3 | 300 | Minor third | 32/27 (+5.865) | 6/5 (−15.641) | 7/6 (+33.129) 25/21 (−1.847) |
19/16 (+2.487) 44/37 (+0.026) |
|
| 4 | 400 | Major third | 81/64 (−7.820) | 5/4 (+13.686) | 63/50 (−0.108) 9/7 (−35.084) |
34/27 (+0.910) 24/19 (−4.442) |
|
| 5 | 500 | Fourth | 4/3 (+1.955) | ||||
| 6 | 600 | Tritone | 45/32 (+9.776) 64/45 (−9.776) |
7/5 (+17.488) 10/7 (−17.488) |
24/17 (+3.000) 99/70 (−0.088) 17/12 (−3.000) |
||
| 7 | 700 | Fifth | 3/2 (−1.955) | ||||
| 8 | 800 | Minor sixth | 128/81 (+7.820) | 8/5 (−13.686) | 14/9 (+35.084) 100/63 (+0.108) |
19/12 (+4.442) 27/17 (−0.910) |
|
| 9 | 900 | Major sixth | 27/16 (−5.865) | 5/3 (+15.641) | 42/25 (+1.847) 12/7 (−33.129) |
37/22 (−0.026) 32/19 (−2.487) |
|
| 10 | 1000 | Minor seventh | 16/9 (+3.910) | 9/5 (−17.596) | 7/4 (+31.174) 25/14 (−3.802) |
30/17 (+16.687) 57/32 (+0.532) 98/55 (−0.020) 34/19 (−7.442) |
|
| 11 | 1100 | Major seventh | 15/8 (+11.731) 48/25 (−29.328) |
28/15 (+19.443) 40/21 (−15.533) 27/14 (−37.039) |
32/17 (+4.955) 17/9 (−1.045) |
||
| 12 | 1200 | Octave | 2/1 (just) | ||||
Notation
12edo intervals and notes have standard names from classical music theory. This classical notation system, which was in use before 12edo with other tuning systems based on chains of fifths, is sometimes called the chain-of-fifths notation or extended Pythagorean notation.
| Semitones | −2 | −1 | 0 | +1 | +2 |
|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
1edo, 2edo, 3edo, 4edo and 6edo can all be written using 12edo subset notation.
Any 12edo note or interval can be respelled enharmonically by adding a diminished 2nd to it or subtracting one from it.
| Degree | Cents | Standard notation | |
|---|---|---|---|
| Diatonic (5L 2s) interval names | Note names (on D) | ||
| 0 | 0 | Perfect unison (P1) | D |
| 1 | 100 | Augmented unison (A1) Minor second (m2) |
D# Eb |
| 2 | 200 | Major second (M2) Diminished third (d3) |
E Fb |
| 3 | 300 | Augmented second (A2) Minor third (m3) |
E# F |
| 4 | 400 | Major third (M3) Diminished fourth (d4) |
F# Gb |
| 5 | 500 | Perfect fourth (P4) | G |
| 6 | 600 | Augmented fourth (A4) Diminished fifth (d5) |
G# Ab |
| 7 | 700 | Perfect fifth (P5) | A |
| 8 | 800 | Augmented fifth (A5) Minor sixth (m6) |
A# Bb |
| 9 | 900 | Major sixth (M6) Diminished seventh (d7) |
B Cb |
| 10 | 1000 | Augmented sixth (A6) Minor seventh (m7) |
B# C |
| 11 | 1100 | Major seventh (M7) Diminished octave (d8) |
C# Db |
| 12 | 1200 | Perfect octave (P8) | D |
In 12edo:
- Ups and downs notation is identical to standard notation;
- Mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (♯) and flats (♭) for sagittal sharp (
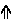 ) and sagittal flat (
) and sagittal flat (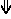 ) respectively.
) respectively.
Sagittal notation
This notation uses the same sagittal sequence as EDOs 5, 19, and 26, is a subset of the notations for EDOs 24, 36, 48, 60, 72, and 84, and is a superset of the notation for 6-EDO.
Evo flavor

Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
Revo flavor

Solfege
| Degree | Cents | Standard solfege (movable do) |
Uniform solfege (2-3 vowels) |
|---|---|---|---|
| 0 | 0 | Do | Da |
| 1 | 100 | Di (A1) Ra (m2) |
Du (A1) Fra (m2) |
| 2 | 200 | Re | Ra |
| 3 | 300 | Ri (A2) Me (m3) |
Ru (A2) Na (m3) |
| 4 | 400 | Mi | Ma (M3) Fo (d4) |
| 5 | 500 | Fa | Mu (A3) Fa (P4) |
| 6 | 600 | Fi (A4) Se (d5) |
Pa (A4) Sha (d5) |
| 7 | 700 | So | Sa |
| 8 | 800 | Si (A5) Le (m6) |
Su (A5) Fla (m6) |
| 9 | 900 | La | La (M6) Tho (d7) |
| 10 | 1000 | Li (A6) Te (m7) |
Lu (A6) Tha (m7) |
| 11 | 1100 | Ti | Ta (M7) Do (d8) |
| 12 | 1200 | Do | Da |
Approximation to JI

15-odd-limit interval mappings
The following tables show how 15-odd-limit intervals are represented in 12edo. Prime harmonics are in bold; inconsistent intervals are in italics.
Note that, since the cent was defined in terms of 12edo, the absolute and relative errors for 12edo are identical.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 3/2, 4/3 | 1.955 | 2.0 |
| 9/8, 16/9 | 3.910 | 3.9 |
| 13/11, 22/13 | 10.790 | 10.8 |
| 15/8, 16/15 | 11.731 | 11.7 |
| 5/4, 8/5 | 13.686 | 13.7 |
| 5/3, 6/5 | 15.641 | 15.6 |
| 7/5, 10/7 | 17.488 | 17.5 |
| 11/7, 14/11 | 17.508 | 17.5 |
| 9/5, 10/9 | 17.596 | 17.6 |
| 15/14, 28/15 | 19.443 | 19.4 |
| 13/7, 14/13 | 28.298 | 28.3 |
| 7/4, 8/7 | 31.174 | 31.2 |
| 7/6, 12/7 | 33.129 | 33.1 |
| 11/10, 20/11 | 34.996 | 35.0 |
| 9/7, 14/9 | 35.084 | 35.1 |
| 13/9, 18/13 | 36.618 | 36.6 |
| 15/11, 22/15 | 36.951 | 37.0 |
| 13/12, 24/13 | 38.573 | 38.6 |
| 13/8, 16/13 | 40.528 | 40.5 |
| 13/10, 20/13 | 45.786 | 45.8 |
| 11/9, 18/11 | 47.408 | 47.4 |
| 15/13, 26/15 | 47.741 | 47.7 |
| 11/8, 16/11 | 48.682 | 48.7 |
| 11/6, 12/11 | 49.363 | 49.4 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 3/2, 4/3 | 1.955 | 2.0 |
| 9/8, 16/9 | 3.910 | 3.9 |
| 15/8, 16/15 | 11.731 | 11.7 |
| 5/4, 8/5 | 13.686 | 13.7 |
| 5/3, 6/5 | 15.641 | 15.6 |
| 7/5, 10/7 | 17.488 | 17.5 |
| 11/7, 14/11 | 17.508 | 17.5 |
| 9/5, 10/9 | 17.596 | 17.6 |
| 15/14, 28/15 | 19.443 | 19.4 |
| 7/4, 8/7 | 31.174 | 31.2 |
| 7/6, 12/7 | 33.129 | 33.1 |
| 11/10, 20/11 | 34.996 | 35.0 |
| 9/7, 14/9 | 35.084 | 35.1 |
| 13/9, 18/13 | 36.618 | 36.6 |
| 15/11, 22/15 | 36.951 | 37.0 |
| 13/12, 24/13 | 38.573 | 38.6 |
| 13/8, 16/13 | 40.528 | 40.5 |
| 11/8, 16/11 | 48.682 | 48.7 |
| 11/6, 12/11 | 50.637 | 50.6 |
| 15/13, 26/15 | 52.259 | 52.3 |
| 11/9, 18/11 | 52.592 | 52.6 |
| 13/10, 20/13 | 54.214 | 54.2 |
| 13/7, 14/13 | 71.702 | 71.7 |
| 13/11, 22/13 | 89.210 | 89.2 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 3/2, 4/3 | 1.955 | 2.0 |
| 9/8, 16/9 | 3.910 | 3.9 |
| 13/11, 22/13 | 10.790 | 10.8 |
| 15/8, 16/15 | 11.731 | 11.7 |
| 5/4, 8/5 | 13.686 | 13.7 |
| 5/3, 6/5 | 15.641 | 15.6 |
| 7/5, 10/7 | 17.488 | 17.5 |
| 11/7, 14/11 | 17.508 | 17.5 |
| 9/5, 10/9 | 17.596 | 17.6 |
| 15/14, 28/15 | 19.443 | 19.4 |
| 13/7, 14/13 | 28.298 | 28.3 |
| 7/4, 8/7 | 31.174 | 31.2 |
| 7/6, 12/7 | 33.129 | 33.1 |
| 11/10, 20/11 | 34.996 | 35.0 |
| 9/7, 14/9 | 35.084 | 35.1 |
| 15/11, 22/15 | 36.951 | 37.0 |
| 13/10, 20/13 | 45.786 | 45.8 |
| 15/13, 26/15 | 47.741 | 47.7 |
| 11/8, 16/11 | 48.682 | 48.7 |
| 11/6, 12/11 | 50.637 | 50.6 |
| 11/9, 18/11 | 52.592 | 52.6 |
| 13/8, 16/13 | 59.472 | 59.5 |
| 13/12, 24/13 | 61.427 | 61.4 |
| 13/9, 18/13 | 63.382 | 63.4 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-19 12⟩ | [⟨12 19]] | +0.62 | 0.62 | 0.62 |
| 2.3.5 | 81/80, 128/125 | [⟨12 19 28]] | −1.56 | 3.11 | 3.11 |
| 2.3.5.7 | 36/35, 50/49, 64/63 | [⟨12 19 28 34]] | −3.95 | 4.92 | 4.94 |
| 2.3.5.7.17 | 36/35, 50/49, 51/49, 64/63 | [⟨12 19 28 34 49]] | −2.92 | 4.86 | 4.87 |
| 2.3.5.7.17.19 | 36/35, 50/49, 51/49, 57/56, 64/63 | [⟨12 19 28 34 49 51]] | −2.53 | 4.52 | 4.53 |
| 2.3.5.17 | 51/50, 81/80, 128/125 | [⟨12 19 28 49]] | −0.87 | 2.95 | 2.95 |
| 2.3.5.17.19 | 51/50, 76/75, 81/80, 128/125 | [⟨12 19 28 49 51]] | −0.81 | 2.64 | 2.64 |
- 12et (using the 12f val, where 9 steps is used as the approximation of 13/8 instead of 8 steps) is lower in relative error than any previous equal temperaments in the 3-, 5-, 7-, 11-, 13-, and 19-limit. The next equal temperaments doing better in those subgroups are 41, 19, 19, 22, 19/19e, and 19egh, respectively. 12et is even more prominent in the 2.3.5.7.17.19 subgroup, and the next equal temperament that does this better is 72.
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 11.7554 | 11.8436 | 12cde | ⟨12 19 27 33 41 44] |
| 11.8436 | 11.9329 | 12de | ⟨12 19 28 33 41 44] |
| 11.9329 | 11.9962 | 12e | ⟨12 19 28 34 41 44] |
| 11.9962 | 12.0256 | 12 | ⟨12 19 28 34 42 44] |
| 12.0256 | 12.2743 | 12f | ⟨12 19 28 34 42 45] |
Commas
12edo tempers out the following commas. This assumes val ⟨12 19 28 34 42 44].
| Prime limit |
Ratio[note 2] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | (12 digits) | [-19 12⟩ | 23.46 | Lalawa | Pythagorean comma |
| 5 | 648/625 | [3 4 -4⟩ | 62.57 | Quadgu | Diminished comma, greater diesis |
| 5 | (12 digits) | [18 -4 -5⟩ | 60.61 | Saquingu | Passion comma |
| 5 | 128/125 | [7 0 -3⟩ | 41.06 | Trigu | Augmented comma, lesser diesis |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic comma, Didymus' comma, meantone comma |
| 5 | 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma |
| 5 | (16 digits) | [26 -12 -3⟩ | 17.60 | Sasa-trigu | Misty comma |
| 5 | 32805/32768 | [-15 8 1⟩ | 1.95 | Layo | Schisma |
| 5 | (98 digits) | [161 -84 -12⟩ | 0.02 | Sepbisa-quadtrigu | Kirnberger's atom |
| 7 | 256/245 | [8 0 -1 -2⟩ | 76.03 | Rurugu | Bapbo comma |
| 7 | 59049/57344 | [-13 10 0 -1⟩ | 50.72 | Laru | Harrison's comma |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Mint comma, septimal quarter tone |
| 7 | 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Jubilisma |
| 7 | 3645/3584 | [-9 6 1 -1⟩ | 29.22 | Laruyo | Schismean comma |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma |
| 7 | 3125/3087 | [0 -2 5 -3⟩ | 21.18 | Triru-aquinyo | Gariboh comma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.79 | Zotrigu | Starling comma |
| 7 | 4000/3969 | [5 -4 3 -2⟩ | 13.47 | Rurutriyo | Octagar comma |
| 7 | (12 digits) | [-9 8 -4 2⟩ | 8.04 | Labizogugu | Varunisma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Ruyoyo | Marvel comma |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean comma |
| 7 | 5120/5103 | [10 -6 1 -1⟩ | 5.76 | Saruyo | Hemifamity comma |
| 7 | (16 digits) | [25 -14 0 -1⟩ | 3.80 | Sasaru | Garischisma |
| 7 | (12 digits) | [-11 2 7 -3⟩ | 1.63 | Latriru-asepyo | Metric comma |
| 7 | (12 digits) | [-4 6 -6 3⟩ | 0.33 | Trizogugu | Landscape comma |
| 11 | 128/121 | [7 0 0 0 -2⟩ | 97.36 | 1uu2 | Axirabian limma |
| 11 | 45/44 | [-2 2 1 0 -1⟩ | 38.91 | Luyo | Undecimal fifth tone |
| 11 | 56/55 | [3 0 -1 1 -1⟩ | 31.19 | Luzogu | Undecimal tritonic comma |
| 11 | 245/242 | [-1 0 1 2 -2⟩ | 21.33 | Luluzozoyo | Frostma |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.58 | Loruru | Mothwellsma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 896/891 | [7 -4 0 1 -1⟩ | 9.69 | Saluzo | Pentacircle comma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
| 11 | 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Bilorugu | Kalisma |
| 13 | 65/64 | [-6 0 1 0 0 1⟩ | 26.84 | Thoyo | Wilsorma |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap comma, biome comma |
| 13 | 144/143 | [4 2 0 0 -1 -1⟩ | 12.06 | Thulu | Grossma |
| 13 | 1001/1000 | [-3 0 -3 1 1 1⟩ | 1.73 | Tholozotrigu | Fairytale comma, sinbadma |
| 13 | 4096/4095 | [12 -2 -1 -1 0 -1⟩ | 0.42 | Sathurugu | Schismina |
| 17 | 51/50 | [-1 1 -2 0 0 0 1⟩ | 34.28 | Sogugu | Large septendecimal sixth tone |
| 17 | 52/51 | [2 -1 0 0 0 1 -1⟩ | 33.62 | Sutho | Small septendecimal sixth tone |
| 17 | 136/135 | [3 -3 -1 0 0 0 1⟩ | 12.78 | Sogu | Diatisma, fiventeen comma |
| 17 | 256/255 | [8 -1 -1 0 0 0 -1⟩ | 6.78 | Sugu | Charisma, septendecimal kleisma |
| 17 | 289/288 | [-5 -2 0 0 0 0 2⟩ | 6.00 | Soso | Semitonisma |
| 17 | 2601/2600 | [-3 2 -2 0 0 -1 2⟩ | 0.67 | Sosothugugu | Sextantonisma |
| 19 | 39/38 | [-1 1 0 0 0 1 0 -1⟩ | 44.97 | Nutho | Undevicesimal two-ninth tone |
| 19 | 96/95 | [5 1 -1 0 0 0 0 -1⟩ | 18.13 | Nugu | 19th-partial chroma |
| 19 | 153/152 | [-3 2 0 0 0 0 1 -1⟩ | 11.35 | Nuso | Ganassisma |
| 19 | 171/170 | [-1 2 -1 0 0 0 -1 1⟩ | 10.15 | Nosugu | Malcolmisma |
| 19 | 324/323 | [2 4 0 0 0 0 -1 -1⟩ | 5.35 | Nusu | Photisma |
| 19 | 361/360 | [-3 -2 -1 0 0 0 0 2⟩ | 4.80 | Nonogu | Go comma |
Rank-2 temperaments
- List of 12et rank two temperaments by badness
- List of 12et rank two temperaments by complexity
- List of edo-distinct 12f rank two temperaments
- Schismic–Pythagorean equivalence continuum
| Periods per 8ve |
Generator* | Pergen | Temperaments |
|---|---|---|---|
| 1 | 1\12 | (P8, P4/5) | Ripple / passion |
| 1 | 5\12 | (P8, P5) | Meantone / dominant |
| 2 | 5\12 (1\12) | (P8/2, P5) | Srutal / pajara / injera |
| 3 | 5\12 (1\12) | (P8/3, P5) | Augmented / lithium |
| 4 | 5\12 (1\12) | (P8/4, P5) | Diminished |
| 6 | 5\12 (1\12) | (P8/6, P5) | Hexe |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Octave stretch or compression
Whether there is intonational improvement from octave stretch and compression for 12edo varies by context. A slight compression such as what is given by 40ed10 and the zeta-optimized 99.81 ¢ step size shows improved intonation of harmonics 5 and 7 at the cost of worse 2 and 3, while stretching the octave for a purer 3 and for a better match of the inharmonicity on string instruments, like those in 7edf, 19edt, or 31ed6, also makes sense.
- Step size: 99.664 ¢, octave size: 1195.971 ¢
Compressing the octave of 12edo by 4 ¢ results in much improved primes 5, 7 and 11, but much worse primes 2 and 3. Both 7-limit WE and TE tuning do this. 40ed10 does this as well. An argument could be made that such tunings enable harmonies involving the 7th harmonic to regular old 12edo without even needing to add any new notes to the octave. This adds in brand new harmonic possibilities without breaking any common 12-tone music theory.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -4.0 | -8.3 | -8.1 | +4.3 | -12.4 | +19.8 | -12.1 | -16.7 | +0.3 | +34.6 | -16.4 |
| Relative (%) | -4.0 | -8.4 | -8.1 | +4.3 | -12.4 | +19.8 | -12.1 | -16.7 | +0.3 | +34.7 | -16.4 | |
| Step | 12 | 19 | 24 | 28 | 31 | 34 | 36 | 38 | 40 | 42 | 43 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +44.4 | +15.7 | -4.0 | -16.1 | -21.4 | -20.7 | -14.6 | -3.8 | +11.4 | +30.6 | -46.4 | -20.4 |
| Relative (%) | +44.5 | +15.8 | -4.1 | -16.2 | -21.5 | -20.8 | -14.7 | -3.8 | +11.5 | +30.7 | -46.6 | -20.5 | |
| Step | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 54 | 55 | |
- Step size: 99.807 ¢, octave size: 1197.686 ¢
Compressing the octave of 12edo by around 2 ¢ results in improved primes 5 and 7, but worse primes 2 and 3. The tuning 34zpi does this. It might be a good tuning for 5-limit meantone, for composers seeking more pure thirds and sixths than regular 12edo. It would be well suited for playing classic pieces written for historical temperaments, as well as being well suited to playing simultaneously with other instruments or voices that use just intonation.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.3 | -5.6 | -4.6 | +8.3 | -7.9 | +24.6 | -6.9 | -11.2 | +6.0 | +40.6 | -10.3 |
| Relative (%) | -2.3 | -5.6 | -4.6 | +8.3 | -8.0 | +24.7 | -7.0 | -11.3 | +6.0 | +40.7 | -10.3 | |
| Step | 12 | 19 | 24 | 28 | 31 | 34 | 36 | 38 | 40 | 42 | 43 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -49.0 | +22.3 | +2.7 | -9.3 | -14.4 | -13.6 | -7.4 | +3.7 | +19.0 | +38.3 | -38.7 | -12.6 |
| Relative (%) | -49.1 | +22.3 | +2.7 | -9.3 | -14.4 | -13.6 | -7.4 | +3.7 | +19.0 | +38.3 | -38.8 | -12.6 | |
| Step | 44 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 54 | 55 | |
- Step size: 99.868 ¢, octave size: 1198.416 ¢
Compressing the octave of 12edo by around 1 ¢ results in slightly improved primes 5 and 7, but slightly worse primes 2 and 3. Both 5-limit WE and TE tuning do this. This has the same benefits and drawbacks as 34zpi, but both are less intense here compared to 34zpi.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -1.6 | -4.5 | -3.2 | +10.0 | -6.0 | +26.7 | -4.8 | -8.9 | +8.4 | +43.1 | -7.6 |
| Relative (%) | -1.6 | -4.5 | -3.2 | +10.0 | -6.1 | +26.7 | -4.8 | -8.9 | +8.4 | +43.2 | -7.6 | |
| Step | 12 | 19 | 24 | 28 | 31 | 34 | 36 | 38 | 40 | 42 | 43 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -46.3 | +25.1 | +5.5 | -6.3 | -11.4 | -10.5 | -4.2 | +6.8 | +22.2 | +41.6 | -35.4 | -9.2 |
| Relative (%) | -46.4 | +25.1 | +5.5 | -6.3 | -11.4 | -10.5 | -4.2 | +6.8 | +22.3 | +41.6 | -35.4 | -9.2 | |
| Step | 44 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 54 | 55 | |
- 12edo
- Step size: 100.000 ¢, octave size: 1200.000 ¢
Pure-octaves 12edo performs well on harmonics 2, 3 and 5 but poorly on harmonics 7, 11 and 13 compared to other edos with a similar number of notes per octave.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -2.0 | +0.0 | +13.7 | -2.0 | +31.2 | +0.0 | -3.9 | +13.7 | +48.7 | -2.0 |
| Relative (%) | +0.0 | -2.0 | +0.0 | +13.7 | -2.0 | +31.2 | +0.0 | -3.9 | +13.7 | +48.7 | -2.0 | |
| Steps (reduced) |
12 (0) |
19 (7) |
24 (0) |
28 (4) |
31 (7) |
34 (10) |
36 (0) |
38 (2) |
40 (4) |
42 (6) |
43 (7) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -40.5 | +31.2 | +11.7 | +0.0 | -5.0 | -3.9 | +2.5 | +13.7 | +29.2 | +48.7 | -28.3 | -2.0 |
| Relative (%) | -40.5 | +31.2 | +11.7 | +0.0 | -5.0 | -3.9 | +2.5 | +13.7 | +29.2 | +48.7 | -28.3 | -2.0 | |
| Steps (reduced) |
44 (8) |
46 (10) |
47 (11) |
48 (0) |
49 (1) |
50 (2) |
51 (3) |
52 (4) |
53 (5) |
54 (6) |
54 (6) |
55 (7) | |
- Step size: 100.063 ¢, octave size: 1200.757 ¢
Stretching the octave of 12edo by a little less than 1 ¢ results in an improved prime 3, but worse primes 2, 5, and 7. This loosely resembles the stretched-octave tunings commonly used on pianos. It may better match the slightly inharmonic partials of some string instruments. The tuning 31ed6 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.8 | -0.8 | +1.5 | +15.5 | +0.0 | +33.3 | +2.3 | -1.5 | +16.2 | -48.7 | +0.8 |
| Relative (%) | +0.8 | -0.8 | +1.5 | +15.4 | +0.0 | +33.3 | +2.3 | -1.5 | +16.2 | -48.7 | +0.8 | |
| Steps (reduced) |
12 (12) |
19 (19) |
24 (24) |
28 (28) |
31 (0) |
34 (3) |
36 (5) |
38 (7) |
40 (9) |
41 (10) |
43 (12) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -37.8 | +34.1 | +14.7 | +3.0 | -1.9 | -0.8 | +5.7 | +17.0 | +32.6 | -48.0 | -24.9 | +1.5 |
| Relative (%) | -37.7 | +34.1 | +14.7 | +3.0 | -1.9 | -0.8 | +5.7 | +17.0 | +32.5 | -47.9 | -24.9 | +1.5 | |
| Steps (reduced) |
44 (13) |
46 (15) |
47 (16) |
48 (17) |
49 (18) |
50 (19) |
51 (20) |
52 (21) |
53 (22) |
53 (22) |
54 (23) |
55 (24) | |
- Step size: 101.103 ¢, octave size: 1201.235 ¢
Stretching the octave of 12edo by a little more than 1 ¢ results in an improved prime 3, but worse primes 2, 5, and 7. It may better match the slightly inharmonic partials of some string instruments. The tuning 19edt does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.2 | +0.0 | +2.5 | +16.6 | +1.2 | +34.7 | +3.7 | +0.0 | +17.8 | -47.1 | +2.5 |
| Relative (%) | +1.2 | +0.0 | +2.5 | +16.6 | +1.2 | +34.6 | +3.7 | +0.0 | +17.8 | -47.1 | +2.5 | |
| Steps (reduced) |
12 (12) |
19 (0) |
24 (5) |
28 (9) |
31 (12) |
34 (15) |
36 (17) |
38 (0) |
40 (2) |
41 (3) |
43 (5) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -36.0 | +35.9 | +16.6 | +4.9 | +0.1 | +1.2 | +7.7 | +19.0 | +34.7 | -45.9 | -22.7 | +3.7 |
| Relative (%) | -36.0 | +35.9 | +16.6 | +4.9 | +0.1 | +1.2 | +7.7 | +19.0 | +34.6 | -45.8 | -22.7 | +3.7 | |
| Steps (reduced) |
44 (6) |
46 (8) |
47 (9) |
48 (10) |
49 (11) |
50 (12) |
51 (13) |
52 (14) |
53 (15) |
53 (15) |
54 (16) |
55 (17) | |
- Step size: 100.279 ¢, octave size: 1203.351 ¢
Stretching the octave of 12edo by around 3 ¢ results in improved primes 3 and 13, but much worse primes 2, 5, and 7. This has similar benefits and drawbacks to Pythagorean tuning. Most modern music probably will not sound very good here because of the off 5th harmonic. The tuning 7edf does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.4 | +3.4 | +6.7 | +21.5 | +6.7 | +40.7 | +10.1 | +6.7 | +24.9 | -39.9 | +10.1 |
| Relative (%) | +3.3 | +3.3 | +6.7 | +21.4 | +6.7 | +40.6 | +10.0 | +6.7 | +24.8 | -39.8 | +10.0 | |
| Steps (reduced) |
12 (5) |
19 (5) |
24 (3) |
28 (0) |
31 (3) |
34 (6) |
36 (1) |
38 (3) |
40 (5) |
41 (6) |
43 (1) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -28.2 | +44.0 | +24.9 | +13.4 | +8.7 | +10.1 | +16.7 | +28.2 | +44.0 | -36.5 | -13.2 | +13.4 |
| Relative (%) | -28.2 | +43.9 | +24.8 | +13.4 | +8.7 | +10.0 | +16.7 | +28.1 | +43.9 | -36.4 | -13.2 | +13.4 | |
| Steps (reduced) |
44 (2) |
46 (4) |
47 (5) |
48 (6) |
49 (0) |
50 (1) |
51 (2) |
52 (3) |
53 (4) |
53 (4) |
54 (5) |
55 (6) | |
Scales
The two most common 12edo mos scales are meantone[5] and meantone[7].
- Diatonic (meantone) 5L2s 2221221 (generator = 7\12)
- Pentatonic (meantone) 2L3s 22323 (generator = 7\12)
- Diminished 4L4s 12121212 (generator = 1\12, period = 3\12)
Non-mos scales
Due to 12edo's dominance, some non-mos scales are also widely used in many musical practices around the world.
- Harmonic major – 2212132
- Melodic major – 2212122
- Hungarian minor – 2131131
- Maqam hijaz / double harmonic major – 1312131
- 5-odd-limit tonality diamond – 3112113
Well temperaments
- For a list of historical well temperaments, see Well temperament.
Music
- See also: Category:12edo tracks
See also
- Lumatone mapping for 12edo
- purdal:12-EDD[dead link]
- Near12 – a just intonation scale where every interval is within 12.5 cents of a 12edo step