26edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Francium (talk | contribs)
4,621 edits
Sintel (talk | contribs)
autopatrolled
1,547 edits
→Approximation to JI: -zeta peak index
 
(37 intermediate revisions by 14 users not shown)
Line 6: Line 6:
}}
}}
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|26}}
{{ED intro}}


== Theory ==
== Theory ==
26edo tempers out [[81/80]] in the [[5-limit]], making it a [[meantone]] tuning with a very flat fifth.  
26edo has a [[3/2|perfect fifth]] of about 692 cents and [[tempering out|tempers out]] [[81/80]] in the [[5-limit]], making it a very flat [[meantone]] tuning (0.088957{{c}} flat of the [[4/9-comma meantone]] fifth) with a very soft [[5L 2s|diatonic scale]].  


In the [[7-limit]], it tempers out 50/49, 525/512 and 875/864, and [[support]]s temperaments like [[injera]], [[flattone]], [[lemba]] and [[doublewide]]. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the [[13-odd-limit]] [[consistent]]ly. 26edo has a very good approximation of the harmonic seventh ([[7/4]]), as it is the denominator of a convergent to log<sub>2</sub>7.
In the [[7-limit]], it tempers out [[50/49]], [[525/512]], and [[875/864]], and [[support]]s temperaments like [[injera]], [[flattone]], [[lemba]], and [[doublewide]]. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the [[13-odd-limit]] [[consistent]]ly. 26edo has a very good approximation of the harmonic seventh ([[7/4]]), as it is the denominator of a convergent to log<sub>2</sub>7.


26edo's minor sixth (1.6158) is very close to ''φ'' ≈ 1.6180 (i.e. the golden ratio).
26edo's minor sixth (1.6158) is very close to {{nowrap|''φ'' ≈ 1.6180}} (i.e. the golden ratio).


With a fifth of 15 steps, it can be equally divided into 3 or 5, supporting [[slendric]] temperament and [[bleu]] temperament respectively.
With a fifth of 15 steps, it can be equally divided into 3 or 5, supporting [[slendric]] temperament and [[bleu]] temperament respectively.
Line 19: Line 19:
The structure of 26edo is an interesting beast, with various approaches relating it to various rank-2 temperaments.
The structure of 26edo is an interesting beast, with various approaches relating it to various rank-2 temperaments.


# In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which yields interesting but to some unsatisfying results (due mainly to the dissonance of its thirds, and its major second of approximately [[10/9]] instead of [[9/8]]).
# In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which provides an interesting structure but unsatisfying intonation due mainly to the poorly tuned thirds. Extending meantone harmony to the 7-limit is quite intuitive; for example, augmented becomes supermajor, and diminished becomes subminor. Simple mappings for harmonics up to 13 are also achieved.
# As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, [[38edo]]) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&amp;26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of [[14edo]].
# As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, [[38edo]]) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&amp;26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of [[14edo]].
# 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas [[65536/65219]] and {{monzo| -3 0 0 6 -4 }}. The 65536/65219 comma, the orgonisma, leads to the [[Orgonia|orgone temperament]] with an approximate 77/64 generator of 7\26, with mos scales of size 7, 11 and 15. The {{monzo| -3 0 0 6 -4 }} comma leads to a half-octave period and an approximate [[49/44]] generator of 4\26, leading to mos of size 8 and 14.
# 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas [[65536/65219]] and {{monzo| -3 0 0 6 -4 }}. The 65536/65219 comma, the orgonisma, leads to the [[Orgonia|orgone temperament]] with an approximate 77/64 generator of 7\26, with mos scales of size 7, 11 and 15. The {{monzo| -3 0 0 6 -4 }} comma leads to a half-octave period and an approximate [[49/44]] generator of 4\26, leading to mos of size 8 and 14.
# We can also treat 26edo as a full 13-limit temperament, since it is consistent on the 13-odd-limit (unlike all lower edos).
# We can also treat 26edo as a full 13-limit temperament, since it is consistent on the 13-odd-limit (unlike all lower edos).
# It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fifths gives a 17:14 and four gives a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and [[33edo]] even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.
# It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fourths give a 17:14 and four fifths give a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and [[33edo]] even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.


Its step, as well as the octave-inverted and octave-equivalent versions of it, holds the distinction for having around the highest [[harmonic entropy]] possible and thus is, in theory, most dissonant, assuming the relatively common values of ''a'' = 2 and ''s'' = 1.01. This property is shared with all edos between around 20 and 30. Intervals smaller than this tend to be perceived as unison and are more consonant as a result; intervals larger than this have less "tension" and thus are also more consonant.
Its step of 46.2{{c}}, as well as the octave-inverted and octave-equivalent versions of it, holds the distinction for having around the highest [[harmonic entropy]] possible. In other words, there is a common perception of quartertones as being the most dissonant intervals. This property is shared with all edos between around 20 and 30. Intervals smaller than this tend to be perceived as unison and are more consonant as a result; intervals larger than this have less "tension" and thus are also more consonant.
 
Thanks to its sevenths, 26edo is an ideal tuning for its size for [[metallic harmony]].


=== Odd harmonics ===
=== Odd harmonics ===
{{Harmonics in equal|26}}
{{Harmonics in equal|26}}
=== Subsets and supersets ===
26edo has [[2edo]] and [[13edo]] as subsets, of which 13edo is non-trivial, sharing harmonics 5 and 9 through 23 (including direct approximations) with 26edo. Multiplying 26edo by 3 yields [[78edo]], which corrects several harmonics.


== Intervals ==
== Intervals ==
Line 35: Line 40:
! Degrees
! Degrees
! [[Cent]]s
! [[Cent]]s
! Approximate Ratios*
! Approximate ratios<ref group="note">{{sg|limit=13-limit}}</ref>
! Interval<br>Name
! Interval<br>name
! Example<br>in D
! [[SKULO interval names|SKULO]]<br>[[SKULO interval names|Interval name]]
! Example<br>in D
! Example<br>in D
![[SKULO interval names|SKULO]]
! colspan="2" | [[Solfege|Solfeges]]
[[SKULO interval names|Interval Name]]
!Example
in D
! colspan="2" |[[Solfege|Solfeges]]
|-
|-
| 0
| 0
Line 49: Line 52:
| P1
| P1
| D
| D
|P1
| P1
|D
| D
| da
| da
| do
| do
Line 59: Line 62:
| A1
| A1
| D#
| D#
|A1, S1
| A1, S1
|D#, SD
| D#, SD
| du
| du
| di
| di
Line 69: Line 72:
| d2
| d2
| Ebb
| Ebb
|sm2
| sm2
|sEb
| sEb
| fro
| fro
| rih
| rih
Line 79: Line 82:
| m2
| m2
| Eb
| Eb
|m2
| m2
|Eb
| Eb
| fra
| fra
| ru
| ru
Line 89: Line 92:
| M2
| M2
| E
| E
|M2
| M2
|E
| E
| ra
| ra
| re
| re
Line 99: Line 102:
| A2
| A2
| E#
| E#
|SM2
| SM2
|SE
| SE
| ru
| ru
| ri
| ri
Line 109: Line 112:
| d3
| d3
| Fb
| Fb
|sm3
| sm3
|sF
| sF
| no
| no
| ma
| ma
Line 119: Line 122:
| m3
| m3
| F
| F
|m3
| m3
|F
| F
| na
| na
| me
| me
Line 129: Line 132:
| M3
| M3
| F#
| F#
|M3
| M3
|F#
| F#
| ma
| ma
| muh/mi
| muh/mi
Line 139: Line 142:
| A3
| A3
| Fx
| Fx
|SM3
| SM3
|SF#
| SF#
| mu
| mu
| maa
| maa
Line 149: Line 152:
| d4
| d4
| Gb
| Gb
|s4
| s4
|sG
| sG
| fo
| fo
| fe
| fe
Line 159: Line 162:
| P4
| P4
| G
| G
|P4
| P4
|G
| G
| fa
| fa
| fa
| fa
Line 169: Line 172:
| A4
| A4
| G#
| G#
|A4
| A4
|G#
| G#
| fu/pa
| fu/pa
| fu
| fu
Line 179: Line 182:
| AA4, dd5
| AA4, dd5
| Gx, Abb
| Gx, Abb
|SA4, sd5
| SA4, sd5
|SG#, sAb
| SG#, sAb
| pu/sho
| pu/sho
| fi/se
| fi/se
Line 189: Line 192:
| d5
| d5
| Ab
| Ab
|d5
| d5
|Ab
| Ab
| sha/so
| sha/so
| su
| su
Line 199: Line 202:
| P5
| P5
| A
| A
|P5
| P5
|A
| A
| sa
| sa
| sol
| sol
Line 209: Line 212:
| A5
| A5
| A#
| A#
|S5
| S5
|SA
| SA
| su
| su
| si
| si
Line 219: Line 222:
| d6
| d6
| Bbb
| Bbb
|sm6
| sm6
|sBb
| sBb
| flo
| flo
| leh
| leh
Line 229: Line 232:
| m6
| m6
| Bb
| Bb
|m6
| m6
|Bb
| Bb
| fla
| fla
| le/lu
| le/lu
Line 239: Line 242:
| M6
| M6
| B
| B
|M6
| M6
|B
| B
| la
| la
| la
| la
Line 249: Line 252:
| A6
| A6
| B#
| B#
|SM6
| SM6
|SB
| SB
| lu
| lu
| li
| li
Line 259: Line 262:
| d7
| d7
| Cb
| Cb
|sm7
| sm7
|sC
| sC
| tho
| tho
| ta
| ta
Line 269: Line 272:
| m7
| m7
| C
| C
|m7
| m7
|C
| C
| tha
| tha
| te
| te
Line 279: Line 282:
| M7
| M7
| C#
| C#
|M7
| M7
|C#
| C#
| ta
| ta
| tu/ti
| tu/ti
Line 289: Line 292:
| A7
| A7
| Cx
| Cx
|SM7
| SM7
|SC#
| SC#
| tu
| tu
| to
| to
Line 299: Line 302:
| d8
| d8
| Db
| Db
|d8, s8
| d8, s8
|Db, sD
| Db, sD
| do
| do
| da
| da
Line 309: Line 312:
| P8
| P8
| D
| D
|P8
| P8
|D
| D
| da
| da
| do
| do
|}
|}
* based on treating 26edo as a [[13-limit]] temperament; other approaches are possible.


=== Interval quality and chord names in color notation ===
=== Interval quality and chord names in color notation ===
Line 363: Line 365:
! [[Kite's color notation|Color of the 3rd]]
! [[Kite's color notation|Color of the 3rd]]
! JI chord
! JI chord
! Notes as Edoteps
! Notes as Edosteps
! Notes of C Chord
! Notes of C Chord
! Written Name
! Written Name
Line 398: Line 400:


For a more complete list, see [[Ups and downs notation #Chord names in other EDOs]].
For a more complete list, see [[Ups and downs notation #Chord names in other EDOs]].
== Notation ==
=== Sagittal notation ===
This notation uses the same sagittal sequence as EDOs [[5edo#Sagittal notation|5]], [[12edo#Sagittal notation|12]], and [[19edo#Sagittal notation|19]], is a subset of the notation for [[52edo#Sagittal notation|52-EDO]], and is a superset of the notation for [[13edo#Sagittal notation|13-EDO]].
==== Evo flavor ====
<imagemap>
File:26-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 463 0 623 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
default [[File:26-EDO_Evo_Sagittal.svg]]
</imagemap>
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
==== Revo flavor ====
<imagemap>
File:26-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 511 0 671 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
default [[File:26-EDO_Revo_Sagittal.svg]]
</imagemap>


== Approximation to JI ==
== Approximation to JI ==
Line 404: Line 430:


== Approximation to irrational intervals ==
== Approximation to irrational intervals ==
After [[13edo #Approximation to irrational intervals|13edo]], the weird coïncidences continue: [[11/7 #Proximity with π/2|acoustic π/2]] (17\26) is just in between the ϕ intervals provided by 13edo (16\26 for [[Logarithmic phi|logarithmic ϕ]]/2, and 18\26 for [[Acoustic phi|acoustic ϕ]]).
26edo approximates both [[acoustic phi]] (the [[golden ratio]]) and [[pi]] quite accurately. Not until 1076edo do we find a better edo in terms of relative error on these intervals.
 
Not until 1076edo do we find a better edo in terms of relative error on these intervals (which is not a very relevant edo for logarithmic ϕ, since 1076 does not belong to the Fibonacci sequence).
 
However, it should be noted that [[User:Contribution/Logarithmic constants VS acoustic constants (opinion piece article)|from an acoustic perspective]], acoustic π and acoustic ϕ are both better represented on [[23edo]].


{| class="wikitable center-all"
{| class="wikitable center-all"
|+ Direct approximation
|+ style="font-size: 105%;" | Direct approximation
|-
|-
! Interval
! Interval
Line 436: Line 458:


== Regular temperament properties ==
== Regular temperament properties ==
{| class="wikitable"
{| class="wikitable center-4 center-5 center-6"
! rowspan="2" | [[Just intonation subgroup|Subgroup]]
|-
! rowspan="2" | [[Comma basis|Comma List]]
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma basis]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve Stretch (¢)
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning Error
! colspan="2" | Tuning error
|-
|-
! [[TE error|Absolute]] (¢)
! [[TE error|Absolute]] (¢)
Line 447: Line 470:
|-
|-
| 2.3
| 2.3
| [-41 26⟩
| {{monzo| -41 26 }}
| [⟨26 41]]
| {{mapping| 26 41 }}
| +3.043
| +3.043
| 3.05
| 3.05
Line 455: Line 478:
| 2.3.5
| 2.3.5
| 81/80, 78125/73728
| 81/80, 78125/73728
| [⟨26 41 60]]
| {{mapping| 26 41 60 }}
| +4.489
| +4.489
| 3.22
| 3.22
Line 462: Line 485:
| 2.3.5.7
| 2.3.5.7
| 50/49, 81/80, 405/392
| 50/49, 81/80, 405/392
| [⟨26 41 60 73]]
| {{mapping| 26 41 60 73 }}
| +3.324
| +3.324
| 3.44
| 3.44
Line 469: Line 492:
| 2.3.5.7.11
| 2.3.5.7.11
| 45/44, 50/49, 81/80, 99/98
| 45/44, 50/49, 81/80, 99/98
| [⟨26 41 60 73 90]]
| {{mapping| 26 41 60 73 90 }}
| +2.509
| +2.509
| 3.48
| 3.48
Line 476: Line 499:
| 2.3.5.7.11.13
| 2.3.5.7.11.13
| 45/44, 50/49, 65/64, 78/77, 81/80
| 45/44, 50/49, 65/64, 78/77, 81/80
| [⟨26 41 60 73 90 96]]
| {{mapping| 26 41 60 73 90 96 }}
| +2.531
| +2.531
| 3.17
| 3.17
Line 483: Line 506:
| 2.3.5.7.11.13.17
| 2.3.5.7.11.13.17
| 45/44, 50/49, 65/64 78/77, 81/80, 85/84
| 45/44, 50/49, 65/64 78/77, 81/80, 85/84
| [⟨26 41 60 73 90 96 106]]
| {{mapping| 26 41 60 73 90 96 106 }}
| +2.613
| +2.613
| 2.94
| 2.94
Line 490: Line 513:
| 2.3.5.7.11.13.17.19
| 2.3.5.7.11.13.17.19
| 45/44, 50/49, 57/56, 65/64, 78/77, 81/80, 85/84
| 45/44, 50/49, 57/56, 65/64, 78/77, 81/80, 85/84
| [⟨26 41 60 73 90 96 106 110]]
| {{mapping| 26 41 60 73 90 96 106 110 }}
| +2.894
| +2.894
| 2.85
| 2.85
| 6.18
| 6.18
|}
|}
26et is lower in relative error than any previous equal temperaments in the [[17-limit|17-]], [[19-limit|19-]], [[23-limit|23-]], and [[29-limit]] (using the 26i val for the 23- and 29-limit). The next equal temperaments performing better in those subgroups are [[27edo|27eg]], 27eg, [[29edo|29g]], and [[46edo|46]], respectively.  
* 26et is lower in relative error than any previous equal temperaments in the [[17-limit|17-]], [[19-limit|19-]], [[23-limit|23-]], and [[29-limit]] (using the 26i val for the 23- and 29-limit). The next equal temperaments performing better in those subgroups are [[27edo|27eg]], 27eg, [[29edo|29g]], and [[46edo|46]], respectively.  


=== Rank-2 Temperaments ===
=== Rank-2 Temperaments ===
* [[List of 26et rank two temperaments by badness]]
* [[List of 26et rank two temperaments by badness]]
* [[List of edo-distinct 26et rank two temperaments]]
* [[List of edo-distinct 26et rank two temperaments]]
Important MOSes include (in addition to ones found in [[13edo]]):


* diatonic ([[flattone]]) 4443443 (15\26, 1\1)
Important mos scales include (in addition to ones found in [[13edo]]):
* chromatic ([[flattone]]) 313131331313 (15\26, 1\1)
* [[Flattone]][7] (diatonic) 4443443 (15\26, 1\1)
* enharmonic ([[flattone]]) 2112112112121121121 (15\26, 1\1)
* [[Flattone]][12] (chromatic) 313131331313 (15\26, 1\1)
* [[orgone]] 5525252 (7\26, 1\1)
* [[Flattone]][19] (enharmonic) 2112112112121121121 (15\26, 1\1)
* [[orgone]] 32322322322 (7\26, 1\1)
* [[Orgone]][7] 5525252 (7\26, 1\1)
* [[orgone]] 212212221222122 (7\26, 1\1)
* [[Orgone]][11] 32322322322 (7\26, 1\1)
* [[lemba]] 553553 (5\26, 1\2)
* [[Orgone]][15] 212212221222122 (7\26, 1\1)
* [[lemba]] 3232332323 (5\26, 1\2)
* [[Lemba]][6] 553553 (5\26, 1\2)
* [[lemba]] 2122122121221221 (5\26, 1\2)
* [[Lemba]][10] 3232332323 (5\26, 1\2)
* [[Lemba]][16] 2122122121221221 (5\26, 1\2)


{| class="wikitable center-all left-3"
{| class="wikitable center-all left-3"
|-
|-
! Periods<br>per octave
! Periods<br>per 8ve
! Generator
! Generator
! Temperaments
! Temperaments
Line 520: Line 543:
| 1
| 1
| 1\26
| 1\26
| [[Quartonic]]/[[Quarto]]
| [[Quartonic]] / [[quarto]]
|-
|-
| 1
| 1
| 3\26
| 3\26
| [[Jerome]]/[[Chromatic_pairs|Bleu]]/[[Secund]]/[[Glacier]]
| [[Glacier]] / [[bleu]] / [[jerome]] / [[secund]]
|-
|-
| 1
| 1
| 5\26
| 5\26
| [[Cynder]]/[[Mothra]]
| [[Cynder]] / [[mothra]]
|-
|-
| 1
| 1
| 7\26
| 7\26
| [[Superkleismic]]/[[Orgone]]/[[Shibboleth]]
| [[Orgone]] / [[superkleismic]]
|-
|-
| 1
| 1
| 9\26
| 9\26
| [[Roman]]/[[Wesley]]
| [[Wesley]] / [[roman]]
|-
|-
| 1
| 1
| 11\26
| 11\26
| [[Meantone]]/[[Flattone]]
| [[Flattone]] / [[flattertone]]
|-
|-
| 2
| 2
Line 552: Line 575:
| 2
| 2
| 3\26
| 3\26
| [[Fifive]]/[[Crepuscular]]
| [[Fifive]] / [[crepuscular]]
|-
|-
| 2
| 2
| 4\26
| 4\26
| [[Unidec]]/[[Gamelismic_clan#Unidec-Hendec|Hendec]]/[[Dubbla]]
| [[Dubbla]]<br>[[Unidec]] / [[hendec]]
|-
|-
| 2
| 2
| 5\26
| 5\26
| | [[Lemba]]
| [[Lemba]]
|-
|-
| 2
| 2
| 6\26
| 6\26
| [[Doublewide]]/[[Cavalier]]
| [[Doublewide]] / [[cavalier]]
|-
|-
| 13
| 13
Line 572: Line 595:


=== Hendec in 26et ===
=== Hendec in 26et ===
[[Gamelismic_clan#Unidec-Hendec|Hendec]], the 13-limit 26&amp;46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.
[[Hendec]], the 13-limit {{nowrap|26 & 46}} temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.


=== Commas ===
=== Commas ===
26et [[tempers out]] the following [[commas]]. (Note: This assumes the [[val]] {{val| 26 41 60 73 90 96 }}.)
26et [[tempering out|tempers out]] the following [[commas]]. This assumes the [[val]] {{val| 26 41 60 73 90 96 }}.


{| class="commatable wikitable center-all left-3 right-4 left-6"
{| class="commatable wikitable center-all left-3 right-4 left-6"
|-
|-
! [[Harmonic limit|Prime<br>Limit]]
! [[Harmonic limit|Prime<br>limit]]
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Ratio]]<ref group="note">{{rd}}</ref>
! [[Monzo]]
! [[Monzo]]
! [[Cents]]
! [[Cents]]
Line 598: Line 621:
| 0.23
| 0.23
| Quadla-sepquingu
| Quadla-sepquingu
| [[Senior]]
| [[Senior comma]]
|-
|-
| 7
| 7
Line 612: Line 635:
| 34.98
| 34.98
| Biruyo
| Biruyo
| Tritonic diesis, Jubilisma
| Jubilisma, tritonic diesis
|-
|-
| 7
| 7
Line 626: Line 649:
| 13.47
| 13.47
| Sarurutriyo
| Sarurutriyo
| Octagar
| Octagar comma
|-
|-
| 7
| 7
Line 633: Line 656:
| 13.07
| 13.07
| Triru-agu
| Triru-agu
| Orwellisma, Orwell comma
| Orwellisma
|-
|-
| 7
| 7
Line 717: Line 740:
| 16.57
| 16.57
| Thuzoyo
| Thuzoyo
| Animist
| Animist comma
|}
|}
<references/>


== Scales ==
== Scales ==
Line 741: Line 763:


-Igs
-Igs
=== MOS scales ===
''See [[List of MOS scales in 26edo]]''


== Instruments ==
== Instruments ==
Line 746: Line 771:
[[File:12072608 10207851395433055 404343132969239728 n.jpg|none|thumb|960x960px]]
[[File:12072608 10207851395433055 404343132969239728 n.jpg|none|thumb|960x960px]]


* [[Lumatone mapping for 26edo]]
== Literature ==
== Literature ==
[http://www.ronsword.com Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.]
[http://www.ronsword.com Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.]
Line 764: Line 790:
; [[Abnormality]]
; [[Abnormality]]
* [https://www.youtube.com/watch?v=Tl-AN2zQeAI ''Break''] (2024)
* [https://www.youtube.com/watch?v=Tl-AN2zQeAI ''Break''] (2024)
* [https://www.youtube.com/watch?v=f5eYIH3TO4o ''Moondust''] (2024)


; [[Jim Aikin]]
; [[Jim Aikin]]
Line 770: Line 797:
; [[Beheld]]
; [[Beheld]]
* [https://www.youtube.com/watch?v=0WbLTtDZUms ''Damp vibe''] (2022)
* [https://www.youtube.com/watch?v=0WbLTtDZUms ''Damp vibe''] (2022)
; [[benyamind]]
* [https://www.youtube.com/watch?v=H1hYI2hBcEU ''Cinematic music in 26-tone equal temperament''] (2024)


; [[Cameron Bobro]]
; [[Cameron Bobro]]
* [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Bobro/LittleFugueIn26_CBobro.mp3 Little Fugue in 26]{{dead link}}
* [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Bobro/LittleFugueIn26_CBobro.mp3 Little Fugue in 26]{{dead link}}
; [[User:CellularAutomaton|CellularAutomaton]]
* [https://cellularautomaton.bandcamp.com/track/innerstate ''Innerstate''] (2024)


; [[City of the Asleep]]
; [[City of the Asleep]]
Line 780: Line 813:
; [[Zach Curley]]
; [[Zach Curley]]
* [http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Guitar%20Serenade%20in%20Q%20Major.mp3 Guitar Serenade in Q Major]{{dead link}}
* [http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Guitar%20Serenade%20in%20Q%20Major.mp3 Guitar Serenade in Q Major]{{dead link}}
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/FxTxQ0ayDpg ''Microtonal Improvisation in 26edo''] (2023)


; [[User:Eboone|Ebooone]]
; [[User:Eboone|Ebooone]]
Line 803: Line 839:
* [https://www.youtube.com/watch?v=r0jCdHEZpzM Claudi Meneghin - Suite (Prelude, Variations, Fugue) in 26edo, for Synth & Baroque Bassoon] (2023)
* [https://www.youtube.com/watch?v=r0jCdHEZpzM Claudi Meneghin - Suite (Prelude, Variations, Fugue) in 26edo, for Synth & Baroque Bassoon] (2023)
* [https://www.youtube.com/watch?v=rjo3X1-D57Y Canon 3-in-1 on a Ground for Baroque Ensemble] (2023)
* [https://www.youtube.com/watch?v=rjo3X1-D57Y Canon 3-in-1 on a Ground for Baroque Ensemble] (2023)
; [[Microtonal Maverick]] (formerly The Xen Zone)
* [https://www.youtube.com/watch?v=qm_k9xjXRf0 ''The Microtonal Magic of 26EDO (with 13-limit jam)''] (2024)
* [https://www.youtube.com/watch?v=im2097HVqgA ''The Blues but with 26 Notes per Octave''] (2024) (explanatory video &mdash; contiguous music starts at 08:48)


; [[Herman Miller]]
; [[Herman Miller]]
Line 839: Line 879:
* [http://micro.soonlabel.com/26edo/20161224_26edo_wing.mp3 ''Morpheous Wing'' in 26 edo] (2016)
* [http://micro.soonlabel.com/26edo/20161224_26edo_wing.mp3 ''Morpheous Wing'' in 26 edo] (2016)


== See also ==
== Notes ==
* [[Lumatone mapping for 26edo]]
<references group="note" />


[[Category:Listen]]
[[Category:Listen]]

Latest revision as of 00:00, 16 August 2025

← 25edo 26edo 27edo →
Prime factorization 2 × 13
Step size 46.1538 ¢ 
Fifth 15\26 (692.308 ¢)
Semitones (A1:m2) 1:3 (46.15 ¢ : 138.5 ¢)
Consistency limit 13
Distinct consistency limit 5

26 equal divisions of the octave (abbreviated 26edo or 26ed2), also called 26-tone equal temperament (26tet) or 26 equal temperament (26et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 26 equal parts of about 46.2 ¢ each. Each step represents a frequency ratio of 21/26, or the 26th root of 2.

Theory

26edo has a perfect fifth of about 692 cents and tempers out 81/80 in the 5-limit, making it a very flat meantone tuning (0.088957 ¢ flat of the 4/9-comma meantone fifth) with a very soft diatonic scale.

In the 7-limit, it tempers out 50/49, 525/512, and 875/864, and supports temperaments like injera, flattone, lemba, and doublewide. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the 13-odd-limit consistently. 26edo has a very good approximation of the harmonic seventh (7/4), as it is the denominator of a convergent to log27.

26edo's minor sixth (1.6158) is very close to φ ≈ 1.6180 (i.e. the golden ratio).

With a fifth of 15 steps, it can be equally divided into 3 or 5, supporting slendric temperament and bleu temperament respectively.

The structure of 26edo is an interesting beast, with various approaches relating it to various rank-2 temperaments.

  1. In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which provides an interesting structure but unsatisfying intonation due mainly to the poorly tuned thirds. Extending meantone harmony to the 7-limit is quite intuitive; for example, augmented becomes supermajor, and diminished becomes subminor. Simple mappings for harmonics up to 13 are also achieved.
  2. As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, 38edo) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of 14edo.
  3. 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas 65536/65219 and [-3 0 0 6 -4⟩. The 65536/65219 comma, the orgonisma, leads to the orgone temperament with an approximate 77/64 generator of 7\26, with mos scales of size 7, 11 and 15. The [-3 0 0 6 -4⟩ comma leads to a half-octave period and an approximate 49/44 generator of 4\26, leading to mos of size 8 and 14.
  4. We can also treat 26edo as a full 13-limit temperament, since it is consistent on the 13-odd-limit (unlike all lower edos).
  5. It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fourths give a 17:14 and four fifths give a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and 33edo even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.

Its step of 46.2 ¢, as well as the octave-inverted and octave-equivalent versions of it, holds the distinction for having around the highest harmonic entropy possible. In other words, there is a common perception of quartertones as being the most dissonant intervals. This property is shared with all edos between around 20 and 30. Intervals smaller than this tend to be perceived as unison and are more consonant as a result; intervals larger than this have less "tension" and thus are also more consonant.

Thanks to its sevenths, 26edo is an ideal tuning for its size for metallic harmony.

Odd harmonics

Approximation of odd harmonics in 26edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -9.6 -17.1 +0.4 -19.3 +2.5 -9.8 +19.4 -12.6 -20.6 -9.2 +17.9
Relative (%) -20.9 -37.0 +0.9 -41.8 +5.5 -21.1 +42.1 -27.4 -44.6 -20.0 +38.7
Steps
(reduced) 		41
(15) 		60
(8) 		73
(21) 		82
(4) 		90
(12) 		96
(18) 		102
(24) 		106
(2) 		110
(6) 		114
(10) 		118
(14)

Subsets and supersets

26edo has 2edo and 13edo as subsets, of which 13edo is non-trivial, sharing harmonics 5 and 9 through 23 (including direct approximations) with 26edo. Multiplying 26edo by 3 yields 78edo, which corrects several harmonics.

Intervals

Degrees Cents Approximate ratios[note 1] Interval
name 		Example
in D 		SKULO
Interval name 		Example
in D 		Solfeges
0 0.00 1/1 P1 D P1 D da do
1 46.15 33/32, 49/48, 36/35, 25/24 A1 D# A1, S1 D#, SD du di
2 92.31 21/20, 22/21, 26/25 d2 Ebb sm2 sEb fro rih
3 138.46 12/11, 13/12, 14/13, 16/15 m2 Eb m2 Eb fra ru
4 184.62 9/8, 10/9, 11/10 M2 E M2 E ra re
5 230.77 8/7, 15/13 A2 E# SM2 SE ru ri
6 276.92 7/6, 13/11, 33/28 d3 Fb sm3 sF no ma
7 323.08 135/112, 6/5 m3 F m3 F na me
8 369.23 5/4, 11/9, 16/13 M3 F# M3 F# ma muh/mi
9 415.38 9/7, 14/11, 33/26 A3 Fx SM3 SF# mu maa
10 461.54 21/16, 13/10 d4 Gb s4 sG fo fe
11 507.69 75/56, 4/3 P4 G P4 G fa fa
12 553.85 11/8, 18/13 A4 G# A4 G# fu/pa fu
13 600.00 7/5, 10/7 AA4, dd5 Gx, Abb SA4, sd5 SG#, sAb pu/sho fi/se
14 646.15 16/11, 13/9 d5 Ab d5 Ab sha/so su
15 692.31 112/75, 3/2 P5 A P5 A sa sol
16 738.46 32/21, 20/13 A5 A# S5 SA su si
17 784.62 11/7, 14/9 d6 Bbb sm6 sBb flo leh
18 830.77 13/8, 8/5 m6 Bb m6 Bb fla le/lu
19 876.92 5/3, 224/135 M6 B M6 B la la
20 923.08 12/7, 22/13 A6 B# SM6 SB lu li
21 969.23 7/4, 26/15 d7 Cb sm7 sC tho ta
22 1015.38 9/5, 16/9, 20/11 m7 C m7 C tha te
23 1061.54 11/6, 13/7, 15/8, 24/13 M7 C# M7 C# ta tu/ti
24 1107.69 21/11, 25/13, 40/21 A7 Cx SM7 SC# tu to
25 1153.85 64/33, 96/49, 35/18, 48/25 d8 Db d8, s8 Db, sD do da
26 1200.00 2/1 P8 D P8 D da do

Interval quality and chord names in color notation

Using color notation, qualities can be loosely associated with colors:

Quality Color Monzo Format Examples
diminished zo {a, b, 0, 1} 7/6, 7/4
minor fourthward wa {a, b}, b < -1 32/27, 16/9
" gu {a, b, -1} 6/5, 9/5
major yo {a, b, 1} 5/4, 5/3
" fifthward wa {a, b}, b > 1 9/8, 27/16
augmented ru {a, b, 0, -1} 9/7, 12/7

All 26edo chords can be named using conventional methods, expanded to include augmented and diminished 2nd, 3rds, 6ths and 7ths. Spelling certain chords properly may require triple sharps and flats, especially if the tonic is anything other than the 11 keys in the Eb-C# range. Here are the zo, gu, yo and ru triads:

Color of the 3rd JI chord Notes as Edosteps Notes of C Chord Written Name Spoken Name
zo 6:7:9 0-6-15 C Ebb G C(b3) or C(d3) C flat-three or C dim-three
gu 10:12:15 0-7-15 C Eb G Cm C minor
yo 4:5:6 0-8-15 C E G C C major or C
ru 14:18:21 0-9-15 C E# G C(#3) or C(A3) C sharp-three or C aug-three

For a more complete list, see Ups and downs notation #Chord names in other EDOs.

Notation

Sagittal notation

This notation uses the same sagittal sequence as EDOs 5, 12, and 19, is a subset of the notation for 52-EDO, and is a superset of the notation for 13-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation

Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation

Approximation to JI

15-odd-limit interval mappings

The following tables show how 15-odd-limit intervals are represented in 26edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 26edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/12, 24/13 0.111 0.2
7/4, 8/7 0.405 0.9
11/7, 14/11 2.123 4.6
9/5, 10/9 2.212 4.8
11/8, 16/11 2.528 5.5
13/10, 20/13 7.325 15.9
5/3, 6/5 7.436 16.1
13/9, 18/13 9.536 20.7
3/2, 4/3 9.647 20.9
13/8, 16/13 9.758 21.1
7/6, 12/7 10.052 21.8
13/7, 14/13 10.163 22.0
11/6, 12/11 12.176 26.4
13/11, 22/13 12.287 26.6
15/11, 22/15 16.895 36.6
15/13, 26/15 16.972 36.8
5/4, 8/5 17.083 37.0
7/5, 10/7 17.488 37.9
15/14, 28/15 19.019 41.2
9/8, 16/9 19.295 41.8
15/8, 16/15 19.424 42.1
11/10, 20/11 19.611 42.5
9/7, 14/9 19.699 42.7
11/9, 18/11 21.823 47.3
15-odd-limit intervals in 26edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/12, 24/13 0.111 0.2
7/4, 8/7 0.405 0.9
11/7, 14/11 2.123 4.6
9/5, 10/9 2.212 4.8
11/8, 16/11 2.528 5.5
13/10, 20/13 7.325 15.9
5/3, 6/5 7.436 16.1
13/9, 18/13 9.536 20.7
3/2, 4/3 9.647 20.9
13/8, 16/13 9.758 21.1
7/6, 12/7 10.052 21.8
13/7, 14/13 10.163 22.0
11/6, 12/11 12.176 26.4
13/11, 22/13 12.287 26.6
15/13, 26/15 16.972 36.8
5/4, 8/5 17.083 37.0
7/5, 10/7 17.488 37.9
9/8, 16/9 19.295 41.8
11/10, 20/11 19.611 42.5
9/7, 14/9 19.699 42.7
11/9, 18/11 21.823 47.3
15/8, 16/15 26.730 57.9
15/14, 28/15 27.135 58.8
15/11, 22/15 29.258 63.4

Approximation to irrational intervals

26edo approximates both acoustic phi (the golden ratio) and pi quite accurately. Not until 1076edo do we find a better edo in terms of relative error on these intervals.

Direct approximation
Interval Error (abs, ¢)
2ϕ / ϕ 0.858
ϕ 2.321
π 2.820
2ϕ 3.179
π/ϕ 5.141
2ϕ / π 5.999

Regular temperament properties

Subgroup Comma basis Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-41 26⟩ [⟨26 41]] +3.043 3.05 6.61
2.3.5 81/80, 78125/73728 [⟨26 41 60]] +4.489 3.22 6.98
2.3.5.7 50/49, 81/80, 405/392 [⟨26 41 60 73]] +3.324 3.44 7.45
2.3.5.7.11 45/44, 50/49, 81/80, 99/98 [⟨26 41 60 73 90]] +2.509 3.48 7.53
2.3.5.7.11.13 45/44, 50/49, 65/64, 78/77, 81/80 [⟨26 41 60 73 90 96]] +2.531 3.17 6.87
2.3.5.7.11.13.17 45/44, 50/49, 65/64 78/77, 81/80, 85/84 [⟨26 41 60 73 90 96 106]] +2.613 2.94 6.38
2.3.5.7.11.13.17.19 45/44, 50/49, 57/56, 65/64, 78/77, 81/80, 85/84 [⟨26 41 60 73 90 96 106 110]] +2.894 2.85 6.18
  • 26et is lower in relative error than any previous equal temperaments in the 17-, 19-, 23-, and 29-limit (using the 26i val for the 23- and 29-limit). The next equal temperaments performing better in those subgroups are 27eg, 27eg, 29g, and 46, respectively.

Rank-2 Temperaments

Important mos scales include (in addition to ones found in 13edo):

  • Flattone[7] (diatonic) 4443443 (15\26, 1\1)
  • Flattone[12] (chromatic) 313131331313 (15\26, 1\1)
  • Flattone[19] (enharmonic) 2112112112121121121 (15\26, 1\1)
  • Orgone[7] 5525252 (7\26, 1\1)
  • Orgone[11] 32322322322 (7\26, 1\1)
  • Orgone[15] 212212221222122 (7\26, 1\1)
  • Lemba[6] 553553 (5\26, 1\2)
  • Lemba[10] 3232332323 (5\26, 1\2)
  • Lemba[16] 2122122121221221 (5\26, 1\2)
Periods
per 8ve 		Generator Temperaments
1 1\26 Quartonic / quarto
1 3\26 Glacier / bleu / jerome / secund
1 5\26 Cynder / mothra
1 7\26 Orgone / superkleismic
1 9\26 Wesley / roman
1 11\26 Flattone / flattertone
2 1\26 Elvis
2 2\26 Injera
2 3\26 Fifive / crepuscular
2 4\26 Dubbla
Unidec / hendec
2 5\26 Lemba
2 6\26 Doublewide / cavalier
13 1\26 Triskaidekic

Hendec in 26et

Hendec, the 13-limit 26 & 46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.

Commas

26et tempers out the following commas. This assumes the val ⟨26 41 60 73 90 96].

Prime
limit 		Ratio[note 2] Monzo Cents Color name Name(s)
5 81/80 [-4 4 -1⟩ 21.51 Gu Syntonic comma, Didymos comma, meantone comma
5 (60 digits) [-17 62 -35⟩ 0.23 Quadla-sepquingu Senior comma
7 525/512 [-9 1 2 1⟩ 43.41 Lazoyoyo Avicennma, Avicenna's enharmonic diesis
7 50/49 [1 0 2 -2⟩ 34.98 Biruyo Jubilisma, tritonic diesis
7 875/864 [-5 -3 3 1⟩ 21.90 Zotriyo Keema
7 4000/3969 [5 -4 3 -2⟩ 13.47 Sarurutriyo Octagar comma
7 1728/1715 [6 3 -1 -3⟩ 13.07 Triru-agu Orwellisma
7 1029/1024 [-10 1 0 3⟩ 8.43 Latrizo Gamelisma
7 (12 digits) [-9 8 -4 2⟩ 8.04 Labizogugu Varunisma
7 (18 digits) [-26 -1 1 9⟩ 3.79 Latritrizo-ayo Wadisma
7 4375/4374 [-1 -7 4 1⟩ 0.40 Zoquadyo Ragisma
11 99/98 [-1 2 0 -2 1⟩ 17.58 Loruru Mothwellsma
11 100/99 [2 -2 2 0 -1⟩ 17.40 Luyoyo Ptolemisma
11 65536/65219 [16 0 0 -2 -3⟩ 8.39 Satrilu-aruru Orgonisma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
11 441/440 [-3 2 -1 2 -1⟩ 3.93 Luzozogu Werckisma
11 3025/3024 [-4 -3 2 -1 2⟩ 0.57 Loloruyoyo Lehmerisma
11 9801/9800 [-3 4 -2 -2 2⟩ 0.18 Bilorugu Kalisma, Gauss' comma
13 105/104 [-3 1 1 1 0 -1⟩ 16.57 Thuzoyo Animist comma

Scales

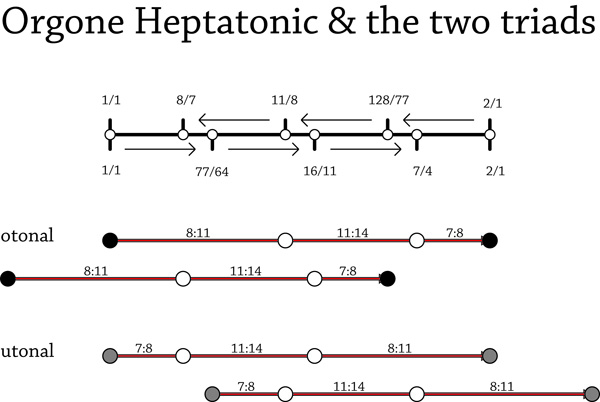
Orgone temperament

Andrew Heathwaite first proposed orgone temperament to take advantage of 26edo's excellent 11 and 7 approximations. 7 degrees of 26edo is a wide minor third of approximately 323.077 cents, and that interval taken as a generator produces 7-tone and 11-tone MOS scales:

The 7-tone scale in degrees-in-between: 5 2 5 2 5 2 5. MOS of type 4L 3s (mish).

The 7-tone scale in cents: 0 231 323 554 646 877 969 1200.

The 11-tone scale in degrees-in-between: 2 3 2 2 3 2 3 2 2 3 2. MOS of type 4L 7s.

The 11-tone scale in cents: 0 92 231 323 415 554 646 785 877 969 1108 1200.

The primary triad for orgone temperament is 8:11:14 and its subharmonic inversion, which these scales have in abundance. 2g approximates 16:11 and 3g approximates 7:4 (and I would call that the definition of Orgone Temperament). That also implies that g approximates the difference between 7:4 and 16:11, which is 77:64, about 320.1 cents.

orgone_heptatonic.jpg

Additional scalar bases available

Since the perfect 5th in 26edo spans 15 degrees, it can be divided into three equal parts (each approximately an 8/7) as well as five equal parts (each approximately a 13/12). The former approach produces MOS at 1L+4s, 5L+1s, and 5L+6s (5 5 5 5 6, 5 5 5 5 5 1, and 4 1 4 1 4 1 4 1 4 1 1 respectively), and is excellent for 4:6:7 triads. The latter produces MOS at 1L+7s and 8L+1s (3 3 3 3 3 3 3 5 and 3 3 3 3 3 3 3 3 2 respectively), and is fairly well-supplied with 4:6:7:11:13 pentads. It also works well for more conventional (though further from Just) 6:7:9 triads, as well as 4:5:6 triads that use the worse mapping for 5 (making 5/4 the 415.38-cent interval).

-Igs

MOS scales

See List of MOS scales in 26edo

Instruments

James Fenn's midi keyboard.

Literature

Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.

Music

See also: Category:26edo tracks

Modern renderings

Johann Sebastian Bach
Nicolaus Bruhns

21st century

Abnormality
Jim Aikin
Beheld
benyamind
Cameron Bobro
CellularAutomaton
City of the Asleep
Zach Curley
Bryan Deister
Ebooone
Francium
Igliashon Jones
Melopœia
Claudi Meneghin
Microtonal Maverick (formerly The Xen Zone)
Herman Miller
Shaahin Mohajeri
Mundoworld
NullPointerException Music
Ray Perlner
Sevish
Jon Lyle Smith
Tapeworm Saga
Uncreative Name
Chris Vaisvil

Notes

  1. ↑ Based on treating 26edo as a 13-limit temperament; other approaches are also possible.
  2. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Retrieved from "https://en.xen.wiki/index.php?title=26edo&oldid=207042"