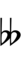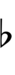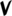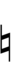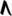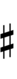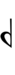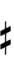17edo

From Xenharmonic Wiki
(Redirected from 17-EDO instruments)
Jump to navigation Jump to search
← 16edo 17edo 18edo →
Prime factorization 17 (prime)
Step size 70.5882¢ 
Fifth 10\17 (705.882¢)
(semiconvergent)
Semitones (A1:m2) 2:1 (141.2¢ : 70.59¢)
Consistency limit 3
Distinct consistency limit 3

17 equal divisions of the octave (abbreviated 17edo or 17ed2), also called 17-tone equal temperament (17tet) or 17 equal temperament (17et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 17 equal parts of about 70.6 ¢ each. Each step represents a frequency ratio of 21/17, or the 17th root of 2.

English Wikipedia has an article on:

Theory

17edo's perfect fifth is around 4 cents sharp of just, and around 6 cents sharp of 12edo's, lending itself to an expressive diatonic scale. Meanwhile, it approximates harmonics 7, 11, 13, and 23 to reasonable degrees, despite completely missing harmonic 5. Thus it can plausibly be treated as a 2.3.25.7.11.13.23 subgroup temperament, for which it is quite accurate (though the 7-limit ratios are generally not as well-represented as those of the other integers). Because these harmonics are all tempered sharp, it adapts well to octave shrinking; 27edt (a variant of 17edo in which the octaves are flattened by ~2.5 cents) is a good alternative. Another one is 44ed6.

Because the 5th harmonic is not well-approximated, using timbres with attenuated 5th harmonics (and its multiples) may reduce audible beating.

The standard major triad is quite dissonant as the major third is closer to 9/7 than the traditional 5/4. Instead, the tonic chords of 17edo could be considered to be the tetrad 6:7:8:9 and its utonal inversion (representing 14:16:18:21 as 64/63 is tempered out), the former of which is a subminor chord with added fourth, and the latter a supermajor chord with added second (resembling the mu chord of Steely Dan fame). These are realized in 17edo as 0-4-7-10 and 0-3-6-10, respectively. Both of these have distinct moods, and are stable and consonant, if somewhat more sophisticated than their classic 5-limit counterparts. To this group we could also add the 0-3-7-10 (which is a sus4 with added second, or sus2 with added fourth). These three chords comprise the three ways to divide the 17edo perfect fifth into two whole tones and one subminor third. Chromatic alterations of them also exist, for example, the 0-3-7-10 chord may be altered to 0-2-7-10 (which approximates 12:13:16:18) or 0-3-8-10 (which approximates 8:9:11:12). The 0-3-8-10 chord is impressive-sounding, resembling a sus4 but with even more tension; it resolves quite nicely to 0-3-6-10.

Another construction of septimal chords involves 4:7:12 and its inversion 7:12:21. These triads span a twelfth, realized in 17edo as 0-14-27 and 0-13-27, respectively. To this we may add 0-12-14-27, representing 8:13:14:24, or 0-13-15-27, representing 7:12:13:21.

In the no-5 13-odd-limit, 17edo maintains the smallest relative error⁠ ⁠[clarification needed ] of any edo until 166edo.

Odd harmonics

Approximation of odd harmonics in 17edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +3.9 -33.4 +19.4 +7.9 +13.4 +6.5 -29.4 -34.4 -15.2 +23.3 +7.0
Relative (%) +5.6 -47.3 +27.5 +11.1 +19.0 +9.3 -41.7 -48.7 -21.5 +33.1 +9.9
Steps
(reduced) 		27
(10) 		39
(5) 		48
(14) 		54
(3) 		59
(8) 		63
(12) 		66
(15) 		69
(1) 		72
(4) 		75
(7) 		77
(9)

Subsets and supersets

17edo is the seventh prime edo, following 13edo and coming before 19edo. 34edo, which doubles it, provides a good correction to harmonics 5 and 17.

Intervals

See also: 17edo solfege
# Cents Approximate ratios[note 1] Circle-of-fifths notation† Ups and downs notation
(EUs: vvA1 and ^d2) 		SKULO notation (U = 1) 3L 4s notation
0 0.00 1/1 Unison D unison P1 D unison P1 D unison D
1 70.59 24/23, 25/24, 26/25, 27/26, 28/27 Minor 2nd
(Semiaugmented 1sn) 		Eb
(Dt) 		up unison,
minor 2nd 		^1, m2 Eb uber unison,
minor 2nd 		U1, m2 UD, Eb augmented 1sn D#
2 141.18 12/11, 13/12, 14/13, 25/23 Augmented 1sn
(Neutral 2nd) 		D#
(Ed) 		augmented 1sn,
mid 2nd 		A1, ~2 vE neutral 2nd N2 UEb, uE minor 2nd Eb
3 211.76 8/7, 9/8, 17/15, 25/22, 26/23 Major 2nd E major 2nd M2 E major 2nd M2 E major 2nd E
4 282.35 7/6, 13/11, 20/17 Minor 3rd F minor 3rd m3 F minor 3rd m3 F diminished 3rd Fb
5 352.94 11/9, 27/22, 16/13, 39/32 Diminished 4th
(Neutral 3rd) 		Gb
(Ft) 		mid 3rd ~3 ^F neutral 3rd N3 UF, uF# perfect 3rd F
6 423.53 9/7, 14/11, 23/18, 32/25, 51/40 Major 3rd
(Semidiminished 4th) 		F#
(Gd) 		major 3rd M3 F# major 3rd M3 F# augmented 3rd F#
7 494.12 4/3, 21/16, 85/64 Perfect 4th G perfect 4th P4 G perfect 4th P4 G minor 4th G
8 564.71 11/8, 18/13, 25/18, 32/23 Diminished 5th
(Semiaugmented 4th) 		Ab
(Gt) 		mid 4th,
diminished 5th 		~4, d5 ^G, Ab uber 4th/
neutral 4th 		U4/N4 UG major 4th G#
9 635.29 13/9, 16/11, 23/16, 36/25 Augmented 4th
(Semidiminished 5th) 		G#
(Ad) 		augmented 4th,
mid 5th 		A4, ~5 G#, vA unter 5th/
neutral 5th 		u5/N5 uA minor 5th Ab
10 705.88 3/2, 32/21, 128/85 Perfect 5th A perfect 5th P5 A perfect 5th P5 A major 5th A
11 776.47 11/7, 14/9, 25/16, 36/23, 80/51 Minor 6th
(Semiaugmented 5th) 		Bb
(At) 		minor 6th m6 Bb minor 6th m6 Bb diminished 6th Bb
12 847.06 13/8, 18/11, 44/27, 64/39 Augmented 5th
(Neutral 6th) 		A#
(Bd) 		mid 6th ~6 vB neutral 6th N6 UBb, uB perfect 6th B
13 917.65 12/7, 17/10, 22/13 Major 6th B major 6th M6 B major 6th M6 B augmented 6th B#
14 988.24 7/4, 16/9, 23/13, 30/17, 44/25 Minor 7th C minor 7th m7 C minor 7th m7 C minor 7th Cb
15 1058.82 11/6, 13/7, 24/13, 46/25 Diminished 8ve
(Neutral 7th) 		Db
(Ct) 		mid 7th ~7 ^C neutral 7th N7 UC, uC# major 7th C
16 1129.41 23/12, 25/13, 27/14, 48/25, 52/27 Major 7th
(Semidiminished 8ve) 		C#
(Dd) 		major 7th,
down 8ve 		M7, v8 C# major 7th,
unter octave 		M7, u8 C#, uD diminished 8ve Db
17 1200.00 2/1 Octave D octave P8 D octave P8 D octave D

† Half-sharps and half-flats (denoted "t" and "d", respectively) can be used to alter the note by a single step, since sharps and flats each span two edosteps. Using half-sharps and half-flats may be preferable for compatibility with the ups-and-downs notation in 34edo, in which an up or down respectively constitute a quarter-sharp or quarter-flat.

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality Color Monzo Format Examples
minor zo (a, b, 0, 1) 7/6, 7/4
fourthward wa (a, b), b < -1 32/27, 16/9
mid ilo (a, b, 0, 0, 1) 11/9, 11/6
lu (a, b, 0, 0, -1) 12/11, 18/11
major fifthward wa (a, b), b > 1 9/8, 27/16
ru (a, b, 0, -1) 9/7, 12/7

All 17edo chords can be named using ups and downs. Here are the zo, ilo and ru triads:

Color of the 3rd JI Chord Notes as Edosteps Notes of C Chord Written Name Spoken Name
zo 6:7:9 0-4-10 C Eb G Cm C minor
ilo 18:22:27 0-5-10 C vE G C~ C mid
ru 14:18:21 0-6-10 C E G C C major or C

Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

0-4-9 = C Eb vG = Cm(v5) = C minor down-five

0-5-9 = C vE vG = C~(v5) = C mid down-five

0-6-11 = C E ^G = C(^5) = C up-five

0-4-10-14 = C Eb G Bb = Cm7 = C minor seven

0-5-10-14 = C vE G Bb = C~,7 = C mid add seven

0-6-10-15 = C E G vB = C,~7 = C add mid-seven

0-5-10-15 = C vE G vB = C~7 = C mid-seven

For a more complete list, see Ups and downs notation #Chords and Chord Progressions.

Notation

Quarter tone notation

Since a sharp raises by 2 steps, 17edo can be notated using quarter-tone accidentals.

Step Offset −4 −3 −2 −1 0 +1 +2 +3 +4
Symbol
Heji4.svg
HeQd3.svg
Heji11.svg
HeQd1.svg
Heji18.svg
HeQu1.svg
Heji25.svg
HeQu3.svg
Heji32.svg

Sagittal

From the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 17edo in the Revo flavor of Sagittal:

17edo Sagittal.png

Approximation to JI

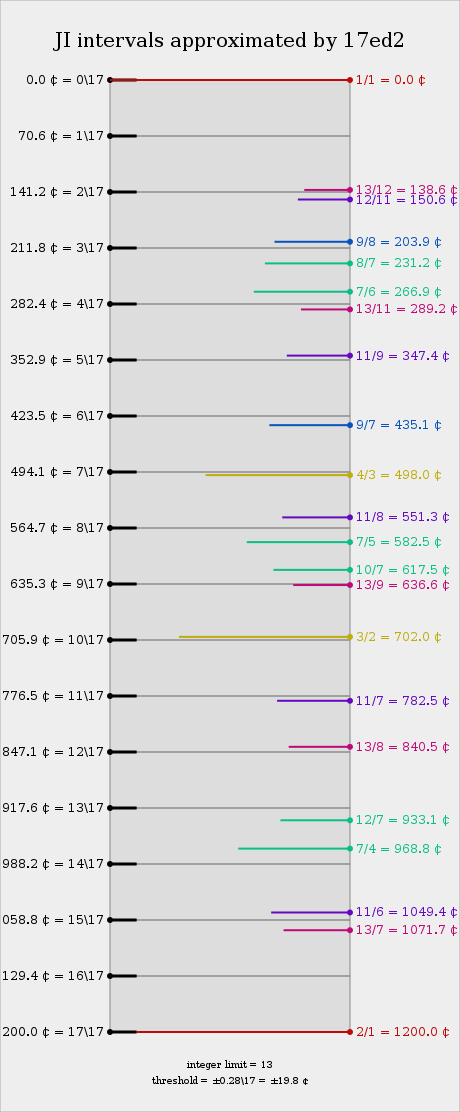
15-odd-limit interval mappings

The following tables show how 15-odd-limit intervals are represented in 17edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 17edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/9, 18/13 1.324 1.9
13/12, 24/13 2.604 3.7
3/2, 4/3 3.927 5.6
11/9, 18/11 5.533 7.8
11/7, 14/11 6.021 8.5
13/8, 16/13 6.531 9.3
13/11, 22/13 6.857 9.7
9/8, 16/9 7.855 11.1
11/6, 12/11 9.461 13.4
9/7, 14/9 11.555 16.4
13/7, 14/13 12.878 18.2
11/8, 16/11 13.388 19.0
7/6, 12/7 15.482 21.9
7/5, 10/7 17.806 25.2
7/4, 8/7 19.409 27.5
15/14, 28/15 21.734 30.8
11/10, 20/11 23.828 33.8
15/11, 22/15 27.755 39.3
9/5, 10/9 29.361 41.6
15/8, 16/15 29.445 41.7
13/10, 20/13 30.685 43.5
5/3, 6/5 33.288 47.2
5/4, 8/5 33.373 47.3
15/13, 26/15 34.612 49.0
15-odd-limit intervals in 17edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/9, 18/13 1.324 1.9
13/12, 24/13 2.604 3.7
3/2, 4/3 3.927 5.6
11/9, 18/11 5.533 7.8
11/7, 14/11 6.021 8.5
13/8, 16/13 6.531 9.3
13/11, 22/13 6.857 9.7
9/8, 16/9 7.855 11.1
11/6, 12/11 9.461 13.4
9/7, 14/9 11.555 16.4
13/7, 14/13 12.878 18.2
11/8, 16/11 13.388 19.0
7/6, 12/7 15.482 21.9
7/4, 8/7 19.409 27.5
15/8, 16/15 29.445 41.7
5/4, 8/5 33.373 47.3
15/13, 26/15 35.976 51.0
5/3, 6/5 37.300 52.8
13/10, 20/13 39.904 56.5
9/5, 10/9 41.227 58.4
15/11, 22/15 42.833 60.7
11/10, 20/11 46.760 66.2
15/14, 28/15 48.855 69.2
7/5, 10/7 52.782 74.8

Selected 13-limit intervals

alt : Your browser has no SVG support.

Tuning by ear

17edo is very close to a circle of seventeen 25/24 chromatic semitones: (25/24)^17 is only 1.43131 cents sharp of an octave. This means that if you can tune seventeen 25/24's accurately (by say, tuning 5/4 up, 3/2 down and 5/4 up, taking care to minimize the error at each step), you have a shot at approximating 17edo within melodic just noticeable difference.

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [27 -17⟩ [⟨17 27]] −1.24 1.24 1.76
2.3.7 64/63, 17496/16807 [⟨17 27 48]] −3.13 2.85 4.05
2.3.7.11 64/63, 99/98, 243/242 [⟨17 27 48 59]] −3.31 2.49 3.54
2.3.7.11.13 64/63, 78/77, 99/98, 144/143 [⟨17 27 48 59 63]] −3.00 2.31 3.28
  • 17et is lower in relative error than any previous equal temperaments in the no-5 11- and 13-limit. The next equal temperaments doing better in these subgroups are 41 and 207, respectively.

Uniform maps

13-limit uniform maps between 16.5 and 17.5
Min. size Max. size Wart notation Map
16.5000 16.5636 17bccdddeeefff ⟨17 26 38 46 57 61]
16.5636 16.5810 17bccdeeefff ⟨17 26 38 47 57 61]
16.5810 16.6196 17bdeeefff ⟨17 26 39 47 57 61]
16.6196 16.6212 17bdeeef ⟨17 26 39 47 57 62]
16.6212 16.7196 17bdef ⟨17 26 39 47 58 62]
16.7196 16.8899 17def ⟨17 27 39 47 58 62]
16.8899 16.9103 17de ⟨17 27 39 47 58 63]
16.9103 16.9198 17d ⟨17 27 39 47 59 63]
16.9198 17.0117 17 ⟨17 27 39 48 59 63]
17.0117 17.1601 17c ⟨17 27 40 48 59 63]
17.1601 17.1994 17cff ⟨17 27 40 48 59 64]
17.1994 17.2760 17ceeff ⟨17 27 40 48 60 64]
17.2760 17.3506 17cddeeff ⟨17 27 40 49 60 64]
17.3506 17.4304 17bbcddeeff ⟨17 28 40 49 60 64]
17.4304 17.4424 17bbcddeeffff ⟨17 28 40 49 60 65]
17.4424 17.4884 17bbcccddeeffff ⟨17 28 41 49 60 65]
17.4884 17.5000 17bbcccddeeeeffff ⟨17 28 41 49 61 65]

Commas

17et tempers out the following commas. (Note: This assumes patent val ⟨17 27 39 48 59 63 69], cent values ​​rounded to 5 digits.)

Prime
limit 		Ratio[1] Monzo Cents Color name Name
3 (18 digits) [27 -17⟩ 66.765 Sasawa 17-comma
5 25/24 [-3 -1 2⟩ 70.762 Yoyo Dicot comma
5 32805/32768 [-15 8 1⟩ 1.9537 Layo Schisma
7 525/512 [-9 1 2 1⟩ 43.408 Lazoyoyo Avicennma
7 64/63 [6 -2 0 -1⟩ 27.264 Ru Septimal comma
7 245/243 [0 -5 1 2⟩ 14.191 Zozoyo Sensamagic comma
7 1728/1715 [6 3 -1 -3⟩ 13.074 Triru-agu Orwellisma
7 (12 digits) [-6 -8 2 5⟩ 1.1170 Quinzo-ayoyo Wizma
11 99/98 [-1 2 0 -2 1⟩ 17.576 Loruru Mothwellsma
11 896/891 [7 -4 0 1 -1⟩ 9.6880 Saluzo Pentacircle comma
11 243/242 [-1 5 0 0 -2⟩ 7.1391 Lulu Rastma
11 385/384 [-7 -1 1 1 1⟩ 4.5026 Lozoyo Keenanisma
13 1352/1331 [3 0 0 0 -3 2⟩ 27.101 Bithotrilu Lovecraft comma
13 364/363 [2 -1 0 1 -2 1⟩ 4.763 Tholuluzo Minor minthma
17 136/135 [3 -3 -1 0 0 0 1⟩ 12.776 Sogu 2nd Diatisma

Note that despite their relatively large size, the 17-comma, the avicennma and the chromatic semitone are all tempered out by the 13-limit patent val, as stated.

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator Cents Associated
ratio 		Temperament
1 2\17 141.18 13/12 Bleu / progression (17c) / glacier
1 3\17 211.76 8/7~9/8 Machine
1 4\17 282.35 13/11 Huxley / lovecraft / subklei (17c)
1 5\17 352.94 11/9 Suhajira / neutrominant (17c) / beatles (17c) / dicotic (17)
Hemif / mohamaq (17c) / salsa (17)
1 6\17 423.53 9/7 Skwares / squares (17c) / sentinel (17) / sidi (17)
1 7\17 494.12 4/3 Archy / supra / quasisuper (17c) / dominant (17c) / superpyth (17) / schism (17)
Fiventeen
1 8\17 564.71 7/5 Lee / liese (17c) / pycnic (17)
Progress (17c)

Scales

MOS scales

Main article: MOS scales of 17edo
  • diatonic (leapfrog/archy) 5L 2s 3 3 3 1 3 3 1 (10\17, 1\1)
  • neutrominant 3L 4s 3 2 3 2 3 2 2 (5\17, 1\1)
  • neutrominant 7L 3s 2 2 2 1 2 2 1 2 2 1 (5\17, 1\1)
  • squares 3L 5s 1 1 4 1 4 1 4 (6\17, 1\1)
  • squares 3L 8s 1 3 1 1 3 1 1 3 (6\17, 1\1)
  • Pathological squares 3L 11s 1 1 2 1 1 1 2 1 1 1 2 (6\17, 1\1)
  • lovecraft 4L 5s 3 1 3 1 3 1 3 1 1 (4\17, 1\1)
  • Pathological 1L 13s 4 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)
  • Pathological 1L 14s 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)
  • Pathological 2L 13s 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 (8\17, 1\1)
  • Pathological 1L 15s 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)

Well temperaments

Introductory materials

Music

Main article: 17edo/Music
See also: Category:17edo tracks
YouTube playlist of 17edo pieces
YouTube videos tagged with 17edo
Compositions from the Seventeen Tone Piano Project

Instruments

External image: http://sphotos.ak.fbcdn.net/hphotos-ak-snc4/hs883.snc4/71639_167001659983806_100000219181856_601995_1526184_n.jpg ⁠ ⁠[dead link]

WARNING: MediaWiki doesn't have very good support for external images.
Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.

External image: http://sphotos.ak.fbcdn.net/hphotos-ak-ash2/hs382.ash2/66019_167001006650538_100000219181856_601987_48585_n.jpg ⁠ ⁠[dead link]

WARNING: MediaWiki doesn't have very good support for external images.
Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.

17P1050829r.JPG

  • 17edo soprano Harmony ukulele with a 3D printed fretboard - conversion by Tristan Bay

17edo soprano ukulele with 3D printed fretboard.jpg

See also

Notes

  1. ↑ Based on treating 17edo as a 2.3.25.7.11.13.85.23 subgroup temperament; other approaches are also possible.
  1. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Retrieved from "https://en.xen.wiki/index.php?title=17edo&oldid=172884#Instruments"