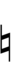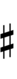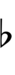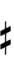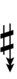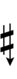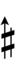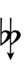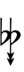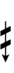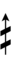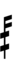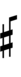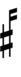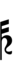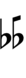58edo
| ← 57edo | 58edo | 59edo → |
58 equal divisions of the octave (abbreviated 58edo or 58ed2), also called 58-tone equal temperament (58tet) or 58 equal temperament (58et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 58 equal parts of about 20.7 ¢ each. Each step represents a frequency ratio of 21/58, or the 58th root of 2.
Theory
58edo is a strong system in the 11-, 13- and 17-limit. It is the smallest edo which is consistent through the 17-odd-limit, and is also the smallest distinctly consistent in the 11-odd-limit (the first equal temperament to map the entire 11-odd-limit tonality diamond to distinct scale steps), and hence the first which can define a tempered version of the famous 43-note Genesis scale of Harry Partch.
While the 17th harmonic is a cent and a half flat, the harmonics below it are all a little sharp, giving it the sound of a sharp system. Since 58 = 2 × 29, 58edo shares the same excellent perfect fifth with 29edo. It is the last edo to have exactly one diatonic perfect fifth and no 5edo or 7edo fifths.
As an equal temperament, 58et tempers out 2048/2025 in the 5-limit; 126/125, 1728/1715, and 5120/5103 in the 7-limit; 176/175, 243/242, 441/440, 540/539, and 896/891 in the 11-limit; 144/143, 351/350, 364/363 in the 13-limit. It supports hemififths, myna, diaschismic, harry, mystery, buzzard, thuja temperaments plus a number of gravity family extensions, and supplies the optimal patent val for the 7-, 11- and 13-limit diaschismic, 11- and 13-limit hemififths, 11- and 13-limit thuja, and 13-limit myna. It also supplies the optimal patent val for the 13-limit rank-3 temperaments thrush, bluebird, aplonis and jofur.
Of all edos which map the syntonic comma (81/80) to 1 step by patent val, 58edo is the one with the step size closest to 81/80, with one step of 58edo being less than 1 ¢ narrower than the just interval.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | +1.49 | +6.79 | +3.59 | +7.30 | +7.75 | -1.51 | -7.86 | -7.58 | +4.91 | -7.10 |
| Relative (%) | +0.0 | +7.2 | +32.8 | +17.3 | +35.3 | +37.4 | -7.3 | -38.0 | -36.7 | +23.7 | -34.3 | |
| Steps (reduced) |
58 (0) |
92 (34) |
135 (19) |
163 (47) |
201 (27) |
215 (41) |
237 (5) |
246 (14) |
262 (30) |
282 (50) |
287 (55) | |
Octave stretch
58edo's approximations of harmonics 3, 5, 7, 11, and 13 can all be improved if slightly compressing the octave is acceptable, using tunings such as 92edt or 150ed6.
Subsets and supersets
58edo contains 2edo and 29edo as subsets.
Intervals
| # | Cents | Approximate ratios* | Ups and downs notation |
|---|---|---|---|
| 0 | 0.0 | 1/1 | D |
| 1 | 20.7 | 56/55, 64/63, 81/80, 91/90, 105/104 | ^D, v3E♭ |
| 2 | 41.4 | 36/35, 40/39, 45/44, 49/48, 50/49, 55/54 | ^^D, vvE♭ |
| 3 | 62.1 | 26/25, 27/26, 28/27, 33/32 | ^3D, vE♭ |
| 4 | 82.8 | 21/20, 22/21, 25/24 | vvD♯, E♭ |
| 5 | 103.4 | 16/15, 17/16, 18/17 | vD♯, ^E♭ |
| 6 | 124.1 | 14/13, 15/14 | D♯, ^^E♭ |
| 7 | 144.8 | 12/11, 13/12 | ^D♯, v3E |
| 8 | 165.5 | 11/10 | ^^D♯, vvE |
| 9 | 186.2 | 10/9 | ^3D♯, vE |
| 10 | 206.9 | 9/8, 17/15 | E |
| 11 | 227.6 | 8/7 | ^E, v3F |
| 12 | 248.3 | 15/13 | ^^E, vvF |
| 13 | 269.0 | 7/6 | ^3E, vF |
| 14 | 289.7 | 13/11, 20/17 | F |
| 15 | 310.3 | 6/5 | ^F, v3G♭ |
| 16 | 331.0 | 17/14, 40/33 | ^^F, vvG♭ |
| 17 | 351.7 | 11/9, 16/13 | ^3F, vG♭ |
| 18 | 372.4 | 21/17, 26/21 | vvF♯, G♭ |
| 19 | 393.1 | 5/4 | vF♯, ^G♭ |
| 20 | 413.8 | 14/11 | F♯, ^^G♭ |
| 21 | 434.5 | 9/7 | ^F♯, v3G |
| 22 | 455.2 | 13/10, 17/13, 22/17 | ^^F♯, vvG |
| 23 | 475.9 | 21/16 | ^3F♯, vG |
| 24 | 496.6 | 4/3 | G |
| 25 | 517.2 | 27/20 | ^G, v3A♭ |
| 26 | 537.9 | 15/11 | ^^G, vvA♭ |
| 27 | 558.6 | 11/8, 18/13 | ^3G, vA♭ |
| 28 | 579.3 | 7/5 | vvG♯, A♭ |
| 29 | 600.0 | 17/12, 24/17 | vG♯, ^A♭ |
| 30 | 620.7 | 10/7 | G♯, ^^A♭ |
| 31 | 641.4 | 13/9, 16/11 | ^G♯, v3A |
| 32 | 662.1 | 22/15 | ^^G♯, vvA |
| 33 | 682.8 | 40/27 | ^3G♯, vA |
| 34 | 703.4 | 3/2 | A |
| 35 | 724.1 | 32/21 | ^A, v3B♭ |
| 36 | 744.8 | 17/11, 20/13, 26/17 | ^^A, vvB♭ |
| 37 | 765.5 | 14/9 | ^3A, vB♭ |
| 38 | 786.2 | 11/7 | vvA♯, B♭ |
| 39 | 806.9 | 8/5 | vA♯, ^B♭ |
| 40 | 827.6 | 21/13, 34/21 | A♯, ^^B♭ |
| 41 | 848.3 | 13/8, 18/11 | ^A♯, v3B |
| 42 | 869.0 | 28/17, 33/20 | ^^A♯, vvB |
| 43 | 889.7 | 5/3 | ^3A♯, vB |
| 44 | 910.3 | 17/10, 22/13 | B |
| 45 | 931.0 | 12/7 | ^B, v3C |
| 46 | 951.7 | 26/15 | ^^B, vvC |
| 47 | 972.4 | 7/4 | ^3B, vC |
| 48 | 993.1 | 16/9, 30/17 | C |
| 49 | 1013.8 | 9/5 | ^C, v3D♭ |
| 50 | 1034.5 | 20/11 | ^^C, vvD♭ |
| 51 | 1055.2 | 11/6, 24/13 | ^3C, vD♭ |
| 52 | 1075.9 | 13/7, 28/15 | vvC♯, D♭ |
| 53 | 1096.6 | 15/8, 17/9, 32/17 | vC♯, ^D♭ |
| 54 | 1117.2 | 21/11, 40/21, 48/25 | C♯, ^^D♭ |
| 55 | 1137.9 | 25/13, 27/14, 52/27, 64/33 | ^C♯, v3D |
| 56 | 1158.6 | 35/18, 39/20, 49/25, 88/45, 96/49, 108/55 | ^^C♯, vvD |
| 57 | 1179.3 | 55/28, 63/32, 160/81, 180/91, 208/105 | ^3C♯, vD |
| 58 | 1200.0 | 2/1 | D |
* As a 17-limit temperament
Notation
Ups and downs notation
58edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol |  |
|
|
|
 
|
|
|
|
|
|
|
|
|
| Flat symbol |
|
|
|
|
|
|
|
|
|
|
|
|
Half-sharps and half-flats can be used to avoid triple arrows:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
 |
|
|
|
|
|
 |
|
|
|
| Flat symbol |
|
|
 |
|
|
|
|
|
 |
|
|
|
Alternatively, a combination of quarter tone accidentals and arrow accidentals from Helmholtz–Ellis notation can be used.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
| Flat symbol |  |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
If double arrows are not desirable, then arrows can be attached to quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
 |
|
 |
|
|
|
 |
|
 |
|
|
|
| Flat symbol | |
 |
|
 |
|
|
|
 |
|
 |
|
|
|
Ivan Wyschnegradsky's notation
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
|
| Flat symbol |  |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
|
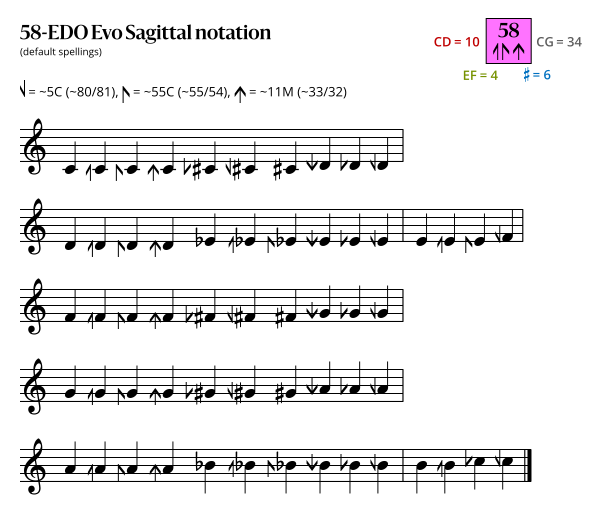
Sagittal notation
Evo flavor
Revo flavor
Evo-SZ flavor
Hemipyth notation
| # | Cents | Note names on D |
|---|---|---|
| 0 | 0.0 | D |
| 2 | 41.4 | α𝄳 |
| 5 | 103.4 | α |
| 7 | 144.8 | E𝄳 |
| 10 | 206.9 | E |
| 12 | 248.3 | β𝄳 |
| 14 | 289.7 | F |
| 15 | 310.3 | β |
| 17 | 351.7 | F‡ |
| 19 | 393.1 | γ |
| 22 | 455.2 | γ‡ |
| 24 | 496.6 | G |
| 27 | 558.6 | G‡ |
| 29 | 600.0 | δ |
| 31 | 641.4 | A𝄳 |
| 34 | 703.4 | A |
| 36 | 744.8 | ε𝄳 |
| 39 | 806.9 | ε |
| 41 | 848.3 | B𝄳 |
| 43 | 889.7 | ζ |
| 44 | 910.3 | B |
| 46 | 951.7 | ζ‡ |
| 48 | 993.1 | C |
| 51 | 1055.2 | C‡ |
| 53 | 1096.6 | η |
| 56 | 1158.6 | η‡ |
| 58 | 1200.0 | D |
Approximation to JI
Interval mappings
The following table shows how 15-odd-limit intervals are represented in 58edo. Prime harmonics are in bold.
As 58edo is consistent in the 15-odd-limit, the mappings by direct approximation and through the patent val are identical.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/11, 22/13 | 0.445 | 2.2 |
| 11/10, 20/11 | 0.513 | 2.5 |
| 15/13, 26/15 | 0.535 | 2.6 |
| 9/7, 14/9 | 0.601 | 2.9 |
| 13/10, 20/13 | 0.958 | 4.6 |
| 15/11, 22/15 | 0.980 | 4.7 |
| 3/2, 4/3 | 1.493 | 7.2 |
| 7/6, 12/7 | 2.095 | 10.1 |
| 9/8, 16/9 | 2.987 | 14.4 |
| 7/5, 10/7 | 3.202 | 15.5 |
| 7/4, 8/7 | 3.588 | 17.3 |
| 11/7, 14/11 | 3.715 | 18.0 |
| 9/5, 10/9 | 3.803 | 18.4 |
| 13/7, 14/13 | 4.160 | 20.1 |
| 11/9, 18/11 | 4.316 | 20.9 |
| 15/14, 28/15 | 4.695 | 22.7 |
| 13/9, 18/13 | 4.762 | 23.0 |
| 5/3, 6/5 | 5.296 | 25.6 |
| 11/6, 12/11 | 5.809 | 28.1 |
| 13/12, 24/13 | 6.255 | 30.2 |
| 5/4, 8/5 | 6.790 | 32.8 |
| 11/8, 16/11 | 7.303 | 35.3 |
| 13/8, 16/13 | 7.748 | 37.4 |
| 15/8, 16/15 | 8.283 | 40.0 |
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 289zpi | 58.066719 | 20.665883 | 7.814035 | 5.277671 | 1.358357 | 18.056292 | 1198.621202 | −1.378798 | 16 | 12 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3.5 | 2048/2025, 1594323/1562500 | [⟨58 92 135]] | −1.29 | 1.22 | 5.89 |
| 2.3.5.7 | 126/125, 1728/1715, 2048/2025 | [⟨58 92 135 163]] | −1.29 | 1.05 | 5.10 |
| 2.3.5.7.11 | 126/125, 176/175, 243/242, 896/891 | [⟨58 92 135 163 201]] | −1.45 | 1.00 | 4.83 |
| 2.3.5.7.11.13 | 126/125, 144/143, 176/175, 196/195, 364/363 | [⟨58 92 135 163 201 215]] | −1.56 | 0.94 | 4.56 |
| 2.3.5.7.11.13.17 | 126/125, 136/135, 144/143, 176/175, 196/195, 364/363 | [⟨58 92 135 163 201 215 237]] | −1.28 | 1.10 | 5.33 |
- 58et has a lower relative error than any previous equal temperaments in the 13-limit, and the next equal temperament that does better in this subgroup is 72.
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 3\58 | 62.07 | 28/27 | Unicorn / alicorn / qilin |
| 1 | 11\58 | 227.59 | 8/7 | Gorgik |
| 1 | 13\58 | 268.97 | 7/6 | Infraorwell |
| 1 | 15\58 | 310.34 | 6/5 | Myna |
| 1 | 17\58 | 351.72 | 49/40 | Hemififths |
| 1 | 19\58 | 393.10 | 64/51 | Emmthird |
| 1 | 23\58 | 475.86 | 21/16 | Buzzard / subfourth |
| 1 | 27\58 | 558.62 | 11/8 | Thuja |
| 2 | 3\58 | 62.07 | 28/27 | Monocerus |
| 2 | 1\58 | 20.69 | 81/80 | Bicommatic |
| 2 | 9\58 | 186.21 | 10/9 | Secant |
| 2 | 17\58 (12\58) |
351.72 (248.28) |
11/9 (15/13) |
Sruti |
| 2 | 21\58 (8\58) |
434.48 (165.52) |
9/7 (11/10) |
Echidna |
| 2 | 24\58 (5\58) |
496.55 (103.45) |
4/3 (17/16) |
Diaschismic |
| 2 | 25\58 (4\58) |
517.24 (82.76) |
27/20 (21/20) |
Harry |
| 29 | 19\58 (1\58) |
393.10 (20.69) |
5/4 (91/90) |
Mystery |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
58et can also be detempered to semihemi (58 & 140), supers (58 & 152), condor (58 & 159), and eagle (58 & 212).
Scales
Instruments
- Lumatone mapping for 58edo
- 15\58 × 2\58 isomorphic instrument layout
- 15\58 × 4\58 isomorphic instrument layout
- 17\58 × 2\58 isomorphic instrument layout
Music
- 58edo improv (2025)
- We Wish You A Larry Christmas (2024) – larry in 58edo