5edo: Difference between revisions
→Theory: +subsets and supersets |
m →Intervals: Link to 1/1, misc. edits |
||
| Line 44: | Line 44: | ||
| 0 | | 0 | ||
| Unison (prime) | | Unison (prime) | ||
| 1/1 (just) | | [[1/1]] (just) | ||
| | | | ||
| | | | ||
| | | | ||
|[[File:0-0 unison.mp3|frameless]] | | [[File:0-0 unison.mp3|frameless]] | ||
|- | |- | ||
| 1 | | 1 | ||
| Line 57: | Line 57: | ||
| [[8/7]] (+8.826)<br>[[7/6]] (-26.871) | | [[8/7]] (+8.826)<br>[[7/6]] (-26.871) | ||
| [[224/195]] (-0.030) | | [[224/195]] (-0.030) | ||
|[[File:0-240 second, third (5-EDO).mp3|frameless]] | | [[File:0-240 second, third (5-EDO).mp3|frameless]] | ||
|- | |- | ||
| 2 | | 2 | ||
| Line 66: | Line 66: | ||
| [[33/25]] (-0.686) | | [[33/25]] (-0.686) | ||
| | | | ||
|[[File:0-480 fourth (5-EDO).mp3|frameless]] | | [[File:0-480 fourth (5-EDO).mp3|frameless]] | ||
|- | |- | ||
| 3 | | 3 | ||
| Line 75: | Line 75: | ||
| [[50/33]] (+0.686) | | [[50/33]] (+0.686) | ||
| | | | ||
|[[File:0-720 fifth (5-EDO).mp3|frameless]] | | [[File:0-720 fifth (5-EDO).mp3|frameless]] | ||
|- | |- | ||
| 4 | | 4 | ||
| Line 84: | Line 84: | ||
| [[12/7]] (+26.871)<br>[[7/4]] (-8.826) | | [[12/7]] (+26.871)<br>[[7/4]] (-8.826) | ||
| [[195/112]] (+0.030) | | [[195/112]] (+0.030) | ||
|[[File:0-960 sixth, seventh (5-EDO).mp3|frameless]] | | [[File:0-960 sixth, seventh (5-EDO).mp3|frameless]] | ||
|- | |- | ||
| 5 | | 5 | ||
| Line 93: | Line 93: | ||
| | | | ||
| | | | ||
|[[File:0-1200 octave.mp3|frameless]] | | [[File:0-1200 octave.mp3|frameless]] | ||
|} | |} | ||
Revision as of 08:40, 2 January 2024
| ← 4edo | 5edo | 6edo → |
(convergent)
5edo is notable for being the smallest edo containing xenharmonic intervals — 1edo, 2edo, 3edo, and 4edo are all subsets of 12edo.
Theory
If 5edo is regarded as a temperament, which is to say as 5tet, then the most salient fact is that 16/15 is tempered out. This means in 5tet the major third and the fourth, and the minor sixth and the fifth, are not distinguished; this is 5-limit father temperament.
Also tempered out is 27/25, if we temper this out in preference to 16/15 we obtain bug temperament, which equates 10/9 with 6/5: it is a little more perverse even than father. Because these intervals are so large, this sort of analysis is less significant with 5 than it becomes with larger and more accurate divisions, but it still plays a role. For example, I-IV-V-I is the same as I-III-V-I and involves triads with common intervals because of fourth-thirds equivalence.
Despite its lack of accuracy, 5edo is the second zeta integral edo, after 2edo. It also is the smallest equal division representing the 9-odd-limit consistently, giving a distinct value modulo five to 1, 3, 5, 7 and 9. Hence in a way similar to how 4edo can be used, and which is discussed in that article, it can be used to represent 7-limit intervals in terms of their position in a pentad, by giving a triple of integers representing a pentad in the lattice of tetrads/pentads together with the number of scale steps in 5edo. However, while 2edo represents the 3-odd-limit consistently, 3edo the 5-odd-limit, 4edo the 7-odd-limit and 5edo the 9-odd-limit, to represent the 11-odd-limit consistently with a patent val requires going all the way to 22edo. Nevertheless, because the comma tempered out for this edo's circle of fifths is 256/243, and since this interval is smaller than half a step, 5edo is the second edo to demonstrate 3-to-2 telicity — that is, when not counting the comparatively trivial 1edo.
In addition, considering 5edo as a no-5's temperament improves its standing significantly. It is especially prominent as a simple 2.3.7 temperament with high relative accuracy (the next edo doing it better being 17). It is the optimal patent val for the no-5s trienstonic (or Zo) temperament, although this is a very inaccurate temperament.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0 | +18 | +94 | -9 | -71 | +119 | -105 | -58 | +92 | -70 | +55 |
| Relative (%) | +0.0 | +7.5 | +39.0 | -3.7 | -29.7 | +49.8 | -43.7 | -24.0 | +38.2 | -29.0 | +22.9 | |
| Steps (reduced) |
5 (0) |
8 (3) |
12 (2) |
14 (4) |
17 (2) |
19 (4) |
20 (0) |
21 (1) |
23 (3) |
24 (4) |
25 (0) | |
Subsets and supersets
5edo is the 3rd prime edo, after 2edo and 3edo and before 7edo. Multiples such as 10edo, 15edo, … up to 35edo, share the same tuning of the perfect fifth as 5edo, while improving on other intervals.
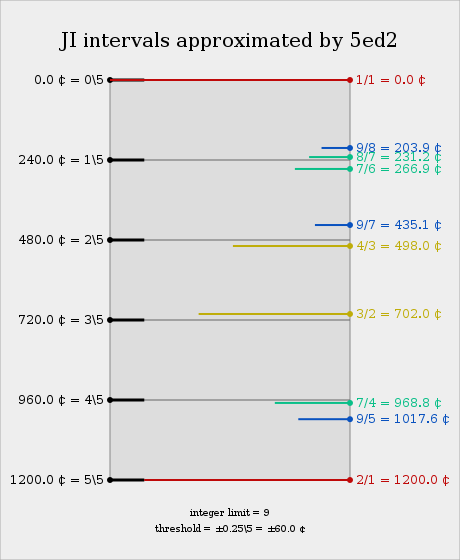
Intervals
| Degree | Cents | Interval region | Approximated JI intervals (error in ¢) | Audio | |||
|---|---|---|---|---|---|---|---|
| 3-limit | 5-limit | 7-limit | Other | ||||
| 0 | 0 | Unison (prime) | 1/1 (just) | ||||
| 1 | 240 | Supermajor second Inframinor third |
144/125 (-4.969) 125/108 (-13.076) |
8/7 (+8.826) 7/6 (-26.871) |
224/195 (-0.030) | ||
| 2 | 480 | Subfourth | 4/3 (-18.045) | 21/16 (+9.219) | 33/25 (-0.686) | ||
| 3 | 720 | Superfifth | 3/2 (+18.045) | 32/21 (-9.219) | 50/33 (+0.686) | ||
| 4 | 960 | Augmented sixth Subminor seventh |
216/125 (+13.076) 125/72 (+4.969) |
12/7 (+26.871) 7/4 (-8.826) |
195/112 (+0.030) | ||
| 5 | 1200 | Octave | 2/1 (just) | ||||
Notation
The usual notation system for 5edo is the chain-of-fifths notation, which is directly derived from the standard notation used in 12edo.
| Degree | Cents | Chain-of-fifths notation | |
|---|---|---|---|
| Diatonic interval names | Note names (on D) | ||
| 0 | 0 | Perfect unison (P1) Minor second (m2) Diminished third (d3) |
D Eb Fb |
| 1 | 240 | Augmented unison (A1) Major second (M2) Minor third (m3) Diminished fourth (d4) |
D# E F Gb |
| 2 | 480 | Augmented second (A2) Major third (M3) Perfect fourth (P4) Diminished fifth (d5) |
E# F# G Ab |
| 3 | 720 | Augmented fourth (A4) Perfect fifth (P5) Minor sixth (m6) Diminished seventh (d7) |
G# A Bb Cb |
| 4 | 960 | Augmented fifth (A5) Major sixth (M6) Minor seventh (m7) Diminished octave (d8) |
A# B C Db |
| 5 | 1200 | Augmented sixth (A6) Major seventh (M7) Perfect octave (P8) |
B# C# D |
In 5edo:
- ups and downs notation is identical to circle-of-fifths notation;
- mixed sagittal notation is identical to circle-of-fifths notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp (
 ) and sagittal flat (
) and sagittal flat ( ) respectively.
) respectively.
Alternative notations
- via Reinhard's cents notation
- a four-line hybrid treble/bass staff.
Intervals can be named penta-2nd, penta-3rd, penta-4th, penta-5th and octave.
Kite Giedraitis has proposed pentatonic interval names that retain the appearance of heptatonic names, to avoid the confusion caused by one's lifelong association of "fourth" with 4/3, not 3/2. The interval names are unisoid, subthird, fourthoid, fifthoid, subseventh and octoid, or 1d s3 4d 5d s7 8d. When notating larger edos such as 8 or 13, there are major or minor sub3rds and sub7ths. Note that 15/8 is an octoid.
For note names, Kite omits B and merges E and F into a new letter, "eef" (rhymes with leaf). Eef, like E, is a 5th above A. Eef, like F, is a 4th above C. The circle of 5ths is C G D A Eef C. Eef is written like an E, but with the bottom horizontal line going not right but left from the vertical line. Eef can be typed as ꘙ (unicode A619) or ⊧ (unicode 22A7). Eef can also be used to notate 15edo.
Solfege
| Degree | Cents | Standard solfege (movable do) |
Uniform solfege (1 vowel) |
|---|---|---|---|
| 0 | 0 | Do (P1) | Da (P1) |
| 1 | 240 | Re (M2) Me (m3) |
Ra (M2) Na (m3) |
| 2 | 480 | Mi (M3) Fa (P4) |
Ma (M3) Fa (P4) |
| 3 | 720 | So (P5) Le (m6) |
Sa (P5) Fla (m6) |
| 4 | 960 | La (M6) Te (m7) |
La (M6) Tha (m7) |
| 5 | 1200 | Ti (M7) Do (P8) |
Da (P8) |
JI approximation
Selected 7-limit intervals
Observations
Related scales
- By its cardinality, 5edo is related to other pentatonic scales, and it is especially close in sound to many Indonesian slendros.
- Due to the interest around the "fifth" interval size, there are many nonoctave "stretch sisters" to 5edo: square root of 4/3, cube root of 3/2, 8th root of 3, etc.
- For the same reason there are many "circle sisters":
- Make a chain of five "bigger fifths" (50/33), which makes three octaves 3.227¢ flat. (50/33)^5 = 7.985099.
Cycles, divisions
5 is a prime number so 5edo contains no sub-edos. Only simple cycles:
- Cycle of seconds: 0-1-2-3-4-0
- Cycle of fourths: 0-2-4-1-3-0
- Cycle of fifths: 0-3-1-4-2-0
- Cycle of sevenths: 0-4-3-2-1-0
Harmony
5edo does not have any strong consonance nor dissonance. The 240 cent interval can serve as either a major second or minor third, and the 960 cent interval as either a major sixth or minor seventh. The fourth is about 18 cents flat of a just fourth, making it rather "dirty" but recognizable. The fifth is likewise about 18 cents sharp of a just fifth, dissonant but still easily recognizable.
In contrast to other edos, all of the notes can be used at once in order to get a functioning scale. (As in Blackwood in 10edo).
Important chords:
- 0+1+3
- 0+2+3
- 0+1+3+4
- 0+2+3+4
Melody
Smallest edo that can be used for melodies in a "standard" way. The relatively large step of 240 cents can be used as major second for the melody construction. The scale has whole-tone as well as pentatonic character.
Chord or scale?
Either way, it is hard to wander very far from where you start. However, it has the scale-like feature that there are (barely) enough notes to create melody, in the form of an equal version of pentatonic.
Regular temperament properties
Uniform maps
Lua error in Module:Uniform_map at line 135: Must provide edo if not min or max given..
Commas
5edo tempers out the following commas. This assumes the val ⟨5 8 12 14 17 19].
| Prime Limit |
Ratio[note 1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 256/243 | [8 -5⟩ | 90.225 | Sawa | Limma, Pythagorean diatonic semitone |
| 5 | 27/25 | [0 3 -2⟩ | 133.238 | Gugu | Large limma |
| 5 | 16/15 | [4 -1 -1⟩ | 111.731 | Gubi | Classic diatonic semitone |
| 5 | 81/80 | [-4 4 -1⟩ | 21.506 | Gu | Syntonic comma, Didymus comma, meantone comma |
| 5 | (22 digits) | [24 -21 4⟩ | 4.200 | Sasa-quadyo | Vulture |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.770 | Rugu | Septimal quarter tone |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.697 | Zozo | Slendro diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.264 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | 245/243 | [0 -5 1 2⟩ | 14.191 | Zozoyo | Sensamagic |
| 7 | 1728/1715 | [6 3 -1 -3⟩ | 13.074 | Triru-agu | Orwellisma, Orwell comma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.433 | Latrizo | Gamelisma |
| 7 | 19683/19600 | [-4 9 -2 -2⟩ | 7.316 | Labiruru | Cataharry |
| 7 | 5120/5103 | [10 -6 1 -1⟩ | 5.758 | Saruyo | Hemifamity |
| 7 | (18 digits) | [-26 -1 1 9⟩ | 3.792 | Latritrizo-ayo | Wadisma |
| 7 | (12 digits) | [-6 -8 2 5⟩ | 1.117 | Quinzo-ayoyo | Wizma |
| 11 | 11/10 | [-1 0 -1 0 1⟩ | 165.004 | Logu | Large undecimal neutral 2nd |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.576 | Loruru | Mothwellsma |
| 11 | 896/891 | [7 -4 0 1 -1⟩ | 9.688 | Saluzo | Pentacircle |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.503 | Lozoyo | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.930 | Luzozogu | Werckisma |
| 11 | 3025/3024 | [-4 -3 2 -1 2⟩ | 0.572 | Loloruyoyo | Lehmerisma |
| 13 | 14/13 | [1 0 0 1 0 -1⟩ | 128.298 | Thuzo | Tridecimal 2/3-tone, trienthird |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.130 | Thozogu | Superleap |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.563 | Bithogu | Island comma, parizeksma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Ear training
5edo ear-training exercises by Alex Ness available here:
For any musician, there is no substitute for the experience of a particular xenharmonic sound. The user going by the name Hyacinth on Wikipedia and Wikimedia Commons has many xenharmonic MIDI's and has graciously copylefted them! This is his 5-TET scale MIDI:
Music
- See also: Category:5edo tracks
- Dmitry Bazhenov
- Hey, ule! (1st and 3rd sections) (Youtube) (2020)
- River flowing (Boris Tchaikovsky 5edo transcription) (2023, original piece from cycle Pentatonic composed in 1993)
- 5 EDO Ukulele (2011)
- something minimalistic idk (2022)
- Flight of the Bumblebee in 5edo (2023)
- Like japanese curry (2020)
- Like a calm river flow (2022)
- "Prelude in 5ET", from The Equal-Tempered Keyboard (1999-2022) (SoundCloud)
- "Invention in 5ET", from The Equal-Tempered Keyboard (1999-2022) (SoundCloud)
- Vince Kaichan
- "Ether", from STAFFcirc vol. 7 (2021) (Bandcamp)
Various and sundry
- Daybreak (2000)
- NullPointerException Music
- Frontier (2020)
- "Winter Forest", from Edolian (2020)
- Paul Rubenstein
Various, with electric guitars in 10edo and 15edo
- Sleeping Through It All (2004)
- 5-tet funk (2004)
- Pentacle (2004)
- "Garden of Light", from Formless Shadows (2021)
- Asîmchômsaia (2007)
- Slendronica#1b (2009)
There is also much 5edo-like world music, just search for "gyil" or "amadinda" or "slendro".