List of MOS scales in 37edo

From Xenharmonic Wiki
(Redirected from MOS Scales of 37edo)
Jump to navigation Jump to search

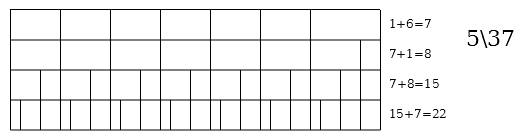
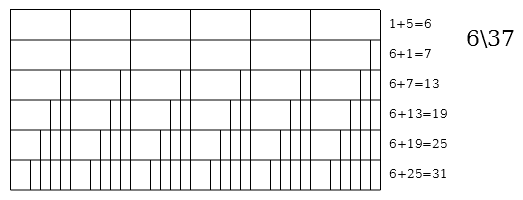
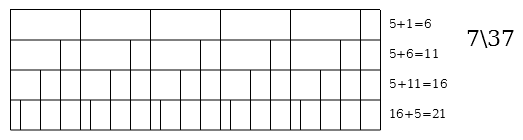
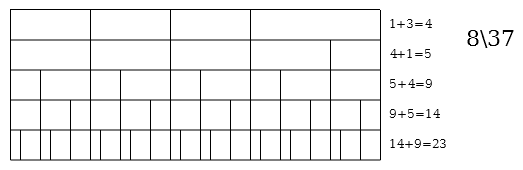
This page lists all moment of symmetry scales in 37edo.

Single-period MOS scales

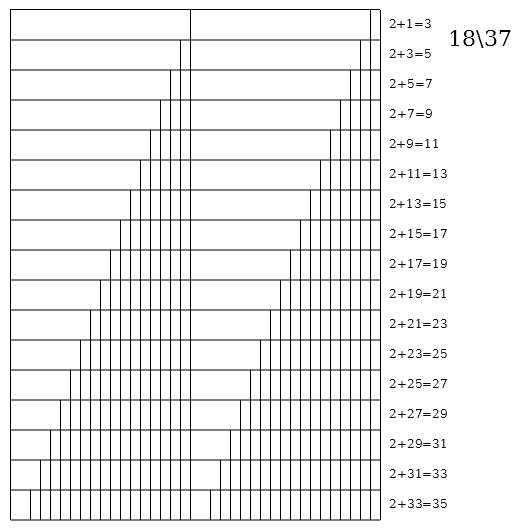
Generators 19\37 and 18\37
Step visualization MOS (name) Step sizes Step ratio
├──────────────────┼─────────────────┤ 1L 1s 19, 18 19:18
├┼─────────────────┼─────────────────┤ 2L 1s 18, 1 18:1
├┼┼────────────────┼┼────────────────┤ 2L 3s 17, 1 17:1
├┼┼┼───────────────┼┼┼───────────────┤ 2L 5s (antidiatonic) 16, 1 16:1
├┼┼┼┼──────────────┼┼┼┼──────────────┤ 2L 7s (balzano) 15, 1 15:1
├┼┼┼┼┼─────────────┼┼┼┼┼─────────────┤ 2L 9s 14, 1 14:1
├┼┼┼┼┼┼────────────┼┼┼┼┼┼────────────┤ 2L 11s 13, 1 13:1
├┼┼┼┼┼┼┼───────────┼┼┼┼┼┼┼───────────┤ 2L 13s 12, 1 12:1
├┼┼┼┼┼┼┼┼──────────┼┼┼┼┼┼┼┼──────────┤ 2L 15s 11, 1 11:1
├┼┼┼┼┼┼┼┼┼─────────┼┼┼┼┼┼┼┼┼─────────┤ 2L 17s 10, 1 10:1
├┼┼┼┼┼┼┼┼┼┼────────┼┼┼┼┼┼┼┼┼┼────────┤ 2L 19s 9, 1 9:1
├┼┼┼┼┼┼┼┼┼┼┼───────┼┼┼┼┼┼┼┼┼┼┼───────┤ 2L 21s 8, 1 8:1
├┼┼┼┼┼┼┼┼┼┼┼┼──────┼┼┼┼┼┼┼┼┼┼┼┼──────┤ 2L 23s 7, 1 7:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼─────┼┼┼┼┼┼┼┼┼┼┼┼┼─────┤ 2L 25s 6, 1 6:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼────┼┼┼┼┼┼┼┼┼┼┼┼┼┼────┤ 2L 27s 5, 1 5:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼───┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼───┤ 2L 29s 4, 1 4:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼──┤ 2L 31s 3, 1 3:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼─┤ 2L 33s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
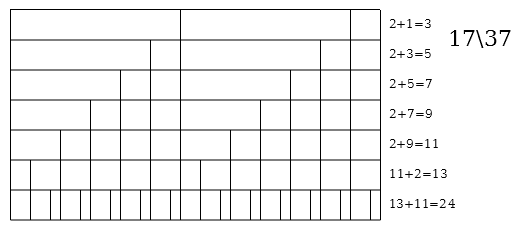
Generators 20\37 and 17\37
Step visualization MOS (name) Step sizes Step ratio
├───────────────────┼────────────────┤ 1L 1s 20, 17 20:17
├──┼────────────────┼────────────────┤ 2L 1s 17, 3 17:3
├──┼──┼─────────────┼──┼─────────────┤ 2L 3s 14, 3 14:3
├──┼──┼──┼──────────┼──┼──┼──────────┤ 2L 5s (antidiatonic) 11, 3 11:3
├──┼──┼──┼──┼───────┼──┼──┼──┼───────┤ 2L 7s (balzano) 8, 3 8:3
├──┼──┼──┼──┼──┼────┼──┼──┼──┼──┼────┤ 2L 9s 5, 3 5:3
├──┼──┼──┼──┼──┼──┼─┼──┼──┼──┼──┼──┼─┤ 11L 2s 3, 2 3:2
├┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼─┤ 13L 11s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 21\37 and 16\37
Step visualization MOS (name) Step sizes Step ratio
├────────────────────┼───────────────┤ 1L 1s 21, 16 21:16
├────┼───────────────┼───────────────┤ 2L 1s 16, 5 16:5
├────┼────┼──────────┼────┼──────────┤ 2L 3s 11, 5 11:5
├────┼────┼────┼─────┼────┼────┼─────┤ 2L 5s (antidiatonic) 6, 5 6:5
├────┼────┼────┼────┼┼────┼────┼────┼┤ 7L 2s (armotonic) 5, 1 5:1
├───┼┼───┼┼───┼┼───┼┼┼───┼┼───┼┼───┼┼┤ 7L 9s 4, 1 4:1
├──┼┼┼──┼┼┼──┼┼┼──┼┼┼┼──┼┼┼──┼┼┼──┼┼┼┤ 7L 16s 3, 1 3:1
├─┼┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼┼┤ 7L 23s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 22\37 and 15\37
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────┼──────────────┤ 1L 1s 22, 15 22:15
├──────┼──────────────┼──────────────┤ 2L 1s 15, 7 15:7
├──────┼──────┼───────┼──────┼───────┤ 2L 3s 8, 7 8:7
├──────┼──────┼──────┼┼──────┼──────┼┤ 5L 2s (diatonic) 7, 1 7:1
├─────┼┼─────┼┼─────┼┼┼─────┼┼─────┼┼┤ 5L 7s 6, 1 6:1
├────┼┼┼────┼┼┼────┼┼┼┼────┼┼┼────┼┼┼┤ 5L 12s 5, 1 5:1
├───┼┼┼┼───┼┼┼┼───┼┼┼┼┼───┼┼┼┼───┼┼┼┼┤ 5L 17s 4, 1 4:1
├──┼┼┼┼┼──┼┼┼┼┼──┼┼┼┼┼┼──┼┼┼┼┼──┼┼┼┼┼┤ 5L 22s 3, 1 3:1
├─┼┼┼┼┼┼─┼┼┼┼┼┼─┼┼┼┼┼┼┼─┼┼┼┼┼┼─┼┼┼┼┼┼┤ 5L 27s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 23\37 and 14\37
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────┼─────────────┤ 1L 1s 23, 14 23:14
├────────┼─────────────┼─────────────┤ 2L 1s 14, 9 14:9
├────────┼────────┼────┼────────┼────┤ 3L 2s 9, 5 9:5
├───┼────┼───┼────┼────┼───┼────┼────┤ 5L 3s (oneirotonic) 5, 4 5:4
├───┼───┼┼───┼───┼┼───┼┼───┼───┼┼───┼┤ 8L 5s 4, 1 4:1
├──┼┼──┼┼┼──┼┼──┼┼┼──┼┼┼──┼┼──┼┼┼──┼┼┤ 8L 13s 3, 1 3:1
├─┼┼┼─┼┼┼┼─┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼─┼┼┼┼─┼┼┼┤ 8L 21s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 24\37 and 13\37
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────┼────────────┤ 1L 1s 24, 13 24:13
├──────────┼────────────┼────────────┤ 2L 1s 13, 11 13:11
├──────────┼──────────┼─┼──────────┼─┤ 3L 2s 11, 2 11:2
├────────┼─┼────────┼─┼─┼────────┼─┼─┤ 3L 5s (checkertonic) 9, 2 9:2
├──────┼─┼─┼──────┼─┼─┼─┼──────┼─┼─┼─┤ 3L 8s 7, 2 7:2
├────┼─┼─┼─┼────┼─┼─┼─┼─┼────┼─┼─┼─┼─┤ 3L 11s 5, 2 5:2
├──┼─┼─┼─┼─┼──┼─┼─┼─┼─┼─┼──┼─┼─┼─┼─┼─┤ 3L 14s 3, 2 3:2
├┼─┼─┼─┼─┼─┼┼─┼─┼─┼─┼─┼─┼┼─┼─┼─┼─┼─┼─┤ 17L 3s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 25\37 and 12\37
Step visualization MOS (name) Step sizes Step ratio
├────────────────────────┼───────────┤ 1L 1s 25, 12 25:12
├────────────┼───────────┼───────────┤ 1L 2s 13, 12 13:12
├┼───────────┼───────────┼───────────┤ 3L 1s 12, 1 12:1
├┼┼──────────┼┼──────────┼┼──────────┤ 3L 4s (mosh) 11, 1 11:1
├┼┼┼─────────┼┼┼─────────┼┼┼─────────┤ 3L 7s (sephiroid) 10, 1 10:1
├┼┼┼┼────────┼┼┼┼────────┼┼┼┼────────┤ 3L 10s 9, 1 9:1
├┼┼┼┼┼───────┼┼┼┼┼───────┼┼┼┼┼───────┤ 3L 13s 8, 1 8:1
├┼┼┼┼┼┼──────┼┼┼┼┼┼──────┼┼┼┼┼┼──────┤ 3L 16s 7, 1 7:1
├┼┼┼┼┼┼┼─────┼┼┼┼┼┼┼─────┼┼┼┼┼┼┼─────┤ 3L 19s 6, 1 6:1
├┼┼┼┼┼┼┼┼────┼┼┼┼┼┼┼┼────┼┼┼┼┼┼┼┼────┤ 3L 22s 5, 1 5:1
├┼┼┼┼┼┼┼┼┼───┼┼┼┼┼┼┼┼┼───┼┼┼┼┼┼┼┼┼───┤ 3L 25s 4, 1 4:1
├┼┼┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼┼┼──┤ 3L 28s 3, 1 3:1
├┼┼┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼┼┼─┤ 3L 31s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 26\37 and 11\37
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────────┼──────────┤ 1L 1s 26, 11 26:11
├──────────────┼──────────┼──────────┤ 1L 2s 15, 11 15:11
├───┼──────────┼──────────┼──────────┤ 3L 1s 11, 4 11:4
├───┼───┼──────┼───┼──────┼───┼──────┤ 3L 4s (mosh) 7, 4 7:4
├───┼───┼───┼──┼───┼───┼──┼───┼───┼──┤ 7L 3s (dicoid) 4, 3 4:3
├┼──┼┼──┼┼──┼──┼┼──┼┼──┼──┼┼──┼┼──┼──┤ 10L 7s 3, 1 3:1
├┼┼─┼┼┼─┼┼┼─┼┼─┼┼┼─┼┼┼─┼┼─┼┼┼─┼┼┼─┼┼─┤ 10L 17s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 27\37 and 10\37
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────────┼─────────┤ 1L 1s 27, 10 27:10
├────────────────┼─────────┼─────────┤ 1L 2s 17, 10 17:10
├──────┼─────────┼─────────┼─────────┤ 3L 1s 10, 7 10:7
├──────┼──────┼──┼──────┼──┼──────┼──┤ 4L 3s (smitonic) 7, 3 7:3
├───┼──┼───┼──┼──┼───┼──┼──┼───┼──┼──┤ 4L 7s 4, 3 4:3
├┼──┼──┼┼──┼──┼──┼┼──┼──┼──┼┼──┼──┼──┤ 11L 4s 3, 1 3:1
├┼┼─┼┼─┼┼┼─┼┼─┼┼─┼┼┼─┼┼─┼┼─┼┼┼─┼┼─┼┼─┤ 11L 15s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 28\37 and 9\37
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────────┼────────┤ 1L 1s 28, 9 28:9
├──────────────────┼────────┼────────┤ 1L 2s 19, 9 19:9
├─────────┼────────┼────────┼────────┤ 1L 3s 10, 9 10:9
├┼────────┼────────┼────────┼────────┤ 4L 1s 9, 1 9:1
├┼┼───────┼┼───────┼┼───────┼┼───────┤ 4L 5s (gramitonic) 8, 1 8:1
├┼┼┼──────┼┼┼──────┼┼┼──────┼┼┼──────┤ 4L 9s 7, 1 7:1
├┼┼┼┼─────┼┼┼┼─────┼┼┼┼─────┼┼┼┼─────┤ 4L 13s 6, 1 6:1
├┼┼┼┼┼────┼┼┼┼┼────┼┼┼┼┼────┼┼┼┼┼────┤ 4L 17s 5, 1 5:1
├┼┼┼┼┼┼───┼┼┼┼┼┼───┼┼┼┼┼┼───┼┼┼┼┼┼───┤ 4L 21s 4, 1 4:1
├┼┼┼┼┼┼┼──┼┼┼┼┼┼┼──┼┼┼┼┼┼┼──┼┼┼┼┼┼┼──┤ 4L 25s 3, 1 3:1
├┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼─┤ 4L 29s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
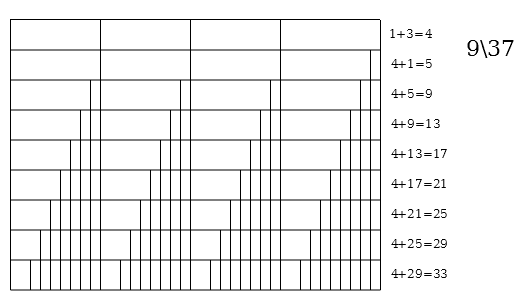
Generators 29\37 and 8\37
Step visualization MOS (name) Step sizes Step ratio
├────────────────────────────┼───────┤ 1L 1s 29, 8 29:8
├────────────────────┼───────┼───────┤ 1L 2s 21, 8 21:8
├────────────┼───────┼───────┼───────┤ 1L 3s 13, 8 13:8
├────┼───────┼───────┼───────┼───────┤ 4L 1s 8, 5 8:5
├────┼────┼──┼────┼──┼────┼──┼────┼──┤ 5L 4s (semiquartal) 5, 3 5:3
├─┼──┼─┼──┼──┼─┼──┼──┼─┼──┼──┼─┼──┼──┤ 9L 5s 3, 2 3:2
├─┼─┼┼─┼─┼┼─┼┼─┼─┼┼─┼┼─┼─┼┼─┼┼─┼─┼┼─┼┤ 14L 9s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
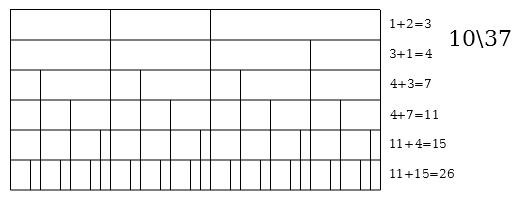
Generators 30\37 and 7\37
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────────────┼──────┤ 1L 1s 30, 7 30:7
├──────────────────────┼──────┼──────┤ 1L 2s 23, 7 23:7
├───────────────┼──────┼──────┼──────┤ 1L 3s 16, 7 16:7
├────────┼──────┼──────┼──────┼──────┤ 1L 4s 9, 7 9:7
├─┼──────┼──────┼──────┼──────┼──────┤ 5L 1s (machinoid) 7, 2 7:2
├─┼─┼────┼─┼────┼─┼────┼─┼────┼─┼────┤ 5L 6s 5, 2 5:2
├─┼─┼─┼──┼─┼─┼──┼─┼─┼──┼─┼─┼──┼─┼─┼──┤ 5L 11s 3, 2 3:2
├─┼─┼─┼─┼┼─┼─┼─┼┼─┼─┼─┼┼─┼─┼─┼┼─┼─┼─┼┤ 16L 5s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
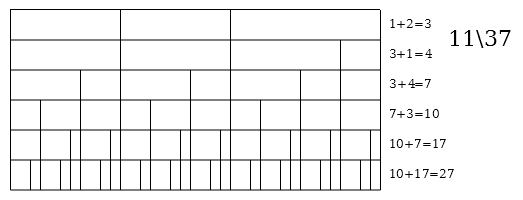
Generators 31\37 and 6\37
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────────────┼─────┤ 1L 1s 31, 6 31:6
├────────────────────────┼─────┼─────┤ 1L 2s 25, 6 25:6
├──────────────────┼─────┼─────┼─────┤ 1L 3s 19, 6 19:6
├────────────┼─────┼─────┼─────┼─────┤ 1L 4s 13, 6 13:6
├──────┼─────┼─────┼─────┼─────┼─────┤ 1L 5s (antimachinoid) 7, 6 7:6
├┼─────┼─────┼─────┼─────┼─────┼─────┤ 6L 1s (archaeotonic) 6, 1 6:1
├┼┼────┼┼────┼┼────┼┼────┼┼────┼┼────┤ 6L 7s 5, 1 5:1
├┼┼┼───┼┼┼───┼┼┼───┼┼┼───┼┼┼───┼┼┼───┤ 6L 13s 4, 1 4:1
├┼┼┼┼──┼┼┼┼──┼┼┼┼──┼┼┼┼──┼┼┼┼──┼┼┼┼──┤ 6L 19s 3, 1 3:1
├┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┤ 6L 25s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 32\37 and 5\37
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────────────┼────┤ 1L 1s 32, 5 32:5
├──────────────────────────┼────┼────┤ 1L 2s 27, 5 27:5
├─────────────────────┼────┼────┼────┤ 1L 3s 22, 5 22:5
├────────────────┼────┼────┼────┼────┤ 1L 4s 17, 5 17:5
├───────────┼────┼────┼────┼────┼────┤ 1L 5s (antimachinoid) 12, 5 12:5
├──────┼────┼────┼────┼────┼────┼────┤ 1L 6s (onyx) 7, 5 7:5
├─┼────┼────┼────┼────┼────┼────┼────┤ 7L 1s (pine) 5, 2 5:2
├─┼─┼──┼─┼──┼─┼──┼─┼──┼─┼──┼─┼──┼─┼──┤ 7L 8s 3, 2 3:2
├─┼─┼─┼┼─┼─┼┼─┼─┼┼─┼─┼┼─┼─┼┼─┼─┼┼─┼─┼┤ 15L 7s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 33\37 and 4\37
Step visualization MOS (name) Step sizes Step ratio
├────────────────────────────────┼───┤ 1L 1s 33, 4 33:4
├────────────────────────────┼───┼───┤ 1L 2s 29, 4 29:4
├────────────────────────┼───┼───┼───┤ 1L 3s 25, 4 25:4
├────────────────────┼───┼───┼───┼───┤ 1L 4s 21, 4 21:4
├────────────────┼───┼───┼───┼───┼───┤ 1L 5s (antimachinoid) 17, 4 17:4
├────────────┼───┼───┼───┼───┼───┼───┤ 1L 6s (onyx) 13, 4 13:4
├────────┼───┼───┼───┼───┼───┼───┼───┤ 1L 7s (antipine) 9, 4 9:4
├────┼───┼───┼───┼───┼───┼───┼───┼───┤ 1L 8s (antisubneutralic) 5, 4 5:4
├┼───┼───┼───┼───┼───┼───┼───┼───┼───┤ 9L 1s (sinatonic) 4, 1 4:1
├┼┼──┼┼──┼┼──┼┼──┼┼──┼┼──┼┼──┼┼──┼┼──┤ 9L 10s 3, 1 3:1
├┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┤ 9L 19s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 34\37 and 3\37
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────────────────┼──┤ 1L 1s 34, 3 34:3
├──────────────────────────────┼──┼──┤ 1L 2s 31, 3 31:3
├───────────────────────────┼──┼──┼──┤ 1L 3s 28, 3 28:3
├────────────────────────┼──┼──┼──┼──┤ 1L 4s 25, 3 25:3
├─────────────────────┼──┼──┼──┼──┼──┤ 1L 5s (antimachinoid) 22, 3 22:3
├──────────────────┼──┼──┼──┼──┼──┼──┤ 1L 6s (onyx) 19, 3 19:3
├───────────────┼──┼──┼──┼──┼──┼──┼──┤ 1L 7s (antipine) 16, 3 16:3
├────────────┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 8s (antisubneutralic) 13, 3 13:3
├─────────┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 9s (antisinatonic) 10, 3 10:3
├──────┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 10s 7, 3 7:3
├───┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 11s 4, 3 4:3
├┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 12L 1s 3, 1 3:1
├┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┤ 12L 13s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 35\37 and 2\37
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────────────────┼─┤ 1L 1s 35, 2 35:2
├────────────────────────────────┼─┼─┤ 1L 2s 33, 2 33:2
├──────────────────────────────┼─┼─┼─┤ 1L 3s 31, 2 31:2
├────────────────────────────┼─┼─┼─┼─┤ 1L 4s 29, 2 29:2
├──────────────────────────┼─┼─┼─┼─┼─┤ 1L 5s (antimachinoid) 27, 2 27:2
├────────────────────────┼─┼─┼─┼─┼─┼─┤ 1L 6s (onyx) 25, 2 25:2
├──────────────────────┼─┼─┼─┼─┼─┼─┼─┤ 1L 7s (antipine) 23, 2 23:2
├────────────────────┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 8s (antisubneutralic) 21, 2 21:2
├──────────────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 9s (antisinatonic) 19, 2 19:2
├────────────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 10s 17, 2 17:2
├──────────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 11s 15, 2 15:2
├────────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 12s 13, 2 13:2
├──────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 13s 11, 2 11:2
├────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 14s 9, 2 9:2
├──────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 15s 7, 2 7:2
├────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 16s 5, 2 5:2
├──┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 17s 3, 2 3:2
├┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 18L 1s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1
Generators 36\37 and 1\37
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────────────────┼┤ 1L 1s 36, 1 36:1
├──────────────────────────────────┼┼┤ 1L 2s 35, 1 35:1
├─────────────────────────────────┼┼┼┤ 1L 3s 34, 1 34:1
├────────────────────────────────┼┼┼┼┤ 1L 4s 33, 1 33:1
├───────────────────────────────┼┼┼┼┼┤ 1L 5s (antimachinoid) 32, 1 32:1
├──────────────────────────────┼┼┼┼┼┼┤ 1L 6s (onyx) 31, 1 31:1
├─────────────────────────────┼┼┼┼┼┼┼┤ 1L 7s (antipine) 30, 1 30:1
├────────────────────────────┼┼┼┼┼┼┼┼┤ 1L 8s (antisubneutralic) 29, 1 29:1
├───────────────────────────┼┼┼┼┼┼┼┼┼┤ 1L 9s (antisinatonic) 28, 1 28:1
├──────────────────────────┼┼┼┼┼┼┼┼┼┼┤ 1L 10s 27, 1 27:1
├─────────────────────────┼┼┼┼┼┼┼┼┼┼┼┤ 1L 11s 26, 1 26:1
├────────────────────────┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 12s 25, 1 25:1
├───────────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 13s 24, 1 24:1
├──────────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 14s 23, 1 23:1
├─────────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 15s 22, 1 22:1
├────────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 16s 21, 1 21:1
├───────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 17s 20, 1 20:1
├──────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 18s 19, 1 19:1
├─────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 19s 18, 1 18:1
├────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 20s 17, 1 17:1
├───────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 21s 16, 1 16:1
├──────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 22s 15, 1 15:1
├─────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 23s 14, 1 14:1
├────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 24s 13, 1 13:1
├───────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 25s 12, 1 12:1
├──────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 26s 11, 1 11:1
├─────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 27s 10, 1 10:1
├────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 28s 9, 1 9:1
├───────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 29s 8, 1 8:1
├──────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 30s 7, 1 7:1
├─────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 31s 6, 1 6:1
├────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 32s 5, 1 5:1
├───┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 33s 4, 1 4:1
├──┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 34s 3, 1 3:1
├─┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 35s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 37edo 1, 1 1:1

37edo_mos_02.png

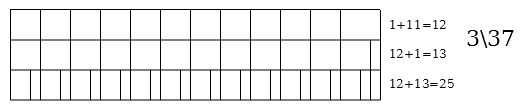
37edo_mos_03.png

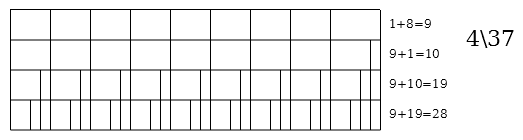37edo_mos_04.png.

37edo_mos_05.png

37edo_mos_06.png

37edo_mos_07.png

37edo_mos_08.png

37edo_mos_09.png

37edo_mos_10.png

37edo_mos_11.png

37edo_mos_12.png

37edo_mos_13.png

37edo_mos_14.png

37edo_mos_15.png

37edo_mos_16.png

37edo_mos_17.png

37edo_mos_18.png

Retrieved from "https://en.xen.wiki/index.php?title=List_of_MOS_scales_in_37edo&oldid=128768"