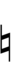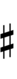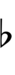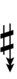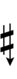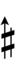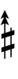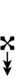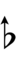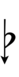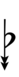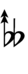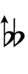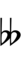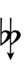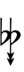39edo
| ← 38edo | 39edo | 40edo → |
39 equal divisions of the octave (abbreviated 39edo or 39ed2), also called 39-tone equal temperament (39tet) or 39 equal temperament (39et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 39 equal parts of about 30.8 ¢ each. Each step represents a frequency ratio of 21/39, or the 39th root of 2.
Theory
39edo's perfect fifth is 5.8 ¢ sharp. Together with its best classical major third which is the familiar 400 ¢ of 12edo, we get a system which tempers out the diesis (128/125) and the amity comma (1600000/1594323). We have two choices for a map for 7, but the sharp one works better with the 3 and 5, which adds 64/63 and 126/125 to the list. Tempering out both 128/125 and 64/63 makes 39et, in some few ways, allied to 12et in supporting augene, and is in fact, an excellent choice for an augene tuning, but one difference is that 39et has a fine 11, and adding it to consideration we find that the equal temperament tempers out 99/98 and 121/120 also. This choice for 39et is the 39d val ⟨39 62 91 110 135].
A particular anecdote with this system was made in the Teliochordon, in 1788 by Charles Clagget (Ireland, 1740?–1820), a little extract here.
As a superpyth system, 39edo is intermediate between 17edo and 22edo (39 = 17 + 22); its fifth thus falls in the "shrub region" where the diatonic thirds are between standard neogothic thirds and septimal thirds. The specific 7-limit variant supported by 39et is quasisuper. While 17edo is superb for melody (as documented by George Secor), it does not approximate the 5th harmonic at all and only poorly approximates the 7th. 22edo is much better for 5-limit and 7-limit harmony but is less effective for melody because the diatonic semitone is quartertone-sized, which results in a very strange-sounding diatonic scale. 39edo offers a compromise, since it still supports good 5- and 7-limit harmonies (though less close than 22edo), while at the same time having a diatonic semitone of 61.5 cents, as the ideal diatonic semitone for melody is somewhere in between 60 and 80 cents, i.e. a third tone, by Secor's estimates.
Alternatively, if we take 22\39 as a fifth, 39edo can be used as a tuning of mavila, and from that point of view it seems to have attracted the attention of the Armodue school, an Italian group that use the scheme of superdiatonic LLLsLLLLs like a base scale for notation and theory, suited in 16edo, and allied systems: 25edo [1/3-tone 3;2]; 41edo [1/5-tone 5;3]; and 57edo [1/7-tone 7;4]. The hornbostel temperament is included too with: 23edo [1/3-tone 3;1]; 39edo [1/5-tone 5;2] & 62edo [1/8-tone 8;3]. The mavila fifth in 39edo like all mavila fifths is very, very flat, in this case, 25 ¢ flat.
39edo offers not one, but many, possible ways of extending tonality beyond the diatonic scale, even if it does not do as good of a job at approximating JI as some other systems do. Because it can also approximate mavila as well as "anti-mavila" (oneirotonic), the latter of which it inherits from 13edo, this makes 39edo an extremely versatile temperament usable in a wide range of situations (both harmonic and inharmonic).
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +5.7 | +13.7 | -15.0 | +11.5 | +2.5 | -9.8 | -11.3 | -12.6 | +10.2 | -9.2 | -12.9 |
| Relative (%) | +18.6 | +44.5 | -48.7 | +37.3 | +8.2 | -31.7 | -36.9 | -41.1 | +33.1 | -30.0 | -41.9 | |
| Steps (reduced) |
62 (23) |
91 (13) |
109 (31) |
124 (7) |
135 (18) |
144 (27) |
152 (35) |
159 (3) |
166 (10) |
171 (15) |
176 (20) | |
Subsets and supersets
Since 39 factors into 3 × 13, 39edo contains 3edo and 13edo as subsets. Multiplying 39edo by 2 yields 78edo, which corrects several harmonics.
Intervals
| Steps | Cents | Approximate ratios* | Ups and downs notation | Nearest just interval (Ratio, cents, error) | ||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1/1 | P1 | perfect unison | D | 1/1 | 0.00 | None |
| 1 | 30.8 | 36/35, 50/49, 55/54, 56/55, 81/80 | ^1, vm2 |
up unison, downminor 2nd |
^D, vEb |
57/56 | 30.64 | +0.1271 |
| 2 | 61.5 | 28/27, 33/32, 49/48 | m2 | minor 2nd | Eb | 29/28 | 60.75 | +0.7872 |
| 3 | 92.3 | 16/15, 21/20, 25/24 | ^m2 | upminor 2nd | ^Eb | 39/37 | 91.14 | +1.1691 |
| 4 | 123.1 | 15/14 | ^^m2 | dupminor 2nd | ^^Eb | 44/41 | 122.26 | +0.8214 |
| 5 | 153.8 | 11/10, 12/11 | vvM2 | dudmajor 2nd | vvE | 35/32 | 155.14 | -1.2934 |
| 6 | 184.6 | 10/9 | vM2 | downmajor 2nd | vE | 10/9 | 182.40 | +2.2117 |
| 7 | 215.4 | 9/8, 8/7 | M2 | major 2nd | E | 17/15 | 216.69 | -1.3021 |
| 8 | 246.2 | 81/70 | ^M2, vm3 |
upmajor 2nd, downminor 3rd |
^E, vF |
15/13 | 247.74 | -1.5873 |
| 9 | 276.9 | 7/6 | m3 | minor 3rd | F | 27/23 | 277.59 | -0.6676 |
| 10 | 307.7 | 6/5 | ^m3 | upminor 3rd | ^F | 43/36 | 307.61 | +0.0846 |
| 11 | 338.5 | 11/9 | ^^m3 | dupminor 3rd | ^^F | 17/14 | 336.13 | +2.3320 |
| 12 | 369.2 | 27/22 | vvM3 | dudmajor 3rd | vvF# | 26/21 | 369.75 | -0.5160 |
| 13 | 400.0 | 5/4 | vM3 | downmajor 3rd | vF# | 34/27 | 399.09 | +0.9096 |
| 14 | 430.8 | 9/7, 14/11 | M3 | major 3rd | F# | 41/32 | 429.06 | +1.7068 |
| 15 | 461.5 | 35/27 | v4 | down 4th | vG | 30/23 | 459.99 | +1.5441 |
| 16 | 492.3 | 4/3 | P4 | perfect 4th | G | 85/64 | 491.27 | +1.0386 |
| 17 | 523.1 | 27/20 | ^4 | up 4th | ^G | 23/17 | 523.32 | -0.2420 |
| 18 | 553.8 | 11/8 | ^^4 | dup 4th | ^^G | 11/8 | 551.32 | +2.5283 |
| 19 | 584.6 | 7/5 | vvA4, ^d5 |
dudaug 4th, updim 5th |
vvG#, ^Ab |
7/5 | 582.51 | +2.1032 |
| 20 | 615.4 | 10/7 | vA4, ^^d5 |
downaug 4th, dupdim 5th |
vG#, ^^Ab |
10/7 | 617.49 | -2.1032 |
| 21 | 646.2 | 16/11 | vv5 | dud 5th | vvA | 16/11 | 648.68 | -2.5283 |
| 22 | 676.9 | 40/27 | v5 | down 5th | vA | 34/23 | 676.68 | +0.2420 |
| 23 | 707.7 | 3/2 | P5 | perfect 5th | A | 128/85 | 708.73 | -1.0386 |
| 24 | 738.5 | 54/35 | ^5 | up 5th | A^ | 23/15 | 740.01 | -1.5441 |
| 25 | 769.2 | 11/7, 14/9 | m6 | minor 6th | Bb | 64/41 | 770.94 | -1.7068 |
| 26 | 800.0 | 8/5 | ^m6 | upminor 6th | ^Bb | 27/17 | 800.91 | -0.9096 |
| 27 | 830.8 | 44/27 | ^^m6 | dupminor 6th | ^^Bb | 21/13 | 830.25 | +0.5160 |
| 28 | 861.5 | 18/11 | vvM6 | dudmajor 6th | vvB | 28/17 | 863.87 | -2.3320 |
| 29 | 892.3 | 5/3 | vM6 | downmajor 6th | vB | 72/43 | 892.39 | -0.0846 |
| 30 | 923.1 | 12/7 | M6 | major 6th | B | 46/27 | 922.41 | +0.6676 |
| 31 | 953.8 | 140/81 | ^M6, vm7 |
upmajor 6th, downminor 7th |
^B, vC |
26/15 | 952.26 | +1.5873 |
| 32 | 984.6 | 7/4, 16/9 | m7 | minor 7th | C | 30/17 | 983.31 | +1.3021 |
| 33 | 1015.4 | 9/5 | ^m7 | upminor 7th | ^C | 9/5 | 1017.60 | -2.2117 |
| 34 | 1046.2 | 11/6, 20/11 | ^^m7 | dupminor 7th | ^^C | 64/35 | 1044.86 | +1.2934 |
| 35 | 1076.9 | 28/15 | vvM7 | dudmajor 7th | vvC# | 41/22 | 1077.74 | -0.8214 |
| 36 | 1107.7 | 15/8, 40/21, 48/25 | vM7 | downmajor 7th | vC# | 74/39 | 1108.86 | -1.1691 |
| 37 | 1138.5 | 27/14, 96/49, 64/33 | M7 | major 7th | C# | 56/29 | 1139.25 | -0.7872 |
| 38 | 1169.2 | 35/18, 49/25, 55/28, 108/55, 160/81 | ^M7, v8 |
upmajor 7th, down 8ve |
^C#, vD |
112/57 | 1169.36 | -0.1271 |
| 39 | 1200.0 | 2/1 | P8 | perfect 8ve | D | 2/1 | 1200.00 | None |
* 11-limit in the 39d val, inconsistent intervals in italic
Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and downs notation #Chords and chord progressions.
Notation
Ups and downs notation
39edo can be notated with ups and downs, spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Another notation uses alternative ups and downs. Here, this can be done using sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Sagittal notation
This notation uses the same sagittal sequence as 46edo.
Evo flavor

Revo flavor

Armodue notation
- Armodue nomenclature 5;2 relation
- ‡ = Semisharp (1/5-tone up)
- b = Flat (3/5-tone down)
- # = Sharp (3/5-tone up)
- v = Semiflat (1/5-tone down)
| # | Cents | Armodue notation | Associated ratios | |
|---|---|---|---|---|
| 0 | 0.0 | 1 | 1/1 | |
| 1 | 30.8 | 1‡ (9#) | ||
| 2 | 61.5 | 2b | ||
| 3 | 92.3 | 1# | ||
| 4 | 123.1 | 2v | ||
| 5 | 153.8 | 2 | 11/10~12/11 | |
| 6 | 184.6 | 2‡ | ||
| 7 | · | 215.4 | 3b | 8/7 |
| 8 | 246.2 | 2# | ||
| 9 | 276.9 | 3v | ||
| 10 | 307.7 | 3 | 6/5~7/6 | |
| 11 | 338.5 | 3‡ | ||
| 12 | · | 369.2 | 4b | 5/4 |
| 13 | 400.0 | 3# | ||
| 14 | 430.8 | 4v (5b) | ||
| 15 | 461.5 | 4 | ||
| 16 | 492.3 | 4‡ (5v) | ||
| 17 | · | 523.1 | 5 | 4/3~11/8 |
| 18 | 553.8 | 5‡ (4#) | ||
| 19 | 584.6 | 6b | 10/7 | |
| 20 | 615.4 | 5# | 7/5 | |
| 21 | 646.2 | 6v | ||
| 22 | · | 676.9 | 6 | 3/2~16/11 |
| 23 | 707.7 | 6‡ | ||
| 24 | 738.5 | 7b | ||
| 25 | 769.2 | 6# | ||
| 26 | 800.0 | 7v | ||
| 27 | · | 830.8 | 7 | 8/5 |
| 28 | 861.5 | 7‡ | ||
| 29 | 892.3 | 8b | 5/3~12/7 | |
| 30 | 923.1 | 7# | ||
| 31 | 953.8 | 8v | ||
| 32 | · | 984.6 | 8 | 7/4 |
| 33 | 1015.4 | 8‡ | ||
| 34 | 1046.2 | 9b | 11/6~20/11 | |
| 35 | 1076.9 | 8# | ||
| 36 | 1107.7 | 9v (1b) | ||
| 37 | 1138.5 | 9 | ||
| 38 | 1169.2 | 9‡ (1v) | ||
| 39 | ·· | 1200.0 | 1 | 2/1 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [62 -39⟩ | [⟨39 62]] | −1.81 | 1.81 | 5.88 |
| 2.3.5 | 128/125, 1594323/1562500 | [⟨39 62 91]] | −3.17 | 2.42 | 7.89 |
| 2.3.5.7 | 64/63, 126/125, 2430/2401 | [⟨39 62 91 110]] (39d) | −3.78 | 2.35 | 7.65 |
| 2.3.5.7.11 | 64/63, 99/98, 121/120, 126/125 | [⟨39 62 91 110 135]] (39d) | −3.17 | 2.43 | 7.91 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Temperament | Mos scales |
|---|---|---|---|---|
| 1 | 1\39 | 30.8 | ||
| 1 | 2\39 | 61.5 | Unicorn (39d) | 1L 18s, 19L 1s |
| 1 | 4\39 | 123.1 | Negri (39c) | 1L 8s, 9L 1s, 10L 9s, 10L 19s |
| 1 | 5\39 | 153.8 | 1L 6s, 7L 1s, 8L 7s, 8L 15s, 8L 23s | |
| 1 | 7\39 | 215.4 | Machine (39d) | 1L 4s, 5L 1s, 6L 5s, 11L 6s, 11L 17s |
| 1 | 8\39 | 246.2 | Immunity (39) / immunized (39d) | 4L 1s, 5L 4s, 5L 9s, 5L 14s, 5L 19s, 5L 24s, 5L 29s |
| 1 | 10\39 | 307.7 | Familia (39df) | 3L 1s, 4L 3s, 4L 7s, 4L 11s, 4L 15s, 4L 19s, 4L 23s, 4L 27s, 4L 31s |
| 1 | 11\39 | 338.5 | Amity (39) / accord (39d) | 3L 1s, 4L 3s, 7L 4s, 7L 11s, 7L 18s, 7L 25s |
| 1 | 14\39 | 430.8 | Hamity (39df) | 3L 2s, 3L 5s, 3L 8s, 11L 3s, 14L 11s |
| 1 | 16\39 | 492.3 | Quasisuper (39d) | 2L 3s, 5L 2s, 5L 7s, 5L 12s, 17L 5s |
| 1 | 17\39 | 523.1 | Mavila (39bc) | 2L 3s, 2L 5s, 7L 2s, 7L 9s, 16L 7s |
| 1 | 19\39 | 584.6 | Pluto (39d) | 2L 3s, 2L 5s, 2L 7s, 2L 9s, 2L 11s, 2L 13s etc. … 2L 35s |
| 3 | 1\39 | 30.8 | ||
| 3 | 2\39 | 61.5 | 3L 3s, 3L 6s, 3L 9s, 3L 12s, 3L 15s, 18L 3s | |
| 3 | 6\39 | 184.6 | Terrain / mirkat (39df) | 3L 3s, 6L 3s, 6L 9s, 6L 15, 6L 21s, 6L 27s |
| 3 | 8\39 (5\39) |
246.2 (153.8) |
Triforce (39) | 3L 3s, 6L 3s, 9L 6s, 15L 9s |
| 3 | 16\39 (3\39) |
492.3 (92.3) |
Augene (39d) | 3L 3s, 3L 6s, 3L 9s, 12L 3s, 12L 15s |
| 3 | 17\39 (4\39) |
523.1 (123.0) |
Deflated (39bd) | 3L 3s, 3L 6s, 9L 3s, 9L 12s, 9L 21s |
| 13 | 16\39 (1\39) |
492.3 (30.8) |
Tridecatonic | 13L 13s |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Octave stretch or compression
39edo's approximations of harmonics 3, 5, 7 and 13 can all be improved by slightly compressing the octave, to get a tuning like 62edt.
What follows is a comparison of stretched- and compressed-octave 39edo tunings.
- Step size: 30.973 ¢, octave size: 107.9 ¢
Stretching the octave of 39edo by around 8 ¢ results in improved primes 5, 7, 11, 17, 19 and 23, but much worse primes 2 and 3. This approximates all harmonics up to 16 within 15.2 ¢. The tuning 171zpi does this. Because it shares error evenly between 39edo's fifths, it is suited for use as a dual-fifth tuning of 39edo.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +7.9 | -12.6 | -15.1 | +1.3 | -4.7 | +7.2 | -7.1 | +5.8 | +9.2 | -0.9 | +3.3 |
| Relative (%) | +25.7 | -40.7 | -48.7 | +4.1 | -15.0 | +23.3 | -23.0 | +18.6 | +29.7 | -3.0 | +10.6 | |
| Step | 39 | 61 | 77 | 90 | 100 | 109 | 116 | 123 | 129 | 134 | 139 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -11.4 | +15.2 | -11.3 | +0.8 | -11.2 | +13.7 | +13.0 | -13.8 | -5.4 | +7.0 | -8.0 | +11.2 |
| Relative (%) | -36.8 | +49.0 | -36.6 | +2.6 | -36.2 | +44.3 | +42.1 | -44.6 | -17.3 | +22.6 | -25.8 | +36.3 | |
| Step | 143 | 148 | 151 | 155 | 158 | 162 | 165 | 167 | 170 | 173 | 175 | 178 | |
- 39edo
- Step size: 30.769 ¢, octave size: 1200.00 ¢
Pure-octaves 39edo approximates all harmonics up to 16 within 15.0 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +5.7 | +0.0 | +13.7 | +5.7 | -15.0 | +0.0 | +11.5 | +13.7 | +2.5 | +5.7 |
| Relative (%) | +0.0 | +18.6 | +0.0 | +44.5 | +18.6 | -48.7 | +0.0 | +37.3 | +44.5 | +8.2 | +18.6 | |
| Steps (reduced) |
39 (0) |
62 (23) |
78 (0) |
91 (13) |
101 (23) |
109 (31) |
117 (0) |
124 (7) |
130 (13) |
135 (18) |
140 (23) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -9.8 | -15.0 | -11.3 | +0.0 | -12.6 | +11.5 | +10.2 | +13.7 | -9.2 | +2.5 | -12.9 | +5.7 |
| Relative (%) | -31.7 | -48.7 | -36.9 | +0.0 | -41.1 | +37.3 | +33.1 | +44.5 | -30.0 | +8.2 | -41.9 | +18.6 | |
| Steps (reduced) |
144 (27) |
148 (31) |
152 (35) |
156 (0) |
159 (3) |
163 (7) |
166 (10) |
169 (13) |
171 (15) |
174 (18) |
176 (20) |
179 (23) | |
- Step size: 30.757 ¢, octave size: 1199.5 ¢
Compressing the octave of 39edo by about half a cent results in improved primes 3, 5, 7 and 11, but a worse prime 13. This approximates all harmonics up to 16 within 14.4 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.5 | +5.0 | -1.0 | +12.6 | +4.5 | +14.4 | -1.4 | +10.0 | +12.1 | +0.9 | +4.0 |
| Relative (%) | -1.6 | +16.2 | -3.1 | +40.9 | +14.6 | +47.0 | -4.7 | +32.4 | +39.3 | +2.9 | +13.1 | |
| Step | 39 | 62 | 78 | 91 | 101 | 110 | 117 | 124 | 130 | 135 | 140 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -11.5 | +14.0 | -13.2 | -1.9 | -14.6 | +9.5 | +8.1 | +11.6 | -11.3 | +0.4 | -15.0 | +3.5 |
| Relative (%) | -37.5 | +45.4 | -42.9 | -6.2 | -47.4 | +30.8 | +26.5 | +37.8 | -36.8 | +1.3 | -48.9 | +11.5 | |
| Step | 144 | 149 | 152 | 156 | 159 | 163 | 166 | 169 | 171 | 174 | 176 | 179 | |
- Octave size: 1197.8 ¢
Compressing the octave of 101ed6 by around 2 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 12.8 ¢. The tuning 101ed6 does this. So does 172zpi whose octave differs by only 0.4 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.2 | +2.2 | -4.4 | +8.5 | +0.0 | +9.5 | -6.6 | +4.4 | +6.3 | -5.1 | -2.2 |
| Relative (%) | -7.2 | +7.2 | -14.4 | +27.7 | +0.0 | +31.1 | -21.6 | +14.4 | +20.5 | -16.7 | -7.2 | |
| Steps (reduced) |
39 (39) |
62 (62) |
78 (78) |
91 (91) |
101 (0) |
110 (9) |
117 (16) |
124 (23) |
130 (29) |
135 (34) |
140 (39) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +12.8 | +7.3 | +10.7 | -8.9 | +9.0 | +2.2 | +0.7 | +4.1 | +11.8 | -7.4 | +7.8 | -4.4 |
| Relative (%) | +41.6 | +23.9 | +34.9 | -28.9 | +29.4 | +7.2 | +2.4 | +13.3 | +38.3 | -24.0 | +25.5 | -14.4 | |
| Steps (reduced) |
145 (44) |
149 (48) |
153 (52) |
156 (55) |
160 (59) |
163 (62) |
166 (65) |
169 (68) |
172 (71) |
174 (73) |
177 (76) |
179 (78) | |
- Step size: 30.703 ¢, octave size: 1197.4 ¢
Compressing the octave of 39edo by around 2.5 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 11.4 ¢. Its 2.3.5.11 WE tuning and 2.3.5.11 TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.6 | +1.6 | -5.2 | +7.7 | -1.0 | +8.5 | -7.7 | +3.3 | +5.1 | -6.4 | -3.5 |
| Relative (%) | -8.4 | +5.3 | -16.8 | +24.9 | -3.1 | +27.7 | -25.2 | +10.6 | +16.5 | -20.9 | -11.5 | |
| Step | 39 | 62 | 78 | 91 | 101 | 110 | 117 | 124 | 130 | 135 | 140 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +11.4 | +5.9 | +9.3 | -10.3 | +7.5 | +0.7 | -0.8 | +2.5 | +10.1 | -9.0 | +6.2 | -6.1 |
| Relative (%) | +37.2 | +19.3 | +30.3 | -33.7 | +24.5 | +2.2 | -2.7 | +8.1 | +33.0 | -29.3 | +20.1 | -19.9 | |
| Step | 145 | 149 | 153 | 156 | 160 | 163 | 166 | 169 | 172 | 174 | 177 | 179 | |
- Step size: 30.672 ¢, octave size: 1196.2 ¢
Compressing the octave of 39edo by around 4 ¢ results in improved primes 3, 5, 7, 13, 17, 19 and 23, but worse primes 2 and 11. This approximates all harmonics up to 16 within 15.2 ¢. The tuning 173zpi does this. So does 62edt whose octave differs by only 0.2 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -3.8 | -0.3 | -7.6 | +4.8 | -4.1 | +5.1 | -11.4 | -0.6 | +1.0 | -10.6 | -7.9 |
| Relative (%) | -12.4 | -0.9 | -24.7 | +15.8 | -13.3 | +16.6 | -37.1 | -1.9 | +3.4 | -34.6 | -25.7 | |
| Step | 39 | 62 | 78 | 91 | 101 | 110 | 117 | 124 | 130 | 135 | 140 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +6.9 | +1.3 | +4.5 | -15.2 | +2.6 | -4.4 | -6.0 | -2.7 | +4.8 | -14.4 | +0.7 | -11.7 |
| Relative (%) | +22.5 | +4.2 | +14.8 | -49.5 | +8.4 | -14.3 | -19.4 | -9.0 | +15.7 | -46.9 | +2.2 | -38.0 | |
| Step | 145 | 149 | 153 | 156 | 160 | 163 | 166 | 169 | 172 | 174 | 177 | 179 | |
- Octave size: 1194.4 ¢
Compressing the octave of 39edo by around 5.5 ¢ results in improved primes 3, 5, 7, 13 and 17, but worse primes 2 and 11. This approximates all harmonics up to 16 within 14.4 ¢. The tuning 110ed7 does this. So does 145ed13 whose octave differs by only 0.1 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -5.6 | -3.2 | -11.2 | +0.6 | -8.8 | +0.0 | +13.8 | -6.3 | -5.0 | +13.8 | -14.4 |
| Relative (%) | -18.3 | -10.3 | -36.6 | +2.0 | -28.6 | +0.0 | +45.2 | -20.7 | -16.2 | +45.0 | -46.9 | |
| Steps (reduced) |
39 (39) |
62 (62) |
78 (78) |
91 (91) |
101 (101) |
110 (0) |
118 (8) |
124 (14) |
130 (20) |
136 (26) |
140 (30) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.2 | -5.6 | -2.5 | +8.2 | -4.8 | -11.9 | -13.6 | -10.6 | -3.2 | +8.2 | -7.5 | +10.7 |
| Relative (%) | +0.6 | -18.3 | -8.3 | +26.9 | -15.8 | -38.9 | -44.6 | -34.5 | -10.3 | +26.7 | -24.6 | +34.8 | |
| Steps (reduced) |
145 (35) |
149 (39) |
153 (43) |
157 (47) |
160 (50) |
163 (53) |
166 (56) |
169 (59) |
172 (62) |
175 (65) |
177 (67) |
180 (70) | |
- Octave size: 1194.1 ¢
Compressing the octave of 39edo by around 6 ¢ results in improved primes 3, 5, 7, 13 and 17, but worse primes 2 and 11. This approximates all harmonics up to 16 within 15.3 ¢. The tuning 91ed5 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -5.9 | -3.6 | -11.7 | +0.0 | -9.5 | -0.8 | +13.0 | -7.2 | -5.9 | +12.8 | +15.3 |
| Relative (%) | -19.2 | -11.7 | -38.3 | +0.0 | -30.9 | -2.5 | +42.5 | -23.4 | -19.2 | +41.9 | +50.0 | |
| Steps (reduced) |
39 (39) |
62 (62) |
78 (78) |
91 (0) |
101 (10) |
110 (19) |
118 (27) |
124 (33) |
130 (39) |
136 (45) |
141 (50) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.8 | -6.6 | -3.6 | +7.2 | -5.9 | -13.0 | -14.8 | -11.7 | -4.3 | +7.0 | -8.7 | +9.4 |
| Relative (%) | -2.6 | -21.6 | -11.7 | +23.4 | -19.4 | -42.6 | -48.3 | -38.3 | -14.2 | +22.8 | -28.5 | +30.8 | |
| Steps (reduced) |
145 (54) |
149 (58) |
153 (62) |
157 (66) |
160 (69) |
163 (72) |
166 (75) |
169 (78) |
172 (81) |
175 (84) |
177 (86) |
180 (89) | |
39edo and world music
Some might consider 39edo a candidate for a "universal tuning" in that it offers reasonable approximations of many different world music traditions; it is one of the simplest edos that can make this claim. Because of this, composers wishing to combine multiple world music traditions (for example, gamelan with maqam singing) within one unified framework might find 39edo an interesting possibility.
Western
39edo offers not one, but several different ways to realize the traditional Western diatonic scale. One way is to simply take a chain of fifths (the diatonic mos: 7 7 2 7 7 7 2). Because 39edo is a superpyth rather than a meantone system, this means that the harmonic quality of its diatonic scale will differ somewhat, since "minor" and "major" triads now approximate 6:7:9 and 14:18:21 respectively, rather than 10:12:15 and 4:5:6 as in meantone diatonic systems. Diatonic compositions translated onto this scale thus acquire a wildly different harmonic character, albeit still pleasing.
Another option is to use a modmos, such as 7 6 3 7 6 7 3; this scale enables us to continue using pental rather than septimal thirds, but it has a false (wolf) fifth. When translating diatonic compositions into this scale, it is possible to avoid the wolf fifth by introducing accidental notes when necessary. It is also possible to avoid the wolf fifth by extending the scale to either 7 3 3 3 7 3 3 7 3 (a modmos of type 3L 6s) or 4 3 6 3 4 3 6 4 3 3. There are other modmos scales that combine both pental and septimal harmonies. As such, a single Western classical or pop composition can be translated into 39edo in many different ways, acquiring a distinctly different but still harmonious character each time.
The mos and the modmos scales all have smaller-than-usual semitones, which makes them more effective for melody than their counterparts in 12edo or meantone systems.
Because 39edo and 12edo both have an overall sharp character and share the same major third, they have a relatively similar sound. Thus, 39edo (unlike, say, 22edo or 19edo, which are both "acquired tastes") does not sound all that xenharmonic to people used to 12edo. Check out Pachelbel's Canon in 39edo (using the 7 6 3 7 6 7 3 modmos), for example.
Indian
A similar situation arises with Indian music since the sruti system, like the Western system, also has multiple possible mappings in 39edo. Many of these are modified versions of the 17L 5s MOS (where the generator is a perfect fifth).
Arabic, Turkish, Iranian
While middle-eastern music is commonly approximated using 24edo, 39edo offers a potentially better alternative. 17edo and 24edo both satisfy the "Level 1" requirements for maqam tuning systems. 39edo is a Level 2 system because:
- It has two types of "neutral" seconds (154 and 185 cents)
- It has two minor seconds (92 and 123 cents), which when added together give a whole tone (215 cents)
whereas neither 17edo nor 24edo satisfy these properties.
39edo will likely be more suited to some middle-eastern scales than others. Specifically, Turkish music (in which the Rast makam has a "major-like" wide neutral third and a wide "neutral" second approaching 10/9), will likely be especially well suited to 39edo.
Blues / Jazz / African-American
The harmonic seventh ("barbershop seventh") tetrad is reasonably well approximated in 39edo, and some temperaments (augene in particular) give scales that are liberally supplied with them. John Coltrane might have loved augene (→ Wikipedia: Coltrane changes).
Tritone substitution, which is a major part of jazz and blues harmony, is more complicated in 39edo because there are two types of tritones. Therefore, the tritone substitution of one seventh chord will need to be a different type of seventh chord. However, this also opens new possibilities; if the substituted chord is of a more consonant type than the original, then the tritone substitution may function as a resolution rather than a suspension.
Blue notes, rather than being considered inflections, can be notated as accidentals instead; for example, a "blue major third" can be identified as either of the two neutral thirds. There are two possible mappings for 7/4 which are about equal in closeness. The sharp mapping is the normal one because it works better with the 5/4 and 3/2, but using the flat one instead (as an accidental) allows for another type of blue note.
Other
39edo offers approximations of pelog and mavila using the flat fifth as a generator. Pelog can also be approximated as 4 5 13 4 13.
It also offers many possible pentatonic scales, including the 2L 3s mos (which is 9 7 7 9 7). Slendro can be approximated using that scale or using something like the quasi-equal 8 8 8 8 7 or 8 8 7 8 8.
One expressive pentatonic scale is the oneirotonic subset 9 6 9 9 6.
Many Asian[clarification needed] and African [clarification needed] musical styles can thus be accommodated.
Instruments
Lumatone mapping
See Lumatone mapping for 39edo
Skip fretting
Skip fretting system 39 2 5 is a skip-fretting system for 39edo. All examples on this page are for 7-string guitar.
- Prime harmonics
1/1: string 2 open
2/1: string 5 fret 12 and string 7 fret 7
3/2: string 3 fret 9 and string 5 fret 4
5/4: string 1 fret 9 and string 3 fret 4
7/4: string 5 fret 8 and string 7 fret 3
11/8: string 2 fret 9 and string 4 fret 4
Prototypes
An illustrative image of a 39edo keyboard
39edo fretboard visualization
Music
- 39edo (2023)
- 39edo jam (2025)
- Sinner's Finale - Genshin Impact (microtonal cover in 39edo) (2025)
- Romance On Other Planets (2021)