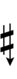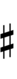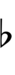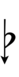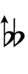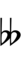43edo

← 42edo

43edo

44edo →

Prime factorization

43 (prime)

Step size

27.907¢

Fifth

25\43 (697.674¢)

Semitones (A1:m2)

3:4 (83.72¢ : 111.6¢)

Consistency limit

7

Distinct consistency limit

7

43 equal divisions of the octave (abbreviated 43edo or 43ed2), also called 43-tone equal temperament (43tet) or 43 equal temperament (43et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 43 equal parts of about 27.9 ¢ each. Each step represents a frequency ratio of 2^1/43, or the 43rd root of 2.

History

The French Baroque acoustician Joseph Sauveur, who was ironically hearing and speech impaired, based his tuning system on 43 equal tones to the octave, calling one step a méride. Sauveur favoured 43-tone equal temperament because the small intervals are well represented in it.^[1]

The composer Juhan Puhm uses 43edo in some of his fortepiano suites and prefers it to 31edo.

Theory

43edo tempers out 81/80 in the 5-limit, and as such it is strongly associated with meantone. Specifically, it is (for all practical purposes) equivalent to 1/5-comma meantone, as it tunes the major third sharp of 5/4 and perfect fifth flat of 3/2 by slightly more than four cents on both of them. It also tempers out the hypovishnuzma and the escapade comma, so that six chromatic semitones make a perfect fourth and eight minor seconds make a major sixth.

Except for 9/7, 11/9, 14/9, and 18/11, all 15-odd-limit intervals have consistent approximations in 43edo, making it an excellent tuning in the 7-, 11-, and 13-limit. In the 7-limit, it supports septimal meantone, as it tempers out 126/125, 225/224, and 3136/3125. The version of 11-limit meantone is the one tempering out 99/98, 176/175, and 441/440, sometimes called Huygens. In the 13-limit it supports meridetone, which tempers out 78/77, and grosstone, which tempers out 144/143. Meridetone has generator map ⟨0 1 4 10 18 27], for which 43 supplies the optimal patent val for, and grosstone ⟨0 1 4 10 18 -16].

43edo's patent val ⟨43 68 100 121 149 159] maps 5 to 100 steps, allowing the divison of 5 into 20 equal parts, leading to the jerome temperament, an interesting higher-limit system for which 43 supplies the optimal patent val in the 7-, 11-, 13-, 17-, 19-, and even 23-limit. It also provides the optimal patent val for the 11- and 13-limit amavil temperament, which is not meantone. Thuja is also a possibility, whose 11-limit extension makes five 11/8s stack to a major third (i.e. (11/8)⁵ → 5/1), with moses of 15 and 28.

Prime harmonics

Approximation of prime harmonics in 43edo
Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	Absolute (¢)	+0.0	-4.3	+4.4	+7.9	+6.8	-3.3	+6.7	+9.5	+13.6	+3.0	-0.8
Error	Relative (%)	+0.0	-15.3	+15.7	+28.4	+24.4	-11.9	+23.9	+33.9	+48.7	+10.7	-3.0
Steps (reduced)		43 (0)	68 (25)	100 (14)	121 (35)	149 (20)	159 (30)	176 (4)	183 (11)	195 (23)	209 (37)	213 (41)

Approximation of prime harmonics in 43edo (continued)
Harmonic		37	41	43	47	53	59	61	67	71
Error	Absolute (¢)	-0.2	-10.5	-9.2	+4.3	-8.4	+1.3	-0.6	+4.4	-12.3
Error	Relative (%)	-0.6	-37.5	-32.9	+15.3	-30.1	+4.6	-2.2	+15.8	-43.9
Steps (reduced)		224 (9)	230 (15)	233 (18)	239 (24)	246 (31)	253 (38)	255 (40)	261 (3)	264 (6)

Although not consistent, 43edo performs quite well in very high prime limits. It has unambiguous mappings for all prime harmonics up to 113 (after which the demands on its pitch resolution finally become too great), with the sole exceptions of 23, 71, 89, and 103, making a great Ringer scale. Mappings for ratios between these prime harmonics can then be derived from those for the primes themselves, allowing for a complete set of approximations to the first 16 harmonics in the harmonic series and an almost-complete approximation of the first 32 harmonics, although the limited consistency will give some unusual results. Indeed, one step of 43edo is very close to the septimal comma (64/63); similarly, two steps is close to 32/31, and four steps tunes 16/15 almost perfectly.

43edo has less than 35% relative error (less than 10 cents error) on an impressive 17 of the 19 prime harmonics in the 67-limit. The only ones it misses are 23 and 41. So it can be used as a solid full 19-limit tuning, or as a solid no-23-or-41 67-limit tuning.

It approximates harmonics 31, 37 and 61 close to exactly - within less than a cent (less than 3% relative error). It approximates 3, 13, 43, 53 and 61 slightly flat. It approximates 5, 7, 11, 17, 19, 29, 47, 59 and 67 slightly sharp. Overall this gives 43edo a slightly sharp tendency/feeling, though with the major exception of harmonic 3 (the perfect fifth).

Divisors

43edo is the 14th prime edo, following 41edo and coming before 47edo.

Intervals

The distance from C to C♯ is 3 edosteps (or keys, frets). Thus one edostep equals one third of a sharp.

#	Cents	Approximate 17-limit Ratios	Ups and Downs Notation
0	0.000	1/1	P1	perfect unison	D
1	27.907	36/35, 50/49, 64/63, 65/64, 66/65	^1, d2	up unison, dim 2nd	^D, Ebb
2	55.814	49/48, 33/32	vA1, ^d2	downaug unison, updim 2nd	vD#, ^Ebb
3	83.721	25/24, 21/20, 28/27, 22/21, 18/17	A1, vm2	aug 1sn, downminor 2nd	D#, vEb
4	111.628	16/15, 15/14, 17/16	m2	minor 2nd	Eb
5	139.535	12/11, 13/12, 14/13	^m2	upminor 2nd	^Eb
6	167.442	11/10	vM2	downmajor 2nd	vE
7	195.349	9/8, 10/9	M2	major 2nd	E
8	223.256	8/7	^M2, d3	upmajor 2nd, dim 3rd	^E, Fb
9	251.163	15/13	vA2, ^d3	downaug 2nd, updim 3rd	vE#, ^Fb
10	279.070	7/6, 13/11	A2, vm3	aug 2nd, downminor 3rd	E#, vF
11	306.977	6/5	m3	minor 3rd	F
12	334.884	39/32, 17/14	^m3	upminor 3rd	^F
13	362.791	16/13, 21/17, 11/9	vM3	downmajor 3rd	vF#
14	390.698	5/4	M3	major 3rd	F#
15	418.605	9/7, 14/11	^M3, d4	upmajor 3rd, dim 4th	^F#, Gb
16	446.512	13/10	vA3, ^d4	downaug 3rd, updim 4th	vFx, ^Gb
17	474.419	21/16	v4	down 4th	vG
18	502.326	4/3	P4	perfect 4th	G
19	530.233	15/11	^4	up 4th	^G
20	558.140	11/8, 18/13	vA4	downaug 4th	vG#
21	586.047	45/32, 7/5, 24/17	A4, vd5	aug 4th, downdim 5th	G#, ^Ab
22	613.953	64/45, 10/7, 17/12	^A4, d5	upaug 4th, dim 5th	^G#, Ab
23	641.860	16/11, 13/9	^d5	updim 5th	^Ab
24	669.767	22/15	v5	down 5th	vA
25	697.674	3/2	P5	perfect 5th	A
26	725.581	32/21	^5	up 5th	^A
27	753.488	20/13	vA5, ^d6	downaug 5th, updim 6th	vA#, ^Bbb
28	781.395	14/9, 11/7	A5, vm6	aug 5th, downminor 6th	A#, vBb
29	809.302	8/5	m6	minor 6th	Bb
30	837.209	13/8, 34/21, 18/11	^m6	upminor 6th	^Bb
31	865.116	64/39, 28/17	vM6	downmajor 6th	vB
32	893.023	5/3	M6	major 6th	B
33	920.930	12/7, 22/13	^M6, d7	upmajor 6th, dim 7th	^B, Cb
34	948.837	26/15	vA6, ^d7	downaug 6th, updim 7th	vB#, ^Cb
35	976.744	7/4	A6, vm7	aug 6th, downminor 7th	B#, vC
36	1004.651	16/9, 9/5	m7	minor 7th	C
37	1032.558	20/11	^m7	upminor 7th	^C
38	1060.465	11/6, 24/13, 13/7	vM7	downmajor 7th	vC#
39	1088.372	15/8, 28/15, 32/17	M7	major 7th	C#
40	1116.279	48/25, 40/21, 27/14, 21/11, 17/9	^M7, d8	upmajor 7th, dim 8ve	^C#, Db
41	1144.186	96/49, 64/33	vA7, ^d8	downaug 7th, updim 8ve	vCx, ^Db
42	1172.093	35/18, 49/25, 63/32, 65/33, 128/65	A7, v8	aug 7th, down 8ve	Cx, vD
43	1200.000	2/1	P8	perfect 8ve	D

Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and Downs Notation #Chords and Chord Progressions.

Approximation to JI

Selected 19-limit intervals approximated in 43edo

Interval mappings

The following tables show how 15-odd-limit intervals are represented in 43edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 43edo (direct approximation, even if inconsistent)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
15/8, 16/15	0.103	0.4
13/12, 24/13	0.962	3.4
11/7, 14/11	1.097	3.9
11/10, 20/11	2.438	8.7
13/8, 16/13	3.318	11.9
15/13, 26/15	3.422	12.3
7/5, 10/7	3.534	12.7
3/2, 4/3	4.281	15.3
5/4, 8/5	4.384	15.7
13/9, 18/13	5.243	18.8
15/11, 22/15	6.718	24.1
11/8, 16/11	6.822	24.4
13/10, 20/13	7.702	27.6
15/14, 28/15	7.815	28.0
7/4, 8/7	7.918	28.4
9/8, 16/9	8.561	30.7
5/3, 6/5	8.665	31.0
13/11, 22/13	10.140	36.3
11/6, 12/11	11.102	39.8
13/7, 14/13	11.237	40.3
9/7, 14/9	11.428	40.9
7/6, 12/7	12.199	43.7
11/9, 18/11	12.524	44.9
9/5, 10/9	12.945	46.4

15-odd-limit intervals in 43edo (patent val mapping)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
15/8, 16/15	0.103	0.4
13/12, 24/13	0.962	3.4
11/7, 14/11	1.097	3.9
11/10, 20/11	2.438	8.7
13/8, 16/13	3.318	11.9
15/13, 26/15	3.422	12.3
7/5, 10/7	3.534	12.7
3/2, 4/3	4.281	15.3
5/4, 8/5	4.384	15.7
13/9, 18/13	5.243	18.8
15/11, 22/15	6.718	24.1
11/8, 16/11	6.822	24.4
13/10, 20/13	7.702	27.6
15/14, 28/15	7.815	28.0
7/4, 8/7	7.918	28.4
9/8, 16/9	8.561	30.7
5/3, 6/5	8.665	31.0
13/11, 22/13	10.140	36.3
11/6, 12/11	11.102	39.8
13/7, 14/13	11.237	40.3
7/6, 12/7	12.199	43.7
9/5, 10/9	12.945	46.4
11/9, 18/11	15.383	55.1
9/7, 14/9	16.479	59.1

Notation

Because 43edo is a meantone system, this makes it easier to adapt traditional Western notation to it than to some other tunings. A♯ and B♭ are distinct and the distance between them is one meride. The whole tone is divided into seven merides so this means we can use "third-sharps", "two-thirds-sharps", "third-flats", and "two-thirds-flats" to reach the remaining notes between A and B; notes elsewhere on the scale can be notated similarly.

Ups and downs notation

The third-sharps and third-flats can be notated using ups and downs notation and extended Helmholtz–Ellis accidentals:

Step Offset	0	1	2	3	4	5	6	7
Sharp Symbol
Flat Symbol

The notes between A and B can then be notated as A, A , A , A♯, B♭, B , B , B. Note that A♯ is enharmonic to B , and B♭ is enharmonic to A .

The notes from B to C are B, C♭, B / C , B♯, and C. Similarily, the notes from E to F are E, F♭, E / F , E♯, and F. As with the red/blue note system described above, all notes in 43edo therefore have unambiguous names except for B / C and E / F .

Double or even triple arrows may arise if the arrows are taken to have their own layer of enharmonic spellings.

Sagittal

The following table shows sagittal notation accidentals in one apotome for 43do.

Steps	0	1	2	3
Symbol

Red-Blue Notation

For people who are not colorblind, a red-note/blue-note system (similar to that proposed for 36edo) can also be used. (Note that this is different than Kite's color notation.) Now we have the following sequence of notes, each separated by one meride: A , A , A♯ , A♯ , B♭ , B♭ , B , B . (Note that red sharps or blue flats are enharmonically equivalent to simpler notes: A♯ is enharmonic to B♭, and B♭ is actually just A♯).

The diatonic semitone is four steps, so for the region between B and C, we can use: B , C♭ , B♯ / C♭ (they are enharmonic equivalents), B♯ , and C . All of the notes in 43edo therefore have unambiguous names except for B♯ / C♭ , and E♯ / F♭ . It might also be possible to design special symbols for those two notes (resembling a cross between the letters B and C in the former case, and E and F in the latter).

If C♭ and B♯ (and F♭ / E♯ ) are instead forced to be distinct, but the requirement that all notes be equally spaced is maintained, then we end up with a completely unambiguous red-note/blue-note notation for 45edo, which is another meantone (actually, a flattone) system.

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Absolute (¢)	Relative (%)
2.3	[-68 43⟩	[⟨43 68]]	+1.35	1.35	4.84
2.3.5	81/80, 50331648/48828125	[⟨43 68 100]]	+0.27	1.88	6.75
2.3.5.7	81/80, 126/125, 17280/16807	[⟨43 68 100 121]]	−0.51	2.11	7.56
2.3.5.7.11	81/80, 99/98, 126/125, 864/847	[⟨43 68 100 121 149]]	−0.80	1.98	7.08
2.3.5.7.11.13	78/77, 81/80, 99/98, 126/125, 144/143	[⟨43 68 100 121 149 159]]	−0.52	1.91	6.85
2.3.5.7.11.13.17	78/77, 81/80, 99/98, 120/119, 126/125, 144/143	[⟨43 68 100 121 149 159 176]]	−0.52	1.81	6.49
2.3.5.7.11.13.17.19	78/77, 81/80, 99/98, 120/119, 126/125, 135/133, 144/143	[⟨], ⟨43 68 100 121 149 159 176 183]]	−0.87	1.77	6.34

Commas

This is a partial list of the 19-limit commas that 43edo tempers out with its patent val, ⟨43 68 100 121 149 159 176 183].

Prime limit	Ratio^{[note 1]}	Monzo	Cents	Color name	Name(s)
3	(42 digits)	[-68 43⟩	184.07	Tribilawa	43-comma
5	(18 digits)	[20 5 -12⟩	74.01	Saquadtrigu	Hypovishnuzma
5	(16 digits)	[24 1 -11⟩	52.50	Salegu	Magus comma
5	81/80	[-4 4 -1⟩	21.51	Gu	Syntonic comma, Didymus' comma, meantone comma
5	(20 digits)	[32 -7 -9⟩	9.49	Sasa-tritrigu	Escapade comma
5	(42 digits)	[-68 18 17⟩	2.52	Quinla-seyo	Vavoom comma
7	59049/57344	[-13 10 0 -1⟩	50.72	Laru	Harrison's comma
7	3645/3584	[-9 6 1 -1⟩	29.22	Laruyo	Schismean comma
7	(14 digits)	[5 -1 7 -7⟩	20.46	Sepruyo	Mermisma
7	126/125	[1 2 -3 1⟩	13.80	Zotrigu	Starling comma
7	(14 digits)	[21 -5 -2 -3⟩	11.12	Satriru-agugu	Bronzisma
7	(18 digits)	[-14 7 -6 6⟩	8.76	Latribizogu	Historisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Marvel comma
7	3136/3125	[6 0 -5 2⟩	6.08	Zozoquingu	Hemimean comma
7	(12 digits)	[-11 2 7 -3⟩	1.63	Latriru-asepyo	Meter
11	1350/1331	[1 3 2 0 -3⟩	24.54	Trilu-ayoyo	Large tetracot diesis
11	99/98	[-1 2 0 -2 1⟩	17.58	Loruru	Mothwellsma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	441/440	[-3 2 -1 2 -1⟩	3.93	Luzozogu	Werckisma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Triluyo	Wizardharry comma, pine comma
11	(12 digits)	[17 -5 0 -2 -1⟩	1.26	Salururu	Olympia
11	(18 digits)	[24 -6 0 1 -5⟩	0.51	Saquinlu-azo	Quartisma
13	78/77	[1 1 0 -1 -1 1⟩	22.34	Tholuru	Negustma
13	144/143	[4 2 0 0 -1 -1⟩	12.06	Thulu	Grossma
13	169/168	[-3 -1 0 -1 0 2⟩	10.27	Thothoru	Buzurgisma, dhanvantarisma
13	(12 digits)	[9 6 0 0 0 -5⟩	9.09	Quinthu	Glacier comma
13	364/363	[2 -1 0 1 -2 1⟩	4.76	Tholuluzo	Minor minthma
13	1001/1000	[-3 0 -3 1 1 1⟩	1.73	Tholozotrigu	Fairytale comma, sinbadma
13	2080/2079	[5 -3 1 -1 -1 1⟩	0.83	Tholuruyo	Ibnsinma, sinaisma
13	4096/4095	[12 -2 -1 -1 0 -1⟩	0.42	Sathurugu	Schismina
17	120/119	[3 1 1 -1 0 0 -1⟩	14.49	Suruyo	Lynchisma
17	221/220	[-2 0 -1 0 -1 1 1⟩	7.85	Sotholugu	Minor naiadma
17	256/255	[8 -1 -1 0 0 0 -1⟩	6.78	Sugu	Charisma, septendecimal kleisma
17	273/272	[5 1 -1 0 0 0 0 -1⟩	6.35	Suthozo	Tannisma
17	715/714	[-1 -1 1 -1 1 1 -1⟩	2.42	Sutholoruyo	September comma
19	96/95	[5 1 -1 0 0 0 0 -1⟩	18.13	Nugu	19th-partial chroma
19	153/152	[-3 2 0 0 0 0 1 -1⟩	11.35	Nuso	Ganassisma
19	171/170	[-1 2 -1 0 0 0 -1 1⟩	10.15	Nosugu	Malcolmisma
19	209/208	[-4 0 0 0 1 -1 0 1⟩	8.30	Nothulo	Yama comma
19	210/209	[1 1 1 1 -1 0 0 -1⟩	8.26	Nuluzoyo	Spleen comma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperaments
1	1\43	27.91	64/63	Arch
1	2\43	55.81	33/32	Escapade
1	4\43	111.63	16/15	Vavoom
1	5\43	139.53	13/12	Jerome
1	6\43	167.44	11/10	Superpine
1	7\43	195.35	28/25	Didacus
1	8\43	223.26	8/7	Kumonga
1	9\43	251.16	15/13	Hemimeantone
1	10\43	279.07	75/64	Decipentic
1	11\43	334.88	17/14	Cohemimabila
1	13\43	362.79	16/13	Submajor (43e) / interpental (43)
1	14\43	390.70	5/4	Amigo
1	16\43	446.51	13/10	Supersensi
1	18\43	502.33	4/3	Meantone
1	19\43	530.23	15/11	Amavil
1	20\43	558.14	11/8	Thuja
1	21\43	586.05	7/5	Merman

* Octave-reduced form, reduced to the first half-octave

Detemperaments

Ringer 43

The metaphorical color palette that the intervals of 43edo present can be quite appealing for various reasons such as being meantone and splitting 4/3 into 6 equal parts and 3/2 into 5 equal parts, but the accuracy leaves one wanting in many cases, which is why an excellent alternative (given the unambiguity of mappings of all primes in the 109-limit except 71 and 89) is Ringer 43, a Ringer scale with 43 notes per octave period:

55:56:57:58:59:60:61:62:63:64:65:66:67:68:69:70:72:73:74:75:76:78:79:80:82:83:84:86:87:88:90:91:92:94:96:97:98:100:102:104:106:108:109:110

Or equivalently in the form of reduced, rooted intervals:

65/64, 33/32, 67/64, 17/16, 69/64, 35/32, 9/8, 73/64, 37/32, 75/64, 19/16, 39/32, 79/64, 5/4, 41/32, 83/64, 21/16, 43/32, 87/64, 11/8, 45/32, 91/64, 23/16, 47/32, 3/2, 97/64, 49/32, 25/16, 51/64, 13/8, 53/32, 27/16, 109/64, 55/32, 7/4, 57/32, 29/16, 59/32, 15/8, 61/32, 31/16, 63/32, 2/1

Scales

Harmonic scales

43edo represents the first 16 overtones of the harmonic series well (written as a ratio of 8:9:10:11:12:13:14:15:16 in just intonation) with degrees 0, 7, 14, 20, 25, 30, 35, 39, and 43, and scale steps of 7, 7, 6, 5, 5, 5, 4, and 4.

7\43 (195.349¢) stands in for frequency ratio 9/8 (203.910¢) and 10/9 (182.404¢).
6\43 (156.522¢) stands in for 11/10 (165.004¢)
5\46 (130.435¢) stands in for 12/11 (150.637¢), 13/12 (138.573¢), and 14/13 (128.298¢).
4\43 (111.628¢) stands in for 15/14 (119.443¢) and 16/15 (111.731¢).

Harmonic	Note (starting from C)
1	C
3	G
5	E
7	A♯, B
9	D
11	E𝄪, F , F
13	B♭♭♭, A
15	B

Mos scales

Main article: List of MOS scales in 43edo

Meantone[5]: 7 7 11 7 11
Meantone[7]: 7 7 4 7 7 7 4

Other meantone scales

Major scales

Ionian Pentatonic: 14 4 7 14 4

Minor scales

Minor Harmonic: 7 4 7 7 4 10 4
Minor Harmonic Pentatonic: 7 4 14 14 4
Minor Hexatonic: 7 4 7 7 11 7
Minor Melodic: 7 4 7 7 7 7 4

Modal scales

Mixolydian Harmonic: 14 4 7 4 7 7
Mixolydian Pentatonic: 14 4 7 11 7
Phrygian Dominant: 4 10 4 7 4 7 7
Phrygian Dominant Hexatonic: 4 10 4 7 11 7
Phrygian Dominant Pentatonic: 14 4 7 4 14
Phrygian Pentatonic: 4 7 14 4 14

Blues scales

Blues Aeolian Hexatonic: 11 7 4 3 4 14
Blues Aeolian Pentatonic I: 11 7 7 4 14
Blues Aeolian Pentatonic II: 11 14 4 7 7
Blues Bright Double Harmonic: 4 10 4 7 4 7 3 4
Blues Dark Double Harmonic: 7 4 7 4 3 4 10 4
Blues Dorian Hexatonic: 11 7 7 7 4 7
Blues Dorian Pentatonic: 11 14 7 4 7
Blues Dorian Septatonic: 11 7 4 3 7 4 7
Blues Harmonic Hexatonic: 7 4 7 7 14 4
Blues Harmonic Septatonic: 11 7 4 3 4 10 4
Blues Leading: 11 7 4 3 11 3 4
Blues Minor: 11 7 4 3 11 7
Blues Minor Maj7: 11 7 4 3 14 4
Blues Pentachordal: 7 4 7 4 3 18
Hyperblue Dorian: 11 7 2 5 9 2 7
Hyperblue Harmonic: 11 7 2 5 3 12 3

Others

Akebono I: 7 4 14 7 11
Dominant Pentatonic: 7 7 11 11 7
Double Harmonic: 4 10 4 7 4 10 4
Hirajoshi: 7 4 14 4 14
Javanese Pentachordal: 4 7 11 3 18
Picardy Hexatonic: 7 7 4 7 4 14
Picardy Pentatonic: 7 7 11 4 14

Other notable scales

Fossa pentatonic scale (approximated from catnip in 60edo): 5 14 6 6 12
Magnetosphere scale (approximated from Hexany 1728): 4 10 11 11 7

Music

Modern renderings

Johann Sebastian Bach

Prelude in C minor, BWV 999 (1717–1723) – transposed into E minor, arranged for Organ and rendered by Claudi Meneghin (2024)
"Contrapunctus 4" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024)
"Contrapunctus 11" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024)