23edo
| ← 22edo | 23edo | 24edo → |
(semiconvergent)
23 equal divisions of the octave (abbreviated 23edo or 23ed2), also called 23-tone equal temperament (23tet) or 23 equal temperament (23et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 23 equal parts of about 52.2 ¢ each. Each step represents a frequency ratio of 21/23, or the 23rd root of 2.
Theory
23edo is significant in that it is the last edo that has no diatonic perfect fifths and not even 5edo or 7edo fifths. It is also the last edo that fails to approximate the 3rd, 5th, 7th, and 11th harmonics within 20 cents, which makes it well-suited for musicians seeking to explore harmonic territory that is unusual even for the average microtonalist. Oddly, despite the fact that it fails to approximate these harmonics, it approximates the intervals between them (5/3, 7/3, 11/3, 7/5, 11/5, 11/7) and combinations of them (15/8, 21/16, 33/32, 35/32, 55/32, 77/64) very well. The lowest harmonics well-approximated by 23edo are 9, 13, 15, 17, 21, 23, 31, 33 and 35.
Mapping
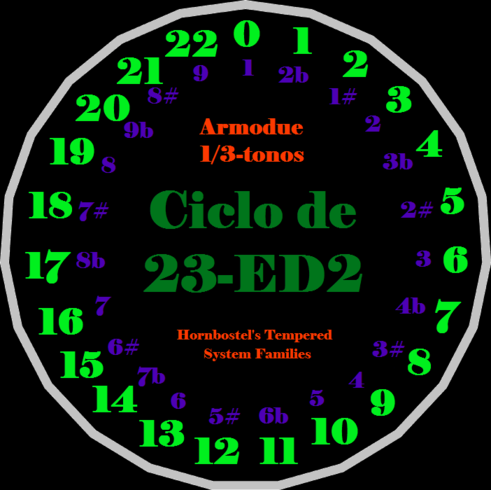
As with 9edo, 16edo, and 25edo, one way to treat 23edo is as a tuning of the mavila temperament, tempering out the "comma" of 135/128 and equating three acute 4/3's with 5/1 (related to the Armodue system). This means mapping "3/2" to 13 degrees of 23, and results in a 7-note antidiatonic scale of 3–3–4–3–3–3–4 (in steps of 23edo), which extends to a 9-note superdiatonic scale (3–3–3–1–3–3–3–3–1). One can notate 23edo using the Armodue system, but just like notating 17edo with familiar diatonic notation, flats will be lower in pitch than enharmonic sharps, because in 23edo, the "Armodue 6th" is sharper than it is in 16edo, just like the diatonic 5th in 17edo is sharper than in 12edo. In other words, 2b is lower in pitch than 1#, just like how in 17edo Eb is lower than D#.
However, one can also map 3/2 to 14 degrees of 23edo without significantly increasing the error, taking us to a 7-limit temperament where two broad 3/2's equals 7/3, meaning 28/27 is tempered out, and six 4/3's octave-reduced equals 5/4, meaning 4096/3645 is tempered out. Both of these are very large commas, so this is not at all an accurate temperament, but it is related to 13edo and 18edo and produces mos scales of 5 and 8 notes: 5–5–4–5–4 (antipentic) and 4–1–4–1–4–4–1–4 (the "quartertone" version of the Blackwood/Rapoport/Wilson 13edo "subminor" scale). Alternatively we can treat this temperament as a 2.9.21 subgroup, and instead of calling 9 degrees of 23edo a sub-"4/3", we can call it 21/16. Here three 21/16's gets us to 9/4, meaning 1029/1024 is tempered out. This allows us to treat a triad of 0–4–9 degrees of 23edo as an approximation to 16:18:21, and 0–5–9 as 1/(16:18:21); both of these triads are abundant in the 8-note mos scale.
23edo has good approximations for 5/3, 11/7, 13 and 17, among many others, allowing it to represent the 2.5/3.11/7.13.17 just intonation subgroup. If to this subgroup is added the commas of no-19's 23-limit 46edo, the larger no-19's 23-limit 2*23 subgroup 2.9.15.21.33.13.17.23 is obtained. This is the largest subgroup on which 23 has the same tuning and commas as does no-19's 23-limit 46edo, and may be regarded as a basis for analyzing the harmony of 23edo so far, as approximations to just intervals goes. If one dares to take advantage of this harmony by using 23edo as a period, you get icositritonic, a 23rd-octave temperament, so that the harmony of 23edo is adequately explained by what harmonies you can achieve using only periods and zero generators.
See Harmony of 23edo for more details.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -23.7 | -21.1 | +22.5 | +4.8 | +22.6 | -5.7 | +7.4 | -0.6 | +15.5 | -1.2 | -2.2 |
| Relative (%) | -45.4 | -40.4 | +43.1 | +9.2 | +43.3 | -11.0 | +14.2 | -1.2 | +29.8 | -2.3 | -4.2 | |
| Steps (reduced) |
36 (13) |
53 (7) |
65 (19) |
73 (4) |
80 (11) |
85 (16) |
90 (21) |
94 (2) |
98 (6) |
101 (9) |
104 (12) | |
Subsets and supersets
23edo is the 9th prime edo, following 19edo and coming before 29edo, so it does not contain any nontrivial subset edos, though it contains 23ed4. 46edo, which doubles it, considerably improves most of its approximations of lower harmonics.
Miscellany
23edo was proposed by ethnomusicologist Erich von Hornbostel as the result of continuing a circle of "blown" fifths of ~678-cent fifths that (he argued) resulted from "overblowing" a bamboo pipe.
Selected just intervals
The following tables show how 15-odd-limit intervals are represented in 23edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/7, 14/11 | 0.117 | 0.2 |
| 5/3, 6/5 | 2.598 | 5.0 |
| 9/8, 16/9 | 4.786 | 9.2 |
| 13/8, 16/13 | 5.745 | 11.0 |
| 11/6, 12/11 | 5.885 | 11.3 |
| 7/6, 12/7 | 6.001 | 11.5 |
| 15/8, 16/15 | 7.383 | 14.2 |
| 11/10, 20/11 | 8.482 | 16.3 |
| 7/5, 10/7 | 8.599 | 16.5 |
| 13/9, 18/13 | 10.531 | 20.2 |
| 15/13, 26/15 | 13.129 | 25.2 |
| 15/14, 28/15 | 15.095 | 28.9 |
| 15/11, 22/15 | 15.212 | 29.2 |
| 13/10, 20/13 | 15.351 | 29.4 |
| 9/7, 14/9 | 17.693 | 33.9 |
| 11/9, 18/11 | 17.809 | 34.1 |
| 13/12, 24/13 | 17.949 | 34.4 |
| 5/4, 8/5 | 21.096 | 40.4 |
| 7/4, 8/7 | 22.478 | 43.1 |
| 11/8, 16/11 | 22.595 | 43.3 |
| 3/2, 4/3 | 23.694 | 45.4 |
| 13/11, 22/13 | 23.834 | 45.7 |
| 13/7, 14/13 | 23.950 | 45.9 |
| 9/5, 10/9 | 25.882 | 49.6 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/7, 14/11 | 0.117 | 0.2 |
| 5/3, 6/5 | 2.598 | 5.0 |
| 13/8, 16/13 | 5.745 | 11.0 |
| 13/10, 20/13 | 15.351 | 29.4 |
| 13/12, 24/13 | 17.949 | 34.4 |
| 5/4, 8/5 | 21.096 | 40.4 |
| 7/4, 8/7 | 22.478 | 43.1 |
| 11/8, 16/11 | 22.595 | 43.3 |
| 3/2, 4/3 | 23.694 | 45.4 |
| 9/5, 10/9 | 26.292 | 50.4 |
| 13/7, 14/13 | 28.223 | 54.1 |
| 13/11, 22/13 | 28.340 | 54.3 |
| 15/13, 26/15 | 39.045 | 74.8 |
| 13/9, 18/13 | 41.643 | 79.8 |
| 7/5, 10/7 | 43.575 | 83.5 |
| 11/10, 20/11 | 43.691 | 83.7 |
| 15/8, 16/15 | 44.790 | 85.8 |
| 7/6, 12/7 | 46.173 | 88.5 |
| 11/6, 12/11 | 46.289 | 88.7 |
| 9/8, 16/9 | 47.388 | 90.8 |
| 15/14, 28/15 | 67.269 | 128.9 |
| 15/11, 22/15 | 67.386 | 129.2 |
| 9/7, 14/9 | 69.867 | 133.9 |
| 11/9, 18/11 | 69.983 | 134.1 |
Notation
Conventional notation
23edo can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways.
The first, melodic notation, defines sharp/flat, major/minor, and aug/dim in terms of the antidiatonic scale, such that sharp is higher pitched than flat, and major/aug is wider than minor/dim, as would be expected. Because it does not follow diatonic conventions, conventional interval arithmetic no longer works, e.g. M2 + M2 is not M3, and D + M2 is not E. Because antidiatonic is the sister scale to diatonic, you can solve this by swapping major and minor in interval arithmetic rules. Note that the notes that form chords are different from in diatonic: for example, a major chord, P1–M3–P5, is approximately 4:5:6 as would be expected, but is notated C–E♯–G on C.
Alternatively, one can essentially pretend the antidiatonic scale is a normal diatonic, meaning that sharp is lower in pitch than flat (since the "S" step is larger than the "L" step) and major/aug is narrower than minor/dim, known as harmonic notation. The primary purpose of doing this is to allow music notated in 12edo or another diatonic system to be directly translated on the fly, or to allow support for 23edo in tools that only allow chain-of-fifths notation, and it carries over the way interval arithmetic works from diatonic notation, at the cost of notating the sizes of intervals and the shapes of chords incorrectly: that is, a major chord, P1–M3–P5, is notated C–E–G on C, but is no longer ~4:5:6 (since the third is closer to a minor third).
For the sake of clarity, the first notation is commonly called melodic notation, and the second is called harmonic notation, but this is a bit of a misnomer as both preserve different features of the notation of harmony.
| Notation | P1–M3–P5 ~ 4:5:6 | P1–M3–P5 = C–E–G on C |
|---|---|---|
| Diatonic | No | Yes |
| Antidiatonic | Yes | No |
Sagittal notation
Best fifth notation
This notation uses the same sagittal sequence as EDOs 28 and 33.
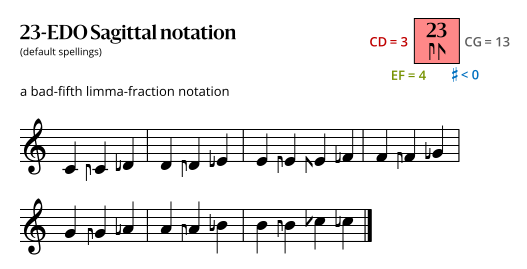
Second-best fifth notation
This notation uses the same sagittal sequence as EDOs 30, 37, and 44.

Armodue notation
Armodue notation is a nonatonic notation that uses the numbers 1-9 as note names.
| Degree | Cents | Approximate Ratios [1] |
Major wider than minor |
Major narrower than minor |
Armodue Notation |
Notes | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.000 | 1/1 | P1 | D | P1 | D | 1 | |
| 1 | 52.174 | 33/32, 34/33 | A1 | D# | d1 | Db | 2b | |
| 2 | 104.348 | 17/16, 16/15, 18/17 | d2 | Eb | A2 | E# | 1# | Less than 1 cent off 17/16 |
| 3 | 156.522 | 11/10, 12/11, 35/32 | m2 | E | M2 | E | 2 | |
| 4 | 208.696 | 9/8, 44/39 | M2 | E# | m2 | Eb | 3b | |
| 5 | 260.870 | 7/6, 15/13, 29/25 | A2, d3 | Ex, Fbb | d2, A3 | Ebb, Fx | 2# | |
| 6 | 313.043 | 6/5 | m3 | Fb | M3 | F# | 3 | Much better 6/5 than 12-edo |
| 7 | 365.217 | 16/13, 21/17, 26/21 | M3 | F | m3 | F | 4b | |
| 8 | 417.391 | 14/11, 33/26 | A3 | F# | d3 | Fb | 3# | Practically just 14/11 |
| 9 | 469.565 | 21/16, 17/13 | d4 | Gb | A4 | G# | 4 | |
| 10 | 521.739 | 23/17, 88/65, 256/189 | P4 | G | P4 | G | 5 | |
| 11 | 573.913 | 7/5, 32/23, 46/33 | A4 | G# | d4 | Gb | 6b | |
| 12 | 626.087 | 10/7, 23/16, 33/23 | d5 | Ab | A5 | A# | 5# | |
| 13 | 678.261 | 34/23, 65/44, 189/128 | P5 | A | P5 | A | 6 | Great Hornbostel generator |
| 14 | 730.435 | 32/21, 26/17 | A5 | A# | d5 | Ab | 7b | |
| 15 | 782.609 | 11/7, 52/33 | d6 | Bb | A6 | B# | 6# | Practically just 11/7 |
| 16 | 834.783 | 13/8, 34/21, 21/13 | m6 | B | M6 | B | 7 | |
| 17 | 886.957 | 5/3 | M6 | B# | m6 | Bb | 8b | Much better 5/3 than 12-edo |
| 18 | 939.130 | 12/7, 26/15, 50/29 | A6, d7 | Bx, Cbb | d6, A7 | Bbb, Cx | 7# | |
| 19 | 991.304 | 16/9, 39/22 | m7 | Cb | M7 | C# | 8 | |
| 20 | 1043.478 | 11/6, 20/11, 64/35 | M7 | C | m7 | C | 9b | |
| 21 | 1095.652 | 15/8, 17/9, 32/17 | A7 | C# | d7 | Cb | 8# | Less than 1 cent off 32/17 |
| 22 | 1147.826 | 33/17, 64/33 | d8 | Db | A8 | D# | 9 | |
| 23 | 1200.000 | 2/1 | P8 | D | P8 | D | 1 | |
- ↑ Based on treating 23-EDO as a 2.9.15.21.33.13.17 subgroup temperament; other approaches are possible.
Approximation to irrational intervals
23edo has good approximations of acoustic phi on 16\23, and pi on 38\23. Not until 72 do we find a better edo in terms of absolute error, and not until 749 do we find one in terms of relative error.
| Interval | Error (abs, ¢) |
|---|---|
| π | 0.813 |
| π/ϕ | 0.879 |
| ϕ | 1.692 |
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 22.6916 | 22.8351 | 23deff | ⟨23 36 53 64 79 84] |
| 22.8351 | 22.9754 | 23de | ⟨23 36 53 64 79 85] |
| 22.9754 | 22.9807 | 23e | ⟨23 36 53 65 79 85] |
| 22.9807 | 23.0289 | 23 | ⟨23 36 53 65 80 85] |
| 23.0289 | 23.0412 | 23b | ⟨23 37 53 65 80 85] |
| 23.0412 | 23.1054 | 23bc | ⟨23 37 54 65 80 85] |
| 23.1054 | 23.2697 | 23bcf | ⟨23 37 54 65 80 86] |
Commas
23et tempers out the following commas. This assumes the val ⟨23 36 53 65 80 85]. Also note the discussion above, where there are some commas mentioned that are not in the standard comma list (e.g., 28/27).
| Prime limit |
Ratio | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 5 | 135/128 | [-7 3 1⟩ | 92.18 | Layobi | Mavila comma, major chroma |
| 5 | 15625/15552 | [-6 -5 6⟩ | 8.11 | Tribiyo | Kleisma, semicomma majeur |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Mint comma, septimal quartertone |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's enharmonic diesis |
| 7 | 4000/3969 | [5 -4 3 -2⟩ | 13.47 | Rurutriyo | Octagar comma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutrigu | Porwell comma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
Octave stretch or compression
23edo is not often taken seriously as a tuning except by those interested in extreme xenharmony. Its fifths are significantly flat, and is neighbors 22edo and 24edo generally get more attention.
However, when using a slightly stretched octave of around 1206 cents, 23edo looks much better, and it approximates the perfect fifth (and various other intervals involving the 5th, 7th, 11th, and 13th harmonics) to within 18 cents or so. If we can tolerate errors around this size in 12edo, we can probably tolerate them in stretched-23 as well.
Stretched-23edo is one of the best tunings to use for exploring the antidiatonic scale since its fifth is more consonant and less "wolfish" than fifths in other pelogic family temperaments.
What follows is a comparison of compressed- and stretched-octave 23edo tunings.
- Step size: 51.653 ¢, octave size: 1188.0 ¢
- Approximates all harmonics <9 within 24.0 ¢
Compressing the octave of 23edo by around 12 ¢ results in improved primes 5, 11 and 13, but worse primes 2, 3 and 7. The tuning 86zpi does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -12.0 | +9.2 | -24.0 | +2.9 | -2.8 | -11.4 | +15.7 | +18.4 | -9.0 | -19.1 | -14.8 |
| Relative (%) | -23.2 | +17.8 | -46.4 | +5.7 | -5.4 | -22.0 | +30.4 | +35.6 | -17.5 | -36.9 | -28.6 | |
| Step | 23 | 37 | 46 | 54 | 60 | 65 | 70 | 74 | 77 | 80 | 83 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.6 | -23.4 | +12.2 | +3.7 | +2.1 | +6.4 | +16.1 | -21.0 | -2.2 | +20.6 | -4.7 | +24.9 |
| Relative (%) | +3.2 | -45.2 | +23.5 | +7.2 | +4.0 | +12.5 | +31.2 | -40.7 | -4.2 | +39.9 | -9.1 | +48.2 | |
| Step | 86 | 88 | 91 | 93 | 95 | 97 | 99 | 100 | 102 | 104 | 105 | 107 | |
- Step size: 51.700 ¢, octave size: 1189.1 ¢
- Approximates all harmonics <9 within 21.8 ¢
Compressing the octave of 23edo by around 11 ¢ results in improved primes 3, 5, 7 and 11, but a worse prime 2. The tuning 60ed6 does this. So does the tuning 105ed23 whose octave is identical within 0.01 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -10.9 | +10.9 | -21.8 | +5.4 | +0.0 | -8.4 | +18.9 | +21.8 | -5.5 | -15.4 | -10.9 |
| Relative (%) | -21.1 | +21.1 | -42.2 | +10.5 | +0.0 | -16.2 | +36.6 | +42.2 | -10.6 | -29.7 | -21.1 | |
| Steps (reduced) |
23 (23) |
37 (37) |
46 (46) |
54 (54) |
60 (0) |
65 (5) |
70 (10) |
74 (14) |
77 (17) |
80 (20) |
83 (23) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +5.6 | -19.3 | +16.4 | +8.0 | +6.5 | +10.9 | +20.7 | -16.4 | +2.5 | +25.4 | +0.1 | -21.8 |
| Relative (%) | +10.8 | -37.3 | +31.7 | +15.5 | +12.5 | +21.1 | +40.1 | -31.7 | +4.9 | +49.1 | +0.3 | -42.2 | |
| Steps (reduced) |
86 (26) |
88 (28) |
91 (31) |
93 (33) |
95 (35) |
97 (37) |
99 (39) |
100 (40) |
102 (42) |
104 (44) |
105 (45) |
106 (46) | |
- Step size: 52.114 ¢, octave size: 1198.6 ¢
- Approximates all harmonics <9 within 24.9 ¢
Compressing the octave of 23edo by around 1.5 ¢ results in improved primes 7 and 11, but worse primes 2, 3, 5 and 13. The tuning 85zpi does this. So does the tuning 73ed9 whose octave is identical within 0.02 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -1.4 | -25.9 | -2.8 | -24.3 | +24.9 | +18.6 | -4.1 | +0.4 | -25.6 | +17.8 | +23.5 |
| Relative (%) | -2.6 | -49.6 | -5.3 | -46.6 | +47.8 | +35.7 | -7.9 | +0.8 | -49.2 | +34.2 | +45.1 | |
| Step | 23 | 36 | 46 | 53 | 60 | 65 | 69 | 73 | 76 | 80 | 83 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -10.8 | +17.2 | +2.0 | -5.5 | -6.2 | -1.0 | +9.7 | +25.1 | -7.3 | +16.4 | -8.4 | +22.1 |
| Relative (%) | -20.8 | +33.0 | +3.8 | -10.6 | -12.0 | -1.9 | +18.5 | +48.1 | -13.9 | +31.5 | -16.2 | +42.5 | |
| Step | 85 | 88 | 90 | 92 | 94 | 96 | 98 | 100 | 101 | 103 | 104 | 106 | |
- 23edo
- Step size: 52.174 ¢, octave size: 1200.0 ¢
- Approximates all harmonics <9 within 23.7 ¢
Pure-octaves 23edo.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -23.7 | +0.0 | -21.1 | -23.7 | +22.5 | +0.0 | +4.8 | -21.1 | +22.6 | -23.7 |
| Relative (%) | +0.0 | -45.4 | +0.0 | -40.4 | -45.4 | +43.1 | +0.0 | +9.2 | -40.4 | +43.3 | -45.4 | |
| Steps (reduced) |
23 (0) |
36 (13) |
46 (0) |
53 (7) |
59 (13) |
65 (19) |
69 (0) |
73 (4) |
76 (7) |
80 (11) |
82 (13) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -5.7 | +22.5 | +7.4 | +0.0 | -0.6 | +4.8 | +15.5 | -21.1 | -1.2 | +22.6 | -2.2 | -23.7 |
| Relative (%) | -11.0 | +43.1 | +14.2 | +0.0 | -1.2 | +9.2 | +29.8 | -40.4 | -2.3 | +43.3 | -4.2 | -45.4 | |
| Steps (reduced) |
85 (16) |
88 (19) |
90 (21) |
92 (0) |
94 (2) |
96 (4) |
98 (6) |
99 (7) |
101 (9) |
103 (11) |
104 (12) |
105 (13) | |
- Step size: 52.237 ¢, octave size: 1201.5 ¢
- Approximates all harmonics <9 within 25.7 ¢
Stretching the octave of 23edo by around 1.5 ¢ results in improved primes 3, 5 and 13, but worse primes 2, 7 and 11. Its 13-limit WE tuning and 13-limit TE tuning both do this. So does the tuning 85ed13 whose octave is identical within 0.1 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.5 | -21.4 | +2.9 | -17.8 | -20.0 | -25.7 | +4.4 | +9.4 | -16.3 | -24.6 | -18.5 |
| Relative (%) | +2.8 | -41.0 | +5.6 | -34.0 | -38.2 | -49.1 | +8.3 | +18.0 | -31.2 | -47.1 | -35.5 | |
| Step | 23 | 36 | 46 | 53 | 59 | 64 | 69 | 73 | 76 | 79 | 82 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.4 | -24.2 | +13.1 | +5.8 | +5.3 | +10.8 | +21.7 | -14.9 | +5.2 | -23.1 | +4.4 | -17.1 |
| Relative (%) | -0.7 | -46.3 | +25.0 | +11.1 | +10.2 | +20.8 | +41.6 | -28.4 | +9.9 | -44.3 | +8.4 | -32.7 | |
| Step | 85 | 87 | 90 | 92 | 94 | 96 | 98 | 99 | 101 | 102 | 104 | 105 | |
- Step size: 52.447 ¢, octave size: 1206.3 ¢
- Approximates all harmonics <9 within 18.8 ¢
Stretching the octave of 23edo by around 6 ¢ results in improved primes 3, 5, 7 and 11, but worse primes 2 and 13. Its 2.3.5.13 WE tuning and 2.3.5.13 TE tuning both do this. So does the tuning 76ed10 whose octave is identical within 0.01 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +6.3 | -13.9 | +12.6 | -6.6 | -7.6 | -12.2 | +18.8 | +24.7 | -0.3 | -8.0 | -1.3 |
| Relative (%) | +12.0 | -26.4 | +24.0 | -12.6 | -14.5 | -23.3 | +35.9 | +47.1 | -0.7 | -15.3 | -2.5 | |
| Step | 23 | 36 | 46 | 53 | 59 | 64 | 69 | 73 | 76 | 79 | 82 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +17.5 | -5.9 | -20.5 | +25.1 | +25.1 | -21.4 | -10.2 | +5.9 | -26.1 | -1.7 | +26.2 | +5.0 |
| Relative (%) | +33.3 | -11.3 | -39.1 | +47.9 | +47.8 | -40.9 | -19.4 | +11.3 | -49.7 | -3.3 | +50.0 | +9.5 | |
| Step | 85 | 87 | 89 | 92 | 94 | 95 | 97 | 99 | 100 | 102 | 104 | 105 | |
- Step size: 52.575 ¢, octave size: 1209.2 ¢
- Approximates all harmonics <9 within 24.9 ¢
Stretching the octave of 23edo by around 9 ¢ results in improved primes 3, 5, 7 and 11, but worse primes 2 and 13. The tuning 59ed6 does this. So does the tuning 53ed5 whose octave is identical within 0.01 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +9.2 | -9.2 | +18.5 | +0.2 | +0.0 | -4.0 | -24.9 | -18.5 | +9.4 | +2.1 | +9.2 |
| Relative (%) | +17.6 | -17.6 | +35.1 | +0.4 | +0.0 | -7.6 | -47.3 | -35.1 | +17.9 | +4.1 | +17.6 | |
| Steps (reduced) |
23 (23) |
36 (36) |
46 (46) |
53 (53) |
59 (0) |
64 (5) |
68 (9) |
72 (13) |
76 (17) |
79 (20) |
82 (23) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -24.2 | +5.2 | -9.0 | -15.6 | -15.4 | -9.2 | +2.3 | +18.7 | -13.2 | +11.4 | -13.0 | +18.5 |
| Relative (%) | -46.0 | +10.0 | -17.2 | -29.7 | -29.4 | -17.6 | +4.4 | +35.5 | -25.2 | +21.7 | -24.7 | +35.1 | |
| Steps (reduced) |
84 (25) |
87 (28) |
89 (30) |
91 (32) |
93 (34) |
95 (36) |
97 (38) |
99 (40) |
100 (41) |
102 (43) |
103 (44) |
105 (46) | |
- Step size: 52.615 ¢, octave size: 1210.1 ¢
- Approximates all harmonics <9 within 22.2 ¢
Stretching the octave of 23edo by around 10 ¢ results in improved primes 3, 5, 7 and 11, but worse primes 2 and 13. The tuning 84zpi does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +10.1 | -7.8 | +20.3 | +2.3 | +2.3 | -1.5 | -22.2 | -15.6 | +12.4 | +5.3 | +12.5 |
| Relative (%) | +19.3 | -14.9 | +38.6 | +4.3 | +4.4 | -2.8 | -42.2 | -29.7 | +23.6 | +10.0 | +23.7 | |
| Step | 23 | 36 | 46 | 53 | 59 | 64 | 68 | 72 | 76 | 79 | 82 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -20.9 | +8.7 | -5.5 | -12.0 | -11.8 | -5.5 | +6.1 | +22.6 | -9.3 | +15.4 | -8.9 | +22.6 |
| Relative (%) | -39.7 | +16.5 | -10.5 | -22.9 | -22.4 | -10.4 | +11.7 | +42.9 | -17.6 | +29.3 | -17.0 | +43.0 | |
| Step | 84 | 87 | 89 | 91 | 93 | 95 | 97 | 99 | 100 | 102 | 103 | 105 | |
- Step size: 52.832 ¢, octave size: 1215.1 ¢
- Approximates all harmonics <9 within 22.6 ¢
Stretching the octave of 23edo by around 15 ¢ results in improved primes 3, 5, 7 and 13, but a worse prime 2. The tuning 36edt does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +15.1 | +0.0 | -22.6 | +13.8 | +15.1 | +12.4 | -7.4 | +0.0 | -23.9 | +22.4 | -22.6 |
| Relative (%) | +28.7 | +0.0 | -42.7 | +26.1 | +28.7 | +23.5 | -14.0 | +0.0 | -45.3 | +42.4 | -42.7 | |
| Steps (reduced) |
23 (23) |
36 (0) |
45 (9) |
53 (17) |
59 (23) |
64 (28) |
68 (32) |
72 (0) |
75 (3) |
79 (7) |
81 (9) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.6 | -25.3 | +13.8 | +7.7 | +8.4 | +15.1 | -25.6 | -8.8 | +12.4 | -15.3 | +13.4 | -7.4 |
| Relative (%) | -5.0 | -47.8 | +26.1 | +14.6 | +16.0 | +28.7 | -48.5 | -16.6 | +23.5 | -28.9 | +25.4 | -14.0 | |
| Steps (reduced) |
84 (12) |
86 (14) |
89 (17) |
91 (19) |
93 (21) |
95 (23) |
96 (24) |
98 (26) |
100 (28) |
101 (29) |
103 (31) |
104 (32) | |
- Step size: 52.863 ¢, octave size: 1215.9 ¢
- Approximates all harmonics <9 within 21.1 ¢
Stretching the octave of 23edo by around 16 ¢ results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. The tuning 84ed13 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +15.9 | +1.1 | -21.1 | +15.4 | +17.0 | +14.4 | -5.3 | +2.3 | -21.6 | +24.9 | -20.0 |
| Relative (%) | +30.0 | +2.1 | -40.0 | +29.2 | +32.1 | +27.3 | -10.0 | +4.3 | -40.8 | +47.1 | -37.9 | |
| Steps (reduced) |
23 (23) |
36 (36) |
45 (45) |
53 (53) |
59 (59) |
64 (64) |
68 (68) |
72 (72) |
75 (75) |
79 (79) |
81 (81) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -22.6 | +16.6 | +10.6 | +11.3 | +18.1 | -22.6 | -5.7 | +15.6 | -12.1 | +16.7 | -4.2 |
| Relative (%) | +0.0 | -42.7 | +31.4 | +20.0 | +21.5 | +34.3 | -42.8 | -10.8 | +29.4 | -22.9 | +31.5 | -7.9 | |
| Steps (reduced) |
84 (0) |
86 (2) |
89 (5) |
91 (7) |
93 (9) |
95 (11) |
96 (12) |
98 (14) |
100 (16) |
101 (17) |
103 (19) |
104 (20) | |
Scales
Important mosses include:
- Mavila 2L5s 4334333 (13\23, 1\1)
- Mavila 7L2s 133313333 (13\23, 1\1)
- Sephiroth 3L4s 2525252 (7\23, 1\1)
- Semiquartal 5L4s 332323232 (5\23, 1\1)
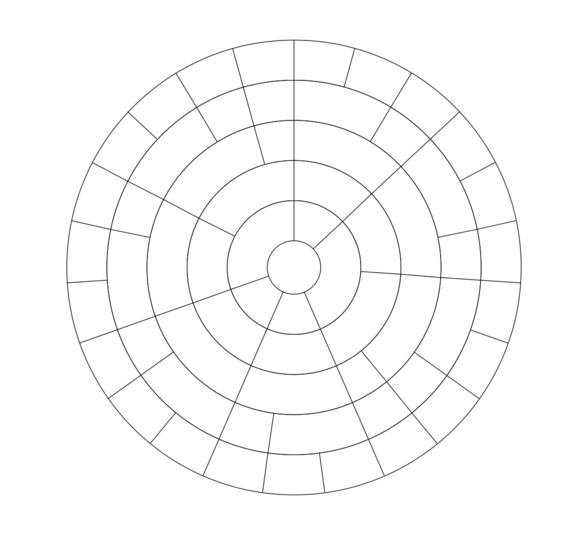
The chart below shows some of the mos modes of mavila available in 23edo, mainly Pentatonic (5-note), antidiatonic (7-note), 9- and 16-note mosses. Here the outer ring represents individual step of 23edo itself, while the rings moving inward represent 16, 9, 7 and 5 note mosses:
23-tone mos scales
| MOS scale | Name |
|---|---|
| 10 10 3 | |
| 9 9 5 | |
| 8 8 7 | |
| 7 7 7 2 | |
| 6 6 6 5 | |
| 5 4 5 5 4 | 3L 2s (oneiro-pentatonic) |
| 5 4 5 4 5 | |
| 7 1 7 7 1 | |
| 7 1 7 1 7 | |
| 5 5 5 5 3 | 4L 1s (bug pentatonic) |
| 4 4 4 4 4 3 | 5L 1s (machinoid) |
| 5 1 5 1 5 1 5 | 4L 3s (smitonic) |
| 3 3 3 5 3 3 3 | 1L 6s (antiarcheotonic) |
| 4 3 3 3 3 3 4 | |
| 3 3 4 3 3 3 4 | 2L 5s (mavila, anti-diatonic) |
| 4 3 3 3 3 4 3 | |
| 2 5 2 5 2 5 2 | 3L 4s (mosh) |
| 4 1 4 4 1 4 4 1 | 5L 3s (oneirotonic) |
| 3 3 3 3 3 3 3 2 | 7L 1s (porcupoid) |
| 3 3 3 1 3 3 3 3 1 | 7L 2s (mavila superdiatonic) |
| 3 2 3 2 3 2 3 2 3 | 5L 4s (bug semiquartal) |
| 3 2 2 3 2 2 3 2 2 2 | 3L 7s (sephiroid) |
| 4 1 1 4 1 1 4 1 1 4 1 | 4L 7s (kleistonic) |
| 3 1 3 1 3 1 3 1 3 1 3 | Palestine 11 |
| 3 1 1 3 1 3 1 1 3 1 3 1 1 | 5L 8s (ateamtonic) |
| 2 2 2 2 1 2 2 2 1 2 2 2 1 | 10L 3s (luachoid) |
| 2 2 1 2 2 1 2 2 1 2 2 1 2 1 | 9L 5s (Brittle Titanium) |
| 2 1 2 2 1 2 2 1 2 2 1 2 2 1 | Palestine 14 |
| 1 1 1 4 1 1 1 1 4 1 1 1 1 4 | 3L 11s |
| 3 1 1 1 3 1 1 1 3 1 1 1 3 1 1 | 4L 11s (mynoid) |
| 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 | 8L 7s |
| 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 1 | 7L 9s (mavila chromatic) |
| 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 | Palestine 17 |
| 2 1 1 1 2 1 1 2 1 1 1 2 1 1 2 1 1 1 | 5L 13s |
| 2 1 1 1 1 2 1 1 1 1 2 1 1 1 1 2 1 1 1 | 4L 15s |
While 35edo is the largest edo without a nondegenerate 5L 2s scale, it has both degenerate cases (the equalised 7edo and the collapsed 5edo).
23edo is the largest edo without any form of 5L 2s, including the degenerate cases.
Kosmorsky's Sephiroth modes
Kosmorsky has argued that the most significant modes of 23 edo are those of the 2 2 2 3 2 2 3 2 2 3 scale (3L 7s fair mosh); This is derived from extending the ~1/3 comma tempered 13th Harmonic, two of which add up to the 21st harmonic and three add up to the 17th harmonic almost perfectly. Interestingly, the chord 8:13:21:34 is a fragment of the fibonacci sequence.
Notated in ascending (standard) form. I have named these 10 modes according to the Sephiroth as follows:
2 2 2 3 2 2 3 2 2 3 - Mode Keter
2 2 3 2 2 3 2 2 3 2 - Chesed
2 3 2 2 3 2 2 3 2 2 - Netzach
3 2 2 3 2 2 3 2 2 2 - Malkuth
2 2 3 2 2 3 2 2 2 3 - Binah
2 3 2 2 3 2 2 2 3 2 - Tiferet
3 2 2 3 2 2 2 3 2 2 - Yesod
2 2 3 2 2 2 3 2 2 3 - Chokmah
2 3 2 2 2 3 2 2 3 2 - Gevurah
3 2 2 2 3 2 2 3 2 2 - Hod
Miscellaneous
5 5 1 2 5 5 - Antipental blues (approximated from Dwarf17marv)
7 2 4 6 4 - Arcade (approximated from 32afdo)
6 4 1 2 2 6 2 - Blackened skies (approximated from Compton in 72edo)
5 5 3 7 3 - Geode (approximated from 6afdo)
5 4 2 2 4 2 4 - Lost phantom (approximated from Mavila in 30edo)
6 4 2 1 5 1 4 - Lost spirit (approximated from Meantone in 31edo)
5 2 6 6 4 - Mechanical (approximated from 31afdo)
5 4 4 2 8 - Mushroom (approximated from 30afdo)
6 4 3 7 3 - Nightdrive (approximated from Mavila in 30edo)
6 4 1 2 6 4 - Pelagic (approximated from Mavila in 30edo)
2 3 8 2 8 - Approximation of Pelog lima
4 3 6 6 4 - Springwater (approximated from 8afdo)
2 5 2 4 6 4 - Starship (approximated from 68ifdo)
2 4 6 1 10 - Tightrope (this is the original/default tuning)
6 7 4 2 4 - Underpass (approximated from 10afdo)
2 5 6 6 4 - Volcanic (approximated from 16afdo)
Instruments
23-EDD 8-string Guitar by Ron Sword.
23-EDD Bass by Osmiorisbendi.
23-EDD Baritar by Osmiorisbendi.
23-EDD 5-string Acoustic Guitar by Tútim Dennsuul Wafiil (RIP).
Illustrative 23-EDD Keyboard
Chris Vaisvil made a do it yourself 23 edo electric guitar out of less than $50 of material. Here he is playing it.
Here is a still shot of the completed instrument.
This movie is a series of still shots Chris took during the process of making a 23 edo guitar in a stick like form. At the end the guitar is played without effects etc. and the open string tuning is sounded - which starts with a normal E and then adjusted to the 9th / 7th fret unison, like a typical 12edo guitar fashion.
Lumatone
See: Lumatone mapping for 23edo
Music
- See also: Category:23edo tracks
Further reading