Nicetone: Difference between revisions
→Tunings: Step label casing |
ArrowHead294 (talk | contribs) m Table formatting |
||
| Line 7: | Line 7: | ||
Nicetone can be tuned as a [[5-limit]] JI scale or a tempered version thereof, where L represents [[9/8]], M represents [[10/9]], and s represents [[16/15]]. | Nicetone can be tuned as a [[5-limit]] JI scale or a tempered version thereof, where L represents [[9/8]], M represents [[10/9]], and s represents [[16/15]]. | ||
{| class="wikitable" style="margin | {| class="wikitable" style="margin: auto auto auto auto;" | ||
| | |+ style="font-size: 105%;" | Comparison of Pythagorean and Ptolemaic diatonic scales in 53edo | ||
|- | |- | ||
! Name !! Structure !! Step Sizes !! Graphical Representation | ! Name !! Structure !! Step Sizes !! Graphical Representation | ||
| Line 16: | Line 16: | ||
| Pythagorean || rowspan="2" | 5L 2s || 9\53, 4\53 || ├────────┼────────┼───┼────────┼────────┼────────┼───┤ | | Pythagorean || rowspan="2" | 5L 2s || 9\53, 4\53 || ├────────┼────────┼───┼────────┼────────┼────────┼───┤ | ||
|- | |- | ||
| Meantone,<br>{{frac|5}} comma || 7\43, 4\43 || style="border: none; display: inline-block; transform: scale(calc(53 / 43), 1) translate(-2px, 0); transform-origin: left center;" | ├──────┼──────┼───┼──────┼──────┼──────┼───┤ | | Meantone, <br />{{frac|1|5}} comma || 7\43, 4\43 || style="border: none; display: inline-block; transform: scale(calc(53 / 43), 1) translate(-2px, 0); transform-origin: left center;" | ├──────┼──────┼───┼──────┼──────┼──────┼───┤ | ||
|} | |} | ||
| Line 35: | Line 35: | ||
{| class="wikitable right-2 right-3 right-4 right-5 right-6 right-7" | {| class="wikitable right-2 right-3 right-4 right-5 right-6 right-7" | ||
|+ Interval sizes in nicetone | |+ style="font-size: 105%;" | Interval sizes in nicetone | ||
|- | |- | ||
!colspan=2|Interval class | ! colspan="2" | Interval class | ||
! Sizes | ! Sizes | ||
! 5-limit JI | ! 5-limit JI | ||
! [[15edo]] <br>(L:M:s = 3:2:1) | ! [[15edo]] <br />({{nowrap|L:M:s {{=}} 3:2:1}}) | ||
! [[41edo]] <br>(L:M:s = 7:6:4) | ! [[41edo]] <br />({{nowrap|L:M:s ={{=}} 7:6:4}}) | ||
|- | |- style="background-color: #eaeaff;" | ||
!rowspan=3|Second <br>([[TAMNAMS|1-step]]) | ! rowspan="3" | Second <br />([[TAMNAMS|1-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| s | | s | ||
| 16/15, 111.73¢ | | 16/15, 111.73¢ | ||
| 1\15, 80.00¢ | | 1\15, 80.00¢ | ||
| 4\41, 117.07¢ | | 4\41, 117.07¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| M | | M | ||
| 10/9, 182.40¢ | | 10/9, 182.40¢ | ||
| 2\15, 160.00¢ | | 2\15, 160.00¢ | ||
| 6\41, 175.61¢ | | 6\41, 175.61¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| L | | L | ||
| 9/8, 203.91¢ | | 9/8, 203.91¢ | ||
| Line 62: | Line 62: | ||
| 7\41, 204.88¢ | | 7\41, 204.88¢ | ||
|- | |- | ||
!rowspan=3|Third <br>([[TAMNAMS|2-step]]) | ! rowspan="3" | Third <br />([[TAMNAMS|2-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| M + s | | M + s | ||
| 32/27, 294.13¢ | | 32/27, 294.13¢ | ||
| Line 69: | Line 69: | ||
| 10\41, 292.68¢ | | 10\41, 292.68¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| L + s | | L + s | ||
| 6/5, 315.64¢ | | 6/5, 315.64¢ | ||
| Line 75: | Line 75: | ||
| 11\41, 321.95¢ | | 11\41, 321.95¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| L + M | | L + M | ||
| 5/4, 386.31¢ | | 5/4, 386.31¢ | ||
| 5\15, 400.00¢ | | 5\15, 400.00¢ | ||
| 13\41, 380.49¢ | | 13\41, 380.49¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!rowspan=3|Fourth <br>([[TAMNAMS|3-step]]) | ! rowspan="3" | Fourth <br />([[TAMNAMS|3-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| L + M + s | | L + M + s | ||
| 4/3, 498.04¢ | | 4/3, 498.04¢ | ||
| 6\15, 480.00¢ | | 6\15, 480.00¢ | ||
| 17\41, 497.56¢ | | 17\41, 497.56¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| 2L + s | | 2L + s | ||
| 27/20, 519.55¢ | | 27/20, 519.55¢ | ||
| 7\15, 560.00¢ | | 7\15, 560.00¢ | ||
| 18\41, 526.83¢ | | 18\41, 526.83¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| 2L + M | | 2L + M | ||
| 45/32, 590.22¢ | | 45/32, 590.22¢ | ||
| Line 100: | Line 100: | ||
| 20\41, 585.37¢ | | 20\41, 585.37¢ | ||
|- | |- | ||
!rowspan=3|Fifth <br>([[TAMNAMS|4-step]]) | ! rowspan="3" | Fifth <br />([[TAMNAMS|4-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| L + M + 2s | | L + M + 2s | ||
| 64/45, 609.78¢ | | 64/45, 609.78¢ | ||
| Line 107: | Line 107: | ||
| 21\41, 614.63¢ | | 21\41, 614.63¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| L + 2M + s | | L + 2M + s | ||
| 40/27, 680.45¢ | | 40/27, 680.45¢ | ||
| Line 113: | Line 113: | ||
| 23\41, 673.17¢ | | 23\41, 673.17¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| 2L + M + s | | 2L + M + s | ||
| 3/2, 701.96¢ | | 3/2, 701.96¢ | ||
| 9\15, 720.00¢ | | 9\15, 720.00¢ | ||
| 24\41, 702.44¢ | | 24\41, 702.44¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!rowspan=3|Sixth <br>([[TAMNAMS|5-step]]) | ! rowspan="3" | Sixth <br />([[TAMNAMS|5-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| 2L + M + 2s | | 2L + M + 2s | ||
| 8/5, 813.69¢ | | 8/5, 813.69¢ | ||
| 10\15, 800.00¢ | | 10\15, 800.00¢ | ||
| 28\41, 819.51¢ | | 28\41, 819.51¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| 2L + 2M + s | | 2L + 2M + s | ||
| 5/3, 884.36¢ | | 5/3, 884.36¢ | ||
| 11\15, 880.00¢ | | 11\15, 880.00¢ | ||
| 30\41, 878.05¢ | | 30\41, 878.05¢ | ||
|- | |- style="background-color: "#eaeaff;" | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| 3L + M + s | | 3L + M + s | ||
| 27/16, 905.87¢ | | 27/16, 905.87¢ | ||
| Line 138: | Line 138: | ||
| 31\41, 907.32¢ | | 31\41, 907.32¢ | ||
|- | |- | ||
!rowspan=3|Seventh <br>([[TAMNAMS|6-step]]) | ! rowspan="3" | Seventh <br />([[TAMNAMS|6-step]]) | ||
!| | ! style="font-size: 0.75em;" | Small | ||
| 2L + 2M + 2s | | 2L + 2M + 2s | ||
| 16/9, 996.09¢ | | 16/9, 996.09¢ | ||
| Line 145: | Line 145: | ||
| 34\41, 995.12¢ | | 34\41, 995.12¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Medium | ||
| 3L + M + 2s | | 3L + M + 2s | ||
| 9/5, 1017.60¢ | | 9/5, 1017.60¢ | ||
| Line 151: | Line 151: | ||
| 35\41, 1024.39¢ | | 35\41, 1024.39¢ | ||
|- | |- | ||
!| | ! style="font-size: 0.75em;" | Large | ||
| 3L + 2M + s | | 3L + 2M + s | ||
| 15/8, 1088.27¢ | | 15/8, 1088.27¢ | ||
| Line 163: | Line 163: | ||
The modes are arranged by brightest to darkest. | The modes are arranged by brightest to darkest. | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Nicetone modes | |+ style="font-size: 105%;" | Nicetone modes | ||
!Left handed | |- | ||
!Right handed | ! Left handed !! Right handed | ||
|- | |- | ||
|LMLsMLs <br>LH Nice-Lydian | | LMLsMLs <br />LH Nice-Lydian | ||
|LMLsLMs <br>RH Nice-Lydian | | LMLsLMs <br />RH Nice-Lydian | ||
|- | |- | ||
|MLsLMLs <br>LH Nice-Ionian | | MLsLMLs <br />LH Nice-Ionian | ||
|LMsLMLs <br>RH Nice-Ionian | | LMsLMLs <br />RH Nice-Ionian | ||
|- | |- | ||
|MLsMLsL <br>LH Nice-Mixolydian | | MLsMLsL <br />LH Nice-Mixolydian | ||
|MLsLMsL <br>RH Nice-Mixolydian | | MLsLMsL <br />RH Nice-Mixolydian | ||
|- | |- | ||
|LsLMLsM <br>LH Nice-Dorian | | LsLMLsM <br />LH Nice-Dorian | ||
|MsLMLsL <br>RH Nice-Dorian | | MsLMLsL <br />RH Nice-Dorian | ||
|- | |- | ||
|LsMLsLM <br>LH Nice-Aeolian | | LsMLsLM <br />LH Nice-Aeolian | ||
|LsLMsLM <br>RH Nice-Aeolian | | LsLMsLM <br />RH Nice-Aeolian | ||
|- | |- | ||
|sLMLsML <br>LH Nice-Phrygian | | sLMLsML <br />LH Nice-Phrygian | ||
|sLMLsLM <br>RH Nice-Phrygian | | sLMLsLM <br />RH Nice-Phrygian | ||
|- | |- | ||
|sMLsLML <br>LH Nice-Locrian | | sMLsLML <br />LH Nice-Locrian | ||
|sLMsLML <br>RH Nice-Locrian | | sLMsLML <br />RH Nice-Locrian | ||
|} | |} | ||
| Line 193: | Line 193: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Tuning range of nicetone | |+ style="font-size: 105%;" | Tuning range of nicetone | ||
|- | |||
! | ! | ||
! Tuning range (in [[octave]]s) | ! Tuning range (in [[octave]]s) | ||
|- | |- | ||
! Outer generator <br>(''G''<sub>1</sub> = 2L + M + s) | ! Outer generator <br />(''G''<sub>1</sub> = 2L + M + s) | ||
| <math>\displaystyle \frac{4}{7} < G_\text{1} < \frac{2}{3}</math> | | <math>\displaystyle \frac{4}{7} < G_\text{1} < \frac{2}{3}</math> | ||
|- | |- | ||
! RH inner generator <br>(''G''<sub>2R</sub> = L + M) | ! RH inner generator <br />(''G''<sub>2R</sub> = L + M) | ||
| <math>\displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 4 G_\text{1} - 2 \text{ for } \frac{4}{7} < G_\text{1} ≤ \frac{3}{5}</math> <br><math>\displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 1 - G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3}</math> | | <math>\displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 4 G_\text{1} - 2 \text{ for } \frac{4}{7} < G_\text{1} ≤ \frac{3}{5}</math> <br><math>\displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 1 - G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3}</math> | ||
|- | |- | ||
! LH inner generator <br>(''G''<sub>2L</sub> = L + s) | ! LH inner generator <br />(''G''<sub>2L</sub> = L + s) | ||
| <math>\displaystyle 2 - 3 G_\text{1} < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{4}{7} < G_\text{1} ≤ \frac{3}{5}</math> <br><math>\displaystyle 2 G_\text{1} - 1 < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3}</math> | | <math>\displaystyle 2 - 3 G_\text{1} < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{4}{7} < G_\text{1} ≤ \frac{3}{5}</math> <br><math>\displaystyle 2 G_\text{1} - 1 < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3}</math> | ||
|- | |- | ||
! Large step <br>(L = 2''G''<sub>1</sub> - 1) | ! Large step <br />(L = 2''G''<sub>1</sub> - 1) | ||
| <math>\displaystyle \frac{1}{7} < L < \frac{1}{3}</math> | | <math>\displaystyle \frac{1}{7} < L < \frac{1}{3}</math> | ||
|- | |- | ||
! Middle step <br>(M = 1 - ''G''<sub>1</sub> - ''G''<sub>2L</sub>) | ! Middle step <br />(M = 1 - ''G''<sub>1</sub> - ''G''<sub>2L</sub>) | ||
| <math>\displaystyle \frac{1}{4} (1 - 3 L) < M < L \text{ for } \frac{1}{7} < L ≤ \frac{1}{5}</math> <br><math>\displaystyle \frac{1}{4} (1 - 3 L) < M < \frac{1}{2} (1 - 3 L) \text{ for } \frac{1}{5} ≤ L < \frac{1}{3}</math> | | <math>\displaystyle \frac{1}{4} (1 - 3 L) < M < L \text{ for } \frac{1}{7} < L ≤ \frac{1}{5}</math> <br><math>\displaystyle \frac{1}{4} (1 - 3 L) < M < \frac{1}{2} (1 - 3 L) \text{for} \frac{1}{5} ≤ L < \frac{1}{3}</math> | ||
|- | |- | ||
! Small step <br>(s = 1 - ''G''<sub>1</sub> - ''G''<sub>2R</sub>) | ! Small step <br />(s = 1 - ''G''<sub>1</sub> - ''G''<sub>2R</sub>) | ||
| <math>\displaystyle \frac{1}{2} (1 - 5 L) < s < \frac{1}{4} (1 - 3 L) \text{ for } \frac{1}{7} < L ≤ \frac{1}{5}</math> <br><math>\displaystyle 0 < s < \frac{1}{4} (1 - 3 L) \text{ for } \frac{1}{5} ≤ L < \frac{1}{3}</math> | | <math>\displaystyle \frac{1}{2} (1 - 5 L) < s < \frac{1}{4} (1 - 3 L) \text{ for } \frac{1}{7} < L ≤ \frac{1}{5}</math> <br><math>\displaystyle 0 < s < \frac{1}{4} (1 - 3 L) \text{for} \frac{1}{5} ≤ L < \frac{1}{3}</math> | ||
|} | |} | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Common Nicetone tunings | |+ style="font-size: 105%;" | Common Nicetone tunings | ||
! rowspan="2" | Tuning | |- | ||
! rowspan="2" | L:M:s | ! rowspan="2" | Tuning !! rowspan="2" | L:M:s !! colspan="3" | Size of step (¢) !! colspan="2" | Inner generator !! rowspan="2" | Outer generator <br />({{nowrap|2L + M + s}}) !! rowspan="2" | Comments | ||
! colspan="3" | Size of step (¢) | |||
! colspan="2" | Inner generator | |||
! rowspan="2" | Outer generator <br>(2L+M+s) | |||
! rowspan="2" | Comments | |||
|- | |- | ||
! L | ! L !! M !! s !! LH ({{nowrap|L + s}}) !! RH ({{nowrap|L + M}}) | ||
! M | |||
! s | |||
! LH (L+s) | |||
! RH (L+M) | |||
|- | |- | ||
| 5-limit JI || ||203.910||182.404||111.731||315.641||386.314||701.955||L=9/8, M=10/9, s=16/15 | | 5-limit JI || || 203.910 || 182.404 || 111.731 || 315.641 || 386.314 || 701.955 || {{nowrap|L {{=}} 9/8}}, {{nowrap|M {{=}} 10/9}}, {{nowrap|s {{=}} 16/15}} | ||
|- | |- | ||
|[[15edo]]||3:2:1||240.000||160.000||80.000||320.000||400.000||720.000||5-limit patent val | | [[15edo]] || 3:2:1 || 240.000 || 160.000 || 80.000 || 320.000 || 400.000 || 720.000 || 5-limit patent val | ||
|- | |- | ||
|[[18edo]]||4:2:1||266.667||133.333||66.667||333.333||400.000||733.333||5-limit patent val | | [[18edo]] || 4:2:1 || 266.667 || 133.333 || 66.667 || 333.333 || 400.000 || 733.333 || 5-limit patent val | ||
|- | |- | ||
|[[20edo]]||4:3:1||240.000||180.000||60.000||300.000||420.000||720.000|| | | [[20edo]] || 4:3:1 || 240.000 || 180.000 || 60.000 || 300.000 || 420.000 || 720.000 || | ||
|- | |- | ||
|[[21edo]]||5:2:1||285.714||114.286||57.143||342.857||400.000||742.857|| | | [[21edo]] || 5:2:1 || 285.714 || 114.286 || 57.143 || 342.857 || 400.000 || 742.857 || | ||
|- | |- | ||
|[[22edo]]||4:3:2||218.182||163.636||109.091||327.273||381.818||709.091||5-limit patent val | | [[22edo]] || 4:3:2 || 218.182 || 163.636 || 109.091 || 327.273 || 381.818 || 709.091 || 5-limit patent val | ||
|- | |- | ||
|[[23edo]]||5:3:1||260.870||156.522||52.174||313.043||417.391||730.435|| | | [[23edo]] || 5:3:1 || 260.870 || 156.522 || 52.174 || 313.043 || 417.391 || 730.435 || | ||
|- | |- | ||
|[[24edo]]||6:2:1||300.000||100.000||50.000||350.000||400.000||750.000|| | | [[24edo]] || 6:2:1 || 300.000 || 100.000 || 50.000 || 350.000 || 400.000 || 750.000 || | ||
|- | |- | ||
| rowspan="2" |[[25edo]]||5:3:2||240.000||144.000||96.000||336.000||384.000||720.000||5-limit patent val | | rowspan="2" | [[25edo]] || 5:3:2 || 240.000 || 144.000 || 96.000 || 336.000 || 384.000 || 720.000 || 5-limit patent val | ||
|- | |- | ||
|5:4:1||240.000||192.000||48.000||288.000||432.000||720.000|| | | 5:4:1 || 240.000 || 192.000 || 48.000 || 288.000 || 432.000 || 720.000 || | ||
|- | |- | ||
|[[26edo]]||6:3:1||276.923||138.462||46.154||323.077||415.385||738.462|| | | [[26edo]] || 6:3:1 || 276.923 || 138.462 || 46.154 || 323.077 || 415.385 || 738.462 || | ||
|- | |- | ||
| rowspan="2" |[[27edo]]||5:4:2||222.222||177.778||88.889||311.111||400.000||711.111||5-limit patent val | | rowspan="2" | [[27edo]] || 5:4:2 || 222.222 || 177.778 || 88.889 || 311.111 || 400.000 || 711.111 || 5-limit patent val | ||
|- | |- | ||
|7:2:1||311.111||88.889||44.444||355.556||400.000||755.556|| | | 7:2:1 || 311.111 || 88.889 || 44.444 || 355.556 || 400.000 || 755.556 || | ||
|- | |- | ||
| rowspan="2" |[[28edo]]||6:3:2||257.143||128.571||85.714||342.857||385.714||728.571|| | | rowspan="2" | [[28edo]] || 6:3:2 || 257.143 || 128.571 || 85.714 || 342.857 || 385.714 || 728.571 || | ||
|- | |- | ||
|6:4:1||257.143||171.429||42.857||300.000||428.571||728.571|| | | 6:4:1 || 257.143 || 171.429 || 42.857 || 300.000 || 428.571 || 728.571 || | ||
|- | |- | ||
| rowspan="2" |[[29edo]]||5:4:3||206.897||165.517||124.138||331.034||372.414||703.448||5-limit patent val | | rowspan="2" | [[29edo]] || 5:4:3 || 206.897 || 165.517 || 124.138 || 331.034 || 372.414 || 703.448 || 5-limit patent val | ||
|- | |- | ||
|7:3:1||289.655||124.138||41.379||331.034||413.793||744.828|| | | 7:3:1 || 289.655 || 124.138 || 41.379 || 331.034 || 413.793 || 744.828 || | ||
|- | |- | ||
| rowspan="2" |[[30edo]]||6:5:1||240.000||200.000||40.000||280.000||440.000||720.000|| | | rowspan="2" | [[30edo]] || 6:5:1 || 240.000 || 200.000 || 40.000 || 280.000 || 440.000 || 720.000 || | ||
|- | |- | ||
|8:2:1||320.000||80.000||40.000||360.000||400.000||760.000|| | | 8:2:1 || 320.000 || 80.000 || 40.000 || 360.000 || 400.000 || 760.000 || | ||
|- | |- | ||
| rowspan="2" |[[31edo]]||7:3:2||270.968||116.129||77.419||348.387||387.097||735.484|| | | rowspan="2" | [[31edo]] || 7:3:2 || 270.968 || 116.129 || 77.419 || 348.387 || 387.097 || 735.484 || | ||
|- | |- | ||
|7:4:1||270.968||154.839||38.710||309.677||425.806||735.484|| | | 7:4:1 || 270.968 || 154.839 || 38.710 || 309.677 || 425.806 || 735.484 || | ||
|- | |- | ||
| rowspan="3" |[[32edo]]||6:4:3||225.000||150.000||112.500||337.500||375.000||712.500||5-limit patent val | | rowspan="3" | [[32edo]] || 6:4:3 || 225.000 || 150.000 || 112.500 || 337.500 || 375.000 || 712.500 || 5-limit patent val | ||
|- | |- | ||
|6:5:2||225.000||187.500||75.000||300.000||412.500||712.500|| | | 6:5:2 || 225.000 || 187.500 || 75.000 || 300.000 || 412.500 || 712.500 || | ||
|- | |- | ||
|8:3:1||300.000||112.500||37.500||337.500||412.500||750.000|| | | 8:3:1 || 300.000 || 112.500 || 37.500 || 337.500 || 412.500 || 750.000 || | ||
|- | |- | ||
| rowspan="3" |[[33edo]]||7:4:2||254.545||145.455||72.727||327.273||400.000||727.273|| | | rowspan="3" | [[33edo]] || 7:4:2 || 254.545 || 145.455 || 72.727 || 327.273 || 400.000 || 727.273 || | ||
|- | |- | ||
|7:5:1||254.545||181.818||36.364||290.909||436.364||727.273|| | | 7:5:1 || 254.545 || 181.818 || 36.364 || 290.909 || 436.364 || 727.273 || | ||
|- | |- | ||
|9:2:1||327.273||72.727||36.364||363.636||400.000||763.636|| | | 9:2:1 || 327.273 || 72.727 || 36.364 || 363.636 || 400.000 || 763.636 || | ||
|- | |- | ||
| rowspan="3" |[[34edo]]||6:5:3||211.765||176.471||105.882||317.647||388.235||705.882||5-limit patent val | | rowspan="3" | [[34edo]] || 6:5:3 || 211.765 || 176.471 || 105.882 || 317.647 || 388.235 || 705.882 || 5-limit patent val | ||
|- | |- | ||
|8:3:2||282.353||105.882||70.588||352.941||388.235||741.176|| | | 8:3:2 || 282.353 || 105.882 || 70.588 || 352.941 || 388.235 || 741.176 || | ||
|- | |- | ||
|8:4:1||282.353||141.176||35.294||317.647||423.529||741.176|| | | 8:4:1 || 282.353 || 141.176 || 35.294 || 317.647 || 423.529 || 741.176 || | ||
|- | |- | ||
| rowspan="4" |[[35edo]]||7:4:3||240.000||137.143||102.857||342.857||377.143||720.000|| | | rowspan="4" | [[35edo]] || 7:4:3 || 240.000 || 137.143 || 102.857 || 342.857 || 377.143 || 720.000 || | ||
|- | |- | ||
|7:5:2||240.000||171.429||68.571||308.571||411.429||720.000|| | | 7:5:2 || 240.000 || 171.429 || 68.571 || 308.571 || 411.429 || 720.000 || | ||
|- | |- | ||
|7:6:1||240.000||205.714||34.286||274.286||445.714||720.000|| | | 7:6:1 || 240.000 || 205.714 || 34.286 || 274.286 || 445.714 || 720.000 || | ||
|- | |- | ||
|9:3:1||308.571||102.857||34.286||342.857||411.429||754.286|| | | 9:3:1 || 308.571 || 102.857 || 34.286 || 342.857 || 411.429 || 754.286 || | ||
|- | |- | ||
| rowspan="3" |[[36edo]]||6:5:4||200.000||166.667||133.333||333.333||366.667||700.000|| | | rowspan="3" | [[36edo]] || 6:5:4 || 200.000 || 166.667 || 133.333 || 333.333 || 366.667 || 700.000 || | ||
|- | |- | ||
|8:5:1||266.667||166.667||33.333||300.000||433.333||733.333|| | | 8:5:1 || 266.667 || 166.667 || 33.333 || 300.000 || 433.333 || 733.333 || | ||
|- | |- | ||
|10:2:1||333.333||66.667||33.333||366.667||400.000||766.667|| | | 10:2:1 || 333.333 || 66.667 || 33.333 || 366.667 || 400.000 || 766.667 || | ||
|- | |- | ||
| rowspan="4" |[[37edo]]||7:5:3||227.027||162.162||97.297||324.324||389.189||713.514||5-limit patent val | | rowspan="4" | [[37edo]] || 7:5:3 || 227.027 || 162.162 || 97.297 || 324.324 || 389.189 || 713.514 || 5-limit patent val | ||
|- | |- | ||
|7:6:2||227.027||194.595||64.865||291.892||421.622||713.514|| | | 7:6:2 || 227.027 || 194.595 || 64.865 || 291.892 || 421.622 || 713.514 || | ||
|- | |- | ||
|9:3:2||291.892||97.297||64.865||356.757||389.189||745.946|| | | 9:3:2 || 291.892 || 97.297 || 64.865 || 356.757 || 389.189 || 745.946 || | ||
|- | |- | ||
|9:4:1||291.892||129.730||32.432||324.324||421.622||745.946|| | | 9:4:1 || 291.892 || 129.730 || 32.432 || 324.324 || 421.622 || 745.946 || | ||
|- | |- | ||
| rowspan="4" |[[38edo]]||8:4:3||252.632||126.316||94.737||347.368||378.947||726.316|| | | rowspan="4" | [[38edo]] || 8:4:3 || 252.632 || 126.316 || 94.737 || 347.368 || 378.947 || 726.316 || | ||
|- | |- | ||
|8:5:2||252.632||157.895||63.158||315.789||410.526||726.316|| | | 8:5:2 || 252.632 || 157.895 || 63.158 || 315.789 || 410.526 || 726.316 || | ||
|- | |- | ||
|8:6:1||252.632||189.474||31.579||284.211||442.105||726.316|| | | 8:6:1 || 252.632 || 189.474 || 31.579 || 284.211 || 442.105 || 726.316 || | ||
|- | |- | ||
|10:3:1||315.789||94.737||31.579||347.368||410.526||757.895|| | | 10:3:1 || 315.789 || 94.737 || 31.579 || 347.368 || 410.526 || 757.895 || | ||
|- | |- | ||
| rowspan="5" |[[39edo]]||7:5:4||215.385||153.846||123.077||338.462||369.231||707.692|| | | rowspan="5" | [[39edo]] || 7:5:4 || 215.385 || 153.846 || 123.077 || 338.462 || 369.231 || 707.692 || | ||
|- | |- | ||
|7:6:3||215.385||184.615||92.308||307.692||400.000||707.692||5-limit patent val | | 7:6:3 || 215.385 || 184.615 || 92.308 || 307.692 || 400.000 || 707.692 || 5-limit patent val | ||
|- | |- | ||
|9:4:2||276.923||123.077||61.538||338.462||400.000||738.462|| | | 9:4:2 || 276.923 || 123.077 || 61.538 || 338.462 || 400.000 || 738.462 || | ||
|- | |- | ||
|9:5:1||276.923||153.846||30.769||307.692||430.769||738.462|| | | 9:5:1 || 276.923 || 153.846 || 30.769 || 307.692 || 430.769 || 738.462 || | ||
|- | |- | ||
|11:2:1||338.462||61.538||30.769||369.231||400.000||769.231|| | | 11:2:1 || 338.462 || 61.538 || 30.769 || 369.231 || 400.000 || 769.231 || | ||
|- | |- | ||
| rowspan="4" |[[40edo]]||8:5:3||240.000||150.000||90.000||330.000||390.000||720.000|| | | rowspan="4" | [[40edo]] || 8:5:3 || 240.000 || 150.000 || 90.000 || 330.000 || 390.000 || 720.000 || | ||
|- | |- | ||
|8:7:1||240.000||210.000||30.000||270.000||450.000||720.000|| | | 8:7:1 || 240.000 || 210.000 || 30.000 || 270.000 || 450.000 || 720.000 || | ||
|- | |- | ||
|10:3:2||300.000||90.000||60.000||360.000||390.000||750.000|| | | 10:3:2 || 300.000 || 90.000 || 60.000 || 360.000 || 390.000 || 750.000 || | ||
|- | |- | ||
|10:4:1||300.000||120.000||30.000||330.000||420.000||750.000|| | | 10:4:1 || 300.000 || 120.000 || 30.000 || 330.000 || 420.000 || 750.000 || | ||
|- | |- | ||
| rowspan="5" |[[41edo]]||7:6:4||204.878||175.610||117.073||321.951||380.488||702.439||5-limit patent val | | rowspan="5" | [[41edo]] || 7:6:4 || 204.878 || 175.610 || 117.073 || 321.951 || 380.488 || 702.439 || 5-limit patent val | ||
|- | |- | ||
|9:4:3||263.415||117.073||87.805||351.220||380.488||731.707|| | | 9:4:3 || 263.415 || 117.073 || 87.805 || 351.220 || 380.488 || 731.707 || | ||
|- | |- | ||
|9:5:2||263.415||146.341||58.537||321.951||409.756||731.707|| | | 9:5:2 || 263.415 || 146.341 || 58.537 || 321.951 || 409.756 || 731.707 || | ||
|- | |- | ||
|9:6:1||263.415||175.610||29.268||292.683||439.024||731.707|| | | 9:6:1 || 263.415 || 175.610 || 29.268 || 292.683 || 439.024 || 731.707 || | ||
|- | |- | ||
|11:3:1||321.951||87.805||29.268||351.220||409.756||760.976|| | | 11:3:1 || 321.951 || 87.805 || 29.268 || 351.220 || 409.756 || 760.976 || | ||
|- | |- | ||
| rowspan="5" |[[42edo]]||8:5:4||228.571||142.857||114.286||342.857||371.429||714.286|| | | rowspan="5" | [[42edo]] || 8:5:4 || 228.571 || 142.857 || 114.286 || 342.857 || 371.429 || 714.286 || | ||
|- | |- | ||
|8:6:3||228.571||171.429||85.714||314.286||400.000||714.286||5-limit patent val | | 8:6:3 || 228.571 || 171.429 || 85.714 || 314.286 || 400.000 || 714.286 || 5-limit patent val | ||
|- | |- | ||
|8:7:2||228.571||200.000||57.143||285.714||428.571||714.286|| | | 8:7:2 || 228.571 || 200.000 || 57.143 || 285.714 || 428.571 || 714.286 || | ||
|- | |- | ||
|10:5:1||285.714||142.857||28.571||314.286||428.571||742.857|| | | 10:5:1 || 285.714 || 142.857 || 28.571 || 314.286 || 428.571 || 742.857 || | ||
|- | |- | ||
|12:2:1||342.857||57.143||28.571||371.429||400.000||771.429|| | | 12:2:1 || 342.857 || 57.143 || 28.571 || 371.429 || 400.000 || 771.429 || | ||
|- | |- | ||
| rowspan="6" |[[43edo]]||7:6:5||195.349||167.442||139.535||334.884||362.791||697.674|| | | rowspan="6" | [[43edo]] || 7:6:5 || 195.349 || 167.442 || 139.535 || 334.884 || 362.791 || 697.674 || | ||
|- | |- | ||
|9:5:3||251.163||139.535||83.721||334.884||390.698||725.581|| | | 9:5:3 || 251.163 || 139.535 || 83.721 || 334.884 || 390.698 || 725.581 || | ||
|- | |- | ||
|9:6:2||251.163||167.442||55.814||306.977||418.605||725.581|| | | 9:6:2 || 251.163 || 167.442 || 55.814 || 306.977 || 418.605 || 725.581 || | ||
|- | |- | ||
|9:7:1||251.163||195.349||27.907||279.070||446.512||725.581|| | | 9:7:1 || 251.163 || 195.349 || 27.907 || 279.070 || 446.512 || 725.581 || | ||
|- | |- | ||
|11:3:2||306.977||83.721||55.814||362.791||390.698||753.488|| | | 11:3:2 || 306.977 || 83.721 || 55.814 || 362.791 || 390.698 || 753.488 || | ||
|- | |- | ||
|11:4:1||306.977||111.628||27.907||334.884||418.605||753.488|| | | 11:4:1 || 306.977 || 111.628 || 27.907 || 334.884 || 418.605 || 753.488 || | ||
|- | |- | ||
| rowspan="5" |[[44edo]]||8:7:3||218.182||190.909||81.818||300.000||409.091||709.091|| | | rowspan="5" | [[44edo]] || 8:7:3 || 218.182 || 190.909 || 81.818 || 300.000 || 409.091 || 709.091 || | ||
|- | |- | ||
|10:4:3||272.727||109.091||81.818||354.545||381.818||736.364|| | | 10:4:3 || 272.727 || 109.091 || 81.818 || 354.545 || 381.818 || 736.364 || | ||
|- | |- | ||
|10:5:2||272.727||136.364||54.545||327.273||409.091||736.364|| | | 10:5:2 || 272.727 || 136.364 || 54.545 || 327.273 || 409.091 || 736.364 || | ||
|- | |- | ||
|10:6:1||272.727||163.636||27.273||300.000||436.364||736.364|| | | 10:6:1 || 272.727 || 163.636 || 27.273 || 300.000 || 436.364 || 736.364 || | ||
|- | |- | ||
|12:3:1||327.273||81.818||27.273||354.545||409.091||763.636|| | | 12:3:1 || 327.273 || 81.818 || 27.273 || 354.545 || 409.091 || 763.636 || | ||
|- | |- | ||
| rowspan="6" |[[45edo]]||9:5:4||240.000||133.333||106.667||346.667||373.333||720.000|| | | rowspan="6" | [[45edo]] || 9:5:4 || 240.000 || 133.333 || 106.667 || 346.667 || 373.333 || 720.000 || | ||
|- | |- | ||
|9:7:2||240.000||186.667||53.333||293.333||426.667||720.000|| | | 9:7:2 || 240.000 || 186.667 || 53.333 || 293.333 || 426.667 || 720.000 || | ||
|- | |- | ||
|9:8:1||240.000||213.333||26.667||266.667||453.333||720.000|| | | 9:8:1 || 240.000 || 213.333 || 26.667 || 266.667 || 453.333 || 720.000 || | ||
|- | |- | ||
|11:4:2||293.333||106.667||53.333||346.667||400.000||746.667|| | | 11:4:2 || 293.333 || 106.667 || 53.333 || 346.667 || 400.000 || 746.667 || | ||
|- | |- | ||
|11:5:1||293.333||133.333||26.667||320.000||426.667||746.667|| | | 11:5:1 || 293.333 || 133.333 || 26.667 || 320.000 || 426.667 || 746.667 || | ||
|- | |- | ||
|13:2:1||346.667||53.333||26.667||373.333||400.000||773.333|| | | 13:2:1 || 346.667 || 53.333 || 26.667 || 373.333 || 400.000 || 773.333 || | ||
|- | |- | ||
| rowspan="6" |[[46edo]]||8:6:5||208.696||156.522||130.435||339.130||365.217||704.348|| | | rowspan="6" | [[46edo]] || 8:6:5 || 208.696 || 156.522 || 130.435 || 339.130 || 365.217 || 704.348 || | ||
|- | |- | ||
|8:7:4||208.696||182.609||104.348||313.043||391.304||704.348||5-limit patent val | | 8:7:4 || 208.696 || 182.609 || 104.348 || 313.043 || 391.304 || 704.348 || 5-limit patent val | ||
|- | |- | ||
|10:5:3||260.870||130.435||78.261||339.130||391.304||730.435|| | | 10:5:3 || 260.870 || 130.435 || 78.261 || 339.130 || 391.304 || 730.435 || | ||
|- | |- | ||
|10:7:1||260.870||182.609||26.087||286.957||443.478||730.435|| | | 10:7:1 || 260.870 || 182.609 || 26.087 || 286.957 || 443.478 || 730.435 || | ||
|- | |- | ||
|12:3:2||313.043||78.261||52.174||365.217||391.304||756.522|| | | 12:3:2 || 313.043 || 78.261 || 52.174 || 365.217 || 391.304 || 756.522 || | ||
|- | |- | ||
|12:4:1||313.043||104.348||26.087||339.130||417.391||756.522|| | | 12:4:1 || 313.043 || 104.348 || 26.087 || 339.130 || 417.391 || 756.522 || | ||
|- | |- | ||
| rowspan="7" |[[47edo]]||9:6:4||229.787||153.191||102.128||331.915||382.979||714.894|| | | rowspan="7" | [[47edo]] || 9:6:4 || 229.787 || 153.191 || 102.128 || 331.915 || 382.979 || 714.894 || | ||
|- | |- | ||
|9:7:3||229.787||178.723||76.596||306.383||408.511||714.894|| | | 9:7:3 || 229.787 || 178.723 || 76.596 || 306.383 || 408.511 || 714.894 || | ||
|- | |- | ||
|9:8:2||229.787||204.255||51.064||280.851||434.043||714.894|| | | 9:8:2 || 229.787 || 204.255 || 51.064 || 280.851 || 434.043 || 714.894 || | ||
|- | |- | ||
|11:4:3||280.851||102.128||76.596||357.447||382.979||740.426|| | | 11:4:3 || 280.851 || 102.128 || 76.596 || 357.447 || 382.979 || 740.426 || | ||
|- | |- | ||
|11:5:2||280.851||127.660||51.064||331.915||408.511||740.426|| | | 11:5:2 || 280.851 || 127.660 || 51.064 || 331.915 || 408.511 || 740.426 || | ||
|- | |- | ||
|11:6:1||280.851||153.191||25.532||306.383||434.043||740.426|| | | 11:6:1 || 280.851 || 153.191 || 25.532 || 306.383 || 434.043 || 740.426 || | ||
|- | |- | ||
|13:3:1||331.915||76.596||25.532||357.447||408.511||765.957|| | | 13:3:1 || 331.915 || 76.596 || 25.532 || 357.447 || 408.511 || 765.957 || | ||
|- | |- | ||
| rowspan="7" |[[48edo]]||8:7:5||200.000||175.000||125.000||325.000||375.000||700.000||5-limit patent val | | rowspan="7" | [[48edo]] || 8:7:5 || 200.000 || 175.000 || 125.000 || 325.000 || 375.000 || 700.000 || 5-limit patent val | ||
|- | |- | ||
|10:5:4||250.000||125.000||100.000||350.000||375.000||725.000|| | | 10:5:4 || 250.000 || 125.000 || 100.000 || 350.000 || 375.000 || 725.000 || | ||
|- | |- | ||
|10:6:3||250.000||150.000||75.000||325.000||400.000||725.000|| | | 10:6:3 || 250.000 || 150.000 || 75.000 || 325.000 || 400.000 || 725.000 || | ||
|- | |- | ||
|10:7:2||250.000||175.000||50.000||300.000||425.000||725.000|| | | 10:7:2 || 250.000 || 175.000 || 50.000 || 300.000 || 425.000 || 725.000 || | ||
|- | |- | ||
|10:8:1||250.000||200.000||25.000||275.000||450.000||725.000|| | | 10:8:1 || 250.000 || 200.000 || 25.000 || 275.000 || 450.000 || 725.000 || | ||
|- | |- | ||
|12:5:1||300.000||125.000||25.000||325.000||425.000||750.000|| | | 12:5:1 || 300.000 || 125.000 || 25.000 || 325.000 || 425.000 || 750.000 || | ||
|- | |- | ||
|14:2:1||350.000||50.000||25.000||375.000||400.000||775.000|| | | 14:2:1 || 350.000 || 50.000 || 25.000 || 375.000 || 400.000 || 775.000 || | ||
|- | |- | ||
| rowspan="8" |[[49edo]]||9:6:5||220.408||146.939||122.449||342.857||367.347||710.204|| | | rowspan="8" | [[49edo]] || 9:6:5 || 220.408 || 146.939 || 122.449 || 342.857 || 367.347 || 710.204 || | ||
|- | |- | ||
|9:7:4||220.408||171.429||97.959||318.367||391.837||710.204||5-limit patent val | | 9:7:4 || 220.408 || 171.429 || 97.959 || 318.367 || 391.837 || 710.204 || 5-limit patent val | ||
|- | |- | ||
|9:8:3||220.408||195.918||73.469||293.878||416.327||710.204|| | | 9:8:3 || 220.408 || 195.918 || 73.469 || 293.878 || 416.327 || 710.204 || | ||
|- | |- | ||
|11:5:3||269.388||122.449||73.469||342.857||391.837||734.694|| | | 11:5:3 || 269.388 || 122.449 || 73.469 || 342.857 || 391.837 || 734.694 || | ||
|- | |- | ||
|11:6:2||269.388||146.939||48.980||318.367||416.327||734.694|| | | 11:6:2 || 269.388 || 146.939 || 48.980 || 318.367 || 416.327 || 734.694 || | ||
|- | |- | ||
|11:7:1||269.388||171.429||24.490||293.878||440.816||734.694|| | | 11:7:1 || 269.388 || 171.429 || 24.490 || 293.878 || 440.816 || 734.694 || | ||
|- | |- | ||
|13:3:2||318.367||73.469||48.980||367.347||391.837||759.184|| | | 13:3:2 || 318.367 || 73.469 || 48.980 || 367.347 || 391.837 || 759.184 || | ||
|- | |- | ||
|13:4:1||318.367||97.959||24.490||342.857||416.327||759.184|| | | 13:4:1 || 318.367 || 97.959 || 24.490 || 342.857 || 416.327 || 759.184 || | ||
|- | |- | ||
| rowspan="7" |[[50edo]]||8:7:6||192.000||168.000||144.000||336.000||360.000||696.000|| | | rowspan="7" | [[50edo]] || 8:7:6 || 192.000 || 168.000 || 144.000 || 336.000 || 360.000 || 696.000 || | ||
|- | |- | ||
|10:7:3||240.000||168.000||72.000||312.000||408.000||720.000|| | | 10:7:3 || 240.000 || 168.000 || 72.000 || 312.000 || 408.000 || 720.000 || | ||
|- | |- | ||
|10:9:1||240.000||216.000||24.000||264.000||456.000||720.000|| | | 10:9:1 || 240.000 || 216.000 || 24.000 || 264.000 || 456.000 || 720.000 || | ||
|- | |- | ||
|12:4:3||288.000||96.000||72.000||360.000||384.000||744.000|| | | 12:4:3 || 288.000 || 96.000 || 72.000 || 360.000 || 384.000 || 744.000 || | ||
|- | |- | ||
|12:5:2||288.000||120.000||48.000||336.000||408.000||744.000|| | | 12:5:2 || 288.000 || 120.000 || 48.000 || 336.000 || 408.000 || 744.000 || | ||
|- | |- | ||
|12:6:1||288.000||144.000||24.000||312.000||432.000||744.000|| | | 12:6:1 || 288.000 || 144.000 || 24.000 || 312.000 || 432.000 || 744.000 || | ||
|- | |- | ||
|14:3:1||336.000||72.000||24.000||360.000||408.000||768.000|| | | 14:3:1 || 336.000 || 72.000 || 24.000 || 360.000 || 408.000 || 768.000 || | ||
|- | |- | ||
| rowspan="9" |[[51edo]]||9:7:5||211.765||164.706||117.647||329.412||376.471||705.882||5-limit patent val | | rowspan="9" | [[51edo]] || 9:7:5 || 211.765 || 164.706 || 117.647 || 329.412 || 376.471 || 705.882 || 5-limit patent val | ||
|- | |- | ||
|9:8:4||211.765||188.235||94.118||305.882||400.000||705.882|| | | 9:8:4 || 211.765 || 188.235 || 94.118 || 305.882 || 400.000 || 705.882 || | ||
|- | |- | ||
|11:5:4||258.824||117.647||94.118||352.941||376.471||729.412|| | | 11:5:4 || 258.824 || 117.647 || 94.118 || 352.941 || 376.471 || 729.412 || | ||
|- | |- | ||
|11:6:3||258.824||141.176||70.588||329.412||400.000||729.412|| | | 11:6:3 || 258.824 || 141.176 || 70.588 || 329.412 || 400.000 || 729.412 || | ||
|- | |- | ||
|11:7:2||258.824||164.706||47.059||305.882||423.529||729.412|| | | 11:7:2 || 258.824 || 164.706 || 47.059 || 305.882 || 423.529 || 729.412 || | ||
|- | |- | ||
|11:8:1||258.824||188.235||23.529||282.353||447.059||729.412|| | | 11:8:1 || 258.824 || 188.235 || 23.529 || 282.353 || 447.059 || 729.412 || | ||
|- | |- | ||
|13:4:2||305.882||94.118||47.059||352.941||400.000||752.941|| | | 13:4:2 || 305.882 || 94.118 || 47.059 || 352.941 || 400.000 || 752.941 || | ||
|- | |- | ||
|13:5:1||305.882||117.647||23.529||329.412||423.529||752.941|| | | 13:5:1 || 305.882 || 117.647 || 23.529 || 329.412 || 423.529 || 752.941 || | ||
|- | |- | ||
|15:2:1||352.941||47.059||23.529||376.471||400.000||776.471|| | | 15:2:1 || 352.941 || 47.059 || 23.529 || 376.471 || 400.000 || 776.471 || | ||
|- | |- | ||
| rowspan="8" |[[52edo]]||10:6:5||230.769||138.462||115.385||346.154||369.231||715.385|| | | rowspan="8" | [[52edo]] || 10:6:5 || 230.769 || 138.462 || 115.385 || 346.154 || 369.231 || 715.385 || | ||
|- | |- | ||
|10:7:4||230.769||161.538||92.308||323.077||392.308||715.385|| | | 10:7:4 || 230.769 || 161.538 || 92.308 || 323.077 || 392.308 || 715.385 || | ||
|- | |- | ||
|10:8:3||230.769||184.615||69.231||300.000||415.385||715.385|| | | 10:8:3 || 230.769 || 184.615 || 69.231 || 300.000 || 415.385 || 715.385 || | ||
|- | |- | ||
|10:9:2||230.769||207.692||46.154||276.923||438.462||715.385|| | | 10:9:2 || 230.769 || 207.692 || 46.154 || 276.923 || 438.462 || 715.385 || | ||
|- | |- | ||
|12:5:3||276.923||115.385||69.231||346.154||392.308||738.462|| | | 12:5:3 || 276.923 || 115.385 || 69.231 || 346.154 || 392.308 || 738.462 || | ||
|- | |- | ||
|12:7:1||276.923||161.538||23.077||300.000||438.462||738.462|| | | 12:7:1 || 276.923 || 161.538 || 23.077 || 300.000 || 438.462 || 738.462 || | ||
|- | |- | ||
|14:3:2||323.077||69.231||46.154||369.231||392.308||761.538|| | | 14:3:2 || 323.077 || 69.231 || 46.154 || 369.231 || 392.308 || 761.538 || | ||
|- | |- | ||
|14:4:1||323.077||92.308||23.077||346.154||415.385||761.538|| | | 14:4:1 || 323.077 || 92.308 || 23.077 || 346.154 || 415.385 || 761.538 || | ||
|- | |- | ||
| rowspan="10" |[[53edo]]||9:7:6||203.774||158.491||135.849||339.623||362.264||701.887|| | | rowspan="10" | [[53edo]] || 9:7:6 || 203.774 || 158.491 || 135.849 || 339.623 || 362.264 || 701.887 || | ||
|- | |- | ||
|9:8:5||203.774||181.132||113.208||316.981||384.906||701.887||5-limit patent val | | 9:8:5 || 203.774 || 181.132 || 113.208 || 316.981 || 384.906 || 701.887 || 5-limit patent val | ||
|- | |- | ||
|11:6:4||249.057||135.849||90.566||339.623||384.906||724.528|| | | 11:6:4 || 249.057 || 135.849 || 90.566 || 339.623 || 384.906 || 724.528 || | ||
|- | |- | ||
|11:7:3||249.057||158.491||67.925||316.981||407.547||724.528|| | | 11:7:3 || 249.057 || 158.491 || 67.925 || 316.981 || 407.547 || 724.528 || | ||
|- | |- | ||
|11:8:2||249.057||181.132||45.283||294.340||430.189||724.528|| | | 11:8:2 || 249.057 || 181.132 || 45.283 || 294.340 || 430.189 || 724.528 || | ||
|- | |- | ||
|11:9:1||249.057||203.774||22.642||271.698||452.830||724.528|| | | 11:9:1 || 249.057 || 203.774 || 22.642 || 271.698 || 452.830 || 724.528 || | ||
|- | |- | ||
|13:4:3||294.340||90.566||67.925||362.264||384.906||747.170|| | | 13:4:3 || 294.340 || 90.566 || 67.925 || 362.264 || 384.906 || 747.170 || | ||
|- | |- | ||
|13:5:2||294.340||113.208||45.283||339.623||407.547||747.170|| | | 13:5:2 || 294.340 || 113.208 || 45.283 || 339.623 || 407.547 || 747.170 || | ||
|- | |- | ||
|13:6:1||294.340||135.849||22.642||316.981||430.189||747.170|| | | 13:6:1 || 294.340 || 135.849 || 22.642 || 316.981 || 430.189 || 747.170 || | ||
|- | |- | ||
|15:3:1||339.623||67.925||22.642||362.264||407.547||769.811|| | | 15:3:1 || 339.623 || 67.925 || 22.642 || 362.264 || 407.547 || 769.811 || | ||
|- | |- | ||
| rowspan="7" |[[54edo]]||10:7:5||222.222||155.556||111.111||333.333||377.778||711.111||5-limit patent val | | rowspan="7" | [[54edo]] || 10:7:5 || 222.222 || 155.556 || 111.111 || 333.333 || 377.778 || 711.111 || 5-limit patent val | ||
|- | |- | ||
|10:9:3||222.222||200.000||66.667||288.889||422.222||711.111|| | | 10:9:3 || 222.222 || 200.000 || 66.667 || 288.889 || 422.222 || 711.111 || | ||
|- | |- | ||
|12:5:4||266.667||111.111||88.889||355.556||377.778||733.333|| | | 12:5:4 || 266.667 || 111.111 || 88.889 || 355.556 || 377.778 || 733.333 || | ||
|- | |- | ||
|12:7:2||266.667||155.556||44.444||311.111||422.222||733.333|| | | 12:7:2 || 266.667 || 155.556 || 44.444 || 311.111 || 422.222 || 733.333 || | ||
|- | |- | ||
|12:8:1||266.667||177.778||22.222||288.889||444.444||733.333|| | | 12:8:1 || 266.667 || 177.778 || 22.222 || 288.889 || 444.444 || 733.333 || | ||
|- | |- | ||
|14:5:1||311.111||111.111||22.222||333.333||422.222||755.556|| | | 14:5:1 || 311.111 || 111.111 || 22.222 || 333.333 || 422.222 || 755.556 || | ||
|- | |- | ||
|16:2:1||355.556||44.444||22.222||377.778||400.000||777.778|| | | 16:2:1 || 355.556 || 44.444 || 22.222 || 377.778 || 400.000 || 777.778 || | ||
|} | |} | ||
| Line 546: | Line 539: | ||
== See also == | == See also == | ||
* [[Blackdye]] | * [[Blackdye]] – A 10-note scale that is an extension to nicetone. | ||
* [[Zarlino]] | * [[Zarlino]] – A 5-limit JI scale with the same pattern. | ||
* [[Omnidiatonic]] | * [[Omnidiatonic]] – Sister 2L 3M 2s scale | ||
* [[Antinicetone]] | * [[Antinicetone]] – Sister 2L 2M 3s scale | ||
* [[5L 2s]] | * [[5L 2s]] – LM-equalized version of nicetone | ||
** [[5L 2s Muddles]] | ** [[5L 2s Muddles]] – Other diatonic muddles | ||
* [[3L 4s]] | * [[3L 4s]] – MS-equalized version of nicetone | ||
* [[3L 2s]] | * [[3L 2s]] – Collapsed version of nicetone | ||
[[Category:Rank-3 scales]] | [[Category:Rank-3 scales]] | ||
[[Category:7-tone scales]] | [[Category:7-tone scales]] | ||
[[Category:GO scales]] | [[Category:GO scales]] | ||
Revision as of 14:32, 9 September 2024
Nicetone (also known as the Zarlino pattern or Ptolemaic diatonic) is a 7-note maximum-variety-3 scale with the step signature 3L 2M 2s. Nicetone is a chiral scale with left-handed (LH, step pattern LMLsMLs) and right-handed (RH, step pattern LMLsLMs) variants that are rotationally non-equivalent. 15edo is the first equal division that supports nicetone.
Nicetone has the same pattern of the 5-limit Zarlino scale, though it encompasses the whole range of 3L 2M 2s. It's also a subset of the 5L 2m 3s blackdye scale.
Nicetone is intermediate between the 5L 2s diatonic scale and the 3L 4s neutral scale.
Nicetone can be tuned as a 5-limit JI scale or a tempered version thereof, where L represents 9/8, M represents 10/9, and s represents 16/15.
| Name | Structure | Step Sizes | Graphical Representation |
|---|---|---|---|
| Ptolemaic | 3L 2M 2s | 9\53, 8\53, 5\53 | ├────────┼───────┼────┼────────┼───────┼────────┼────┤ |
| Pythagorean | 5L 2s | 9\53, 4\53 | ├────────┼────────┼───┼────────┼────────┼────────┼───┤ |
| Meantone, 1⁄5 comma |
7\43, 4\43 | ├──────┼──────┼───┼──────┼──────┼──────┼───┤ |
| Name | Structure | Step Sizes | Graphical Representation |
|---|---|---|---|
| Mosh | 3L 4s | 7\33, 3\33 | ├──┼──────┼──┼──────┼──┼──┼──────┤ |
| Nicetone | 3L 2M 2s | 7\33, 4\33, 2\33 | ├───┼──────┼─┼──────┼───┼─┼──────┤ |
| Antipentic | 3L 2s | 7\33, 6\33 | ├─────┼──────┼──────┼─────┼──────┤ |
Intervals
The following is a table of nicetone intervals and their abstract sizes in terms of L, M and s. Given concrete sizes of L, M and s in EDO steps or cents, you can compute the concrete size of any interval in nicetone using the following expressions.
| Interval class | Sizes | 5-limit JI | 15edo (L:M:s = 3:2:1) |
41edo (= 7:6:4) | |
|---|---|---|---|---|---|
| Second (1-step) |
Small | s | 16/15, 111.73¢ | 1\15, 80.00¢ | 4\41, 117.07¢ |
| Medium | M | 10/9, 182.40¢ | 2\15, 160.00¢ | 6\41, 175.61¢ | |
| Large | L | 9/8, 203.91¢ | 3\15, 240.00¢ | 7\41, 204.88¢ | |
| Third (2-step) |
Small | M + s | 32/27, 294.13¢ | 3\15, 240.00¢ | 10\41, 292.68¢ |
| Medium | L + s | 6/5, 315.64¢ | 4\15, 320.00¢ | 11\41, 321.95¢ | |
| Large | L + M | 5/4, 386.31¢ | 5\15, 400.00¢ | 13\41, 380.49¢ | |
| Fourth (3-step) |
Small | L + M + s | 4/3, 498.04¢ | 6\15, 480.00¢ | 17\41, 497.56¢ |
| Medium | 2L + s | 27/20, 519.55¢ | 7\15, 560.00¢ | 18\41, 526.83¢ | |
| Large | 2L + M | 45/32, 590.22¢ | 8\15, 640.00¢ | 20\41, 585.37¢ | |
| Fifth (4-step) |
Small | L + M + 2s | 64/45, 609.78¢ | 7\15, 560.00¢ | 21\41, 614.63¢ |
| Medium | L + 2M + s | 40/27, 680.45¢ | 8\15, 640.00¢ | 23\41, 673.17¢ | |
| Large | 2L + M + s | 3/2, 701.96¢ | 9\15, 720.00¢ | 24\41, 702.44¢ | |
| Sixth (5-step) |
Small | 2L + M + 2s | 8/5, 813.69¢ | 10\15, 800.00¢ | 28\41, 819.51¢ |
| Medium | 2L + 2M + s | 5/3, 884.36¢ | 11\15, 880.00¢ | 30\41, 878.05¢ | |
| Large | 3L + M + s | 27/16, 905.87¢ | 12\15, 960.00¢ | 31\41, 907.32¢ | |
| Seventh (6-step) |
Small | 2L + 2M + 2s | 16/9, 996.09¢ | 12\15, 960.00¢ | 34\41, 995.12¢ |
| Medium | 3L + M + 2s | 9/5, 1017.60¢ | 13\15, 1040.00¢ | 35\41, 1024.39¢ | |
| Large | 3L + 2M + s | 15/8, 1088.27¢ | 14\15, 1120.00¢ | 37\41, 1082.93¢ | |
Modes
Nicetone has 14 modes total, with 7 LH and 7 RH modes. The names are based on their diatonic (5L 2s) counterparts.
The modes are arranged by brightest to darkest.
| Left handed | Right handed |
|---|---|
| LMLsMLs LH Nice-Lydian |
LMLsLMs RH Nice-Lydian |
| MLsLMLs LH Nice-Ionian |
LMsLMLs RH Nice-Ionian |
| MLsMLsL LH Nice-Mixolydian |
MLsLMsL RH Nice-Mixolydian |
| LsLMLsM LH Nice-Dorian |
MsLMLsL RH Nice-Dorian |
| LsMLsLM LH Nice-Aeolian |
LsLMsLM RH Nice-Aeolian |
| sLMLsML LH Nice-Phrygian |
sLMLsLM RH Nice-Phrygian |
| sMLsLML LH Nice-Locrian |
sLMsLML RH Nice-Locrian |
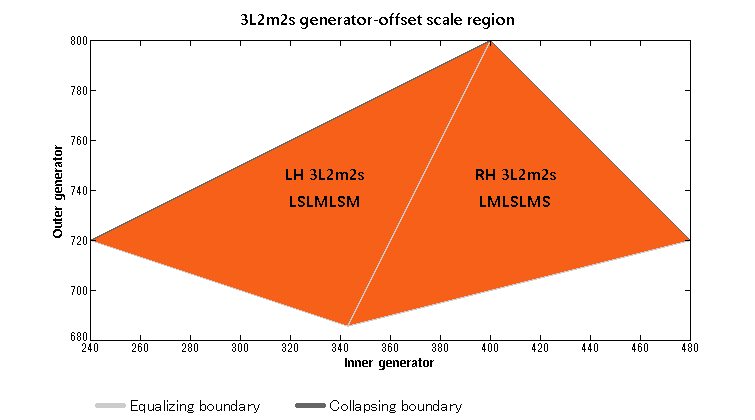
Tunings
| Tuning range (in octaves) | |
|---|---|
| Outer generator (G1 = 2L + M + s) |
[math]\displaystyle{ \displaystyle \frac{4}{7} < G_\text{1} < \frac{2}{3} }[/math] |
| RH inner generator (G2R = L + M) |
[math]\displaystyle{ \displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 4 G_\text{1} - 2 \text{ for } \frac{4}{7} < G_\text{1} ≤ \frac{3}{5} }[/math] [math]\displaystyle{ \displaystyle \frac{1}{2} G_\text{1} < G_\text{2R} < 1 - G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3} }[/math] |
| LH inner generator (G2L = L + s) |
[math]\displaystyle{ \displaystyle 2 - 3 G_\text{1} < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{4}{7} < G_\text{1} ≤ \frac{3}{5} }[/math] [math]\displaystyle{ \displaystyle 2 G_\text{1} - 1 < G_\text{2L} < \frac{1}{2} G_\text{1} \text{ for }\frac{3}{5} ≤ G_\text{1} < \frac{2}{3} }[/math] |
| Large step (L = 2G1 - 1) |
[math]\displaystyle{ \displaystyle \frac{1}{7} < L < \frac{1}{3} }[/math] |
| Middle step (M = 1 - G1 - G2L) |
[math]\displaystyle{ \displaystyle \frac{1}{4} (1 - 3 L) < M < L \text{ for } \frac{1}{7} < L ≤ \frac{1}{5} }[/math] [math]\displaystyle{ \displaystyle \frac{1}{4} (1 - 3 L) < M < \frac{1}{2} (1 - 3 L) \text{for} \frac{1}{5} ≤ L < \frac{1}{3} }[/math] |
| Small step (s = 1 - G1 - G2R) |
[math]\displaystyle{ \displaystyle \frac{1}{2} (1 - 5 L) < s < \frac{1}{4} (1 - 3 L) \text{ for } \frac{1}{7} < L ≤ \frac{1}{5} }[/math] [math]\displaystyle{ \displaystyle 0 < s < \frac{1}{4} (1 - 3 L) \text{for} \frac{1}{5} ≤ L < \frac{1}{3} }[/math] |
| Tuning | L:M:s | Size of step (¢) | Inner generator | Outer generator (2L + M + s) |
Comments | |||
|---|---|---|---|---|---|---|---|---|
| L | M | s | LH (L + s) | RH (L + M) | ||||
| 5-limit JI | 203.910 | 182.404 | 111.731 | 315.641 | 386.314 | 701.955 | L = 9/8, M = 10/9, s = 16/15 | |
| 15edo | 3:2:1 | 240.000 | 160.000 | 80.000 | 320.000 | 400.000 | 720.000 | 5-limit patent val |
| 18edo | 4:2:1 | 266.667 | 133.333 | 66.667 | 333.333 | 400.000 | 733.333 | 5-limit patent val |
| 20edo | 4:3:1 | 240.000 | 180.000 | 60.000 | 300.000 | 420.000 | 720.000 | |
| 21edo | 5:2:1 | 285.714 | 114.286 | 57.143 | 342.857 | 400.000 | 742.857 | |
| 22edo | 4:3:2 | 218.182 | 163.636 | 109.091 | 327.273 | 381.818 | 709.091 | 5-limit patent val |
| 23edo | 5:3:1 | 260.870 | 156.522 | 52.174 | 313.043 | 417.391 | 730.435 | |
| 24edo | 6:2:1 | 300.000 | 100.000 | 50.000 | 350.000 | 400.000 | 750.000 | |
| 25edo | 5:3:2 | 240.000 | 144.000 | 96.000 | 336.000 | 384.000 | 720.000 | 5-limit patent val |
| 5:4:1 | 240.000 | 192.000 | 48.000 | 288.000 | 432.000 | 720.000 | ||
| 26edo | 6:3:1 | 276.923 | 138.462 | 46.154 | 323.077 | 415.385 | 738.462 | |
| 27edo | 5:4:2 | 222.222 | 177.778 | 88.889 | 311.111 | 400.000 | 711.111 | 5-limit patent val |
| 7:2:1 | 311.111 | 88.889 | 44.444 | 355.556 | 400.000 | 755.556 | ||
| 28edo | 6:3:2 | 257.143 | 128.571 | 85.714 | 342.857 | 385.714 | 728.571 | |
| 6:4:1 | 257.143 | 171.429 | 42.857 | 300.000 | 428.571 | 728.571 | ||
| 29edo | 5:4:3 | 206.897 | 165.517 | 124.138 | 331.034 | 372.414 | 703.448 | 5-limit patent val |
| 7:3:1 | 289.655 | 124.138 | 41.379 | 331.034 | 413.793 | 744.828 | ||
| 30edo | 6:5:1 | 240.000 | 200.000 | 40.000 | 280.000 | 440.000 | 720.000 | |
| 8:2:1 | 320.000 | 80.000 | 40.000 | 360.000 | 400.000 | 760.000 | ||
| 31edo | 7:3:2 | 270.968 | 116.129 | 77.419 | 348.387 | 387.097 | 735.484 | |
| 7:4:1 | 270.968 | 154.839 | 38.710 | 309.677 | 425.806 | 735.484 | ||
| 32edo | 6:4:3 | 225.000 | 150.000 | 112.500 | 337.500 | 375.000 | 712.500 | 5-limit patent val |
| 6:5:2 | 225.000 | 187.500 | 75.000 | 300.000 | 412.500 | 712.500 | ||
| 8:3:1 | 300.000 | 112.500 | 37.500 | 337.500 | 412.500 | 750.000 | ||
| 33edo | 7:4:2 | 254.545 | 145.455 | 72.727 | 327.273 | 400.000 | 727.273 | |
| 7:5:1 | 254.545 | 181.818 | 36.364 | 290.909 | 436.364 | 727.273 | ||
| 9:2:1 | 327.273 | 72.727 | 36.364 | 363.636 | 400.000 | 763.636 | ||
| 34edo | 6:5:3 | 211.765 | 176.471 | 105.882 | 317.647 | 388.235 | 705.882 | 5-limit patent val |
| 8:3:2 | 282.353 | 105.882 | 70.588 | 352.941 | 388.235 | 741.176 | ||
| 8:4:1 | 282.353 | 141.176 | 35.294 | 317.647 | 423.529 | 741.176 | ||
| 35edo | 7:4:3 | 240.000 | 137.143 | 102.857 | 342.857 | 377.143 | 720.000 | |
| 7:5:2 | 240.000 | 171.429 | 68.571 | 308.571 | 411.429 | 720.000 | ||
| 7:6:1 | 240.000 | 205.714 | 34.286 | 274.286 | 445.714 | 720.000 | ||
| 9:3:1 | 308.571 | 102.857 | 34.286 | 342.857 | 411.429 | 754.286 | ||
| 36edo | 6:5:4 | 200.000 | 166.667 | 133.333 | 333.333 | 366.667 | 700.000 | |
| 8:5:1 | 266.667 | 166.667 | 33.333 | 300.000 | 433.333 | 733.333 | ||
| 10:2:1 | 333.333 | 66.667 | 33.333 | 366.667 | 400.000 | 766.667 | ||
| 37edo | 7:5:3 | 227.027 | 162.162 | 97.297 | 324.324 | 389.189 | 713.514 | 5-limit patent val |
| 7:6:2 | 227.027 | 194.595 | 64.865 | 291.892 | 421.622 | 713.514 | ||
| 9:3:2 | 291.892 | 97.297 | 64.865 | 356.757 | 389.189 | 745.946 | ||
| 9:4:1 | 291.892 | 129.730 | 32.432 | 324.324 | 421.622 | 745.946 | ||
| 38edo | 8:4:3 | 252.632 | 126.316 | 94.737 | 347.368 | 378.947 | 726.316 | |
| 8:5:2 | 252.632 | 157.895 | 63.158 | 315.789 | 410.526 | 726.316 | ||
| 8:6:1 | 252.632 | 189.474 | 31.579 | 284.211 | 442.105 | 726.316 | ||
| 10:3:1 | 315.789 | 94.737 | 31.579 | 347.368 | 410.526 | 757.895 | ||
| 39edo | 7:5:4 | 215.385 | 153.846 | 123.077 | 338.462 | 369.231 | 707.692 | |
| 7:6:3 | 215.385 | 184.615 | 92.308 | 307.692 | 400.000 | 707.692 | 5-limit patent val | |
| 9:4:2 | 276.923 | 123.077 | 61.538 | 338.462 | 400.000 | 738.462 | ||
| 9:5:1 | 276.923 | 153.846 | 30.769 | 307.692 | 430.769 | 738.462 | ||
| 11:2:1 | 338.462 | 61.538 | 30.769 | 369.231 | 400.000 | 769.231 | ||
| 40edo | 8:5:3 | 240.000 | 150.000 | 90.000 | 330.000 | 390.000 | 720.000 | |
| 8:7:1 | 240.000 | 210.000 | 30.000 | 270.000 | 450.000 | 720.000 | ||
| 10:3:2 | 300.000 | 90.000 | 60.000 | 360.000 | 390.000 | 750.000 | ||
| 10:4:1 | 300.000 | 120.000 | 30.000 | 330.000 | 420.000 | 750.000 | ||
| 41edo | 7:6:4 | 204.878 | 175.610 | 117.073 | 321.951 | 380.488 | 702.439 | 5-limit patent val |
| 9:4:3 | 263.415 | 117.073 | 87.805 | 351.220 | 380.488 | 731.707 | ||
| 9:5:2 | 263.415 | 146.341 | 58.537 | 321.951 | 409.756 | 731.707 | ||
| 9:6:1 | 263.415 | 175.610 | 29.268 | 292.683 | 439.024 | 731.707 | ||
| 11:3:1 | 321.951 | 87.805 | 29.268 | 351.220 | 409.756 | 760.976 | ||
| 42edo | 8:5:4 | 228.571 | 142.857 | 114.286 | 342.857 | 371.429 | 714.286 | |
| 8:6:3 | 228.571 | 171.429 | 85.714 | 314.286 | 400.000 | 714.286 | 5-limit patent val | |
| 8:7:2 | 228.571 | 200.000 | 57.143 | 285.714 | 428.571 | 714.286 | ||
| 10:5:1 | 285.714 | 142.857 | 28.571 | 314.286 | 428.571 | 742.857 | ||
| 12:2:1 | 342.857 | 57.143 | 28.571 | 371.429 | 400.000 | 771.429 | ||
| 43edo | 7:6:5 | 195.349 | 167.442 | 139.535 | 334.884 | 362.791 | 697.674 | |
| 9:5:3 | 251.163 | 139.535 | 83.721 | 334.884 | 390.698 | 725.581 | ||
| 9:6:2 | 251.163 | 167.442 | 55.814 | 306.977 | 418.605 | 725.581 | ||
| 9:7:1 | 251.163 | 195.349 | 27.907 | 279.070 | 446.512 | 725.581 | ||
| 11:3:2 | 306.977 | 83.721 | 55.814 | 362.791 | 390.698 | 753.488 | ||
| 11:4:1 | 306.977 | 111.628 | 27.907 | 334.884 | 418.605 | 753.488 | ||
| 44edo | 8:7:3 | 218.182 | 190.909 | 81.818 | 300.000 | 409.091 | 709.091 | |
| 10:4:3 | 272.727 | 109.091 | 81.818 | 354.545 | 381.818 | 736.364 | ||
| 10:5:2 | 272.727 | 136.364 | 54.545 | 327.273 | 409.091 | 736.364 | ||
| 10:6:1 | 272.727 | 163.636 | 27.273 | 300.000 | 436.364 | 736.364 | ||
| 12:3:1 | 327.273 | 81.818 | 27.273 | 354.545 | 409.091 | 763.636 | ||
| 45edo | 9:5:4 | 240.000 | 133.333 | 106.667 | 346.667 | 373.333 | 720.000 | |
| 9:7:2 | 240.000 | 186.667 | 53.333 | 293.333 | 426.667 | 720.000 | ||
| 9:8:1 | 240.000 | 213.333 | 26.667 | 266.667 | 453.333 | 720.000 | ||
| 11:4:2 | 293.333 | 106.667 | 53.333 | 346.667 | 400.000 | 746.667 | ||
| 11:5:1 | 293.333 | 133.333 | 26.667 | 320.000 | 426.667 | 746.667 | ||
| 13:2:1 | 346.667 | 53.333 | 26.667 | 373.333 | 400.000 | 773.333 | ||
| 46edo | 8:6:5 | 208.696 | 156.522 | 130.435 | 339.130 | 365.217 | 704.348 | |
| 8:7:4 | 208.696 | 182.609 | 104.348 | 313.043 | 391.304 | 704.348 | 5-limit patent val | |
| 10:5:3 | 260.870 | 130.435 | 78.261 | 339.130 | 391.304 | 730.435 | ||
| 10:7:1 | 260.870 | 182.609 | 26.087 | 286.957 | 443.478 | 730.435 | ||
| 12:3:2 | 313.043 | 78.261 | 52.174 | 365.217 | 391.304 | 756.522 | ||
| 12:4:1 | 313.043 | 104.348 | 26.087 | 339.130 | 417.391 | 756.522 | ||
| 47edo | 9:6:4 | 229.787 | 153.191 | 102.128 | 331.915 | 382.979 | 714.894 | |
| 9:7:3 | 229.787 | 178.723 | 76.596 | 306.383 | 408.511 | 714.894 | ||
| 9:8:2 | 229.787 | 204.255 | 51.064 | 280.851 | 434.043 | 714.894 | ||
| 11:4:3 | 280.851 | 102.128 | 76.596 | 357.447 | 382.979 | 740.426 | ||
| 11:5:2 | 280.851 | 127.660 | 51.064 | 331.915 | 408.511 | 740.426 | ||
| 11:6:1 | 280.851 | 153.191 | 25.532 | 306.383 | 434.043 | 740.426 | ||
| 13:3:1 | 331.915 | 76.596 | 25.532 | 357.447 | 408.511 | 765.957 | ||
| 48edo | 8:7:5 | 200.000 | 175.000 | 125.000 | 325.000 | 375.000 | 700.000 | 5-limit patent val |
| 10:5:4 | 250.000 | 125.000 | 100.000 | 350.000 | 375.000 | 725.000 | ||
| 10:6:3 | 250.000 | 150.000 | 75.000 | 325.000 | 400.000 | 725.000 | ||
| 10:7:2 | 250.000 | 175.000 | 50.000 | 300.000 | 425.000 | 725.000 | ||
| 10:8:1 | 250.000 | 200.000 | 25.000 | 275.000 | 450.000 | 725.000 | ||
| 12:5:1 | 300.000 | 125.000 | 25.000 | 325.000 | 425.000 | 750.000 | ||
| 14:2:1 | 350.000 | 50.000 | 25.000 | 375.000 | 400.000 | 775.000 | ||
| 49edo | 9:6:5 | 220.408 | 146.939 | 122.449 | 342.857 | 367.347 | 710.204 | |
| 9:7:4 | 220.408 | 171.429 | 97.959 | 318.367 | 391.837 | 710.204 | 5-limit patent val | |
| 9:8:3 | 220.408 | 195.918 | 73.469 | 293.878 | 416.327 | 710.204 | ||
| 11:5:3 | 269.388 | 122.449 | 73.469 | 342.857 | 391.837 | 734.694 | ||
| 11:6:2 | 269.388 | 146.939 | 48.980 | 318.367 | 416.327 | 734.694 | ||
| 11:7:1 | 269.388 | 171.429 | 24.490 | 293.878 | 440.816 | 734.694 | ||
| 13:3:2 | 318.367 | 73.469 | 48.980 | 367.347 | 391.837 | 759.184 | ||
| 13:4:1 | 318.367 | 97.959 | 24.490 | 342.857 | 416.327 | 759.184 | ||
| 50edo | 8:7:6 | 192.000 | 168.000 | 144.000 | 336.000 | 360.000 | 696.000 | |
| 10:7:3 | 240.000 | 168.000 | 72.000 | 312.000 | 408.000 | 720.000 | ||
| 10:9:1 | 240.000 | 216.000 | 24.000 | 264.000 | 456.000 | 720.000 | ||
| 12:4:3 | 288.000 | 96.000 | 72.000 | 360.000 | 384.000 | 744.000 | ||
| 12:5:2 | 288.000 | 120.000 | 48.000 | 336.000 | 408.000 | 744.000 | ||
| 12:6:1 | 288.000 | 144.000 | 24.000 | 312.000 | 432.000 | 744.000 | ||
| 14:3:1 | 336.000 | 72.000 | 24.000 | 360.000 | 408.000 | 768.000 | ||
| 51edo | 9:7:5 | 211.765 | 164.706 | 117.647 | 329.412 | 376.471 | 705.882 | 5-limit patent val |
| 9:8:4 | 211.765 | 188.235 | 94.118 | 305.882 | 400.000 | 705.882 | ||
| 11:5:4 | 258.824 | 117.647 | 94.118 | 352.941 | 376.471 | 729.412 | ||
| 11:6:3 | 258.824 | 141.176 | 70.588 | 329.412 | 400.000 | 729.412 | ||
| 11:7:2 | 258.824 | 164.706 | 47.059 | 305.882 | 423.529 | 729.412 | ||
| 11:8:1 | 258.824 | 188.235 | 23.529 | 282.353 | 447.059 | 729.412 | ||
| 13:4:2 | 305.882 | 94.118 | 47.059 | 352.941 | 400.000 | 752.941 | ||
| 13:5:1 | 305.882 | 117.647 | 23.529 | 329.412 | 423.529 | 752.941 | ||
| 15:2:1 | 352.941 | 47.059 | 23.529 | 376.471 | 400.000 | 776.471 | ||
| 52edo | 10:6:5 | 230.769 | 138.462 | 115.385 | 346.154 | 369.231 | 715.385 | |
| 10:7:4 | 230.769 | 161.538 | 92.308 | 323.077 | 392.308 | 715.385 | ||
| 10:8:3 | 230.769 | 184.615 | 69.231 | 300.000 | 415.385 | 715.385 | ||
| 10:9:2 | 230.769 | 207.692 | 46.154 | 276.923 | 438.462 | 715.385 | ||
| 12:5:3 | 276.923 | 115.385 | 69.231 | 346.154 | 392.308 | 738.462 | ||
| 12:7:1 | 276.923 | 161.538 | 23.077 | 300.000 | 438.462 | 738.462 | ||
| 14:3:2 | 323.077 | 69.231 | 46.154 | 369.231 | 392.308 | 761.538 | ||
| 14:4:1 | 323.077 | 92.308 | 23.077 | 346.154 | 415.385 | 761.538 | ||
| 53edo | 9:7:6 | 203.774 | 158.491 | 135.849 | 339.623 | 362.264 | 701.887 | |
| 9:8:5 | 203.774 | 181.132 | 113.208 | 316.981 | 384.906 | 701.887 | 5-limit patent val | |
| 11:6:4 | 249.057 | 135.849 | 90.566 | 339.623 | 384.906 | 724.528 | ||
| 11:7:3 | 249.057 | 158.491 | 67.925 | 316.981 | 407.547 | 724.528 | ||
| 11:8:2 | 249.057 | 181.132 | 45.283 | 294.340 | 430.189 | 724.528 | ||
| 11:9:1 | 249.057 | 203.774 | 22.642 | 271.698 | 452.830 | 724.528 | ||
| 13:4:3 | 294.340 | 90.566 | 67.925 | 362.264 | 384.906 | 747.170 | ||
| 13:5:2 | 294.340 | 113.208 | 45.283 | 339.623 | 407.547 | 747.170 | ||
| 13:6:1 | 294.340 | 135.849 | 22.642 | 316.981 | 430.189 | 747.170 | ||
| 15:3:1 | 339.623 | 67.925 | 22.642 | 362.264 | 407.547 | 769.811 | ||
| 54edo | 10:7:5 | 222.222 | 155.556 | 111.111 | 333.333 | 377.778 | 711.111 | 5-limit patent val |
| 10:9:3 | 222.222 | 200.000 | 66.667 | 288.889 | 422.222 | 711.111 | ||
| 12:5:4 | 266.667 | 111.111 | 88.889 | 355.556 | 377.778 | 733.333 | ||
| 12:7:2 | 266.667 | 155.556 | 44.444 | 311.111 | 422.222 | 733.333 | ||
| 12:8:1 | 266.667 | 177.778 | 22.222 | 288.889 | 444.444 | 733.333 | ||
| 14:5:1 | 311.111 | 111.111 | 22.222 | 333.333 | 422.222 | 755.556 | ||
| 16:2:1 | 355.556 | 44.444 | 22.222 | 377.778 | 400.000 | 777.778 | ||
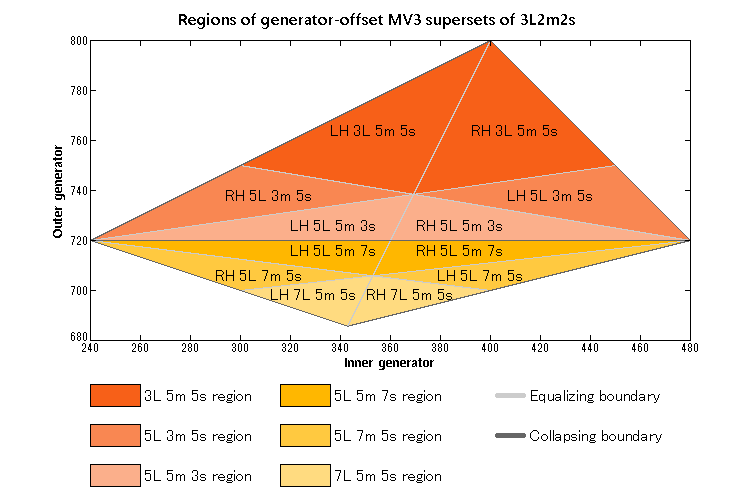
Supersets
Nicetone has following generator-offset MV3 supersets:
- Sephipechroid: 13-note 3L 5M 5s scale (LMsMLsMsLMsMs and LMsMLsMsMLsMs)
- Interoneichro: 13-note 5L 3M 5s scale (LMsLsLMsLsMLs and LMsLsMLsLsMLs)
- Sephimechroid: 13-note 5L 5M 3s scale (LMLMsLMLsMLMs and LMLsMLMLsMLMs)
- Beatloid: 17-note 5L 5M 7s scale (LMsLsMLsMsLMsLsMs and LMsLsMLsMsLsMLsMs)
- Enharoid: 17-note 5L 7M 5s scale (LMsLMsMLMsLMsMLsM and LMsLMsMLsMLMsMLsM)
- Moharoid: 17-note 7L 5M 5s scale (LMLsLMsLMLsMLsLMs and LMLsMLsLMLsMLsLMs)
Remarkable non-MV3 generator-offset supersets include blackdye (10-note, LmLsLmLsLs).
See also
- Blackdye – A 10-note scale that is an extension to nicetone.
- Zarlino – A 5-limit JI scale with the same pattern.
- Omnidiatonic – Sister 2L 3M 2s scale
- Antinicetone – Sister 2L 2M 3s scale
- 5L 2s – LM-equalized version of nicetone
- 5L 2s Muddles – Other diatonic muddles
- 3L 4s – MS-equalized version of nicetone
- 3L 2s – Collapsed version of nicetone