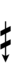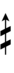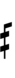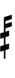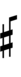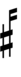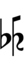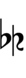37edo: Difference between revisions
→Links: Lumatone mapping |
m Text replacement - "Ups and Downs Notation" to "Ups and downs notation" |
||
| (45 intermediate revisions by 15 users not shown) | |||
| Line 6: | Line 6: | ||
}} | }} | ||
{{Infobox ET}} | {{Infobox ET}} | ||
{{ | {{ED intro}} | ||
== Theory == | == Theory == | ||
37edo | 37edo has very accurate approximations of harmonics [[5/1|5]], [[7/1|7]], [[11/1|11]] and [[13/1|13]], making it a good choice for a [[no-threes subgroup temperaments|no-threes]] approach. Harmonic 11 is particularly accurate, being only 0.03 cents sharp. | ||
Using its best (and sharp) fifth, 37edo tempers out 250/243, making it a variant of [[porcupine]] temperament. It is the [[optimal patent val]] for [[Porcupine family #Porcupinefish|porcupinefish]], which is about as accurate as 13-limit porcupine extensions will be. Using its alternative flat fifth, it tempers out [[16875/16384]], making it a [[negri]] tuning. It also tempers out 2187/2000, resulting in a temperament where three minor whole tones make up a fifth ([[gorgo]]/[[laconic]]). | Using its best (and sharp) fifth, 37edo tempers out 250/243, making it a variant of [[porcupine]] temperament. It is the [[optimal patent val]] for [[Porcupine family #Porcupinefish|porcupinefish]], which is about as accurate as 13-limit porcupine extensions will be. Using its alternative flat fifth, it tempers out [[16875/16384]], making it a [[negri]] tuning. It also tempers out 2187/2000, resulting in a temperament where three minor whole tones make up a fifth ([[gorgo]]/[[laconic]]). | ||
37edo is also a very accurate equal tuning for [[undecimation]] temperament, which has a [[generator]] of about 519 cents; 2 generators lead to 29/16; 3 generators to 32/13; 6 generators to a 10 cent sharp 6/1; 8 generators to a very accurate 11/1 and 10 generators to 20/1. It has a [[7L 2s]] enneatonic [[mos]], which in 37edo scale degrees is 0, 1, 6, 11, 16, 17, 22, 27, 32, a scale structure reminiscent of mavila; as well as a 16-note mos. | 37edo is also a very accurate equal tuning for [[undecimation]] temperament, which has a [[generator]] of about 519 cents; 2 generators lead to 29/16; 3 generators to 32/13; 6 generators to a 10 cent sharp 6/1; 8 generators to a very accurate 11/1 and 10 generators to 20/1. It has a [[7L 2s]] enneatonic [[mos]], which in 37edo scale degrees is 0, 1, 6, 11, 16, 17, 22, 27, 32, a scale structure reminiscent of mavila; as well as a 16-note mos. | ||
In the no-3 [[13-odd-limit]], 37edo maintains the smallest relative error of any edo until [[851edo]], and the smallest absolute error until [[103edo]]{{clarify}}. <!-- what is the metric being used? --> | |||
=== Odd harmonics === | === Odd harmonics === | ||
| Line 59: | Line 61: | ||
37edo has great potential as a near-just xenharmonic system, with high-prime chords such as 8:10:11:13:14 with no perfect fifths available for common terrestrial progressions. The 9/8 approximation is usable but introduces error. One may choose to treat either of the intervals close to 3/2 as 3/2, introducing additional approximations with considerable error (see interval table below). | 37edo has great potential as a near-just xenharmonic system, with high-prime chords such as 8:10:11:13:14 with no perfect fifths available for common terrestrial progressions. The 9/8 approximation is usable but introduces error. One may choose to treat either of the intervals close to 3/2 as 3/2, introducing additional approximations with considerable error (see interval table below). | ||
=== No-3 approach === | |||
If prime 3 is ignored, 37edo represents the no-3 23-odd-limit consistently, and is distinctly consistent within the no-3 16-integer-limit. | |||
== Intervals == | == Intervals == | ||
{| class="wikitable center-1 right-2" | {| class="wikitable center-1 right-2" | ||
|- | |- | ||
| Line 94: | Line 98: | ||
| 3 | | 3 | ||
| 97.30 | | 97.30 | ||
| [[55/52]] | | [[128/121]], [[55/52]] | ||
| [[16/15]] | | [[16/15]] | ||
| | | | ||
| Line 311: | Line 315: | ||
| 34 | | 34 | ||
| 1102.70 | | 1102.70 | ||
| [[104/55]] | | [[121/64]], [[104/55]] | ||
| [[15/8]] | | [[15/8]] | ||
| | | | ||
| Line 339: | Line 343: | ||
== Notation == | == Notation == | ||
=== Ups and downs notation === | |||
37edo can be notated using [[ups and downs notation]]: | |||
{| class="wikitable center-all right-2 left-3" | {| class="wikitable center-all right-2 left-3" | ||
|- | |- | ||
! Degrees | ! Degrees | ||
! Cents | ! Cents | ||
! colspan="3" | [[Ups and | ! colspan="3" | [[Ups and downs notation]] | ||
|- | |- | ||
| 0 | | 0 | ||
| Line 573: | Line 580: | ||
| D | | D | ||
|} | |} | ||
37edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc. | |||
{{Sharpness-sharp6a}} | |||
Half-sharps and half-flats can be used to avoid triple arrows: | |||
{{Sharpness-sharp6b}} | |||
[[Alternative symbols for ups and downs notation#Sharp-6| Alternative ups and downs]] have sharps and flats with arrows borrowed from extended [[Helmholtz–Ellis notation]]: | |||
{{Sharpness-sharp6}} | |||
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals: | |||
{{Sharpness-sharp6-qt}} | |||
=== Ivan Wyschnegradsky's notation === | |||
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from [[72edo]] can also be used: | |||
{{Sharpness-sharp6-iw}} | |||
=== Sagittal notation === | |||
This notation uses the same sagittal sequence as EDOs [[23edo#Second-best fifth notation|23b]], [[30edo#Sagittal notation|30]], and [[44edo#Sagittal notation|44]]. | |||
==== Evo and Revo flavors ==== | |||
<imagemap> | |||
File:37-EDO_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 599 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]] | |||
default [[File:37-EDO_Sagittal.svg]] | |||
</imagemap> | |||
==== Alternative Evo flavor ==== | |||
<imagemap> | |||
File:37-EDO_Alternative_Evo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 639 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]] | |||
default [[File:37-EDO_Alternative_Evo_Sagittal.svg]] | |||
</imagemap> | |||
==== Evo-SZ flavor ==== | |||
<imagemap> | |||
File:37-EDO_Evo-SZ_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 623 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]] | |||
default [[File:37-EDO_Evo-SZ_Sagittal.svg]] | |||
</imagemap> | |||
== Regular temperament properties == | == Regular temperament properties == | ||
{| class="wikitable center-4 center-5 center-6" | {| class="wikitable center-4 center-5 center-6" | ||
! rowspan="2" | Subgroup | |- | ||
! rowspan="2" | [[Subgroup]] | |||
! rowspan="2" | [[Comma list]] | ! rowspan="2" | [[Comma list]] | ||
! rowspan="2" | [[Mapping]] | ! rowspan="2" | [[Mapping]] | ||
| Line 587: | Line 645: | ||
| 2.5 | | 2.5 | ||
| {{monzo| 86 -37 }} | | {{monzo| 86 -37 }} | ||
| | | {{mapping| 37 86 }} | ||
| | | −0.619 | ||
| 0.619 | | 0.619 | ||
| 1.91 | | 1.91 | ||
| Line 594: | Line 652: | ||
| 2.5.7 | | 2.5.7 | ||
| 3136/3125, 4194304/4117715 | | 3136/3125, 4194304/4117715 | ||
| | | {{mapping| 37 86 104 }} | ||
| | | −0.905 | ||
| 0.647 | | 0.647 | ||
| 2.00 | | 2.00 | ||
| Line 601: | Line 659: | ||
| 2.5.7.11 | | 2.5.7.11 | ||
| 176/175, 1375/1372, 65536/65219 | | 176/175, 1375/1372, 65536/65219 | ||
| | | {{mapping| 37 86 104 128 }} | ||
| | | −0.681 | ||
| 0.681 | | 0.681 | ||
| 2.10 | | 2.10 | ||
| Line 608: | Line 666: | ||
| 2.5.7.11.13 | | 2.5.7.11.13 | ||
| 176/175, 640/637, 847/845, 1375/1372 | | 176/175, 640/637, 847/845, 1375/1372 | ||
| | | {{mapping| 37 86 104 128 137 }} | ||
| | | −0.692 | ||
| 0.610 | | 0.610 | ||
| 1.88 | | 1.88 | ||
|} | |} | ||
* 37et is most prominent in the no-3 11-, 13-, 17-, 19- and 23-limit subgroups. The next equal temperaments doing better in these subgroups are 109, 581, 103, 124 and 93, respectively. | |||
* 37et is most prominent in the no-3 11-, 13-, 17-, 19- and 23-limit subgroups. The next | |||
=== Rank-2 temperaments === | === Rank-2 temperaments === | ||
| Line 646: | Line 703: | ||
|- | |- | ||
| 6\37 | | 6\37 | ||
| colspan="2" | [[Didacus]] / [[ | | colspan="2" | [[Didacus]] / [[roulette]] | ||
|- | |- | ||
| 7\37 | | 7\37 | ||
| [[ | | [[Shoe]] / [[semaja]] | ||
| [[ | | [[Shoe]] / [[laconic]] / [[gorgo]] | ||
|- | |- | ||
| 8\37 | | 8\37 | ||
| Line 658: | Line 715: | ||
| 9\37 | | 9\37 | ||
| | | | ||
| [[ | | [[Gariberttet]] | ||
|- | |- | ||
| 10\37 | | 10\37 | ||
| Line 681: | Line 738: | ||
|- | |- | ||
| 15\37 | | 15\37 | ||
| [[ | | [[Ultrapyth]], [[oceanfront]] | ||
| | | | ||
|- | |- | ||
| Line 699: | Line 756: | ||
== Scales == | == Scales == | ||
* [[MOS Scales of 37edo]] | * [[MOS Scales of 37edo]] | ||
* [[ | * [[Chromatic pairs#Roulette|Roulette scales]] | ||
* [[37ED4]] | * [[37ED4]] | ||
* [[Square root of 13 over 10]] | * [[Square root of 13 over 10]] | ||
=== Every 8 steps of 37edo === | |||
{| class="wikitable center-1 right-2" | |||
|+ | |||
!Degrees | |||
!Cents | |||
!Approximate Ratios<br>of 6.7.11.20.27 subgroup | |||
!Additional Ratios | |||
|- | |||
|0 | |||
|0.000 | |||
|[[1/1]] | |||
| | |||
|- | |||
|1 | |||
|259.46 | |||
|[[7/6]] | |||
| | |||
|- | |||
|2 | |||
|518.92 | |||
|[[27/20]] | |||
| | |||
|- | |||
|3 | |||
|778.38 | |||
|[[11/7]] | |||
| | |||
|- | |||
|4 | |||
|1037.84 | |||
|[[20/11]], [[11/6]] | |||
| | |||
|- | |||
|5 | |||
|1297.30 | |||
| | |||
|[[19/9]] | |||
|- | |||
|6 | |||
|1556.76 | |||
|[[27/11]] | |||
| | |||
|- | |||
|7 | |||
|1816.22 | |||
|[[20/7]] | |||
| | |||
|- | |||
|8 | |||
|2075.68 | |||
|[[10/3]] | |||
| | |||
|- | |||
|9 | |||
|2335.14 | |||
|[[27/7]] | |||
| | |||
|- | |||
|10 | |||
|2594.59 | |||
|[[9/2]] | |||
| | |||
|- | |||
|11 | |||
|2854.05 | |||
| | |||
|[[26/5]] | |||
|- | |||
|12 | |||
|3113.51 | |||
|[[6/1]] | |||
| | |||
|- | |||
|13 | |||
|3372.97 | |||
|[[7/1]] | |||
| | |||
|- | |||
|14 | |||
|3632.43 | |||
| | |||
| | |||
|- | |||
|15 | |||
|3891.89 | |||
| | |||
|[[19/2]] | |||
|- | |||
|16 | |||
|4151.35 | |||
|[[11/1]] | |||
| | |||
|- | |||
|17 | |||
|4410.81 | |||
| | |||
| | |||
|- | |||
|18 | |||
|4670.27 | |||
| | |||
| | |||
|- | |||
|19 | |||
|4929.73 | |||
| | |||
| | |||
|- | |||
|20 | |||
|5189.19 | |||
|[[20/1]] | |||
| | |||
|- | |||
|21 | |||
|5448.65 | |||
| | |||
| | |||
|- | |||
|22 | |||
|5708.11 | |||
|[[27/1]] | |||
| | |||
|} | |||
== Instruments == | |||
; Lumatone | |||
* [[Lumatone mapping for 37edo]] | |||
; Fretted instruments | |||
* [[Skip fretting system 37 2 7]] | |||
== Music == | == Music == | ||
| Line 710: | Line 896: | ||
* [https://www.youtube.com/watch?v=IULi2zSdatA ''Mindless vibe''] (2023) | * [https://www.youtube.com/watch?v=IULi2zSdatA ''Mindless vibe''] (2023) | ||
; [[ | ; [[Bryan Deister]] | ||
* [https://www.youtube.com/shorts/e7dLJTsS3PQ ''37edo''] (2025) | |||
* [https://www.youtube.com/shorts/m9hmiH8zong ''37edo jam''] (2025) | |||
; [[Francium]] | |||
* [https://www.youtube.com/watch?v=jpPjVouoq3E ''5 days in''] (2023) | * [https://www.youtube.com/watch?v=jpPjVouoq3E ''5 days in''] (2023) | ||
* [https://www.youtube.com/watch?v=ngxSiuVadls ''A Dark Era Arises''] (2023) – | * [https://www.youtube.com/watch?v=ngxSiuVadls ''A Dark Era Arises''] (2023) – in Porcupine[15], 37edo tuning | ||
* [https://www.youtube.com/watch?v=U93XFJJ1aXw ''Two Faced People''] (2025) – in Twothirdtonic[10], 37edo tuning | |||
; [[Andrew Heathwaite]] | ; [[Andrew Heathwaite]] | ||
* [https://andrewheathwaite.bandcamp.com/track/shorn-brown "Shorn Brown"] from ''Newbeams'' (2012) | * [https://andrewheathwaite.bandcamp.com/track/shorn-brown "Shorn Brown"] from ''Newbeams'' (2012) | ||
* [https://andrewheathwaite.bandcamp.com/track/jellybear "Jellybear"] from ''Newbeams'' (2012) | * [https://andrewheathwaite.bandcamp.com/track/jellybear "Jellybear"] from ''Newbeams'' (2012) | ||
; [[Aaron Krister Johnson]] | ; [[Aaron Krister Johnson]] | ||
| Line 723: | Line 914: | ||
; [[JUMBLE]] | ; [[JUMBLE]] | ||
* [https://www.youtube.com/watch?v=taT1DClJ2KM ''Tyrian and Gold''] (2024) | * [https://www.youtube.com/watch?v=taT1DClJ2KM ''Tyrian and Gold''] (2024) | ||
; [[User:Fitzgerald Lee|Fitzgerald Lee]] | |||
* [https://www.youtube.com/watch?v=Nr0cUJcL4SU ''Bittersweet End''] (2025) | |||
; [[Mandrake]] | ; [[Mandrake]] | ||
| Line 730: | Line 924: | ||
* [https://www.youtube.com/watch?v=7dU8eyGbt9I ''Deck The Halls''] (2022) | * [https://www.youtube.com/watch?v=7dU8eyGbt9I ''Deck The Halls''] (2022) | ||
* [https://www.youtube.com/watch?v=HTAobydvC20 Marcello - Bach: Adagio from BWV 974, arranged for Oboe & Organ, tuned into 37edo] (2022) | * [https://www.youtube.com/watch?v=HTAobydvC20 Marcello - Bach: Adagio from BWV 974, arranged for Oboe & Organ, tuned into 37edo] (2022) | ||
* [https://www.youtube.com/watch?v=hpjZZXFM_Fk ''Little Fugue on Happy Birthday''] (2022) – | * [https://www.youtube.com/watch?v=hpjZZXFM_Fk ''Little Fugue on Happy Birthday''] (2022) – in Passion, 37edo tuning | ||
* [https://www.youtube.com/watch?v=SgHY3snZ5bs ''Fugue on an Original Theme''] (2022) | * [https://www.youtube.com/watch?v=SgHY3snZ5bs ''Fugue on an Original Theme''] (2022) | ||
* [https://www.youtube.com/watch?v=AJ2sa-fRqbE Paradies, Toccata, Arranged for Organ and Tuned into 37edo] (2023) | * [https://www.youtube.com/watch?v=AJ2sa-fRqbE Paradies, Toccata, Arranged for Organ and Tuned into 37edo] (2023) | ||
| Line 736: | Line 930: | ||
; [[Micronaive]] | ; [[Micronaive]] | ||
* [https://youtu.be/TMVRYLvg_cA No.27.50] (2022) | * [https://youtu.be/TMVRYLvg_cA No.27.50] (2022) | ||
; [[Herman Miller]] | |||
* ''[https://soundcloud.com/morphosyntax-1/luck-of-the-draw Luck of the Draw]'' (2023) | |||
; [[Joseph Monzo]] | ; [[Joseph Monzo]] | ||
| Line 745: | Line 942: | ||
; [[Ray Perlner]] | ; [[Ray Perlner]] | ||
* [https://www.youtube.com/watch?v=8reCr2nDGbw ''Porcupine Lullaby''] (2020) – | * [https://www.youtube.com/watch?v=8reCr2nDGbw ''Porcupine Lullaby''] (2020) – in Porcupine, 37edo tuning | ||
* [https://www.youtube.com/watch?v=j8C9ECvfyQM ''Fugue for Brass in 37EDO sssLsss "Dingoian"''] (2022) – | * [https://www.youtube.com/watch?v=j8C9ECvfyQM ''Fugue for Brass in 37EDO sssLsss "Dingoian"''] (2022) – in Porcupine[7], 37edo tuning | ||
* [https://www.youtube.com/watch?v=_xfvNKUu8gY ''Fugue for Klezmer Band in 37EDO Porcupine<nowiki>[</nowiki>7<nowiki>]</nowiki> sssssLs "Lemurian"''] (2023) – | * [https://www.youtube.com/watch?v=_xfvNKUu8gY ''Fugue for Klezmer Band in 37EDO Porcupine<nowiki>[</nowiki>7<nowiki>]</nowiki> sssssLs "Lemurian"''] (2023) – in Porcupine[7], 37edo tuning | ||
; [[Phanomium]] | |||
* [https://www.youtube.com/watch?v=2otxZqUrvHc ''Elevated Floors''] (2025) | |||
* [https://www.youtube.com/watch?v=BbexOU-9700 ''cat jam 37''] (2025) | |||
; [[Togenom]] | |||
* "Canals of Mars" from ''Xenharmonics, Vol. 5'' (2024) – [https://open.spotify.com/track/7v2dpCjiRKUfVVBZw8aWSf Spotify] |[https://togenom.bandcamp.com/track/canals-of-mars Bandcamp] | [https://www.youtube.com/watch?v=qPcEl_bifC0 YouTube] | |||
== | ; [[Uncreative Name]] | ||
* [http://tonalsoft.com/enc/number/37-edo/37edo.aspx | * [https://www.youtube.com/watch?v=rE9L56yZ1Kw ''Winter''] (2025) | ||
; <nowiki>XENO*n*</nowiki> | |||
* ''[https://www.youtube.com/watch?v=_m5u4VviMXw Galantean Drift]'' (2025) | |||
== See also == | |||
* [[User:Unque/37edo Composition Theory|Unque's approach]] | |||
== External links == | |||
* [http://tonalsoft.com/enc/number/37-edo/37edo.aspx 37-edo / 37-et / 37-tone equal-temperament] on [[Tonalsoft Encyclopedia]] | |||
[[Category:Listen]] | [[Category:Listen]] | ||
Latest revision as of 01:07, 20 August 2025
| ← 36edo | 37edo | 38edo → |
37 equal divisions of the octave (abbreviated 37edo or 37ed2), also called 37-tone equal temperament (37tet) or 37 equal temperament (37et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 37 equal parts of about 32.4 ¢ each. Each step represents a frequency ratio of 21/37, or the 37th root of 2.
Theory
37edo has very accurate approximations of harmonics 5, 7, 11 and 13, making it a good choice for a no-threes approach. Harmonic 11 is particularly accurate, being only 0.03 cents sharp.
Using its best (and sharp) fifth, 37edo tempers out 250/243, making it a variant of porcupine temperament. It is the optimal patent val for porcupinefish, which is about as accurate as 13-limit porcupine extensions will be. Using its alternative flat fifth, it tempers out 16875/16384, making it a negri tuning. It also tempers out 2187/2000, resulting in a temperament where three minor whole tones make up a fifth (gorgo/laconic).
37edo is also a very accurate equal tuning for undecimation temperament, which has a generator of about 519 cents; 2 generators lead to 29/16; 3 generators to 32/13; 6 generators to a 10 cent sharp 6/1; 8 generators to a very accurate 11/1 and 10 generators to 20/1. It has a 7L 2s enneatonic mos, which in 37edo scale degrees is 0, 1, 6, 11, 16, 17, 22, 27, 32, a scale structure reminiscent of mavila; as well as a 16-note mos.
In the no-3 13-odd-limit, 37edo maintains the smallest relative error of any edo until 851edo, and the smallest absolute error until 103edo[clarification needed].
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +11.6 | +2.9 | +4.1 | -9.3 | +0.0 | +2.7 | +14.4 | -7.7 | -5.6 | +15.7 | -12.1 |
| Relative (%) | +35.6 | +8.9 | +12.8 | -28.7 | +0.1 | +8.4 | +44.5 | -23.6 | -17.3 | +48.4 | -37.2 | |
| Steps (reduced) |
59 (22) |
86 (12) |
104 (30) |
117 (6) |
128 (17) |
137 (26) |
145 (34) |
151 (3) |
157 (9) |
163 (15) |
167 (19) | |
Subsets and supersets
37edo is the 12th prime edo, following 31edo and coming before 41edo.
74edo, which doubles it, provides an alternative approximation to harmonic 3 that supports meantone. 111edo, which triples it, gives a very accurate approximation of harmonic 3, and manifests itself as a great higher-limit system. 296edo, which slices its step in eight, is a good 13-limit system.
Subgroups
37edo offers close approximations to harmonics 5, 7, 11, and 13, and a usable approximation of 9 as well.
- 12\37 = 389.2 cents
- 30\37 = 973.0 cents
- 17\37 = 551.4 cents
- 26\37 = 843.2 cents
- [6\37 = 194.6 cents]
This means 37 is quite accurate on the 2.5.7.11.13 subgroup, where it shares the same tuning as 111edo. In fact, on the larger 3*37 subgroup 2.27.5.7.11.13.51.57 subgroup not only shares the same tuning as 19-limit 111edo, it tempers out the same commas. A simpler but less accurate approach is to use the 2*37-subgroup, 2.9.7.11.13.17.19, on which it has the same tuning and commas as 74edo.
Dual fifths
The just perfect fifth of frequency ratio 3:2 is not well-approximated, and falls between two intervals in 37edo:
The flat fifth is 21\37 = 681.1 cents (37b val)
The sharp fifth is 22\37 = 713.5 cents
21\37 generates an anti-diatonic, or mavila, scale: 5 5 6 5 5 5 6
"minor third" = 10\37 = 324.3 cents
"major third" = 11\37 = 356.8 cents
22\37 generates an extreme superpythagorean scale: 7 7 1 7 7 7 1
"minor third" = 8\37 = 259.5 cents
"major third" = 14\37 = 454.1 cents
If the minor third of 259.5 cents is mapped to 7/6, this superpythagorean scale can be thought of as a variant of Oceanfront temperament.
37edo can only barely be considered as "dual-fifth", because the sharp fifth is 12 cents sharp of 3/2, has a regular diatonic scale, and can be interpreted as somewhat accurate regular temperaments like archy and the aforementioned oceanfront. In contrast, the flat fifth is 21 cents flat and the only low-limit interpretation is as the very inaccurate mavila.
Since both fifths do not support meantone, the "major thirds" of both systems are not 12\37 = 389.2¢, the closest approximation to 5/4 available in 37edo.
37edo has great potential as a near-just xenharmonic system, with high-prime chords such as 8:10:11:13:14 with no perfect fifths available for common terrestrial progressions. The 9/8 approximation is usable but introduces error. One may choose to treat either of the intervals close to 3/2 as 3/2, introducing additional approximations with considerable error (see interval table below).
No-3 approach
If prime 3 is ignored, 37edo represents the no-3 23-odd-limit consistently, and is distinctly consistent within the no-3 16-integer-limit.
Intervals
| Degrees | Cents | Approximate Ratios of 2.5.7.11.13.27 subgroup |
Additional Ratios of 3 with a sharp 3/2 |
Additional Ratios of 3 with a flat 3/2 |
Additional Ratios of 9 with 194.59¢ 9/8 |
|---|---|---|---|---|---|
| 0 | 0.00 | 1/1 | |||
| 1 | 32.43 | 55/54, 56/55 | |||
| 2 | 64.86 | 27/26, 28/27 | |||
| 3 | 97.30 | 128/121, 55/52 | 16/15 | ||
| 4 | 129.73 | 14/13 | 13/12, 15/14 | 12/11 | |
| 5 | 162.16 | 11/10 | 10/9, 12/11 | 13/12 | |
| 6 | 194.59 | 28/25 | 9/8, 10/9 | ||
| 7 | 227.03 | 8/7 | 9/8 | ||
| 8 | 259.46 | 7/6, 15/13 | |||
| 9 | 291.89 | 13/11, 32/27 | 6/5, 7/6 | ||
| 10 | 324.32 | 6/5, 11/9 | |||
| 11 | 356.76 | 16/13, 27/22 | 11/9 | ||
| 12 | 389.19 | 5/4 | |||
| 13 | 421.62 | 14/11, 32/25 | 9/7 | ||
| 14 | 454.05 | 13/10 | 9/7 | ||
| 15 | 486.49 | 4/3 | |||
| 16 | 518.92 | 27/20 | 4/3 | ||
| 17 | 551.35 | 11/8 | 15/11 | 18/13 | |
| 18 | 583.78 | 7/5 | 18/13 | ||
| 19 | 616.22 | 10/7 | 13/9 | ||
| 20 | 648.65 | 16/11 | 22/15 | 13/9 | |
| 21 | 681.08 | 40/27 | 3/2 | ||
| 22 | 713.51 | 3/2 | |||
| 23 | 745.95 | 20/13 | 14/9 | ||
| 24 | 778.38 | 11/7, 25/16 | 14/9 | ||
| 25 | 810.81 | 8/5 | |||
| 26 | 843.24 | 13/8, 44/27 | 18/11 | ||
| 27 | 875.68 | 5/3, 18/11 | |||
| 28 | 908.11 | 22/13, 27/16 | 5/3, 12/7 | ||
| 29 | 940.54 | 12/7, 26/15 | |||
| 30 | 972.97 | 7/4 | 16/9 | ||
| 31 | 1005.41 | 25/14 | 16/9, 9/5 | ||
| 32 | 1037.84 | 20/11 | 9/5, 11/6 | ||
| 33 | 1070.27 | 13/7 | 24/13, 28/15 | 11/6 | |
| 34 | 1102.70 | 121/64, 104/55 | 15/8 | ||
| 35 | 1135.14 | 27/14, 52/27 | |||
| 36 | 1167.57 | ||||
| 37 | 1200.00 | 2/1 |
Notation
Ups and downs notation
37edo can be notated using ups and downs notation:
| Degrees | Cents | Ups and downs notation | ||
|---|---|---|---|---|
| 0 | 0.00 | Perfect 1sn | P1 | D |
| 1 | 32.43 | Minor 2nd | m2 | Eb |
| 2 | 64.86 | Upminor 2nd | ^m2 | ^Eb |
| 3 | 97.30 | Downmid 2nd | v~2 | ^^Eb |
| 4 | 129.73 | Mid 2nd | ~2 | Ed |
| 5 | 162.16 | Upmid 2nd | ^~2 | vvE |
| 6 | 194.59 | Downmajor 2nd | vM2 | vE |
| 7 | 227.03 | Major 2nd | M2 | E |
| 8 | 259.46 | Minor 3rd | m3 | F |
| 9 | 291.89 | Upminor 3rd | ^m3 | ^F |
| 10 | 324.32 | Downmid 3rd | v~3 | ^^F |
| 11 | 356.76 | Mid 3rd | ~3 | Ft |
| 12 | 389.19 | Upmid 3rd | ^~3 | vvF# |
| 13 | 421.62 | Downmajor 3rd | vM3 | vF# |
| 14 | 454.05 | Major 3rd | M3 | F# |
| 15 | 486.49 | Perfect 4th | P4 | G |
| 16 | 518.92 | Up 4th, Dim 5th | ^4, d5 | ^G, Ab |
| 17 | 551.35 | Downmid 4th, Updim 5th | v~4, ^d5 | ^^G, ^Ab |
| 18 | 583.78 | Mid 4th, Downmid 5th | ~4, v~5 | Gt, ^^Ab |
| 19 | 616.22 | Mid 5th, Upmid 4th | ~5, ^~4 | Ad, vvG# |
| 20 | 648.65 | Upmid 5th, Downaug 5th | ^~5, vA4 | vvA, vG# |
| 21 | 681.08 | Down 5th, Aug 4th | v5, A4 | vA, G# |
| 22 | 713.51 | Perfect 5th | P5 | A |
| 23 | 745.95 | Minor 6th | m6 | Bb |
| 24 | 778.38 | Upminor 6th | ^m6 | ^Bb |
| 25 | 810.81 | Downmid 6th | v~6 | ^^Bb |
| 26 | 843.24 | Mid 6th | ~6 | Bd |
| 27 | 875.68 | Upmid 6th | ^~6 | vvB |
| 28 | 908.11 | Downmajor 6th | vM6 | vB |
| 29 | 940.54 | Major 6th | M6 | B |
| 30 | 972.97 | Minor 7th | m7 | C |
| 31 | 1005.41 | Upminor 7th | ^m7 | ^C |
| 32 | 1037.84 | Downmid 7th | v~7 | ^^C |
| 33 | 1070.27 | Mid 7th | ~7 | Ct |
| 34 | 1102.70 | Upmid 7th | ^~7 | vvC# |
| 35 | 1135.14 | Downmajor 7th | vM7 | vC# |
| 36 | 1167.57 | Major 7th | M7 | C# |
| 37 | 1200.00 | Perfect 8ve | P8 | D |
37edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Half-sharps and half-flats can be used to avoid triple arrows:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Alternative ups and downs have sharps and flats with arrows borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
Ivan Wyschnegradsky's notation
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
Sagittal notation
This notation uses the same sagittal sequence as EDOs 23b, 30, and 44.
Evo and Revo flavors

Alternative Evo flavor

Evo-SZ flavor

Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.5 | [86 -37⟩ | [⟨37 86]] | −0.619 | 0.619 | 1.91 |
| 2.5.7 | 3136/3125, 4194304/4117715 | [⟨37 86 104]] | −0.905 | 0.647 | 2.00 |
| 2.5.7.11 | 176/175, 1375/1372, 65536/65219 | [⟨37 86 104 128]] | −0.681 | 0.681 | 2.10 |
| 2.5.7.11.13 | 176/175, 640/637, 847/845, 1375/1372 | [⟨37 86 104 128 137]] | −0.692 | 0.610 | 1.88 |
- 37et is most prominent in the no-3 11-, 13-, 17-, 19- and 23-limit subgroups. The next equal temperaments doing better in these subgroups are 109, 581, 103, 124 and 93, respectively.
Rank-2 temperaments
| Generator | In patent val | In 37b val |
|---|---|---|
| 1\37 | ||
| 2\37 | Sycamore | |
| 3\37 | Passion | |
| 4\37 | Twothirdtonic | Negri |
| 5\37 | Porcupine / porcupinefish | |
| 6\37 | Didacus / roulette | |
| 7\37 | Shoe / semaja | Shoe / laconic / gorgo |
| 8\37 | Semaphore (37bd) | |
| 9\37 | Gariberttet | |
| 10\37 | Orgone | |
| 11\37 | Beatles | |
| 12\37 | Würschmidt (out-of-tune) | |
| 13\37 | Skwares (37dd) | |
| 14\37 | Ammonite | |
| 15\37 | Ultrapyth, oceanfront | |
| 16\37 | Undecimation | |
| 17\37 | Freivald, emka, onzonic | |
| 18\37 | ||
Scales
Every 8 steps of 37edo
| Degrees | Cents | Approximate Ratios of 6.7.11.20.27 subgroup |
Additional Ratios |
|---|---|---|---|
| 0 | 0.000 | 1/1 | |
| 1 | 259.46 | 7/6 | |
| 2 | 518.92 | 27/20 | |
| 3 | 778.38 | 11/7 | |
| 4 | 1037.84 | 20/11, 11/6 | |
| 5 | 1297.30 | 19/9 | |
| 6 | 1556.76 | 27/11 | |
| 7 | 1816.22 | 20/7 | |
| 8 | 2075.68 | 10/3 | |
| 9 | 2335.14 | 27/7 | |
| 10 | 2594.59 | 9/2 | |
| 11 | 2854.05 | 26/5 | |
| 12 | 3113.51 | 6/1 | |
| 13 | 3372.97 | 7/1 | |
| 14 | 3632.43 | ||
| 15 | 3891.89 | 19/2 | |
| 16 | 4151.35 | 11/1 | |
| 17 | 4410.81 | ||
| 18 | 4670.27 | ||
| 19 | 4929.73 | ||
| 20 | 5189.19 | 20/1 | |
| 21 | 5448.65 | ||
| 22 | 5708.11 | 27/1 |
Instruments
- Lumatone
- Fretted instruments
Music
- Mindless vibe (2023)
- 5 days in (2023)
- A Dark Era Arises (2023) – in Porcupine[15], 37edo tuning
- Two Faced People (2025) – in Twothirdtonic[10], 37edo tuning
- "Shorn Brown" from Newbeams (2012)
- "Jellybear" from Newbeams (2012)
- Tyrian and Gold (2024)
- Bittersweet End (2025)
- What if? (2023)
- Deck The Halls (2022)
- Marcello - Bach: Adagio from BWV 974, arranged for Oboe & Organ, tuned into 37edo (2022)
- Little Fugue on Happy Birthday (2022) – in Passion, 37edo tuning
- Fugue on an Original Theme (2022)
- Paradies, Toccata, Arranged for Organ and Tuned into 37edo (2023)
- No.27.50 (2022)
- Luck of the Draw (2023)
- The Kog Sisters (2014)
- Afrikan Song (2016)
- Porcupine Lullaby (2020) – in Porcupine, 37edo tuning
- Fugue for Brass in 37EDO sssLsss "Dingoian" (2022) – in Porcupine[7], 37edo tuning
- Fugue for Klezmer Band in 37EDO Porcupine[7] sssssLs "Lemurian" (2023) – in Porcupine[7], 37edo tuning
- Elevated Floors (2025)
- cat jam 37 (2025)
- Winter (2025)
- XENO*n*
- Galantean Drift (2025)