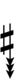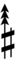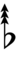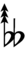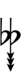63edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Wikispaces>iamcamtaylor
**Imported revision 586694489 - Original comment: **
→Rank-2 temperaments: 81/80 can't be the associated ratio for 1\63 in Sevond, because 63edo maps 81/80 inconsistently to 2\63; I think 64/63 fits the bill, but better check on that
 
(62 intermediate revisions by 19 users not shown)
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
{{Infobox ET}}
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
{{ED intro}}
: This revision was by author [[User:iamcamtaylor|iamcamtaylor]] and made on <tt>2016-07-08 01:06:56 UTC</tt>.<br>
: The original revision id was <tt>586694489</tt>.<br>
: The revision comment was: <tt></tt><br>
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">The 63 equal division divides the octave into 63 equal parts of 19.048 cents each. It tempers out 3125/3072 in the 5-limit and 875/864, 225/224 and 245/243 in the 7-limit, so that it supports magic temperament. In the 11-limit it tempers out 100/99, supporting 11-limit magic, plus 896/891, 385/384 and 640/539. In the 13-limit it tempers put 275/273, 169/168, 640/637, 352/351, 364/363 and 676/675. It provides the optimal patent val for the 29&amp;63 temperament in the 7-, 11- and 13-limit. It is divisible by 3, 7, 9 and 21.


63 is also a fascinating division to look at in the 23-limit, as its regular augmented fourth (+6 fifths) is less than 0.3c sharp of 23/16, therefore tempering out 729/726. Although it doesn't deal as well with primes 5, 17, and 19, it excels in the 2.3.7.11.13.23 group, and is a great candidate for a rank-1 or rank-2 gentle tuning. As a fifths-system, the diesis after 12 fifths can represent 32:33, 27:28, 88:91, and more, making chains of fifths 12 or longer very useful in covering harmonic and melodic ground while providing a lot of different colour in different keys. A 17-tone fifths chain looks on the surface a little similar to 17edo, but as -17 fifths gets us to 64/63, observing the comma becomes an essential part in progressions favouring prime 7.
== Theory ==
63edo is almost [[consistent]] to the [[15-odd-limit]]; the only inconsistency is that [[10/9]] is mapped to 9\63 (1\7, the same as what [[11/10]] is mapped to consistently) so that it is almost 11{{cent}} out of tune. This corresponds to 63edo exaggerating the syntonic comma, [[81/80]], to two steps, so that it finds a somewhat flat mean-tone between ~10/9 and ~9/8.  


As an equal temperament, it [[tempering out|tempers out]] [[3125/3072]] in the 5-limit and [[225/224]], [[245/243]], and [[875/864]] in the 7-limit, so that it [[support]]s [[magic]] temperament. In the 11-limit it tempers out [[100/99]], supporting 11-limit magic, plus [[385/384]] and [[540/539]], [[896/891]]. In the 13-limit it tempers out [[169/168]], [[275/273]], [[640/637]], [[352/351]], [[364/363]] and [[676/675]]. It provides the [[optimal patent val]] for [[immune]], the {{nowrap| 29 & 34d }} temperament in the 7-, 11- and 13-limit.


Audio:
63 is also a fascinating division to look at in the [[47-limit]]. Although it does not deal as well with primes 5, 17, 19, 37 and 41, it excels in the 2.3.7.11.13.23.29.31.43.47 [[subgroup]], and is a great candidate for a [[gentle]] tuning. Its regular augmented fourth (+6 fifths) is less than 0.3 cents sharp of [[23/16]], therefore tempering out [[736/729]]. Its diesis (+12 fifths) can represent [[33/32]], [[32/31]], [[30/29]], [[29/28]], [[28/27]], as well as [[91/88]], and more, so it is very versatile, making chains of fifths of 12 tones or longer very useful in covering harmonic and melodic ground while providing a lot of different colour in different keys. We can take advantage of the representation of 27:28:29:30:31:32:33, which splits [[11/9]] into six "small dieses" as a result; here it can be seen more clearly why these are not regular quarter-tones so are best distinguished from such with the qualifier "large", as otherwise we would expect to see some flavour of minor third after six of them.


https://soundcloud.com/camtaylor-1/63edobosanquetaxis-8thjuly2016-237111323-seconds-and-otonal-shifts
A 17-tone fifths chain looks on the surface a little similar to [[17edo]], but as −17 fifths gets us to [[64/63]], observing the comma becomes an essential part in progressions favouring prime 7. Furthermore, its prime 5 is far from unusable; although [[25/16]] is barely inconsistent, this affords the tuning supporting 7-limit magic, which may be considered interesting or desirable in of itself. And if this was not enough, if you really want to, it offers reasonable approximations to some yet higher primes too; namely [[43/32]], [[47/32]], and [[53/32]]; see the tables below.
https://soundcloud.com/cam-taylor-2-1/17-out-of-63edo-wurly-those-early-dreams
 
https://archive.org/details/17_63EDOEarlyDreamsTwo
=== Prime harmonics ===
https://soundcloud.com/cam-taylor-2-1/12tone63edo1</pre></div>
{{Harmonics in equal|63|columns=12}}
<h4>Original HTML content:</h4>
{{Harmonics in equal|63|start=13|columns=12|collapsed=1|title=Approximation of prime harmonics in 63edo (continued)}}
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;63edo&lt;/title&gt;&lt;/head&gt;&lt;body&gt;The 63 equal division divides the octave into 63 equal parts of 19.048 cents each. It tempers out 3125/3072 in the 5-limit and 875/864, 225/224 and 245/243 in the 7-limit, so that it supports magic temperament. In the 11-limit it tempers out 100/99, supporting 11-limit magic, plus 896/891, 385/384 and 640/539. In the 13-limit it tempers put 275/273, 169/168, 640/637, 352/351, 364/363 and 676/675. It provides the optimal patent val for the 29&amp;amp;63 temperament in the 7-, 11- and 13-limit. It is divisible by 3, 7, 9 and 21.&lt;br /&gt;
 
&lt;br /&gt;
=== Subsets and supersets ===
63 is also a fascinating division to look at in the 23-limit, as its regular augmented fourth (+6 fifths) is less than 0.3c sharp of 23/16, therefore tempering out 729/726. Although it doesn't deal as well with primes 5, 17, and 19, it excels in the 2.3.7.11.13.23 group, and is a great candidate for a rank-1 or rank-2 gentle tuning. As a fifths-system, the diesis after 12 fifths can represent 32:33, 27:28, 88:91, and more, making chains of fifths 12 or longer very useful in covering harmonic and melodic ground while providing a lot of different colour in different keys. A 17-tone fifths chain looks on the surface a little similar to 17edo, but as -17 fifths gets us to 64/63, observing the comma becomes an essential part in progressions favouring prime 7.&lt;br /&gt;
Since 63 factors into primes as {{nowrap| 3<sup>2</sup> × 7 }}, 63edo has subset edos {{EDOs| 3, 7, 9, and 21 }}.
&lt;br /&gt;
 
&lt;br /&gt;
Its representation of the 2.3.5.7.13 subgroup (no-11's 13-limit) can uniquely be described in terms of accurate approximations contained in its main subsets of [[7edo]] and [[9edo]]:
Audio:&lt;br /&gt;
* 1\9 = [[14/13]]~[[13/12]], implying the much more accurate 2\9 = ~[[7/6]] ([[septiennealic]])
&lt;br /&gt;
* 2\7 = [[39/32]]~[[128/105]], via [[4096/4095]] and the [[akjaysma]] (which are naturally paired)
&lt;!-- ws:start:WikiTextUrlRule:10:https://soundcloud.com/camtaylor-1/63edobosanquetaxis-8thjuly2016-237111323-seconds-and-otonal-shifts --&gt;&lt;a class="wiki_link_ext" href="https://soundcloud.com/camtaylor-1/63edobosanquetaxis-8thjuly2016-237111323-seconds-and-otonal-shifts" rel="nofollow"&gt;https://soundcloud.com/camtaylor-1/63edobosanquetaxis-8thjuly2016-237111323-seconds-and-otonal-shifts&lt;/a&gt;&lt;!-- ws:end:WikiTextUrlRule:10 --&gt;&lt;br /&gt;
If we avoid equating 14/13 and 13/12 (which is by far the highest damage equivalence) so that we achieve {{nowrap| 7/6 {{=}} 2\9 }} directly, we get the {{nowrap| 63 & 441 }} microtemperament in the same subgroup.
&lt;!-- ws:start:WikiTextUrlRule:11:https://soundcloud.com/cam-taylor-2-1/17-out-of-63edo-wurly-those-early-dreams --&gt;&lt;a class="wiki_link_ext" href="https://soundcloud.com/cam-taylor-2-1/17-out-of-63edo-wurly-those-early-dreams" rel="nofollow"&gt;https://soundcloud.com/cam-taylor-2-1/17-out-of-63edo-wurly-those-early-dreams&lt;/a&gt;&lt;!-- ws:end:WikiTextUrlRule:11 --&gt;&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextUrlRule:12:https://archive.org/details/17_63EDOEarlyDreamsTwo --&gt;&lt;a class="wiki_link_ext" href="https://archive.org/details/17_63EDOEarlyDreamsTwo" rel="nofollow"&gt;https://archive.org/details/17_63EDOEarlyDreamsTwo&lt;/a&gt;&lt;!-- ws:end:WikiTextUrlRule:12 --&gt;&lt;br /&gt;
== Intervals ==
&lt;!-- ws:start:WikiTextUrlRule:13:https://soundcloud.com/cam-taylor-2-1/12tone63edo1 --&gt;&lt;a class="wiki_link_ext" href="https://soundcloud.com/cam-taylor-2-1/12tone63edo1" rel="nofollow"&gt;https://soundcloud.com/cam-taylor-2-1/12tone63edo1&lt;/a&gt;&lt;!-- ws:end:WikiTextUrlRule:13 --&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>
{| class="wikitable center-all right-2 left-3"
|-
! Degree
! Cents
! Approximate ratios*
|-
| 0
| 0.0
| [[1/1]]
|-
| 1
| 19.0
| ''[[50/49]]'', ''[[55/54]]'', [[64/63]], [[65/64]], [[91/90]], [[105/104]]
|-
| 2
| 38.1
| [[45/44]], [[46/45]], [[49/48]], ''[[56/55]]'', ''[[66/65]]'', ''[[81/80]]''
|-
| 3
| 57.1
| ''[[25/24]]'', [[28/27]], [[29/28]], [[30/29]], [[31/30]], [[32/31]], [[33/32]], [[36/35]]
|-
| 4
| 76.2
| [[22/21]], [[23/22]], [[24/23]], [[26/25]], ''[[27/26]]''
|-
| 5
| 95.2
| ''[[21/20]]'', [[35/33]]
|-
| 6
| 114.3
| [[15/14]], [[16/15]]
|-
| 7
| 133.3
| [[13/12]], [[14/13]]
|-
| 8
| 152.4
| [[12/11]]
|-
| 9
| 171.4
| ''[[10/9]]'', [[11/10]], [[31/28]], [[32/29]]
|-
| 10
| 190.5
| [[19/17]], [[29/26]], [[39/35]], [[49/44]]
|-
| 11
| 209.5
| [[9/8]]
|-
| 12
| 228.6
| [[8/7]]
|-
| 13
| 247.6
| [[15/13]]
|-
| 14
| 266.7
| [[7/6]]
|-
| 15
| 285.7
| [[13/11]]
|-
| 16
| 304.8
| [[31/26]]
|-
| 17
| 323.8
| [[6/5]]
|-
| 18
| 342.9
| [[11/9]], [[28/23]], [[39/32]]
|-
| 19
| 361.9
| [[16/13]], [[26/21]], [[27/22]]
|-
| 20
| 381.0
| [[5/4]]
|-
| 21
| 400.0
| [[29/23]], [[44/35]], [[49/39]]
|-
| 22
| 419.0
| [[14/11]]
|-
| 23
| 438.1
| [[9/7]]
|-
| 24
| 457.1
| [[13/10]]
|-
| 25
| 476.2
| [[21/16]]
|-
| 26
| 495.2
| [[4/3]]
|-
| 27
| 514.3
| [[35/26]]
|-
| 28
| 533.3
| [[15/11]], ''[[27/20]]''
|-
| 29
| 552.4
| [[11/8]]
|-
| 30
| 571.4
| [[18/13]], [[32/23]]
|-
| 31
| 590.5
| [[7/5]]
|-
| 32
| 609.5
| [[10/7]]
|-
| 33
| 628.6
| [[13/9]], [[23/16]]
|-
| 34
| 647.6
| [[16/11]]
|-
| 35
| 666.7
| [[22/15]]
|-
| 36
| 685.7
| [[52/35]]
|-
| 37
| 704.8
| [[3/2]]
|-
| 38
| 723.8
| [[32/21]]
|-
| 39
| 742.9
| [[20/13]]
|-
| 40
| 761.9
| [[14/9]]
|-
| 41
| 781.0
| [[11/7]]
|-
| 42
| 800.0
| [[35/22]], [[46/29]]
|-
| 43
| 819.0
| [[8/5]]
|-
| 44
| 838.1
| [[13/8]], [[21/13]], [[44/27]]
|-
| 45
| 857.1
| [[18/11]], [[23/14]], [[64/39]]
|-
| 46
| 876.2
| [[5/3]]
|-
| 47
| 895.2
| [[52/31]]
|-
| 48
| 914.3
| [[22/13]]
|-
| 49
| 933.3
| [[12/7]]
|-
| 50
| 952.4
| [[26/15]]
|-
| 51
| 971.4
| [[7/4]]
|-
| 52
| 990.5
| [[16/9]]
|-
| 53
| 1009.5
| [[34/19]], [[52/29]], [[70/39]], [[88/49]]
|-
| 54
| 1028.6
| ''[[9/5]]'', [[20/11]], [[29/16]], [[56/31]]
|-
| 55
| 1047.6
| [[11/6]]
|-
| 56
| 1066.7
| [[13/7]], [[24/13]]
|-
| 57
| 1085.7
| [[15/8]], [[28/15]]
|-
| 58
| 1104.8
| ''[[40/21]]'', [[66/35]]
|-
| 59
| 1123.8
| [[21/11]], [[23/12]], [[25/13]], [[44/23]], ''[[52/27]]''
|-
| 60
| 1142.9
| [[27/14]], [[29/15]], [[31/16]], [[35/18]], ''[[48/25]]'', [[56/29]], [[60/31]], [[64/33]]
|-
| 61
| 1161.9
| [[45/23]], ''[[55/28]]'', [[88/45]], [[96/49]], ''[[160/81]]''
|-
| 62
| 1181.0
| ''[[49/25]]'', [[63/32]], [[65/33]], ''[[108/55]]'', [[180/91]], [[208/105]]
|-
| 63
| 1200.0
| [[2/1]]
|}
<nowiki>*</nowiki> As a 2.3.5.7.11.13.23.29.31-subgroup (no-17 no-19 31-limit) temperament, inconsistent intervals in ''italics''
 
See the below section for a machine-generated table including higher-limit ratios selected with a mind towards higher accuracy.
 
=== Higher-accuracy interpretations ===
 
The following table was created using [[User:Godtone#My python 3 code|Godtone's code]] with the command <code><nowiki>interpret_edo(63,ol=53,no=[5,17,19,25,27,37,41,51],add=[73,75,87,89,91,93,105],dec="''",wiki=23)</nowiki></code> (run in a Python 3 interactive console) plus manual correction of the order of some inconsistent intervals, removal of unsimplified intervals of 75, and adding of (the inconsistent but simple) 10/9, 21/20 and their octave-complements.
 
As the command and description indicates, it is a(n accurate) "no-5's"* no-17's no-19's no-25's no-27's no-37's no-41's 49-odd-limit add-53 add-63 add-73 add-87 add-89 add-91 add-93 add-105 interpretation, tuned to the strengths of 63edo. * Note that because of the cancellation of factors, some odd harmonics of 5 (the simpler/more relevant ones) are present, EG {{nowrap|75/3 {{=}} 25}}, {{nowrap|45/3 {{=}} 15}}, {{nowrap|105/75 {{=}} 7/5}}, {{nowrap| 75/35/2 {{=}} 15/14}}, and {{nowrap|45/9 {{=}} 5}}, so it isn't really "no-5's", just has a de-emphasized focus.
 
Intervals are listed in order of size, so that one can know their relative order at a glance and deem the value of the interpretation for a harmonic context, and [[23-limit]] intervals are highlighted for navigability as [[13-limit]] intervals are more likely to already have pages, and as we are excluding primes 17 and 19, we are only adding prime 23 to the 13-limit.
 
Inconsistent intervals are ''in italics''.
 
{| class="wikitable center-all right-2 left-3 mw-collapsible mw-collapsed"
|-
! Degree
! Cents
! Approximate ratios<ref group="note">{{sg|limit=2.3.5.7.11.13.23.29.31.43.47.53.73.89-subgroup (no-17's no-19's no-37's no-41's 53-limit add-73 add-89 add-105)}} Note that due to the error on 5, only low-complexity intervals involving 5 are included here.</ref>
|-
| 0
| 0.0
| [[1/1]]
|-
| 1
| 19.05
| 106/105, [[105/104]], 94/93, 93/92, [[92/91]], [[91/90]], 90/89, 89/88, 88/87, 87/86, 73/72, [[65/64]], [[64/63]]
|-
| 2
| 38.1
| ''[[66/65]]'', 53/52, [[49/48]], 48/47, 47/46, 93/91, [[46/45]], 91/89, [[45/44]], 89/87, 44/43, 43/42
|-
| 3
| 57.14
| [[36/35]], [[33/32]], 32/31, 94/91, 31/30, 92/89, [[91/88]], 30/29, 89/86, 29/28, ''[[25/24]]''
|-
| 4
| 76.19
| [[26/25]], 49/47, 73/70, [[24/23]], 47/45, 93/89, [[23/22]], 91/87, 45/43, [[22/21]]
|-
| 5
| 95.24
| ''[[21/20]]'', 98/93, [[96/91]], 94/89, 56/53, 93/88, 92/87, 91/86, 89/84, [[35/33]], [[52/49]]
|-
| 6
| 114.29
| 33/31, [[49/46]], [[16/15]], 47/44, 78/73, 31/29, 46/43, [[15/14]]
|-
| 7
| 133.33
| [[14/13]], 96/89, 94/87, 93/86, 53/49, [[13/12]]
|-
| 8
| 152.38
| [[49/45]], [[12/11]], 47/43, [[35/32]], 58/53, [[23/21]]
|-
| 9
| 171.43
| [[11/10]], 98/89, 43/39, 32/29, 53/48, 116/105, 73/66, 52/47, 31/28, ''[[10/9]]''
|-
| 10
| 190.48
| [[49/44]], [[39/35]], 29/26, 48/43, 105/94, 104/93, 47/42
|-
| 11
| 209.52
| ''[[28/25]]'', [[9/8]], 98/87, 53/47, [[44/39]], 35/31, [[26/23]], 60/53, ''[[25/22]]''
|-
| 12
| 228.57
| 33/29, 49/43, 106/93, 73/64, 89/78, [[105/92]], [[8/7]]
|-
| 13
| 247.62
| 84/73, 53/46, [[15/13]], [[52/45]]
|-
| 14
| 266.67
| ''29/25'', 36/31, 106/91, [[7/6]], 104/89, 62/53
|-
| 15
| 285.71
| 73/62, 53/45, 86/73, [[33/28]], [[46/39]], 105/89, 124/105, [[13/11]], 58/49
|-
| 16
| 304.76
| 106/89, 56/47, 87/73, 31/26, [[105/88]], 43/36, 104/87
|-
| 17
| 323.81
| [[6/5]], 112/93, 53/44, 47/39, 88/73, 35/29, 64/53, 29/24, 52/43
|-
| 18
| 342.86
| 73/60, [[28/23]], 106/87, [[39/32]], [[128/105]], 89/73, 105/86, [[11/9]], [[60/49]]
|-
| 19
| 361.9
| 43/35, [[16/13]], 53/43, 90/73, 58/47, 89/72, [[26/21]]
|-
| 20
| 380.95
| 31/25, 36/29, 87/70, [[56/45]], 66/53, 91/73, 116/93, [[5/4]]
|-
| 21
| 400.0
| [[49/39]], [[44/35]], 39/31, 112/89, 73/58, 92/73, 29/23, 53/42, [[91/72]], 62/49
|-
| 22
| 419.05
| [[33/26]], 89/70, [[14/11]], 93/73, 116/91, 60/47, [[23/18]]
|-
| 23
| 438.1
| ''[[32/25]]'', [[9/7]], 112/87, 94/73, 58/45, 40/31, 31/24
|-
| 24
| 457.14
| [[13/10]], 56/43, 43/33, 116/89, 73/56, [[30/23]], 47/36, [[64/49]]
|-
| 25
| 476.19
| [[21/16]], [[46/35]], 96/73, 29/22, [[120/91]], 62/47, 70/53
|-
| 26
| 495.24
| 93/70, [[4/3]]
|-
| 27
| 514.29
| 98/73, 47/35, 43/32, 39/29, [[35/26]], [[66/49]], 31/23, 120/89, 89/66, 58/43
|-
| 28
| 533.33
| 42/31, 72/53, 53/39, 87/64, [[49/36]], 64/47, 124/91, [[15/11]]
|-
| 29
| 552.38
| [[48/35]], [[11/8]], 128/93, 73/53, 62/45, [[91/66]], 40/29, 29/21
|-
| 30
| 571.43
| [[18/13]], 43/31, 146/105, 89/64, [[32/23]], [[39/28]], 124/89, [[46/33]], 60/43
|-
| 31
| 590.48
| [[7/5]], 87/62, 73/52, 66/47, [[45/32]], [[128/91]], 31/22
|-
| 32
| 609.52
| 44/31, [[91/64]], [[64/45]], 47/33, 104/73, 124/87, [[10/7]]
|-
| 33
| 628.57
| 43/30, [[33/23]], 89/62, [[56/39]], [[23/16]], 128/89, 105/73, 62/43, [[13/9]]
|-
| 34
| 647.62
| 42/29, 29/20, [[132/91]], 45/31, 106/73, 93/64, [[16/11]], [[35/24]]
|-
| 35
| 666.67
| [[22/15]], 91/62, 47/32, [[72/49]], 128/87, 78/53, 53/36, 31/21
|-
| 36
| 685.71
| 43/29, 132/89, 89/60, 46/31, [[49/33]], [[52/35]], 58/39, 64/43, 70/47, 73/49
|-
| 37
| 704.76
| [[3/2]], 140/93
|-
| 38
| 723.81
| 53/35, 47/31, [[91/60]], 44/29, 73/48, [[35/23]], [[32/21]]
|-
| 39
| 742.86
| [[49/32]], 72/47, [[23/15]], 112/73, 89/58, 66/43, 43/28, [[20/13]]
|-
| 40
| 761.9
| 48/31, 31/20, 45/29, 73/47, 87/56, [[14/9]], ''[[25/16]]''
|-
| 41
| 780.95
| [[36/23]], 47/30, 91/58, 146/93, [[11/7]], 140/89, [[52/33]]
|-
| 42
| 800.0
| 49/31, [[144/91]], 84/53, 46/29, 73/46, 116/73, 89/56, 62/39, [[35/22]], [[78/49]]
|-
| 43
| 819.05
| [[8/5]], 93/58, 146/91, 53/33, [[45/28]], 140/87, 29/18, 50/31
|-
| 44
| 838.1
| [[21/13]], 144/89, 47/29, 73/45, 86/53, [[13/8]], 70/43
|-
| 45
| 857.14
| [[49/30]], [[18/11]], 172/105, 146/89, [[105/64]], [[64/39]], 87/53, [[23/14]], 120/73
|-
| 46
| 876.19
| 43/26, 48/29, 53/32, 58/35, 73/44, 78/47, 88/53, 93/56, [[5/3]]
|-
| 47
| 895.24
| 87/52, 72/43, [[176/105]], 52/31, 146/87, 47/28, 89/53
|-
| 48
| 914.29
| 49/29, [[22/13]], 105/62, 178/105, [[39/23]], [[56/33]], 73/43, 90/53, 124/73
|-
| 49
| 933.33
| 53/31, 89/52, [[12/7]], 91/53, 31/18, ''50/29''
|-
| 50
| 952.38
| [[45/26]], [[26/15]], 92/53, 73/42
|-
| 51
| 971.43
| [[7/4]], [[184/105]], 156/89, 128/73, 93/53, 86/49, 58/33
|-
| 52
| 990.48
| ''[[44/25]]'', 53/30, [[23/13]], 62/35, [[39/22]], 94/53, 87/49, [[16/9]], ''[[25/14]]''
|-
| 53
| 1009.52
| 84/47, 93/52, 188/105, 43/24, 52/29, [[70/39]], [[88/49]]
|-
| 54
| 1028.57
| ''[[9/5]]', 56/31, 47/26, 132/73, 105/58, 96/53, 29/16, 78/43, 89/49, [[20/11]]
|-
| 55
| 1047.62
| [[42/23]], 53/29, [[64/35]], 86/47, [[11/6]], [[90/49]]
|-
| 56
| 1066.67
| [[24/13]], 98/53, 172/93, 87/47, 89/48, [[13/7]]
|-
| 57
| 1085.71
| [[28/15]], 43/23, 58/31, 73/39, 88/47, [[15/8]], [[92/49]], 62/33
|-
| 58
| 1104.76
| [[49/26]], [[66/35]], 168/89, 172/91, 87/46, 176/93, 53/28, 89/47, [[91/48]], 93/49, ''[[40/21]]''
|-
| 59
| 1123.81
| [[21/11]], 86/45, 174/91, [[44/23]], 178/93, 90/47, [[23/12]], 140/73, 94/49, [[25/13]]
|-
| 60
| 1142.86
| ''[[48/25]]'', 56/29, 172/89, 29/15, [[176/91]], 89/46, 60/31, 91/47, 31/16, [[64/33]], [[35/18]]
|-
| 61
| 1161.9
| 84/43, 43/22, 174/89, [[88/45]], 178/91, [[45/23]], 182/93, 92/47, 47/24, [[96/49]], 104/53
|-
| 62
| 1180.95
| [[63/32]], 144/73, 172/87, 87/44, 176/89, 89/45, [[180/91]], [[91/46]], 184/93, 93/47, [[208/105]], 105/53
|-
| 63
| 1200.0
| [[2/1]]
|}
<references group="note" />
 
== Notation ==
 
=== Ups and downs notation ===
 
63edo can be notated using [[ups and downs notation|ups and downs]]. Trup is equivalent to quudsharp, trudsharp is equivalent to quup, etc.
{{Sharpness-sharp7a}}
 
Alternatively, sharps and flats with arrows borrowed from [[Helmholtz–Ellis notation]] can be used:
{{Sharpness-sharp7}}
 
=== Sagittal notation ===
This notation uses the same sagittal sequence as [[56edo #Sagittal notation|56edo]].
 
==== Evo flavor ====
<imagemap>
File:63-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 639 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[64/63]]
rect 120 80 220 106 [[81/80]]
rect 220 80 340 106 [[33/32]]
default [[File:63-EDO_Evo_Sagittal.svg]]
</imagemap>
 
==== Revo flavor ====
<imagemap>
File:63-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 705 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[64/63]]
rect 120 80 220 106 [[81/80]]
rect 220 80 340 106 [[33/32]]
default [[File:63-EDO_Revo_Sagittal.svg]]
</imagemap>
 
== Approximation to JI ==
=== Interval mappings ===
{{Q-odd-limit intervals}}
 
=== Zeta peak index ===
{{ZPI
| zpi = 321
| steps = 63.0192885705350
| step size = 19.0417890652143
| tempered height = 6.768662
| pure height = 6.534208
| integral = 1.049023
| gap = 15.412920
| octave = 1199.63271110850
| consistent = 8
| distinct = 8
}}
 
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
! [[TE error|Absolute]] (¢)
! [[TE simple badness|Relative]] (%)
|-
| 2.3
| {{Monzo| 100 -63 }}
| {{Mapping| 63 100 }}
| -0.885
| 0.885
| 4.65
|-
| 2.3.5
| 3125/3072, 1638400/1594323
| {{Mapping| 63 100 146 }}
| +0.177
| 1.67
| 8.77
|-
| 2.3.5.7
| 225/224, 245/243, 51200/50421
| {{Mapping| 63 100 146 177 }}
| -0.099
| 1.52
| 8.00
|-
| 2.3.5.7.11
| 100/99, 225/224, 245/243, 1331/1323
| {{mapping| 63 100 146 177 218 }}
| -0.141
| 1.37
| 7.17
|-
| 2.3.5.7.11.13
| 100/99, 169/168, 225/224, 245/243, 275/273
| {{mapping| 63 100 146 177 218 233 }}
| -0.008
| 1.28
| 6.73
|}
 
=== Rank-2 temperaments ===
{| class="wikitable center-all left-5"
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator
|-
! Periods<br>per 8ve
! Generator*
! Cents*
! Associated<br>ratio*
! Temperament
|-
| 1
| 2\63
| 38.10
| 49/48
| [[Slender]]
|-
| 1
| 13\63
| 247.62
| 15/13
| [[Immune]]
|-
| 1
| 19\63
| 361.90
| 16/13
| [[Submajor]]
|-
| 1
| 20\63
| 380.95
| 5/4
| [[Magic]]
|-
| 1
| 25\63
| 476.19
| 21/16
| [[Subfourth]]
|-
| 3
| 26\63<br>(5\63)
| 495.24<br>(95.24)
| 4/3<br>(21/20)
| [[Fog]]
|-
| 7
| 26\63<br>(1\63)
| 495.24<br>(19.05)
| 4/3<br>(64/63)
| [[Sevond]]
|-
| 9
| 13\63<br>(1\63)
| 247.62<br>(19.05)
| 15/13<br>(99/98)
| [[Enneaportent]]
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[normal lists|minimal form]] in parentheses if distinct
 
== Scales ==
* Approximation of ''[[Pelog]] lima'': 6 9 21 6 21
* Timeywimey (original/default tuning): 16 10 7 4 11 5 10
* Sandcastle (original/default tuning): 8 10 8 11 8 8 10
 
== Instruments ==
* [[Lumatone mapping for 63edo]]
* [[Skip fretting system 63 3 17]]
 
== Music ==
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/IYLzF4ogl_w ''microtonal improvisation in 63edo''] (2025)
 
; [[Cam Taylor]]
* [https://soundcloud.com/cam-taylor-2-1/12tone63edo1 ''Improvisation in 12-tone fifths chain''] (2015)
* [https://soundcloud.com/cam-taylor-2-1/17-out-of-63edo-wurly-those-early-dreams ''those early dreams''] (2016)
* [https://archive.org/details/17_63EDOEarlyDreamsTwo ''early dreams 2''] (2016)
* [https://soundcloud.com/camtaylor-1/63edobosanquetaxis-8thjuly2016-237111323-seconds-and-otonal-shifts ''Seconds and Otonal Shifts''] (2016)
 
[[Category:Listen]]

Latest revision as of 08:08, 27 July 2025

← 62edo 63edo 64edo →
Prime factorization 32 × 7
Step size 19.0476 ¢ 
Fifth 37\63 (704.762 ¢)
Semitones (A1:m2) 7:4 (133.3 ¢ : 76.19 ¢)
Consistency limit 7
Distinct consistency limit 7

63 equal divisions of the octave (abbreviated 63edo or 63ed2), also called 63-tone equal temperament (63tet) or 63 equal temperament (63et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 63 equal parts of about 19 ¢ each. Each step represents a frequency ratio of 21/63, or the 63rd root of 2.

Theory

63edo is almost consistent to the 15-odd-limit; the only inconsistency is that 10/9 is mapped to 9\63 (1\7, the same as what 11/10 is mapped to consistently) so that it is almost 11 ¢ out of tune. This corresponds to 63edo exaggerating the syntonic comma, 81/80, to two steps, so that it finds a somewhat flat mean-tone between ~10/9 and ~9/8.

As an equal temperament, it tempers out 3125/3072 in the 5-limit and 225/224, 245/243, and 875/864 in the 7-limit, so that it supports magic temperament. In the 11-limit it tempers out 100/99, supporting 11-limit magic, plus 385/384 and 540/539, 896/891. In the 13-limit it tempers out 169/168, 275/273, 640/637, 352/351, 364/363 and 676/675. It provides the optimal patent val for immune, the 29 & 34d temperament in the 7-, 11- and 13-limit.

63 is also a fascinating division to look at in the 47-limit. Although it does not deal as well with primes 5, 17, 19, 37 and 41, it excels in the 2.3.7.11.13.23.29.31.43.47 subgroup, and is a great candidate for a gentle tuning. Its regular augmented fourth (+6 fifths) is less than 0.3 cents sharp of 23/16, therefore tempering out 736/729. Its diesis (+12 fifths) can represent 33/32, 32/31, 30/29, 29/28, 28/27, as well as 91/88, and more, so it is very versatile, making chains of fifths of 12 tones or longer very useful in covering harmonic and melodic ground while providing a lot of different colour in different keys. We can take advantage of the representation of 27:28:29:30:31:32:33, which splits 11/9 into six "small dieses" as a result; here it can be seen more clearly why these are not regular quarter-tones so are best distinguished from such with the qualifier "large", as otherwise we would expect to see some flavour of minor third after six of them.

A 17-tone fifths chain looks on the surface a little similar to 17edo, but as −17 fifths gets us to 64/63, observing the comma becomes an essential part in progressions favouring prime 7. Furthermore, its prime 5 is far from unusable; although 25/16 is barely inconsistent, this affords the tuning supporting 7-limit magic, which may be considered interesting or desirable in of itself. And if this was not enough, if you really want to, it offers reasonable approximations to some yet higher primes too; namely 43/32, 47/32, and 53/32; see the tables below.

Prime harmonics

Approximation of prime harmonics in 63edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31 37
Error Absolute (¢) +0.00 +2.81 -5.36 +2.60 +1.06 -2.43 +9.33 +7.25 +0.30 -1.01 -2.18 -3.72
Relative (%) +0.0 +14.7 -28.1 +13.7 +5.6 -12.8 +49.0 +38.1 +1.6 -5.3 -11.4 -19.6
Steps
(reduced) 		63
(0) 		100
(37) 		146
(20) 		177
(51) 		218
(29) 		233
(44) 		258
(6) 		268
(16) 		285
(33) 		306
(54) 		312
(60) 		328
(13)
Approximation of prime harmonics in 63edo (continued)
Harmonic 41 43 47 53 59 61 67 71 73 79 83 89
Error Absolute (¢) +9.03 +2.77 +1.16 +2.69 +7.50 +6.92 -3.12 -8.27 +0.78 -2.63 +7.10 +0.55
Relative (%) +47.4 +14.5 +6.1 +14.1 +39.3 +36.4 -16.4 -43.4 +4.1 -13.8 +37.3 +2.9
Steps
(reduced) 		338
(23) 		342
(27) 		350
(35) 		361
(46) 		371
(56) 		374
(59) 		382
(4) 		387
(9) 		390
(12) 		397
(19) 		402
(24) 		408
(30)

Subsets and supersets

Since 63 factors into primes as 32 × 7, 63edo has subset edos 3, 7, 9, and 21.

Its representation of the 2.3.5.7.13 subgroup (no-11's 13-limit) can uniquely be described in terms of accurate approximations contained in its main subsets of 7edo and 9edo:

If we avoid equating 14/13 and 13/12 (which is by far the highest damage equivalence) so that we achieve 7/6 = 2\9 directly, we get the 63 & 441 microtemperament in the same subgroup.

Intervals

Degree Cents Approximate ratios*
0 0.0 1/1
1 19.0 50/49, 55/54, 64/63, 65/64, 91/90, 105/104
2 38.1 45/44, 46/45, 49/48, 56/55, 66/65, 81/80
3 57.1 25/24, 28/27, 29/28, 30/29, 31/30, 32/31, 33/32, 36/35
4 76.2 22/21, 23/22, 24/23, 26/25, 27/26
5 95.2 21/20, 35/33
6 114.3 15/14, 16/15
7 133.3 13/12, 14/13
8 152.4 12/11
9 171.4 10/9, 11/10, 31/28, 32/29
10 190.5 19/17, 29/26, 39/35, 49/44
11 209.5 9/8
12 228.6 8/7
13 247.6 15/13
14 266.7 7/6
15 285.7 13/11
16 304.8 31/26
17 323.8 6/5
18 342.9 11/9, 28/23, 39/32
19 361.9 16/13, 26/21, 27/22
20 381.0 5/4
21 400.0 29/23, 44/35, 49/39
22 419.0 14/11
23 438.1 9/7
24 457.1 13/10
25 476.2 21/16
26 495.2 4/3
27 514.3 35/26
28 533.3 15/11, 27/20
29 552.4 11/8
30 571.4 18/13, 32/23
31 590.5 7/5
32 609.5 10/7
33 628.6 13/9, 23/16
34 647.6 16/11
35 666.7 22/15
36 685.7 52/35
37 704.8 3/2
38 723.8 32/21
39 742.9 20/13
40 761.9 14/9
41 781.0 11/7
42 800.0 35/22, 46/29
43 819.0 8/5
44 838.1 13/8, 21/13, 44/27
45 857.1 18/11, 23/14, 64/39
46 876.2 5/3
47 895.2 52/31
48 914.3 22/13
49 933.3 12/7
50 952.4 26/15
51 971.4 7/4
52 990.5 16/9
53 1009.5 34/19, 52/29, 70/39, 88/49
54 1028.6 9/5, 20/11, 29/16, 56/31
55 1047.6 11/6
56 1066.7 13/7, 24/13
57 1085.7 15/8, 28/15
58 1104.8 40/21, 66/35
59 1123.8 21/11, 23/12, 25/13, 44/23, 52/27
60 1142.9 27/14, 29/15, 31/16, 35/18, 48/25, 56/29, 60/31, 64/33
61 1161.9 45/23, 55/28, 88/45, 96/49, 160/81
62 1181.0 49/25, 63/32, 65/33, 108/55, 180/91, 208/105
63 1200.0 2/1

* As a 2.3.5.7.11.13.23.29.31-subgroup (no-17 no-19 31-limit) temperament, inconsistent intervals in italics

See the below section for a machine-generated table including higher-limit ratios selected with a mind towards higher accuracy.

Higher-accuracy interpretations

The following table was created using Godtone's code with the command interpret_edo(63,ol=53,no=[5,17,19,25,27,37,41,51],add=[73,75,87,89,91,93,105],dec="''",wiki=23) (run in a Python 3 interactive console) plus manual correction of the order of some inconsistent intervals, removal of unsimplified intervals of 75, and adding of (the inconsistent but simple) 10/9, 21/20 and their octave-complements.

As the command and description indicates, it is a(n accurate) "no-5's"* no-17's no-19's no-25's no-27's no-37's no-41's 49-odd-limit add-53 add-63 add-73 add-87 add-89 add-91 add-93 add-105 interpretation, tuned to the strengths of 63edo. * Note that because of the cancellation of factors, some odd harmonics of 5 (the simpler/more relevant ones) are present, EG 75/3 = 25, 45/3 = 15, 105/75 = 7/5, 75/35/2 = 15/14, and 45/9 = 5, so it isn't really "no-5's", just has a de-emphasized focus.

Intervals are listed in order of size, so that one can know their relative order at a glance and deem the value of the interpretation for a harmonic context, and 23-limit intervals are highlighted for navigability as 13-limit intervals are more likely to already have pages, and as we are excluding primes 17 and 19, we are only adding prime 23 to the 13-limit.

Inconsistent intervals are in italics.

Degree Cents Approximate ratios[note 1]
0 0.0 1/1
1 19.05 106/105, 105/104, 94/93, 93/92, 92/91, 91/90, 90/89, 89/88, 88/87, 87/86, 73/72, 65/64, 64/63
2 38.1 66/65, 53/52, 49/48, 48/47, 47/46, 93/91, 46/45, 91/89, 45/44, 89/87, 44/43, 43/42
3 57.14 36/35, 33/32, 32/31, 94/91, 31/30, 92/89, 91/88, 30/29, 89/86, 29/28, 25/24
4 76.19 26/25, 49/47, 73/70, 24/23, 47/45, 93/89, 23/22, 91/87, 45/43, 22/21
5 95.24 21/20, 98/93, 96/91, 94/89, 56/53, 93/88, 92/87, 91/86, 89/84, 35/33, 52/49
6 114.29 33/31, 49/46, 16/15, 47/44, 78/73, 31/29, 46/43, 15/14
7 133.33 14/13, 96/89, 94/87, 93/86, 53/49, 13/12
8 152.38 49/45, 12/11, 47/43, 35/32, 58/53, 23/21
9 171.43 11/10, 98/89, 43/39, 32/29, 53/48, 116/105, 73/66, 52/47, 31/28, 10/9
10 190.48 49/44, 39/35, 29/26, 48/43, 105/94, 104/93, 47/42
11 209.52 28/25, 9/8, 98/87, 53/47, 44/39, 35/31, 26/23, 60/53, 25/22
12 228.57 33/29, 49/43, 106/93, 73/64, 89/78, 105/92, 8/7
13 247.62 84/73, 53/46, 15/13, 52/45
14 266.67 29/25, 36/31, 106/91, 7/6, 104/89, 62/53
15 285.71 73/62, 53/45, 86/73, 33/28, 46/39, 105/89, 124/105, 13/11, 58/49
16 304.76 106/89, 56/47, 87/73, 31/26, 105/88, 43/36, 104/87
17 323.81 6/5, 112/93, 53/44, 47/39, 88/73, 35/29, 64/53, 29/24, 52/43
18 342.86 73/60, 28/23, 106/87, 39/32, 128/105, 89/73, 105/86, 11/9, 60/49
19 361.9 43/35, 16/13, 53/43, 90/73, 58/47, 89/72, 26/21
20 380.95 31/25, 36/29, 87/70, 56/45, 66/53, 91/73, 116/93, 5/4
21 400.0 49/39, 44/35, 39/31, 112/89, 73/58, 92/73, 29/23, 53/42, 91/72, 62/49
22 419.05 33/26, 89/70, 14/11, 93/73, 116/91, 60/47, 23/18
23 438.1 32/25, 9/7, 112/87, 94/73, 58/45, 40/31, 31/24
24 457.14 13/10, 56/43, 43/33, 116/89, 73/56, 30/23, 47/36, 64/49
25 476.19 21/16, 46/35, 96/73, 29/22, 120/91, 62/47, 70/53
26 495.24 93/70, 4/3
27 514.29 98/73, 47/35, 43/32, 39/29, 35/26, 66/49, 31/23, 120/89, 89/66, 58/43
28 533.33 42/31, 72/53, 53/39, 87/64, 49/36, 64/47, 124/91, 15/11
29 552.38 48/35, 11/8, 128/93, 73/53, 62/45, 91/66, 40/29, 29/21
30 571.43 18/13, 43/31, 146/105, 89/64, 32/23, 39/28, 124/89, 46/33, 60/43
31 590.48 7/5, 87/62, 73/52, 66/47, 45/32, 128/91, 31/22
32 609.52 44/31, 91/64, 64/45, 47/33, 104/73, 124/87, 10/7
33 628.57 43/30, 33/23, 89/62, 56/39, 23/16, 128/89, 105/73, 62/43, 13/9
34 647.62 42/29, 29/20, 132/91, 45/31, 106/73, 93/64, 16/11, 35/24
35 666.67 22/15, 91/62, 47/32, 72/49, 128/87, 78/53, 53/36, 31/21
36 685.71 43/29, 132/89, 89/60, 46/31, 49/33, 52/35, 58/39, 64/43, 70/47, 73/49
37 704.76 3/2, 140/93
38 723.81 53/35, 47/31, 91/60, 44/29, 73/48, 35/23, 32/21
39 742.86 49/32, 72/47, 23/15, 112/73, 89/58, 66/43, 43/28, 20/13
40 761.9 48/31, 31/20, 45/29, 73/47, 87/56, 14/9, 25/16
41 780.95 36/23, 47/30, 91/58, 146/93, 11/7, 140/89, 52/33
42 800.0 49/31, 144/91, 84/53, 46/29, 73/46, 116/73, 89/56, 62/39, 35/22, 78/49
43 819.05 8/5, 93/58, 146/91, 53/33, 45/28, 140/87, 29/18, 50/31
44 838.1 21/13, 144/89, 47/29, 73/45, 86/53, 13/8, 70/43
45 857.14 49/30, 18/11, 172/105, 146/89, 105/64, 64/39, 87/53, 23/14, 120/73
46 876.19 43/26, 48/29, 53/32, 58/35, 73/44, 78/47, 88/53, 93/56, 5/3
47 895.24 87/52, 72/43, 176/105, 52/31, 146/87, 47/28, 89/53
48 914.29 49/29, 22/13, 105/62, 178/105, 39/23, 56/33, 73/43, 90/53, 124/73
49 933.33 53/31, 89/52, 12/7, 91/53, 31/18, 50/29
50 952.38 45/26, 26/15, 92/53, 73/42
51 971.43 7/4, 184/105, 156/89, 128/73, 93/53, 86/49, 58/33
52 990.48 44/25, 53/30, 23/13, 62/35, 39/22, 94/53, 87/49, 16/9, 25/14
53 1009.52 84/47, 93/52, 188/105, 43/24, 52/29, 70/39, 88/49
54 1028.57 9/5', 56/31, 47/26, 132/73, 105/58, 96/53, 29/16, 78/43, 89/49, 20/11
55 1047.62 42/23, 53/29, 64/35, 86/47, 11/6, 90/49
56 1066.67 24/13, 98/53, 172/93, 87/47, 89/48, 13/7
57 1085.71 28/15, 43/23, 58/31, 73/39, 88/47, 15/8, 92/49, 62/33
58 1104.76 49/26, 66/35, 168/89, 172/91, 87/46, 176/93, 53/28, 89/47, 91/48, 93/49, 40/21
59 1123.81 21/11, 86/45, 174/91, 44/23, 178/93, 90/47, 23/12, 140/73, 94/49, 25/13
60 1142.86 48/25, 56/29, 172/89, 29/15, 176/91, 89/46, 60/31, 91/47, 31/16, 64/33, 35/18
61 1161.9 84/43, 43/22, 174/89, 88/45, 178/91, 45/23, 182/93, 92/47, 47/24, 96/49, 104/53
62 1180.95 63/32, 144/73, 172/87, 87/44, 176/89, 89/45, 180/91, 91/46, 184/93, 93/47, 208/105, 105/53
63 1200.0 2/1
  1. ↑ Based on treating 63edo as a 2.3.5.7.11.13.23.29.31.43.47.53.73.89-subgroup (no-17's no-19's no-37's no-41's 53-limit add-73 add-89 add-105) temperament; other approaches are also possible. Note that due to the error on 5, only low-complexity intervals involving 5 are included here.

Notation

Ups and downs notation

63edo can be notated using ups and downs. Trup is equivalent to quudsharp, trudsharp is equivalent to quup, etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol                
                 
Flat symbol              
                 

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 56edo.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Approximation to JI

Interval mappings

The following tables show how 15-odd-limit intervals are represented in 63edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 63edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
15/13, 26/15 0.122 0.6
7/6, 12/7 0.204 1.1
11/8, 16/11 1.063 5.6
11/7, 14/11 1.540 8.1
11/6, 12/11 1.744 9.2
13/8, 16/13 2.432 12.8
15/8, 16/15 2.554 13.4
7/4, 8/7 2.603 13.7
3/2, 4/3 2.807 14.7
13/10, 20/13 2.929 15.4
9/7, 14/9 3.011 15.8
13/11, 22/13 3.495 18.4
15/11, 22/15 3.617 19.0
11/9, 18/11 4.551 23.9
13/7, 14/13 5.035 26.4
15/14, 28/15 5.157 27.1
13/12, 24/13 5.239 27.5
5/4, 8/5 5.361 28.1
9/8, 16/9 5.614 29.5
11/10, 20/11 6.424 33.7
7/5, 10/7 7.964 41.8
13/9, 18/13 8.046 42.2
9/5, 10/9 8.072 42.4
5/3, 6/5 8.168 42.9
15-odd-limit intervals in 63edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
15/13, 26/15 0.122 0.6
7/6, 12/7 0.204 1.1
11/8, 16/11 1.063 5.6
11/7, 14/11 1.540 8.1
11/6, 12/11 1.744 9.2
13/8, 16/13 2.432 12.8
15/8, 16/15 2.554 13.4
7/4, 8/7 2.603 13.7
3/2, 4/3 2.807 14.7
13/10, 20/13 2.929 15.4
9/7, 14/9 3.011 15.8
13/11, 22/13 3.495 18.4
15/11, 22/15 3.617 19.0
11/9, 18/11 4.551 23.9
13/7, 14/13 5.035 26.4
15/14, 28/15 5.157 27.1
13/12, 24/13 5.239 27.5
5/4, 8/5 5.361 28.1
9/8, 16/9 5.614 29.5
11/10, 20/11 6.424 33.7
7/5, 10/7 7.964 41.8
13/9, 18/13 8.046 42.2
5/3, 6/5 8.168 42.9
9/5, 10/9 10.975 57.6

Zeta peak index

Tuning Strength Octave (cents) Integer limit
ZPI Steps
per 8ve 		Step size
(cents) 		Height Integral Gap Size Stretch Consistent Distinct
Tempered Pure
321zpi 63.019289 19.041789 6.768662 6.534208 1.049023 15.41292 1199.632711 −0.367289 8 8

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [100 -63⟩ [⟨63 100]] -0.885 0.885 4.65
2.3.5 3125/3072, 1638400/1594323 [⟨63 100 146]] +0.177 1.67 8.77
2.3.5.7 225/224, 245/243, 51200/50421 [⟨63 100 146 177]] -0.099 1.52 8.00
2.3.5.7.11 100/99, 225/224, 245/243, 1331/1323 [⟨63 100 146 177 218]] -0.141 1.37 7.17
2.3.5.7.11.13 100/99, 169/168, 225/224, 245/243, 275/273 [⟨63 100 146 177 218 233]] -0.008 1.28 6.73

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 2\63 38.10 49/48 Slender
1 13\63 247.62 15/13 Immune
1 19\63 361.90 16/13 Submajor
1 20\63 380.95 5/4 Magic
1 25\63 476.19 21/16 Subfourth
3 26\63
(5\63) 		495.24
(95.24) 		4/3
(21/20) 		Fog
7 26\63
(1\63) 		495.24
(19.05) 		4/3
(64/63) 		Sevond
9 13\63
(1\63) 		247.62
(19.05) 		15/13
(99/98) 		Enneaportent

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

  • Approximation of Pelog lima: 6 9 21 6 21
  • Timeywimey (original/default tuning): 16 10 7 4 11 5 10
  • Sandcastle (original/default tuning): 8 10 8 11 8 8 10

Instruments

Music

Bryan Deister
Cam Taylor
Retrieved from "https://en.xen.wiki/index.php?title=63edo&oldid=205159"