Hemifamity family: Difference between revisions
m Cleanup; recategory |
m Text replacement - "Category:Temperament families" to "Category:Temperament families Category:Pages with mostly numerical content" |
||
| (31 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
The '''hemifamity family''' of | {{Technical data page}} | ||
The '''hemifamity family''' of [[rank-3 temperament|rank-3]] [[regular temperament|temperaments]] [[tempering out|tempers out]] [[5120/5103]] ({{monzo|legend=1| 10 -6 1 -1 }}), the hemifamity comma. These temperaments divide an exact or approximate septimal quartertone, [[36/35]] into two equal steps, each representing [[81/80]]~[[64/63]], the syntonic comma or the septimal comma. Therefore, classical and septimal intervals are found by the same [[chain of fifths]] inflected by the same comma to the opposite sides. In addition we may identify [[10/7]] by the augmented fourth (C–F#) and [[50/49]] by the [[Pythagorean comma]]. Hemifamity can be compared to [[garibaldi]], with garibaldi expanding the interpretations of 81/80~64/63 to include the Pythagorean comma (collapsing to a rank-2 structure), or alternatively, hemifamity can be seen as liberating the syntonic-septimal comma from garibaldi's chain of fifths. | |||
It is therefore very handy to adopt an additional module of accidentals such as arrows to represent the syntonic~septimal comma, in which case we have [[5/4]] at the down major third (C–vE) and [[7/4]] at the down minor seventh (C–vBb). | |||
[[ | |||
== Hemifamity == | |||
[[Subgroup]]: 2.3.5.7 | |||
[ | [[Comma list]]: [[5120/5103]] | ||
{{Mapping|legend=1| 1 0 0 10 | 0 1 0 -6 | 0 0 1 1 }} | |||
: mapping generators: ~2, ~3, ~5 | |||
[| | [[Mapping to lattice]]: [{{val| 0 1 2 -4 }}, {{val| 0 0 1 1 }}] | ||
|0 0 1 | |||
Lattice basis: | |||
: 3/2 length = 0.5670, 10/9 length = 1.8063 | |||
: Angle (3/2, 10/9) = 82.112 degrees | |||
[[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 702.7918, ~5/4 = 386.0144 | |||
[[Minimax tuning]]: c = 5120/5103 | |||
* [[7-odd-limit]]: 3 and 7 1/7c sharp, 5 just | |||
: {{monzo list| 1 0 0 0 | 10/7 1/7 1/7 -1/7 | 0 0 1 0 | 10/7 -6/7 1/7 6/7 }} | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.5.7/3 | |||
* [[9-odd-limit]]: 3 1/8c sharp, 5 just, 7 1/4c sharp | |||
: {{monzo list| 1 0 0 0 | 5/4 1/4 1/8 -1/8 | 0 0 1 0 | 5/2 -3/2 1/4 3/4 }} | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.5.9/7 | |||
{{Optimal ET sequence|legend=1| 41, 53, 87, 94, 99, 239, 251, 292, 391, 881bd, 1272bcdd }} | |||
[[Badness]] (Smith): 0.153 × 10<sup>-3</sup> | |||
[[Projection pair]]s: 7 5120/729 | |||
; Music | |||
* [http://www.archive.org/details/Choraled ''Choraled''] [http://www.archive.org/download/Choraled/Genewardsmith-Choraled.mp3 play] by [[Gene Ward Smith]] | |||
* [http://clones.soonlabel.com/public/micro/hemifamity27/hemifamity27-IF-20100917.mp3 ''Hemifamity27''] by [[Chris Vaisvil]] | |||
=== Overview to extensions === | |||
==== 11- and 13-limit extensions ==== | |||
Strong extensions of hemifamity are [[#Pele|pele]], [[#Laka|laka]], [[#Akea|akea]], and [[#Lono|lono]]. The rest are weak extensions. Using the arrow to represent the syntonic~septimal comma, pele finds the [[11/8]] at the down diminished fifth (C–vGb); laka, up augmented third (C–^E#); akea, double-up fourth (C–^^F); lono, triple-down augmented fourth (C–v<sup>3</sup>F#). All these extensions follow the trend of tuning the fifth a little sharp. Thus a successful mapping of 13 can be found by fixing the [[13/11]] at the minor third (C–Eb), tempering out [[352/351]], [[847/845]], and [[2080/2079]]. | |||
==== Subgroup extensions ==== | |||
A notable 2.3.5.7.19 subgroup extension, counterpyth, is given right below. | |||
=== Counterpyth === | |||
{{Main| Counterpyth }} | |||
Developed analogous to [[parapyth]], counterpyth is an extension of hemifamity with an even milder fifth, as it finds [[19/15]] at the major third (C–E) and [[19/10]] at the major seventh (C–B). Notice the factorization {{nowrap| 5120/5103 {{=}} ([[400/399]])⋅([[1216/1215]]) }}. Other important ratios are [[21/19]] at the diminished third (C–Ebb) and [[19/14]] at the augmented third (C–E#). | |||
It can be further extended via the mappings of laka or akea, while working less well with pele or lono due to their much sharper fifths. | |||
Subgroup: 2.3.5.7.19 | |||
Comma list: 400/399, 1216/1215 | |||
Mapping: {{mapping| 1 0 0 10 -6 | 0 1 0 -6 5 | 0 0 1 1 1 }} | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.6411, ~5/4 = 385.4452 | |||
{{Optimal ET sequence|legend=0| 12, 29, 41, 53, 94, 99, 140, 152, 292h, 444dh }} | |||
Badness (Smith): 0.212 × 10<sup>-3</sup> | |||
== Pele == | |||
{{Main| Pele }} | |||
{{See also| Pentacircle clan }} | |||
[[Subgroup]]: 2.3.5.7.11 | |||
[[Comma list]]: 441/440, 896/891 | |||
{{Mapping|legend=1| 1 0 0 10 17 | 0 1 0 -6 -10 | 0 0 1 1 1 }} | |||
[[Mapping to lattice]]: [{{val| 0 1 4 -2 -6 }}, {{val| 0 0 -1 -1 -1 }}] | |||
[[ | Lattice basis: | ||
: 3/2 length = 0.3812, 56/55 length = 1.5893 | |||
: Angle(3/2, 56/55) = 90.4578 degrees | |||
[[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 703.2829, ~5/4 = 386.5647 | |||
[[Minimax tuning]]: | |||
* [[11-odd-limit]] | |||
: [{{monzo| 1 0 0 0 0 }}, {{monzo| 17/10 0 1/10 0 -1/10 }}, {{monzo| 17/5 -2 6/5 0 -1/5 }}, {{monzo| 16/5 -2 3/5 0 2/5 }}, {{monzo| 17/5 -2 1/5 0 4/5 }}] | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.9/5.11/9 | |||
{{Optimal ET sequence|legend=1| 29, 41, 58, 87, 99e, 145, 186e }} | |||
[[Badness]] (Smith): 0.648 × 10<sup>-3</sup> | |||
[[Projection pair]]s: 7 5120/729 11 655360/59049 | |||
= | === 13-limit === | ||
Subgroup: 2.3.5.7.11.13 | |||
Comma list: 196/195, 352/351, 364/363 | |||
Mapping: {{mapping| 1 0 0 10 17 22 | 0 1 0 -6 -10 -13 | 0 0 1 1 1 1 }} | |||
| | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 703.4398, ~5/4 = 386.8933 | |||
Minimax tuning: | |||
* 13-odd-limit unchanged-interval (eigenmonzo) basis: 2.9/5.13/9 | |||
* 15-odd-limit unchanged-interval (eigenmonzo) basis: 2.5/3.13/9 | |||
{{Optimal ET sequence|legend=0| 29, 41, 46, 58, 87, 145, 232 }} | |||
Badness (Smith): 0.703 × 10<sup>-3</sup> | |||
=== 17-limit === | |||
Subgroup: 2.3.5.7.11.13.17 | |||
Comma list: 196/195, 256/255, 352/351, 364/363 | |||
Mapping: {{mapping| 1 0 0 10 17 22 8 | 0 1 0 -6 -10 -13 -1 | 0 0 1 1 1 1 -1 }} | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 703.5544, ~5/4 = 387.9654 | |||
{{Optimal ET sequence|legend=0| 29, 41, 46, 58, 87, 99ef, 145 }} | |||
Badness (Smith): 0.930 × 10<sup>-3</sup> | |||
== Laka == | |||
{{Main| Laka }} | |||
Laka can be described as the {{nowrap| 41 & 53 & 58 }} temperament, tempering out [[540/539]]. [[Gene Ward Smith]] considered it to be a [[17-limit]] temperament, assigning †442/441 ({{nowrap| 41g & 53 & 58 }}) as the main extension. It should be noted that {{nowrap| 41 & 53g & 58 }} also makes for a possible extension. | |||
<blockquote> | |||
It's the way the numbers fall. The Laka geometry happens to work reasonably well in the 13-limit but not so well in the 17-limit. There isn't one obvious 17-limit extension and none of them are competitive with other 17-limit temperaments. | |||
</blockquote> | |||
—[[Graham Breed]]<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_101682.html#101776 Yahoo! Tuning Group | ''Laka 17-limit minimax planar temperament'']</ref> | |||
It makes most sense as a 2.3.5.7.11.13.19-[[subgroup]] temperament, omitting harmonic 17, as the 19 is accurate and easily available in a 24-tone scale. | |||
[[Subgroup]]: 2.3.5.7.11 | |||
[[Comma list]]: 540/539, 5120/5103 | |||
{{Mapping|legend=1| 1 0 0 10 -18 | 0 1 0 -6 15 | 0 0 1 1 -1 }} | |||
[[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 702.5133, ~5/4 = 385.5563 | |||
[[ | |||
[[Minimax tuning]] | [[Minimax tuning]] | ||
* [[11-odd-limit]] | |||
: [{{monzo| 1 0 0 0 0 }}, {{monzo| 4/3 0 2/21 -1/21 1/21 }}, {{monzo| 0 0 1 0 0 }}, {{monzo| 2 0 3/7 2/7 -2/7 }}, {{monzo| 2 0 3/7 -5/7 5/7 }}] | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.5.11/7 | |||
{{Optimal ET sequence|legend=1| 41, 53, 58, 94, 99e, 152, 497de, 555dee, 707ddee, 859bddee }} | |||
[[Badness]] (Smith): 0.825 × 10<sup>-3</sup> | |||
[[Projection pair]]s: 5120/729 11 14348907/1310720 | |||
=== 13-limit === | |||
Subgroup: 2.3.5.7.11.13 | |||
Comma list: 352/351, 540/539, 729/728 | |||
Mapping: {{mapping| 1 0 0 10 -18 -13 | 0 1 0 -6 15 12 | 0 0 1 1 -1 -1 }} | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.4078, ~5/4 = 385.5405 | |||
Minimax tuning: | |||
* 13- and 15-odd-limit | |||
: [{{monzo| 1 0 0 0 0 0 }}, {{monzo| 13/8 -1/2 1/8 0 0 1/8 }}, {{monzo| 13/4 -3 5/4 0 0 1/4 }}, {{monzo| 7/2 0 1/2 0 0 -1/2 }}, {{monzo| 25/8 -9/2 5/8 0 0 13/8 }}, {{monzo| 13/4 -3 1/4 0 0 5/4 }}] | |||
: unchanged-interval (eigenmonzo) basis: 2.11.13/7 | |||
{{Optimal ET sequence|legend=0| 41, 53, 58, 94, 111, 152f, 415dff }}* | |||
<nowiki>*</nowiki> optimal patent val: [[205edo|205]] | |||
Badness (Smith): 0.822 × 10<sup>-3</sup> | |||
=== 2.3.5.7.11.13.19 subgroup === | |||
Subgroup: 2.3.5.7.11.13.19 | |||
Comma list: 352/351, 400/399, 456/455, 495/494 | |||
Mapping: {{mapping| 1 0 0 10 -18 -13 -6 | 0 1 0 -6 15 12 5 | 0 0 1 1 -1 -1 1 }} | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.4062, ~5/4 = 385.5254 | |||
{{Optimal ET sequence|legend=0| 41, 53, 58h, 94, 111, 152f, 415dffhh }}* | |||
<nowiki>*</nowiki> optimal patent val: [[205edo|205]] | |||
Badness (Smith): 0.661 × 10<sup>-3</sup> | |||
=== 17-limit === | |||
Subgroup: 2.3.5.7.11.13.17 | |||
Comma list: 352/351, 442/441, 540/539, 561/560 | |||
Mapping: {{mapping| 1 0 0 10 -18 -13 32 | 0 1 0 -6 15 12 -22 | 0 0 1 1 -1 -1 3 }} | |||
Minimax tuning: | |||
* 17-odd-limit | |||
: [{{monzo| 1 0 0 0 0 0 0 }}, {{monzo| 13/12 0 0 1/12 1/6 -1/12 0 }}, {{monzo| -7/4 0 0 5/4 3/2 -5/4 0 }}, {{monzo| 7/4 0 0 3/4 1/2 -3/4 0 }}, {{monzo| 0 0 0 0 1 0 0 }}, {{monzo| 7/4 0 0 -1/4 1/2 1/4 0 }}, {{monzo| 35/12 0 0 23/12 5/6 -23/12 0 }}] | |||
: unchanged-interval (eigenmonzo) basis: 2.11.13/7 | |||
= | {{Optimal ET sequence|legend=0| 58, 94, 111, 152f, 205, 263df }} | ||
Badness (Smith): 1.19 × 10<sup>-3</sup> | |||
[| | == Akea == | ||
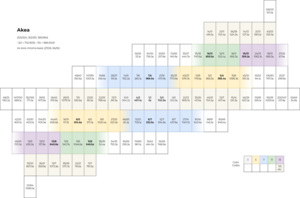
| | [[File:Lattice Akea.png|thumb|Lattice for 13-limit akea.]] | ||
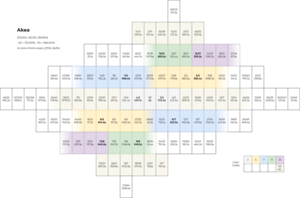
[[File:Lattice Akea-commatic.png|thumb|Ditto, but rearranged to basis {~2, ~3, ~81/80}.]] | |||
[[ | [[Subgroup]]: 2.3.5.7.11 | ||
[[Comma list]]: 385/384, 2200/2187 | |||
[[Comma]] | |||
{{Mapping|legend=1| 1 0 0 10 -3 | 0 1 0 -6 7 | 0 0 1 1 -2 }} | |||
[ | [[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 702.8909, ~5/4 = 385.3273 | ||
[[ | [[Minimax tuning]]: | ||
* [[11-odd-limit]] | |||
: [{{monzo| 1 0 0 0 0 }}, {{monzo| 5/3 0 1/6 -1/6 0 }}, {{monzo| 26/9 0 13/18 -7/18 -1/3 }}, {{monzo| 26/9 0 -5/18 11/18 -1/3 }}, {{monzo| 26/9 0 -5/18 -7/18 2/3 }}] | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.7/5.11/5 | |||
{{Optimal ET sequence|legend=1| 34, 41, 53, 87, 140, 181, 321 }} | |||
[[Badness]] (Smith): 0.998 × 10<sup>-3</sup> | |||
=== 13-limit === | |||
Subgroup: 2.3.5.7.11.13 | |||
Comma list: 325/324, 352/351, 385/384 | |||
Mapping: {{mapping| 1 0 0 10 -3 2 | 0 1 0 -6 7 4 | 0 0 1 1 -2 -2 }} | |||
[ | Lattice basis: | ||
: 3/2 length = 0.5354, 27/20 length = 1.0463 | |||
: Angle (3/2, 27/20) = 80.5628 degrees | |||
Mapping to lattice: [{{val| 0 1 3 -3 1 -2 }}, {{val| 0 0 -1 -1 2 2 }}] | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.9018, ~5/4 = 385.4158 | |||
[|1 0 0 0 0 | Minimax tuning: | ||
|26/9 0 13/18 -7/18 -1/3 | * 13- and 15-odd-limit | ||
|26/9 0 -5/18 11/18 -1/3 | : [{{monzo| 1 0 0 0 0 0 }}, {{monzo| 5/3 0 1/6 -1/6 0 0 }}, {{monzo| 26/9 0 13/18 -7/18 -1/3 0 }}, {{monzo| 26/9 0 -5/18 11/18 -1/3 0 }}, {{monzo| 26/9 0 -5/18 -7/18 2/3 0 }}, {{monzo| 26/9 0 -7/9 1/9 2/3 0 }}] | ||
|26/9 0 -5/18 -7/18 2/3 | : unchanged-interval (eigenmonzo) basis: 2.7/5.11/5 | ||
{{Optimal ET sequence|legend=0| 34, 41, 46, 53, 87, 140, 321, 461e }} | |||
Badness (Smith): 0.822 × 10<sup>-3</sup> | |||
[[ | Scales: [[akea46_13]] | ||
== Lono == | |||
[[Subgroup]]: 2.3.5.7.11 | |||
[[Comma list]]: 176/175, 5120/5103 | |||
= | {{Mapping|legend=1| 1 0 0 10 6 | 0 1 0 -6 -6 | 0 0 1 1 3 }} | ||
[[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 702.8941, ~5/4 = 388.5932 | |||
{{Optimal ET sequence|legend=1| 46, 53, 58, 99, 111, 268cd }} | |||
[[Badness]] (Smith): 1.18 × 10<sup>-3</sup> | |||
=== 13-limit === | |||
Subgroup: 2.3.5.7.11.13 | |||
Comma list: 176/175, 351/350, 847/845 | |||
Mapping: {{mapping| 1 0 0 10 6 11 | 0 1 0 -6 -6 -9 | 0 0 1 1 3 3 }} | |||
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.8670, ~5/4 = 388.6277 | |||
{{Optimal ET sequence|legend=0| 46, 53, 58, 99, 104c, 111, 268cd }} | |||
Badness (Smith): 0.908 × 10<sup>-3</sup> | |||
== Kapo == | |||
[[Subgroup]]: 2.3.5.7.11 | |||
[[Comma list]]: 3025/3024, 5120/5103 | |||
= | {{Mapping|legend=1| 1 0 0 10 7 | 0 1 1 -5 -2 | 0 0 2 2 -1 }} | ||
: mapping generators: ~2, ~3, ~128/99 | |||
[ | [[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~3/2 = 702.8776, ~128/99 = 441.7516 | ||
[[ | [[Minimax tuning]]: | ||
* [[11-odd-limit]]: | |||
: [{{monzo| 1 0 0 0 0 }}, {{monzo| 8/5 2/5 0 -1/15 -2/15 }}, {{monzo| 14/5 6/5 0 7/15 -16/15 }}, {{monzo| 16/5 -6/5 0 13/15 -4/15 }}, {{monzo| 16/5 -6/5 0 -2/15 11/15 }}] | |||
: [[Eigenmonzo basis|unchanged-interval (eigenmonzo) basis]]: 2.9/7.11/9 | |||
{{Optimal ET sequence|legend=1| 41, 87, 111, 152, 239, 391 }} | |||
[[ | [[Badness]] (Smith): 0.994 × 10<sup>-3</sup> | ||
[[ | == Namaka == | ||
[[Subgroup]]: 2.3.5.7.11 | |||
[[Comma list]]: 3388/3375, 5120/5103 | |||
= | {{Mapping|legend=1| 1 0 0 10 -6 | 0 2 0 -12 9 | 0 0 1 1 1 }} | ||
: mapping generators: ~2, ~400/231, ~5 | |||
[[Optimal tuning]] ([[CTE]]): ~2 = 1200.0000, ~400/231 = 951.4956, ~5/4 = 386.7868 | |||
{{Optimal ET sequence|legend=1| 29, 53, 58, 87, 111, 140, 198 }} | |||
[[Badness]] (Smith): 1.74 × 10<sup>-3</sup> | |||
=== 13-limit === | |||
Subgroup: 2.3.5.7.11.13 | |||
Comma list: 352/351, 676/675, 847/845 | |||
Mapping: {{mapping| 1 0 0 10 -6 -1 | 0 2 0 -12 9 3 | 0 0 1 1 1 1 }} | |||
= | Optimal tuning (CTE): ~2 = 1200.0000, ~26/15 = 951.4871, ~5/4 = 386.6606 | ||
{{Optimal ET sequence|legend=0| 29, 53, 58, 87, 111, 140, 198 }} | |||
Badness (Smith): 0.781 × 10<sup>-3</sup> | |||
== Notes == | |||
[[Category: | [[Category:Temperament families]] | ||
[[Category: | [[Category:Pages with mostly numerical content]] | ||
[[Category:Hemifamity]] | [[Category:Hemifamity family| ]] <!-- main article --> | ||
[[Category:Hemifamity| ]] <!-- key article --> | |||
[[Category:Rank 3]] | [[Category:Rank 3]] | ||
[[Category:Listen]] | |||
Latest revision as of 00:41, 24 June 2025
- This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.
The hemifamity family of rank-3 temperaments tempers out 5120/5103 (monzo: [10 -6 1 -1⟩), the hemifamity comma. These temperaments divide an exact or approximate septimal quartertone, 36/35 into two equal steps, each representing 81/80~64/63, the syntonic comma or the septimal comma. Therefore, classical and septimal intervals are found by the same chain of fifths inflected by the same comma to the opposite sides. In addition we may identify 10/7 by the augmented fourth (C–F#) and 50/49 by the Pythagorean comma. Hemifamity can be compared to garibaldi, with garibaldi expanding the interpretations of 81/80~64/63 to include the Pythagorean comma (collapsing to a rank-2 structure), or alternatively, hemifamity can be seen as liberating the syntonic-septimal comma from garibaldi's chain of fifths.
It is therefore very handy to adopt an additional module of accidentals such as arrows to represent the syntonic~septimal comma, in which case we have 5/4 at the down major third (C–vE) and 7/4 at the down minor seventh (C–vBb).
Hemifamity
Subgroup: 2.3.5.7
Mapping: [⟨1 0 0 10], ⟨0 1 0 -6], ⟨0 0 1 1]]
- mapping generators: ~2, ~3, ~5
Mapping to lattice: [⟨0 1 2 -4], ⟨0 0 1 1]]
Lattice basis:
- 3/2 length = 0.5670, 10/9 length = 1.8063
- Angle (3/2, 10/9) = 82.112 degrees
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.7918, ~5/4 = 386.0144
Minimax tuning: c = 5120/5103
- 7-odd-limit: 3 and 7 1/7c sharp, 5 just
- [[1 0 0 0⟩, [10/7 1/7 1/7 -1/7⟩, [0 0 1 0⟩, [10/7 -6/7 1/7 6/7⟩]
- unchanged-interval (eigenmonzo) basis: 2.5.7/3
- 9-odd-limit: 3 1/8c sharp, 5 just, 7 1/4c sharp
- [[1 0 0 0⟩, [5/4 1/4 1/8 -1/8⟩, [0 0 1 0⟩, [5/2 -3/2 1/4 3/4⟩]
- unchanged-interval (eigenmonzo) basis: 2.5.9/7
Optimal ET sequence: 41, 53, 87, 94, 99, 239, 251, 292, 391, 881bd, 1272bcdd
Badness (Smith): 0.153 × 10-3
Projection pairs: 7 5120/729
- Music
Overview to extensions
11- and 13-limit extensions
Strong extensions of hemifamity are pele, laka, akea, and lono. The rest are weak extensions. Using the arrow to represent the syntonic~septimal comma, pele finds the 11/8 at the down diminished fifth (C–vGb); laka, up augmented third (C–^E#); akea, double-up fourth (C–^^F); lono, triple-down augmented fourth (C–v3F#). All these extensions follow the trend of tuning the fifth a little sharp. Thus a successful mapping of 13 can be found by fixing the 13/11 at the minor third (C–Eb), tempering out 352/351, 847/845, and 2080/2079.
Subgroup extensions
A notable 2.3.5.7.19 subgroup extension, counterpyth, is given right below.
Counterpyth
Developed analogous to parapyth, counterpyth is an extension of hemifamity with an even milder fifth, as it finds 19/15 at the major third (C–E) and 19/10 at the major seventh (C–B). Notice the factorization 5120/5103 = (400/399)⋅(1216/1215). Other important ratios are 21/19 at the diminished third (C–Ebb) and 19/14 at the augmented third (C–E#).
It can be further extended via the mappings of laka or akea, while working less well with pele or lono due to their much sharper fifths.
Subgroup: 2.3.5.7.19
Comma list: 400/399, 1216/1215
Mapping: [⟨1 0 0 10 -6], ⟨0 1 0 -6 5], ⟨0 0 1 1 1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.6411, ~5/4 = 385.4452
Optimal ET sequence: 12, 29, 41, 53, 94, 99, 140, 152, 292h, 444dh
Badness (Smith): 0.212 × 10-3
Pele
Subgroup: 2.3.5.7.11
Comma list: 441/440, 896/891
Mapping: [⟨1 0 0 10 17], ⟨0 1 0 -6 -10], ⟨0 0 1 1 1]]
Mapping to lattice: [⟨0 1 4 -2 -6], ⟨0 0 -1 -1 -1]]
Lattice basis:
- 3/2 length = 0.3812, 56/55 length = 1.5893
- Angle(3/2, 56/55) = 90.4578 degrees
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 703.2829, ~5/4 = 386.5647
- [[1 0 0 0 0⟩, [17/10 0 1/10 0 -1/10⟩, [17/5 -2 6/5 0 -1/5⟩, [16/5 -2 3/5 0 2/5⟩, [17/5 -2 1/5 0 4/5⟩]
- unchanged-interval (eigenmonzo) basis: 2.9/5.11/9
Optimal ET sequence: 29, 41, 58, 87, 99e, 145, 186e
Badness (Smith): 0.648 × 10-3
Projection pairs: 7 5120/729 11 655360/59049
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 196/195, 352/351, 364/363
Mapping: [⟨1 0 0 10 17 22], ⟨0 1 0 -6 -10 -13], ⟨0 0 1 1 1 1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 703.4398, ~5/4 = 386.8933
Minimax tuning:
- 13-odd-limit unchanged-interval (eigenmonzo) basis: 2.9/5.13/9
- 15-odd-limit unchanged-interval (eigenmonzo) basis: 2.5/3.13/9
Optimal ET sequence: 29, 41, 46, 58, 87, 145, 232
Badness (Smith): 0.703 × 10-3
17-limit
Subgroup: 2.3.5.7.11.13.17
Comma list: 196/195, 256/255, 352/351, 364/363
Mapping: [⟨1 0 0 10 17 22 8], ⟨0 1 0 -6 -10 -13 -1], ⟨0 0 1 1 1 1 -1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 703.5544, ~5/4 = 387.9654
Optimal ET sequence: 29, 41, 46, 58, 87, 99ef, 145
Badness (Smith): 0.930 × 10-3
Laka
Laka can be described as the 41 & 53 & 58 temperament, tempering out 540/539. Gene Ward Smith considered it to be a 17-limit temperament, assigning †442/441 (41g & 53 & 58) as the main extension. It should be noted that 41 & 53g & 58 also makes for a possible extension.
It's the way the numbers fall. The Laka geometry happens to work reasonably well in the 13-limit but not so well in the 17-limit. There isn't one obvious 17-limit extension and none of them are competitive with other 17-limit temperaments.
It makes most sense as a 2.3.5.7.11.13.19-subgroup temperament, omitting harmonic 17, as the 19 is accurate and easily available in a 24-tone scale.
Subgroup: 2.3.5.7.11
Comma list: 540/539, 5120/5103
Mapping: [⟨1 0 0 10 -18], ⟨0 1 0 -6 15], ⟨0 0 1 1 -1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.5133, ~5/4 = 385.5563
- [[1 0 0 0 0⟩, [4/3 0 2/21 -1/21 1/21⟩, [0 0 1 0 0⟩, [2 0 3/7 2/7 -2/7⟩, [2 0 3/7 -5/7 5/7⟩]
- unchanged-interval (eigenmonzo) basis: 2.5.11/7
Optimal ET sequence: 41, 53, 58, 94, 99e, 152, 497de, 555dee, 707ddee, 859bddee
Badness (Smith): 0.825 × 10-3
Projection pairs: 5120/729 11 14348907/1310720
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 352/351, 540/539, 729/728
Mapping: [⟨1 0 0 10 -18 -13], ⟨0 1 0 -6 15 12], ⟨0 0 1 1 -1 -1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.4078, ~5/4 = 385.5405
Minimax tuning:
- 13- and 15-odd-limit
- [[1 0 0 0 0 0⟩, [13/8 -1/2 1/8 0 0 1/8⟩, [13/4 -3 5/4 0 0 1/4⟩, [7/2 0 1/2 0 0 -1/2⟩, [25/8 -9/2 5/8 0 0 13/8⟩, [13/4 -3 1/4 0 0 5/4⟩]
- unchanged-interval (eigenmonzo) basis: 2.11.13/7
Optimal ET sequence: 41, 53, 58, 94, 111, 152f, 415dff*
* optimal patent val: 205
Badness (Smith): 0.822 × 10-3
2.3.5.7.11.13.19 subgroup
Subgroup: 2.3.5.7.11.13.19
Comma list: 352/351, 400/399, 456/455, 495/494
Mapping: [⟨1 0 0 10 -18 -13 -6], ⟨0 1 0 -6 15 12 5], ⟨0 0 1 1 -1 -1 1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.4062, ~5/4 = 385.5254
Optimal ET sequence: 41, 53, 58h, 94, 111, 152f, 415dffhh*
* optimal patent val: 205
Badness (Smith): 0.661 × 10-3
17-limit
Subgroup: 2.3.5.7.11.13.17
Comma list: 352/351, 442/441, 540/539, 561/560
Mapping: [⟨1 0 0 10 -18 -13 32], ⟨0 1 0 -6 15 12 -22], ⟨0 0 1 1 -1 -1 3]]
Minimax tuning:
- 17-odd-limit
- [[1 0 0 0 0 0 0⟩, [13/12 0 0 1/12 1/6 -1/12 0⟩, [-7/4 0 0 5/4 3/2 -5/4 0⟩, [7/4 0 0 3/4 1/2 -3/4 0⟩, [0 0 0 0 1 0 0⟩, [7/4 0 0 -1/4 1/2 1/4 0⟩, [35/12 0 0 23/12 5/6 -23/12 0⟩]
- unchanged-interval (eigenmonzo) basis: 2.11.13/7
Optimal ET sequence: 58, 94, 111, 152f, 205, 263df
Badness (Smith): 1.19 × 10-3
Akea
Subgroup: 2.3.5.7.11
Comma list: 385/384, 2200/2187
Mapping: [⟨1 0 0 10 -3], ⟨0 1 0 -6 7], ⟨0 0 1 1 -2]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.8909, ~5/4 = 385.3273
- [[1 0 0 0 0⟩, [5/3 0 1/6 -1/6 0⟩, [26/9 0 13/18 -7/18 -1/3⟩, [26/9 0 -5/18 11/18 -1/3⟩, [26/9 0 -5/18 -7/18 2/3⟩]
- unchanged-interval (eigenmonzo) basis: 2.7/5.11/5
Optimal ET sequence: 34, 41, 53, 87, 140, 181, 321
Badness (Smith): 0.998 × 10-3
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 325/324, 352/351, 385/384
Mapping: [⟨1 0 0 10 -3 2], ⟨0 1 0 -6 7 4], ⟨0 0 1 1 -2 -2]]
Lattice basis:
- 3/2 length = 0.5354, 27/20 length = 1.0463
- Angle (3/2, 27/20) = 80.5628 degrees
Mapping to lattice: [⟨0 1 3 -3 1 -2], ⟨0 0 -1 -1 2 2]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.9018, ~5/4 = 385.4158
Minimax tuning:
- 13- and 15-odd-limit
- [[1 0 0 0 0 0⟩, [5/3 0 1/6 -1/6 0 0⟩, [26/9 0 13/18 -7/18 -1/3 0⟩, [26/9 0 -5/18 11/18 -1/3 0⟩, [26/9 0 -5/18 -7/18 2/3 0⟩, [26/9 0 -7/9 1/9 2/3 0⟩]
- unchanged-interval (eigenmonzo) basis: 2.7/5.11/5
Optimal ET sequence: 34, 41, 46, 53, 87, 140, 321, 461e
Badness (Smith): 0.822 × 10-3
Scales: akea46_13
Lono
Subgroup: 2.3.5.7.11
Comma list: 176/175, 5120/5103
Mapping: [⟨1 0 0 10 6], ⟨0 1 0 -6 -6], ⟨0 0 1 1 3]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.8941, ~5/4 = 388.5932
Optimal ET sequence: 46, 53, 58, 99, 111, 268cd
Badness (Smith): 1.18 × 10-3
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 176/175, 351/350, 847/845
Mapping: [⟨1 0 0 10 6 11], ⟨0 1 0 -6 -6 -9], ⟨0 0 1 1 3 3]]
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.8670, ~5/4 = 388.6277
Optimal ET sequence: 46, 53, 58, 99, 104c, 111, 268cd
Badness (Smith): 0.908 × 10-3
Kapo
Subgroup: 2.3.5.7.11
Comma list: 3025/3024, 5120/5103
Mapping: [⟨1 0 0 10 7], ⟨0 1 1 -5 -2], ⟨0 0 2 2 -1]]
- mapping generators: ~2, ~3, ~128/99
Optimal tuning (CTE): ~2 = 1200.0000, ~3/2 = 702.8776, ~128/99 = 441.7516
- [[1 0 0 0 0⟩, [8/5 2/5 0 -1/15 -2/15⟩, [14/5 6/5 0 7/15 -16/15⟩, [16/5 -6/5 0 13/15 -4/15⟩, [16/5 -6/5 0 -2/15 11/15⟩]
- unchanged-interval (eigenmonzo) basis: 2.9/7.11/9
Optimal ET sequence: 41, 87, 111, 152, 239, 391
Badness (Smith): 0.994 × 10-3
Namaka
Subgroup: 2.3.5.7.11
Comma list: 3388/3375, 5120/5103
Mapping: [⟨1 0 0 10 -6], ⟨0 2 0 -12 9], ⟨0 0 1 1 1]]
- mapping generators: ~2, ~400/231, ~5
Optimal tuning (CTE): ~2 = 1200.0000, ~400/231 = 951.4956, ~5/4 = 386.7868
Optimal ET sequence: 29, 53, 58, 87, 111, 140, 198
Badness (Smith): 1.74 × 10-3
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 352/351, 676/675, 847/845
Mapping: [⟨1 0 0 10 -6 -1], ⟨0 2 0 -12 9 3], ⟨0 0 1 1 1 1]]
Optimal tuning (CTE): ~2 = 1200.0000, ~26/15 = 951.4871, ~5/4 = 386.6606
Optimal ET sequence: 29, 53, 58, 87, 111, 140, 198
Badness (Smith): 0.781 × 10-3