User:Sintel/Zeta working page

From Xenharmonic Wiki
Jump to navigation Jump to search
English Wikipedia has an article on:

The Riemann zeta function is an important function in number theory, most famous for its connection to the unsolved Riemann hypothesis. Beyond its mathematical significance, however, the zeta function has a surprising connection to music theory: it provides a quantitative measure of how effectively a given equal temperament approximates just intonation, relative to its size.

The zeta function provides a way to measure how well different equal-step tunings (including EDOs) approximate the infinite harmonic series. Unlike other evaluation methods that must select a specific prime limit as a cutoff, the zeta function approach incorporates all harmonics into its calculations, effectively functioning as an "infinite limit" measurement; and being a continuous function, the zeta function also is able to highlight nonoctave and tempered-octave tunings. However, zeta invariably prioritizes lower primes over higher primes (though in a "minimal" way provided the requirement of converging in the infinite limit) and therefore fails to capture systems with efficacy in certain subgroups.

If you look for a filter to quickly sort all the equal temperaments into those that approximate JI well and those that do not, the zeta peak EDOs below can be useful. The caveat is that it collapses the variety of characteristics of a temperament to a one-dimensional rating, with little capacity to show the nuances of each system. It is therefore best to keep in mind that judging the temperaments by zeta is no replacement for investigating each temperament in detail.

There are other metrics besides zeta for other definitions of "approximating well", such as the various optimised regular temperament tunings when applied to rank-1 (i.e. equal) temperaments. The zeta function approach presented here was developed primarily through the work of Gene Ward Smith, with additional contributions from Mike Battaglia.

Zeta peak EDOs

These lists give equal divisions of the octave that are better than any before them according to the zeta metric.

Zeta peak integer EDOs (pure octaves): 1, 2, 3, 5, 7, 10, 12, 19, 22, 31, 41, 53, 87, 118, 130, 171, 224, 270, 311, ...

Zeta peak EDOs (tempered octaves): 1, 2, 3, 4, 5, 7, 10, 12, 19, 22, 27, 31, 41, 53, 72, 99, 118, 130, 152, 171, 217, 224, 270, ...

See the section below for more information.

Intuitive explanation

When we talk about how well an equal temperament (ET) approximates just intonation, we're essentially asking: "How accurately can this system represent the harmonic series?"

These harmonics occur at whole-number ratios (1:1, 2:1, 3:1, 4:1, 5:1, etc.), which are not equally spaced. In contrast, equal temperaments divide the octave into equal steps, which is convenient but introduces slight deviations from these ratios. The zeta function essentially measures these deviations across the entire harmonic series, and gives more weight to lower harmonics, which are typically more audible and musically significant than higher ones.

For each harmonic in the series, we check how closely our equal temperament can approximate it. When a harmonic falls nearly exactly on an ET step, it receives a positive score. When it falls halfway between steps (requiring significant compromises in tuning), it receives a negative score. Lower harmonics (which make up simple intervals like the perfect fifth or major third) count more toward the final score than higher harmonics.

We then sum these weighted scores across the entire harmonic series. The resulting value tells us how well a given equal temperament approximates the harmonic series. A higher score indicates that many important harmonics are well-represented by the system. Remarkably, this final scoring function (given certain mathematical choices) turns out to be equivalent to the famous Riemann zeta function.

Derivation

Our goal is to derive a function that quantifies how effectively an equal division of the octave (EDO) approximates just intonation (JI). We will use the variable x to denote an EDO where x=12 represents 12edo. Importantly, we allow x to take continuous values, enabling it to represent any equal-step tuning where the step size is 1200/x cents. For example, x=8.202 corresponds to 13 equal divisions of the tritave.

To assess how well an equal temperament approximates the harmonic series, we need a function that measures the accuracy of approximation for each overtone.

The frequency ratio of the nth harmonic is n:1. In any equal temperament, to reach a ratio of n:1, we need [math]\displaystyle{ \log_2(n) }[/math] octaves, which is [math]\displaystyle{ x \log_2(n) }[/math] steps. If [math]\displaystyle{ x \log_2(n) }[/math] is very close to an integer, it means our equal temperament system can closely approximate that harmonic. If it's far from an integer, the approximation will be poor.

To quantify this proximity to integers, we can use the cosine function [math]\displaystyle{ f(x) = \cos(2 \pi x) }[/math], which peaks at integer values. This provides a simple metric for the relative error, where values close to 1 indicate good approximations and values close to -1 indicate poor ones.

Let's begin by considering only the first few harmonics and look at [math]\displaystyle{ f(x \log_2 2) }[/math], [math]\displaystyle{ f(x \log_2 3) }[/math], [math]\displaystyle{ f(x \log_2 4) }[/math], [math]\displaystyle{ f(x \log_2 5) }[/math].

The sum of these values gives us an overall quality measure:

[math]\displaystyle{ \sum_{n=1}^5 f(x \log_2 n) }[/math]
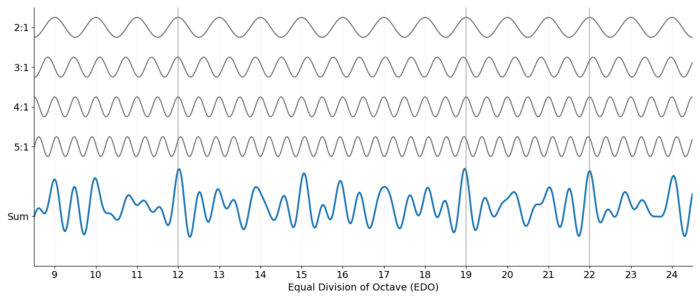
Plot of the cosine error function for the first 5 harmonics. Note how the peaks line up for some popular EDOs.

Ideally, we would like to extend this function to sum over the entire harmonic series:

[math]\displaystyle{ \sum_{n=1}^{\infty} f(x \log_2 n) }[/math]

However, this infinite sum does not converge. To address this issue, we can introduce a weighting factor that diminishes the contribution of higher harmonics:

[math]\displaystyle{ \begin{aligned} F(x) &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} f(x \log_2 n) \\ &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} \cos(2 \pi x \log_2 n) \end{aligned} }[/math]

This series converges provided that [math]\displaystyle{ \sigma \gt 1 }[/math], with the parameter sigma controlling how quickly the influence of higher harmonics declines.

We can reformulate this expression using Euler's formula [math]\displaystyle{ e^{ix} = \cos x + i \sin x }[/math], and replace the cosine with the real part of a complex exponential:

[math]\displaystyle{ \begin{aligned} F(x) &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} \mathrm{Re} \left( e^{-2 \pi i x \log_2 n} \right) \\ &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} e^{-2 \pi i x \log_2 n} \end{aligned} }[/math]

Using properties of logarithms, we know that [math]\displaystyle{ e^{x \log_2 n} = n^{\frac{x}{\ln 2}} }[/math], which gives us:

[math]\displaystyle{ \begin{aligned} F(x) &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} n^{-\frac{2 \pi}{\ln 2} i x} \\ \end{aligned} }[/math]

To clean this up a bit we will make a substitution and set [math]\displaystyle{ t = \tfrac{2 \pi}{\ln 2} x }[/math].

[math]\displaystyle{ \begin{aligned} F(x) &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} n^{-i t} \\ &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^{\sigma + i t}} \end{aligned} }[/math]

This final expression is precisely the definition of the Riemann zeta function [math]\displaystyle{ \zeta(s) }[/math] evaluated at the complex value [math]\displaystyle{ s = \sigma + i t = \sigma + \tfrac{2 \pi i}{\ln(2)} x }[/math]. Thus, our measure of tuning quality can be expressed directly in terms of this fundamental mathematical function:

[math]\displaystyle{ F(x) = \mathrm{Re} \, \zeta \left( \sigma + \frac{2 \pi i}{\ln(2)} x \right) }[/math]
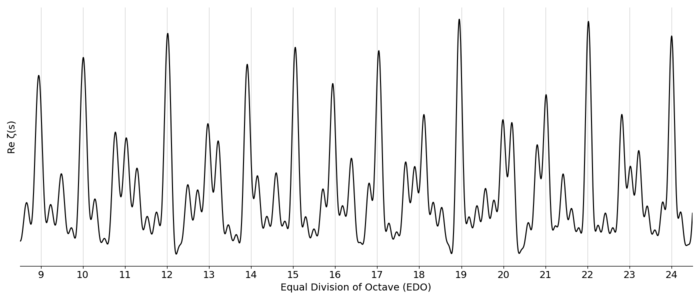
Real part of zeta function for sigma = 1.

Choice of sigma

Todo:

This section is incomplete! Discuss symmetry and add some conclusion

The infinite sum derived above converges only when [math]\displaystyle{ \mathrm{Re}(s) = \sigma \gt 1 }[/math]. However, mathematicians found that the zeta function can be "extended" or "continued" to other values of s where the original sum doesn't converge. This mathematical technique is called analytic continuation.

The extended zeta function is defined everywhere in the complex plane except at s = 1 (where there is a pole). This continuation allows us to evaluate the zeta function at values like [math]\displaystyle{ s = 1/2 + it }[/math], which lies on what's called the "critical line." When we use the zeta function to evaluate equal temperaments, we're interested in how well these temperaments approximate the harmonic series. The question becomes: which weight (value of s) gives us the most musically relevant information?

When s > 1, lower harmonics (especially the octave) dominate the evaluation. When s approaches 0, higher harmonics dominate. Neither extreme provides a balanced assessment of how well a temperament approximates the full harmonic series.

Zeta lists

Todo:

add the original lists back here, and discuss their relevance.

Optimal octave stretch

Another use for the Riemann zeta function is to determine the optimal tuning for an edo, meaning the optimal octave stretch. This is because the zeta peaks are typically not integers. The fractional part can give us the degree to which the generator diverges from what you would need to have the octave be a perfect 1200 ¢.

For all edos 1 through 100, and for a list of successively higher zeta peaks, taken to five decimal places, see table of zeta-stretched edos.

These octave-stretched edos are not the only tunings which can be produced from zeta peaks. They are only one type of tuning within a larger family of equal-step tunings called zeta peak indices. They have their own article here, with a table of the first 500 or so: zeta peak index (ZPI).

Removing primes

An Euler product formula for the Riemann zeta function can be easily derived:

[math]\displaystyle{ \displaystyle \zeta(s) = \prod_p \left(1 - p^{-s}\right)^{-1} }[/math]

where the product is over all primes p. Like the original sum, this product converges for values [math]\displaystyle{ \mathrm{Re}(s) = \sigma \gt 1 }[/math]. We can remove a finite list of primes from consideration by multiplying [math]\displaystyle{ \zeta(s) }[/math] by the corresponding factors [math]\displaystyle{ (1 - p^{-s}) }[/math] for each prime p we wish to remove. After doing this, the smallest prime remaining will dominate peak values for s. In particular if we remove the prime 2, [math]\displaystyle{ \left(1 - 2^{-s}\right)\zeta(s) }[/math] is now dominated by 3, and the large peak values occur near equal divisions of the tritave (3/1).

Along any line of constant [math]\displaystyle{ \sigma }[/math], it can be shown that:

[math]\displaystyle{ \displaystyle \left| 1 - p^{-\sigma - it} \right| = \sqrt{1 + \frac{1}{p^{2\sigma}} - \frac{2 \cos(t \ln p)}{p^\sigma}} }[/math];

in particular, on the critical line,

[math]\displaystyle{ \displaystyle \left| 1 - p^{-\frac{1}{2} - it} \right| = \sqrt{1 + \frac{1}{p} - \frac{2 \cos(t \ln p)}{\sqrt{p}}} }[/math].

Multiplying the Z-function by this factor of adjustment gives a Z-function with the prime p removed from consideration. Zeta peak and zeta integral tunings may then be found as before. Note that multiplying this factor is technically only accurate for sums whose result is related to the Z function rather than the real part of the zeta function.

For example, if we want to find zeta peak EDTs (division of the 3rd harmonic, or "tritave")—noting that here we must substitute [math]\displaystyle{ t = \frac{2\pi x}{\ln(3)} }[/math] instead of [math]\displaystyle{ \frac{2\pi x}{\ln(2)} }[/math]—in the no-twos subgroup, our modified zeta function is:

[math]\displaystyle{ \displaystyle \zeta \left( \sigma + \frac{2 \pi i}{\ln(3)}x \right) \sqrt{ \frac{3}{2} - \sqrt{2} \cos \left( \frac{2\pi\ln(2)}{\ln(3)} x \right) } }[/math].

Removing 2 leads to increasing adjusted peak values corresponding to EDTs into 4, 7, 9, 13, 15, 17, 26, 32, 39, 56, 69, 75, 88, 131, 245, 316,… parts. We can also compare zeta peak EDTs with pure and tempered tritaves just like zeta peak edos. A striking feature of this list is the appearance not only of 13edt, the Bohlen–Pierce division of the tritave, but the multiples 26 and 39 also.

Open problems

  • Are there metrics similar to zeta metrics, but for an EDO's performance at approximating arbitrary delta-rational chords?

Further information

For the interested reader, more information and derivations can be found in the appendix.

Links

Retrieved from "https://en.xen.wiki/index.php?title=User:Sintel/Zeta_working_page&oldid=192156"