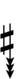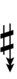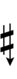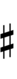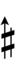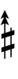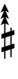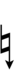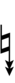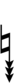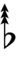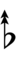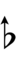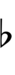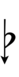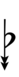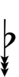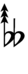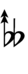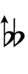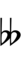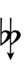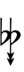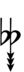63edo: Difference between revisions
m →Subsets and supersets: link to temp |
manually remove intervals of 75 as always being too damaged for their complexity, as evidenced by always appearing at the extreme ends of the spectrum of interpretations, if not as the most extreme entry then as the second-most, next to a vastly simpler interval that can justify the damage |
||
| Line 22: | Line 22: | ||
== Intervals == | == Intervals == | ||
The following table was created using [[User:Godtone#My python 3 code|Godtone's code]] with the command <code><nowiki>interpret_edo(63,ol=53,no=[5,17,19,25,27,37,41,51],add=[73,75,87,89,91,93,105],dec="''",wiki=23)</nowiki></code> (run in a Python 3 interactive console) plus manual correction of the order of some inconsistent intervals. | The following table was created using [[User:Godtone#My python 3 code|Godtone's code]] with the command <code><nowiki>interpret_edo(63,ol=53,no=[5,17,19,25,27,37,41,51],add=[73,75,87,89,91,93,105],dec="''",wiki=23)</nowiki></code> (run in a Python 3 interactive console) plus manual correction of the order of some inconsistent intervals and removal of unsimplified intervals of 75. | ||
As the command indicates, it is a(n accurate) no-5's* no-17's no-19's no-25's no-27's no-37's no-41's 49-odd-limit add-53 add-63 add-73 | As the command and description indicates, it is a(n accurate) "no-5's"* no-17's no-19's no-25's no-27's no-37's no-41's 49-odd-limit add-53 add-63 add-73 add-87 add-89 add-91 add-93 add-105 interpretation, tuned to the strengths of [[63edo]]. * Note that because of the cancellation of factors, some odd harmonics of 5 (the simpler/more relevant ones) are present, EG {{nowrap|75/3 {{=}} 25}}, {{nowrap|45/3 {{=}} 15}}, {{nowrap|105/75 {{=}} 7/5}}, {{nowrap| 75/35/2 {{=}} 15/14}}, and {{nowrap|45/9 {{=}} 5}}, so it isn't really "no-5's", just has a de-emphasized focus. | ||
Intervals are listed in order of size, so that one can know their relative order at a glance and deem the value of the interpretation for a harmonic context, and [[23-limit]] intervals are highlighted for navigability as [[13-limit]] intervals are more likely to already have pages, and as we are excluding primes 17 and 19, we are only adding prime 23 to the 13-limit. | Intervals are listed in order of size, so that one can know their relative order at a glance and deem the value of the interpretation for a harmonic context, and [[23-limit]] intervals are highlighted for navigability as [[13-limit]] intervals are more likely to already have pages, and as we are excluding primes 17 and 19, we are only adding prime 23 to the 13-limit. | ||
| Line 46: | Line 46: | ||
| 2 | | 2 | ||
| 38.1 | | 38.1 | ||
| ''[[66/65]]'', 53/52, [[49/48]], 48/47, 47/46, 93/91, [[46/45]], 91/89, [[45/44]], 89/87, 44/43, 43/42 | | ''[[66/65]]'', 53/52, [[49/48]], 48/47, 47/46, 93/91, [[46/45]], 91/89, [[45/44]], 89/87, 44/43, 43/42 | ||
|- | |- | ||
| 3 | | 3 | ||
| Line 90: | Line 90: | ||
| 13 | | 13 | ||
| 247.62 | | 247.62 | ||
| | | 84/73, 53/46, [[15/13]], [[52/45]] | ||
|- | |- | ||
| 14 | | 14 | ||
| 266.67 | | 266.67 | ||
| ''29/25'', 36/31, 106/91, [[7/6]], 104/89, 62/53 | | ''29/25'', 36/31, 106/91, [[7/6]], 104/89, 62/53 | ||
|- | |- | ||
| 15 | | 15 | ||
| 285.71 | | 285.71 | ||
| | | 73/62, 53/45, 86/73, [[33/28]], [[46/39]], 105/89, 124/105, [[13/11]], 58/49 | ||
|- | |- | ||
| 16 | | 16 | ||
| 304.76 | | 304.76 | ||
| | | 106/89, 56/47, 87/73, 31/26, [[105/88]], 43/36, 104/87 | ||
|- | |- | ||
| 17 | | 17 | ||
| 323.81 | | 323.81 | ||
| [[6/5]], 112/93, 53/44, 47/39, 88/73, 35/29, 64/53, 29/24, 52/43 | | [[6/5]], 112/93, 53/44, 47/39, 88/73, 35/29, 64/53, 29/24, 52/43 | ||
|- | |- | ||
| 18 | | 18 | ||
| 342.86 | | 342.86 | ||
| | | 73/60, [[28/23]], 106/87, [[39/32]], [[128/105]], 89/73, 105/86, [[11/9]], [[60/49]] | ||
|- | |- | ||
| 19 | | 19 | ||
| 361.9 | | 361.9 | ||
| | | 43/35, [[16/13]], 53/43, 90/73, 58/47, 89/72, [[26/21]] | ||
|- | |- | ||
| 20 | | 20 | ||
| Line 122: | Line 122: | ||
| 21 | | 21 | ||
| 400.0 | | 400.0 | ||
| | | [[49/39]], [[44/35]], 39/31, 112/89, 73/58, 92/73, 29/23, 53/42, [[91/72]], 62/49 | ||
|- | |- | ||
| 22 | | 22 | ||
| Line 130: | Line 130: | ||
| 23 | | 23 | ||
| 438.1 | | 438.1 | ||
| ''[[32/25]]'', [[9/7]], 112/87, 94/73, 58/45, 40/31, 31/24 | | ''[[32/25]]'', [[9/7]], 112/87, 94/73, 58/45, 40/31, 31/24 | ||
|- | |- | ||
| 24 | | 24 | ||
| Line 138: | Line 138: | ||
| 25 | | 25 | ||
| 476.19 | | 476.19 | ||
| | | [[21/16]], [[46/35]], 96/73, 29/22, [[120/91]], 62/47, 70/53 | ||
|- | |- | ||
| 26 | | 26 | ||
| 495.24 | | 495.24 | ||
| 93/70, [[4/3]] | | 93/70, [[4/3]] | ||
|- | |- | ||
| 27 | | 27 | ||
| Line 158: | Line 158: | ||
| 30 | | 30 | ||
| 571.43 | | 571.43 | ||
| [[18/13 | | [[18/13]], 43/31, 146/105, 89/64, [[32/23]], [[39/28]], 124/89, [[46/33]], 60/43 | ||
|- | |- | ||
| 31 | | 31 | ||
| Line 170: | Line 170: | ||
| 33 | | 33 | ||
| 628.57 | | 628.57 | ||
| 43/30, [[33/23]], 89/62, [[56/39]], [[23/16]], 128/89, 105/73, 62/43 | | 43/30, [[33/23]], 89/62, [[56/39]], [[23/16]], 128/89, 105/73, 62/43, [[13/9]] | ||
|- | |- | ||
| 34 | | 34 | ||
| Line 186: | Line 186: | ||
| 37 | | 37 | ||
| 704.76 | | 704.76 | ||
| | | [[3/2]], 140/93 | ||
|- | |- | ||
| 38 | | 38 | ||
| 723.81 | | 723.81 | ||
| 53/35, 47/31, [[91/60]], 44/29, 73/48, [[35/23]], [[32/21]] | | 53/35, 47/31, [[91/60]], 44/29, 73/48, [[35/23]], [[32/21]] | ||
|- | |- | ||
| 39 | | 39 | ||
| Line 198: | Line 198: | ||
| 40 | | 40 | ||
| 761.9 | | 761.9 | ||
| | | 48/31, 31/20, 45/29, 73/47, 87/56, [[14/9]], ''[[25/16]]'' | ||
|- | |- | ||
| 41 | | 41 | ||
| Line 206: | Line 206: | ||
| 42 | | 42 | ||
| 800.0 | | 800.0 | ||
| 49/31, [[144/91]], 84/53, 46/29, 73/46, 116/73, 89/56, 62/39, [[35/22]], [[78/49]] | | 49/31, [[144/91]], 84/53, 46/29, 73/46, 116/73, 89/56, 62/39, [[35/22]], [[78/49]] | ||
|- | |- | ||
| 43 | | 43 | ||
| Line 214: | Line 214: | ||
| 44 | | 44 | ||
| 838.1 | | 838.1 | ||
| [[21/13]], 144/89, 47/29, 73/45, 86/53, [[13/8]], 70/43 | | [[21/13]], 144/89, 47/29, 73/45, 86/53, [[13/8]], 70/43 | ||
|- | |- | ||
| 45 | | 45 | ||
| Line 222: | Line 222: | ||
| 46 | | 46 | ||
| 876.19 | | 876.19 | ||
| | | 43/26, 48/29, 53/32, 58/35, 73/44, 78/47, 88/53, 93/56, [[5/3]] | ||
|- | |- | ||
| 47 | | 47 | ||
| Line 230: | Line 230: | ||
| 48 | | 48 | ||
| 914.29 | | 914.29 | ||
| 49/29, [[22/13]], 105/62, 178/105, [[39/23]], [[56/33]], 73/43, 90/53, 124/73 | | 49/29, [[22/13]], 105/62, 178/105, [[39/23]], [[56/33]], 73/43, 90/53, 124/73 | ||
|- | |- | ||
| 49 | | 49 | ||
| 933.33 | | 933.33 | ||
| | | 53/31, 89/52, [[12/7]], 91/53, 31/18, ''50/29'' | ||
|- | |- | ||
| 50 | | 50 | ||
| 952.38 | | 952.38 | ||
| [[45/26]], [[26/15]], 92/53, 73/42 | | [[45/26]], [[26/15]], 92/53, 73/42 | ||
|- | |- | ||
| 51 | | 51 | ||
| Line 282: | Line 282: | ||
| 61 | | 61 | ||
| 1161.9 | | 1161.9 | ||
| | | 84/43, 43/22, 174/89, [[88/45]], 178/91, [[45/23]], 182/93, 92/47, 47/24, [[96/49]], 104/53 | ||
|- | |- | ||
| 62 | | 62 | ||
| 1180.95 | | 1180.95 | ||
| [[63/32]] | | [[63/32]], 144/73, 172/87, 87/44, 176/89, 89/45, [[180/91]], [[91/46]], 184/93, 93/47, [[208/105]], 105/53 | ||
|- | |- | ||
| 63 | | 63 | ||
Revision as of 03:07, 12 March 2025
| ← 62edo | 63edo | 64edo → |
63 equal divisions of the octave (abbreviated 63edo or 63ed2), also called 63-tone equal temperament (63tet) or 63 equal temperament (63et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 63 equal parts of about 19 ¢ each. Each step represents a frequency ratio of 21/63, or the 63rd root of 2.
Theory
63edo tempers out 3125/3072 in the 5-limit and 225/224, 245/243, and 875/864 in the 7-limit, so that it supports magic temperament. In the 11-limit it tempers out 100/99, supporting 11-limit magic, plus 385/384 and 540/539, 896/891. In the 13-limit it tempers out 169/168, 275/273, 640/637, 352/351, 364/363 and 676/675. It provides the optimal patent val for immune, the 29 & 34d temperament in the 7-, 11- and 13-limit.
63 is also a fascinating division to look at in the 47-limit. Although it does not deal as well with primes 5, 17, 19, 37 and 41, it excels in the 2.3.7.11.13.23.29.31.43.47 subgroup, and is a great candidate for a gentle tuning. Its regular augmented fourth (+6 fifths) is less than 0.3 cents sharp of 23/16, therefore tempering out 736/729. Its diesis (+12 fifths) can represent 33/32, 32/31, 30/29, 29/28, 28/27, as well as 91/88, and more, so it is very versatile, making chains of fifths of 12 tones or longer very useful in covering harmonic and melodic ground while providing a lot of different colour in different keys. We can take advantage of the representation of 27:28:29:30:31:32:33, which splits 11/9 into six "small dieses" as a result; here it can be seen more clearly why these are not regular quarter-tones so are best distinguished from such with the qualifier "large", as otherwise we would expect to see some flavour of minor third after six of them.
A 17-tone fifths chain looks on the surface a little similar to 17edo, but as −17 fifths gets us to 64/63, observing the comma becomes an essential part in progressions favouring prime 7. Furthermore, its prime 5 is far from unusable; although 25/16 is barely inconsistent, this affords the tuning supporting 7-limit magic, which may be considered interesting or desirable in of itself. And if this was not enough, if you really want to, it offers reasonable approximations to some yet higher primes too; namely 43/32, 47/32, and 53/32; see the tables below.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | +2.81 | -5.36 | +2.60 | +1.06 | -2.43 | +9.33 | +7.25 | +0.30 | -1.01 | -2.18 | -3.72 |
| Relative (%) | +0.0 | +14.7 | -28.1 | +13.7 | +5.6 | -12.8 | +49.0 | +38.1 | +1.6 | -5.3 | -11.4 | -19.6 | |
| Steps (reduced) |
63 (0) |
100 (37) |
146 (20) |
177 (51) |
218 (29) |
233 (44) |
258 (6) |
268 (16) |
285 (33) |
306 (54) |
312 (60) |
328 (13) | |
| Harmonic | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +9.03 | +2.77 | +1.16 | +2.69 | +7.50 | +6.92 | -3.12 | -8.27 | +0.78 | -2.63 | +7.10 | +0.55 |
| Relative (%) | +47.4 | +14.5 | +6.1 | +14.1 | +39.3 | +36.4 | -16.4 | -43.4 | +4.1 | -13.8 | +37.3 | +2.9 | |
| Steps (reduced) |
338 (23) |
342 (27) |
350 (35) |
361 (46) |
371 (56) |
374 (59) |
382 (4) |
387 (9) |
390 (12) |
397 (19) |
402 (24) |
408 (30) | |
Subsets and supersets
Since 63 factors into 32 × 7, 63edo has subset edos 3, 7, 9, and 21.
Its representation of the 2.3.5.7.13 subgroup (no-11's 13-limit) can uniquely be described in terms of accurate approximations contained in its main subsets of 7edo and 9edo:
- 1\9 = ~14/13~13/12, implying (the much more accurate) 2\9 = ~7/6 (septiennealic)
- 2\7 = ~39/32~128/105, via 4096/4095 and the akjaysma (which are naturally paired)
If we avoid equating 14/13 and 13/12 (which is by far the highest damage equivalence) so that we achieve 7/6 = 2\9 directly, we get the 63 & 441 microtemperament in the same subgroup.
Intervals
The following table was created using Godtone's code with the command interpret_edo(63,ol=53,no=[5,17,19,25,27,37,41,51],add=[73,75,87,89,91,93,105],dec="''",wiki=23) (run in a Python 3 interactive console) plus manual correction of the order of some inconsistent intervals and removal of unsimplified intervals of 75.
As the command and description indicates, it is a(n accurate) "no-5's"* no-17's no-19's no-25's no-27's no-37's no-41's 49-odd-limit add-53 add-63 add-73 add-87 add-89 add-91 add-93 add-105 interpretation, tuned to the strengths of 63edo. * Note that because of the cancellation of factors, some odd harmonics of 5 (the simpler/more relevant ones) are present, EG 75/3 = 25, 45/3 = 15, 105/75 = 7/5, 75/35/2 = 15/14, and 45/9 = 5, so it isn't really "no-5's", just has a de-emphasized focus.
Intervals are listed in order of size, so that one can know their relative order at a glance and deem the value of the interpretation for a harmonic context, and 23-limit intervals are highlighted for navigability as 13-limit intervals are more likely to already have pages, and as we are excluding primes 17 and 19, we are only adding prime 23 to the 13-limit.
Inconsistent intervals are in italics.
| Degree | Cents | Approximate ratios[note 1] |
|---|---|---|
| 0 | 0.0 | 1/1 |
| 1 | 19.05 | 106/105, 105/104, 94/93, 93/92, 92/91, 91/90, 90/89, 89/88, 88/87, 87/86, 73/72, 65/64, 64/63 |
| 2 | 38.1 | 66/65, 53/52, 49/48, 48/47, 47/46, 93/91, 46/45, 91/89, 45/44, 89/87, 44/43, 43/42 |
| 3 | 57.14 | 36/35, 33/32, 32/31, 94/91, 31/30, 92/89, 91/88, 30/29, 89/86, 29/28, 25/24 |
| 4 | 76.19 | 26/25, 49/47, 73/70, 24/23, 47/45, 93/89, 23/22, 91/87, 45/43, 22/21 |
| 5 | 95.24 | 98/93, 96/91, 94/89, 56/53, 93/88, 92/87, 91/86, 89/84, 35/33, 52/49 |
| 6 | 114.29 | 33/31, 49/46, 16/15, 47/44, 78/73, 31/29, 46/43, 15/14 |
| 7 | 133.33 | 14/13, 96/89, 94/87, 93/86, 53/49, 13/12 |
| 8 | 152.38 | 49/45, 12/11, 47/43, 35/32, 58/53, 23/21 |
| 9 | 171.43 | 11/10, 98/89, 43/39, 32/29, 53/48, 116/105, 73/66, 52/47, 31/28 |
| 10 | 190.48 | 49/44, 39/35, 29/26, 48/43, 105/94, 104/93, 47/42 |
| 11 | 209.52 | 28/25, 9/8, 98/87, 53/47, 44/39, 35/31, 26/23, 60/53, 25/22 |
| 12 | 228.57 | 33/29, 49/43, 106/93, 73/64, 89/78, 105/92, 8/7 |
| 13 | 247.62 | 84/73, 53/46, 15/13, 52/45 |
| 14 | 266.67 | 29/25, 36/31, 106/91, 7/6, 104/89, 62/53 |
| 15 | 285.71 | 73/62, 53/45, 86/73, 33/28, 46/39, 105/89, 124/105, 13/11, 58/49 |
| 16 | 304.76 | 106/89, 56/47, 87/73, 31/26, 105/88, 43/36, 104/87 |
| 17 | 323.81 | 6/5, 112/93, 53/44, 47/39, 88/73, 35/29, 64/53, 29/24, 52/43 |
| 18 | 342.86 | 73/60, 28/23, 106/87, 39/32, 128/105, 89/73, 105/86, 11/9, 60/49 |
| 19 | 361.9 | 43/35, 16/13, 53/43, 90/73, 58/47, 89/72, 26/21 |
| 20 | 380.95 | 31/25, 36/29, 87/70, 56/45, 66/53, 91/73, 116/93, 5/4 |
| 21 | 400.0 | 49/39, 44/35, 39/31, 112/89, 73/58, 92/73, 29/23, 53/42, 91/72, 62/49 |
| 22 | 419.05 | 33/26, 89/70, 14/11, 93/73, 116/91, 60/47, 23/18 |
| 23 | 438.1 | 32/25, 9/7, 112/87, 94/73, 58/45, 40/31, 31/24 |
| 24 | 457.14 | 13/10, 56/43, 43/33, 116/89, 73/56, 30/23, 47/36, 64/49 |
| 25 | 476.19 | 21/16, 46/35, 96/73, 29/22, 120/91, 62/47, 70/53 |
| 26 | 495.24 | 93/70, 4/3 |
| 27 | 514.29 | 98/73, 47/35, 43/32, 39/29, 35/26, 66/49, 31/23, 120/89, 89/66, 58/43 |
| 28 | 533.33 | 42/31, 72/53, 53/39, 87/64, 49/36, 64/47, 124/91, 15/11 |
| 29 | 552.38 | 48/35, 11/8, 128/93, 73/53, 62/45, 91/66, 40/29, 29/21 |
| 30 | 571.43 | 18/13, 43/31, 146/105, 89/64, 32/23, 39/28, 124/89, 46/33, 60/43 |
| 31 | 590.48 | 7/5, 87/62, 73/52, 66/47, 45/32, 128/91, 31/22 |
| 32 | 609.52 | 44/31, 91/64, 64/45, 47/33, 104/73, 124/87, 10/7 |
| 33 | 628.57 | 43/30, 33/23, 89/62, 56/39, 23/16, 128/89, 105/73, 62/43, 13/9 |
| 34 | 647.62 | 42/29, 29/20, 132/91, 45/31, 106/73, 93/64, 16/11, 35/24 |
| 35 | 666.67 | 22/15, 91/62, 47/32, 72/49, 128/87, 78/53, 53/36, 31/21 |
| 36 | 685.71 | 43/29, 132/89, 89/60, 46/31, 49/33, 52/35, 58/39, 64/43, 70/47, 73/49 |
| 37 | 704.76 | 3/2, 140/93 |
| 38 | 723.81 | 53/35, 47/31, 91/60, 44/29, 73/48, 35/23, 32/21 |
| 39 | 742.86 | 49/32, 72/47, 23/15, 112/73, 89/58, 66/43, 43/28, 20/13 |
| 40 | 761.9 | 48/31, 31/20, 45/29, 73/47, 87/56, 14/9, 25/16 |
| 41 | 780.95 | 36/23, 47/30, 91/58, 146/93, 11/7, 140/89, 52/33 |
| 42 | 800.0 | 49/31, 144/91, 84/53, 46/29, 73/46, 116/73, 89/56, 62/39, 35/22, 78/49 |
| 43 | 819.05 | 8/5, 93/58, 146/91, 53/33, 45/28, 140/87, 29/18, 50/31 |
| 44 | 838.1 | 21/13, 144/89, 47/29, 73/45, 86/53, 13/8, 70/43 |
| 45 | 857.14 | 49/30, 18/11, 172/105, 146/89, 105/64, 64/39, 87/53, 23/14, 120/73, 150/91 |
| 46 | 876.19 | 43/26, 48/29, 53/32, 58/35, 73/44, 78/47, 88/53, 93/56, 5/3 |
| 47 | 895.24 | 87/52, 72/43, 176/105, 52/31, 146/87, 47/28, 89/53, 150/89 |
| 48 | 914.29 | 49/29, 22/13, 105/62, 178/105, 39/23, 56/33, 73/43, 90/53, 124/73 |
| 49 | 933.33 | 53/31, 89/52, 12/7, 91/53, 31/18, 50/29 |
| 50 | 952.38 | 45/26, 26/15, 92/53, 73/42 |
| 51 | 971.43 | 7/4, 184/105, 156/89, 128/73, 93/53, 86/49, 58/33 |
| 52 | 990.48 | 44/25, 53/30, 23/13, 62/35, 39/22, 94/53, 87/49, 16/9, 25/14 |
| 53 | 1009.52 | 84/47, 93/52, 188/105, 43/24, 52/29, 70/39, 88/49 |
| 54 | 1028.57 | 56/31, 47/26, 132/73, 105/58, 96/53, 29/16, 78/43, 89/49, 20/11 |
| 55 | 1047.62 | 42/23, 53/29, 64/35, 86/47, 11/6, 90/49 |
| 56 | 1066.67 | 24/13, 98/53, 172/93, 87/47, 89/48, 13/7 |
| 57 | 1085.71 | 28/15, 43/23, 58/31, 73/39, 88/47, 15/8, 92/49, 62/33 |
| 58 | 1104.76 | 49/26, 66/35, 168/89, 172/91, 87/46, 176/93, 53/28, 89/47, 91/48, 93/49 |
| 59 | 1123.81 | 21/11, 86/45, 174/91, 44/23, 178/93, 90/47, 23/12, 140/73, 94/49, 25/13 |
| 60 | 1142.86 | 48/25, 56/29, 172/89, 29/15, 176/91, 89/46, 60/31, 91/47, 31/16, 64/33, 35/18 |
| 61 | 1161.9 | 84/43, 43/22, 174/89, 88/45, 178/91, 45/23, 182/93, 92/47, 47/24, 96/49, 104/53 |
| 62 | 1180.95 | 63/32, 144/73, 172/87, 87/44, 176/89, 89/45, 180/91, 91/46, 184/93, 93/47, 208/105, 105/53 |
| 63 | 1200.0 | 2/1 |
- ↑ Based on treating 63edo as a 2.3.5.7.11.13.23.29.31.43.47.53.73.89-subgroup (no-17's no-19's no-37's no-41's 53-limit add-73 add-89 add-105) temperament; other approaches are also possible. Note that due to the error on 5, only low-complexity intervals involving 5 are included here.
Notation
Sagittal notation
This notation uses the same sagittal sequence as 56-EDO.
Evo flavor

Revo flavor

Ups and downs notation
Using Helmholtz–Ellis accidentals, 63edo can be notated using ups and downs notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||||||||||
| Flat symbol |
Approximation to JI
Zeta peak index
| Tuning | Strength | Closest edo | Integer limit | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per octave | Step size (cents) | Height | Integral | Gap | Edo | Octave (cents) | Consistent | Distinct |
| 321zpi | 63.0192885705350 | 19.0417890652143 | 6.768662 | 1.049023 | 15.412920 | 63edo | 1199.63271110850 | 8 | 8 |
Scales
- Approximation of Pelog lima: 6 9 21 6 21
- Timeywimey (original/default tuning): 16 10 7 4 11 5 10
- Sandcastle (original/default tuning): 8 10 8 11 8 8 10
Music
- Improvisation in 12-tone fifths chain (2015)
- those early dreams (2016)
- early dreams 2 (2016)
- Seconds and Otonal Shifts (2016)