(170 intermediate revisions by 14 users not shown) Line 1:
Line 1: <h2>IMPORTED REVISION FROM WIKISPACES</h2>
{{Infobox MOS}}
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
{{ MOS intro}} It is also equal to a degenerate form of [[diasem ]].
: This revision was by author [[User:JosephRuhf|JosephRuhf]] and made on <tt>2012-11-25 21:27:28 UTC</tt>.<br>
: The original revision id was <tt>385899584</tt>.<br>
: The revision comment was: <tt></tt><br>
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">The familiar harmonic entropy minimum with this MOS pattern is [[meantone family#Godzilla|godzilla]], in which a generator is [[8_7|8/7]] or [[7_6|7/6]] (tempered to be the same interval, or even 37/32 if you like) so two of them make a [[4_3|4/3]]. However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament [[Chromatic pairs#semaphore|semaphore]], there is also a weird scale called "[[pseudo-semaphore]]", in which two different flavors of [[3_2|3/2]] exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2.
||||||||||||||||||||||~ Generator ||~ Cents ||~ Comments ||~ ||
|| 1\5 || || || || || || || || || || || 240 ||= ||= ||
|| || || || || || || || || || || 12\59 || 244.068 ||= Pseudo-semaphore is around here ||= ||
|| || || || || || || || || || 11\54 || || 244.444 ||= ||= ||
|| || || || || || || || || 10\49 || || || 244.898 ||= ||= ||
|| || || || || || || || 9\44 || || || || 245.455 ||= ||= ||
|| || || || || || || 8\39 || || || || || 246.154 ||= ||= ||
|| || || || || || 7\34 || || || || || || 247.059 ||= ||= ||
|| || || || || 6\29 || || || || || || || 248.276 ||= ||= ||
|| || || || || || 11\53 || || || || || || 249.057 ||= Semaphore is around here ||= ||
|| || || || 5\24 || || || || || || || || 250 ||= ||= L/s=4:
generators smaller than this are "impractical" ||
|| || || 4\19 || || || || || || || || || 252.632 ||= Godzilla is around here ||= L/s=3:
generators smaller than this may be considered "impractical" ||
|| || 3\14 || || || || || || || || || || 257.143 ||= Boundary of propriety (generators
larger than this are proper) ||= ||
|| || || || 8\37 || || || || || || || || 259.459 ||= ||= ||
|| || || || || || 21\97 || || || || || || 259.794 ||= ||= ||
|| || || || || || || || 55\254 || || || || 259.843 ||= ||= ||
|| || || || || || || || || || 144\665 || || 259.850 ||= ||= ||
|| || || || || || || || || || || 233\1076 || 259.851 ||= Golden [[superpelog]] ||= ||
|| || || || || || || || || 89\411 || || || 259.854 ||= ||= ||
|| || || || || || || 34\157 || || || || || 259.873 ||= ||= ||
|| || || || || 13\60 || || || || || || || 260 ||= ||= ||
|| || || 5\23 || || || || || || || || || 260.870 ||= Optimum rank range (L/s=3/2) superpelog ||= ||
|| || || || 7\32 || || || || || || || || 262.5 ||= ||= ||
|| || || || || 9\41 || || || || || || || 263.415 ||= ||= ||
|| || || || || || 11\50 || || || || || || 264 ||= ||= ||
|| || || || || || || 13\59 || || || || || 264.407 ||= ||= ||
|| || || || || || || || 15\68 || || || || 264.706 ||= ||= ||
|| || || || || || || || || 17\77 || || || 264.935 ||= ||= ||
|| || || || || || || || || || 19\86 || || 265.116 ||= ||= ||
|| || || || || || || || || || || 21\95 || 265.263 ||= ||= ||
|| 2\9 || || || || || || || || || || || 266.667 ||= ||= ||</pre></div>
<h4>Original HTML content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html"><html><head><title>5L 4s</title></head><body>The familiar harmonic entropy minimum with this MOS pattern is <a class="wiki_link" href="/meantone%20family#Godzilla">godzilla</a>, in which a generator is <a class="wiki_link" href="/8_7">8/7</a> or <a class="wiki_link" href="/7_6">7/6</a> (tempered to be the same interval, or even 37/32 if you like) so two of them make a <a class="wiki_link" href="/4_3">4/3</a>. However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament <a class="wiki_link" href="/Chromatic%20pairs#semaphore">semaphore</a>, there is also a weird scale called &quot;<a class="wiki_link" href="/pseudo-semaphore">pseudo-semaphore</a>&quot;, in which two different flavors of <a class="wiki_link" href="/3_2">3/2</a> exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2.<br />
== Names ==
The [[TAMNAMS]] convention, used by this article, uses '''semiquartal''' (derived from 'half a fourth') for the 5L 4s pattern. Another attested name is '''hemifourths'''.
<table class="wiki_table">
== Scale properties ==
<tr>
{{TAMNAMS use}}
<th colspan="11">Generator<br />
</th>
<th>Cents<br />
</th>
<th>Comments<br />
</th>
<th><br />
</th>
</tr>
<tr>
<td>1\5<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>240<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>12\59<br />
</td>
<td>244.068<br />
</td>
<td style="text-align: center;">Pseudo-semaphore is around here<br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>11\54<br />
</td>
<td><br />
</td>
<td>244.444<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>10\49<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>244.898<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>9\44<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>245.455<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>8\39<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>246.154<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>7\34<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>247.059<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>6\29<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>248.276<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>11\53<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>249.057<br />
</td>
<td style="text-align: center;">Semaphore is around here<br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>5\24<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>250<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;">L/s=4:<br />
generators smaller than this are &quot;impractical&quot;<br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td>4\19<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>252.632<br />
</td>
<td style="text-align: center;">Godzilla is around here<br />
</td>
<td style="text-align: center;">L/s=3:<br />
generators smaller than this may be considered &quot;impractical&quot;<br />
</td>
</tr>
<tr>
<td><br />
</td>
<td>3\14<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>257.143<br />
</td>
<td style="text-align: center;">Boundary of propriety (generators<br />
larger than this are proper)<br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>8\37<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>259.459<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>21\97<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>259.794<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>55\254<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>259.843<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>144\665<br />
</td>
<td><br />
</td>
<td>259.850<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>233\1076<br />
</td>
<td>259.851<br />
</td>
<td style="text-align: center;">Golden <a class="wiki_link" href="/superpelog">superpelog</a><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>89\411<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>259.854<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>34\157<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>259.873<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>13\60<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>260<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td>5\23<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>260.870<br />
</td>
<td style="text-align: center;">Optimum rank range (L/s=3/2) superpelog<br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>7\32<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>262.5<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>9\41<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>263.415<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>11\50<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>264<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>13\59<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>264.407<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>15\68<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>264.706<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>17\77<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>264.935<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>19\86<br />
</td>
<td><br />
</td>
<td>265.116<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>21\95<br />
</td>
<td>265.263<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
<tr>
<td>2\9<br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td><br />
</td>
<td>266.667<br />
</td>
<td style="text-align: center;"><br />
</td>
<td style="text-align: center;"><br />
</td>
</tr>
</table>
</body></html></pre></div>
=== Intervals ===
{{MOS intervals}}
=== Generator chain ===
{{MOS genchain}}
=== Modes ===
{{MOS mode degrees}}
Note that the darkest two modes have no diatonic or [[armotonic]] fifth on the root in nonextreme semiquartal tunings.
== Theory ==
The harmonic entropy minimum with this MOS pattern is [[godzilla]], in which the generator tempers [[8/7]] or [[7/6]] to be the same interval, and two generators is [[4/3]]. However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament [[semaphore]], there is also a weird scale called "[[pseudo-semaphore]]", in which two different flavors of [[3/2]] exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2. The 2.3.13/5 [[barbados]] temperament is another possible interpretation.
== Tuning ranges ==
=== Hard-of-basic ===
Hard-of-basic tunings have [[semifourth]]s as generators, between 1\5 (240{{c}}) and 3\14 (257.14{{c}}), where two of them create a diatonic 4th. The generator could be viewed as a 15/13, and the resulting "inframinor" and "ultramajor" chords and triads could be viewed as approximating, respectively, 26:30:39 and 10:13:15 (see [[Arto and tendo theory]]).
==== Hypohard ====
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard ({{nowrap|2/1 ≤ L/s ≤ 3/1}}) tunings.
{| class="wikitable right-2 right-3 right-4 right-5 right-6"
|-
!
! [[14edo]] ({{nowrap|L/s {{=}} 2/1}})
! [[47edo]] ({{nowrap|L/s {{=}} 7/3}})
! [[33edo]] ({{nowrap|L/s {{=}} 5/2}})
! [[52edo]] ({{nowrap|L/s {{=}} 8/3}})
! [[19edo]] ({{nowrap|L/s {{=}} 3/1}})
|-
| Generator (g)
| 3\14, 257.14
| 10\47, 255.32
| 7\33, 254.54
| 11\52, 253.85
| 4\19, 252.63
|-
| L ({{nowrap|octave − 4g}})
| 171.43
| 178.72
| 181.81
| 184.62
| 189.47
|-
| s ({{nowrap|5g − octave}})
| 85.71
| 76.60
| 72.73
| 69.23
| 63.16
|}
This range is notable for having many simple tunings that are close to being "eigentunings" (tunings that tune a certain JI interval exactly):
* 33edo semiquartal has close 7/5 (error −0.69{{c}}), 9/5 (error −0.59{{c}}) and 9/7 (error +1.28{{c}}), thus can be used for the close 5:7:9 in the two Locrian-like modes 1|7 and 0|8
* 52edo semiquartal has close 22/19 (error +0.04{{c}})
* 19edo semiquartal has close 6/5 (error +0.15{{c}}) and 28/27 (error +0.20{{c}})
However, for the more complex intervals such as 22/19 and 28/27, you might want to use the exact eigentuning for the full effect, unless you specifically need an edo for modulatory purposes.
==== Parahard and ultrahard ====
One important sub-range is given by stipulating that two semifourth generators must make a ''meantone'' fourth; i.e. that four fifths should approximate a [[5/4]] major third. This can be considered the [[19edo]] (4\19)-to-[[24edo]] (5\24) range, i.e. parahard semiquartal, which also contains [[43edo]] (9\43) and [[62edo]] (13\62). Parahard semiquartal can be given an RTT interpretation known as [[godzilla]].
The sizes of the generator, large step and small step of 5L   ;4s are as follows in various hypohard ({{nowrap|2 /1 &le ; L/s &le ; 3/1}}) tunings.
{| class="wikitable right-2 right-3 right-4 right-5"
|-
!
! [[19edo]]
! [[24edo]]
! [[29edo]]
|-
| Generator (g)
| 4\19, 252.63
| 5\24, 250.00
| 6\29, 248.28
|-
| L ({{nowrap|octave − 4g}})
| 189.47
| 200.00
| 206.90
|-
| s ({{nowrap|5g − octave}})
| 63.16
| 50.00
| 41.38
|}
=== Soft-of-basic ===
Soft-of-basic tunings have semifourths that are between 3\14 (257.14{{c}}) and 2\9 (266.67{{c}}), creating a "[[mavila]]" or "[[superdiatonic]]" 4th. [[23edo]]'s 5\23 (260.87{{c}}) is an example of this generator.
The sizes of the generator, large step and small step of 5L 4s are as follows in various soft-of-basic tunings.
{| class="wikitable right-2 right-3 right-4 right-5"
|-
!
! [[23edo]]
! [[32edo]]
! [[37edo]]
|-
| Generator (g)
| 5\23, 260.87
| 7\32, 262.50
| 8\37, 259.46
|-
| L ({{nowrap|octave − 4g}})
| 156.52
| 150.00
| 162.16
|-
| s ({{nowrap|5g − octave}})
| 104.35
| 112.50
| 97.30
|}
=== Tuning examples ===
An example in the Diasem Lydian mode LSLSLMLSLM with M and S equated. ([[:File:Diasem Lydian Example Score.pdf|score]])
[[File:Diasem Lydian Example 14edo.mp3]] [[14edo]], [[basic]] semiquartal
[[File:Diasem Lydian Example 19edo.mp3]] [[19edo]], [[hard]] semiquartal
[[File:Diasem Lydian Example 23edo.mp3]] [[23edo]], [[soft]] semiquartal
[[File:Diasem Lydian Example 24edo.mp3]] [[24edo]], [[superhard]] semiquartal
[[File:Diasem Lydian Example 33edo semiquartal.mp3]] [[33edo]], [[semihard]] semiquartal
== Scale tree ==
{{MOS tuning spectrum
| 5/4 = Septimin
| 4/3 = Beep
| 3/2 = Bug
| 13 /8 = Golden bug
| 13/5 = Golden semaphore
| 3/1 = Godzilla
| 11/3 = Semaphore
}}
== Gallery ==
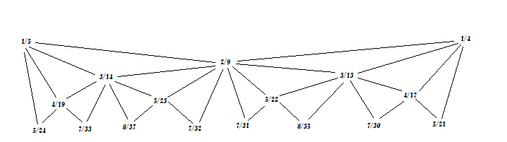
[[File:Hemifourths.png|thumb|An alternative diagram with branch depth = 5|alt=|none|507x507px]]
A voice-leading sketch in [[24edo]] by [[Jacob Barton]]:
[[File:qt_mode_chord_prog.mp3|qt mode chord prog]]
== Music ==
* [https://www.soundclick.com/bands/songInfo.cfm?bandID=376205 &songID=5327098 ''Entropy, the Grandfather of Wind''] (broken link. 2011-03-04) In [[14edo]]{{dead link}}
; [[Frédéric Gagné]]
* ''Whalectric'' (2022) – [https://youtu.be/_E6qvbJWYY8 YouTube] | [https://musescore.com/fredg999/whalectric score] – In [[51edo]], 4|4 mode
; [[Inthar]]
* [[:File:Dream EP 14edo Sketch.mp3|''Dream EP 14edo Sketch'']] (2021) – A short swing ditty in [[14edo]], in the 212121221 mode
* [[:File:19edo Semaphore Fugue.mp3|''19edo Semaphore Fugue'']] (2021) – An unfinished fugue in [[19edo]], in the 212121221 mode
; [[Starshine]]
* [https://soundcloud.com/starshine99/rins-ufo-ride ''Rin's UFO Ride''] (2020) – Semaphore[9] in [[19edo]]
; [[Sevish]]
* [http://www.youtube.com /watch?v=Gcgawrr2xao ''Desert Island Rain''] – Semaphore[9] in [[313edo]] using 65\313 as the generator
[[Category:Semiquartal| ]] <!-- Main article -- >
5L 4s , named semiquartal in TAMNAMS , is a 2/1-equivalent (octave-equivalent ) moment of symmetry scale containing 5 large steps and 4 small steps, repeating every octave . Generators that produce this scale range from 933.3 ¢ to 960 ¢ , or from 240 ¢ to 266.7 ¢ . It is also equal to a degenerate form of diasem .
Names The TAMNAMS convention, used by this article, uses semiquartal (derived from 'half a fourth') for the 5L 4s pattern. Another attested name is hemifourths .
Scale properties This article uses TAMNAMS conventions for the names of this scale's intervals and scale degrees . The use of 1-indexed ordinal names is reserved for interval regions. Intervals
Intervals of 5L 4s
Intervals
Steps
Range in cents
Generic
Specific
Abbrev.
0-cthonstep
Perfect 0-cthonstep
P0cts
0
0.0 ¢
1-cthonstep
Minor 1-cthonstep
m1cts
s
0.0 ¢ to 133.3 ¢
Major 1-cthonstep
M1cts
L
133.3 ¢ to 240.0 ¢
2-cthonstep
Perfect 2-cthonstep
P2cts
L + s
240.0 ¢ to 266.7 ¢
Augmented 2-cthonstep
A2cts
2L
266.7 ¢ to 480.0 ¢
3-cthonstep
Minor 3-cthonstep
m3cts
L + 2s
240.0 ¢ to 400.0 ¢
Major 3-cthonstep
M3cts
2L + s
400.0 ¢ to 480.0 ¢
4-cthonstep
Minor 4-cthonstep
m4cts
2L + 2s
480.0 ¢ to 533.3 ¢
Major 4-cthonstep
M4cts
3L + s
533.3 ¢ to 720.0 ¢
5-cthonstep
Minor 5-cthonstep
m5cts
2L + 3s
480.0 ¢ to 666.7 ¢
Major 5-cthonstep
M5cts
3L + 2s
666.7 ¢ to 720.0 ¢
6-cthonstep
Minor 6-cthonstep
m6cts
3L + 3s
720.0 ¢ to 800.0 ¢
Major 6-cthonstep
M6cts
4L + 2s
800.0 ¢ to 960.0 ¢
7-cthonstep
Diminished 7-cthonstep
d7cts
3L + 4s
720.0 ¢ to 933.3 ¢
Perfect 7-cthonstep
P7cts
4L + 3s
933.3 ¢ to 960.0 ¢
8-cthonstep
Minor 8-cthonstep
m8cts
4L + 4s
960.0 ¢ to 1066.7 ¢
Major 8-cthonstep
M8cts
5L + 3s
1066.7 ¢ to 1200.0 ¢
9-cthonstep
Perfect 9-cthonstep
P9cts
5L + 4s
1200.0 ¢
Generator chain
Generator chain of 5L 4s
Bright gens
Scale degree
Abbrev.
13
Augmented 1-cthondegree
A1ctd
12
Augmented 3-cthondegree
A3ctd
11
Augmented 5-cthondegree
A5ctd
10
Augmented 7-cthondegree
A7ctd
9
Augmented 0-cthondegree
A0ctd
8
Augmented 2-cthondegree
A2ctd
7
Major 4-cthondegree
M4ctd
6
Major 6-cthondegree
M6ctd
5
Major 8-cthondegree
M8ctd
4
Major 1-cthondegree
M1ctd
3
Major 3-cthondegree
M3ctd
2
Major 5-cthondegree
M5ctd
1
Perfect 7-cthondegree
P7ctd
0
Perfect 0-cthondegree
P0ctd
−1
Perfect 2-cthondegree
P2ctd
−2
Minor 4-cthondegree
m4ctd
−3
Minor 6-cthondegree
m6ctd
−4
Minor 8-cthondegree
m8ctd
−5
Minor 1-cthondegree
m1ctd
−6
Minor 3-cthondegree
m3ctd
−7
Minor 5-cthondegree
m5ctd
−8
Diminished 7-cthondegree
d7ctd
−9
Diminished 9-cthondegree
d9ctd
−10
Diminished 2-cthondegree
d2ctd
−11
Diminished 4-cthondegree
d4ctd
−12
Diminished 6-cthondegree
d6ctd
−13
Diminished 8-cthondegree
d8ctd
Modes
Scale degrees of the modes of 5L 4s
UDP
Cyclic
Step
Scale degree (cthondegree)
0
1
2
3
4
5
6
7
8
9
8|0
1
LLsLsLsLs
Perf.
Maj.
Aug.
Maj.
Maj.
Maj.
Maj.
Perf.
Maj.
Perf.
7|1
8
LsLLsLsLs
Perf.
Maj.
Perf.
Maj.
Maj.
Maj.
Maj.
Perf.
Maj.
Perf.
6|2
6
LsLsLLsLs
Perf.
Maj.
Perf.
Maj.
Min.
Maj.
Maj.
Perf.
Maj.
Perf.
5|3
4
LsLsLsLLs
Perf.
Maj.
Perf.
Maj.
Min.
Maj.
Min.
Perf.
Maj.
Perf.
4|4
2
LsLsLsLsL
Perf.
Maj.
Perf.
Maj.
Min.
Maj.
Min.
Perf.
Min.
Perf.
3|5
9
sLLsLsLsL
Perf.
Min.
Perf.
Maj.
Min.
Maj.
Min.
Perf.
Min.
Perf.
2|6
7
sLsLLsLsL
Perf.
Min.
Perf.
Min.
Min.
Maj.
Min.
Perf.
Min.
Perf.
1|7
5
sLsLsLLsL
Perf.
Min.
Perf.
Min.
Min.
Min.
Min.
Perf.
Min.
Perf.
0|8
3
sLsLsLsLL
Perf.
Min.
Perf.
Min.
Min.
Min.
Min.
Dim.
Min.
Perf.
Note that the darkest two modes have no diatonic or armotonic fifth on the root in nonextreme semiquartal tunings.
Theory The harmonic entropy minimum with this MOS pattern is godzilla , in which the generator tempers 8/7 or 7/6 to be the same interval, and two generators is 4/3 . However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament semaphore , there is also a weird scale called "pseudo-semaphore ", in which two different flavors of 3/2 exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2. The 2.3.13/5 barbados temperament is another possible interpretation.
Tuning ranges Hard-of-basic Hard-of-basic tunings have semifourths as generators, between 1\5 (240 ¢) and 3\14 (257.14 ¢), where two of them create a diatonic 4th. The generator could be viewed as a 15/13, and the resulting "inframinor" and "ultramajor" chords and triads could be viewed as approximating, respectively, 26:30:39 and 10:13:15 (see Arto and tendo theory ).
Hypohard The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard (2/1 ≤ L/s ≤ 3/1 ) tunings.
14edo (L/s = 2/1 )
47edo (L/s = 7/3 )
33edo (L/s = 5/2 )
52edo (L/s = 8/3 )
19edo (L/s = 3/1 )
Generator (g)
3\14, 257.14
10\47, 255.32
7\33, 254.54
11\52, 253.85
4\19, 252.63
L (octave − 4g )
171.43
178.72
181.81
184.62
189.47
s (5g − octave )
85.71
76.60
72.73
69.23
63.16
This range is notable for having many simple tunings that are close to being "eigentunings" (tunings that tune a certain JI interval exactly):
33edo semiquartal has close 7/5 (error −0.69 ¢), 9/5 (error −0.59 ¢) and 9/7 (error +1.28 ¢), thus can be used for the close 5:7:9 in the two Locrian-like modes 1|7 and 0|8
52edo semiquartal has close 22/19 (error +0.04 ¢)
19edo semiquartal has close 6/5 (error +0.15 ¢) and 28/27 (error +0.20 ¢) However, for the more complex intervals such as 22/19 and 28/27, you might want to use the exact eigentuning for the full effect, unless you specifically need an edo for modulatory purposes.
Parahard and ultrahard One important sub-range is given by stipulating that two semifourth generators must make a meantone fourth; i.e. that four fifths should approximate a 5/4 major third. This can be considered the 19edo (4\19)-to-24edo (5\24) range, i.e. parahard semiquartal, which also contains 43edo (9\43) and 62edo (13\62). Parahard semiquartal can be given an RTT interpretation known as godzilla .
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard (2/1 ≤ L/s ≤ 3/1 ) tunings.
19edo
24edo
29edo
Generator (g)
4\19, 252.63
5\24, 250.00
6\29, 248.28
L (octave − 4g )
189.47
200.00
206.90
s (5g − octave )
63.16
50.00
41.38
Soft-of-basic Soft-of-basic tunings have semifourths that are between 3\14 (257.14 ¢) and 2\9 (266.67 ¢), creating a "mavila " or "superdiatonic " 4th. 23edo 's 5\23 (260.87 ¢) is an example of this generator.
The sizes of the generator, large step and small step of 5L 4s are as follows in various soft-of-basic tunings.
23edo
32edo
37edo
Generator (g)
5\23, 260.87
7\32, 262.50
8\37, 259.46
L (octave − 4g )
156.52
150.00
162.16
s (5g − octave )
104.35
112.50
97.30
Tuning examples An example in the Diasem Lydian mode LSLSLMLSLM with M and S equated. (score )
https://en.xen.wiki/w/File:Diasem_Lydian_Example_14edo.mp3 14edo , basic semiquartal
https://en.xen.wiki/w/File:Diasem_Lydian_Example_19edo.mp3 19edo , hard semiquartal
https://en.xen.wiki/w/File:Diasem_Lydian_Example_23edo.mp3 23edo , soft semiquartal
https://en.xen.wiki/w/File:Diasem_Lydian_Example_24edo.mp3 24edo , superhard semiquartal
https://en.xen.wiki/w/File:Diasem_Lydian_Example_33edo_semiquartal.mp3 33edo , semihard semiquartal
Scale tree
Scale tree and tuning spectrum of 5L 4s
Generator(edo)
Cents
Step ratio
Comments
Bright
Dark
L:s
Hardness
7\9
933.333
266.667
1:1
1.000
Equalized 5L 4s
39\50
936.000
264.000
6:5
1.200
32\41
936.585
263.415
5:4
1.250
Septimin
57\73
936.986
263.014
9:7
1.286
25\32
937.500
262.500
4:3
1.333
Supersoft 5L 4s
68\87
937.931
262.069
11:8
1.375
43\55
938.182
261.818
7:5
1.400
61\78
938.462
261.538
10:7
1.429
18\23
939.130
260.870
3:2
1.500
Soft 5L 4s
65\83
939.759
260.241
11:7
1.571
47\60
940.000
260.000
8:5
1.600
76\97
940.206
259.794
13:8
1.625
Golden bug
29\37
940.541
259.459
5:3
1.667
Semisoft 5L 4s
69\88
940.909
259.091
12:7
1.714
40\51
941.176
258.824
7:4
1.750
51\65
941.538
258.462
9:5
1.800
11\14
942.857
257.143
2:1
2.000
Basic 5L 4s
48\61
944.262
255.738
9:4
2.250
37\47
944.681
255.319
7:3
2.333
63\80
945.000
255.000
12:5
2.400
26\33
945.455
254.545
5:2
2.500
Semihard 5L 4s
67\85
945.882
254.118
13:5
2.600
Golden semaphore
41\52
946.154
253.846
8:3
2.667
56\71
946.479
253.521
11:4
2.750
15\19
947.368
252.632
3:1
3.000
Hard 5L 4s
49\62
948.387
251.613
10:3
3.333
34\43
948.837
251.163
7:2
3.500
53\67
949.254
250.746
11:3
3.667
Semaphore
19\24
950.000
250.000
4:1
4.000
Superhard 5L 4s
42\53
950.943
249.057
9:2
4.500
23\29
951.724
248.276
5:1
5.000
27\34
952.941
247.059
6:1
6.000
4\5
960.000
240.000
1:0
→ ∞
Collapsed 5L 4s
Gallery An alternative diagram with branch depth = 5 A voice-leading sketch in 24edo by Jacob Barton :
https://en.xen.wiki/w/File:Qt_mode_chord_prog.mp3
Music Frédéric Gagné Inthar Starshine Sevish