23-limit: Difference between revisions
provided a possible rationale for theoretical interest in this limit |
→Edo approximation: calibrate the list according to my research results |
||
| (26 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
{{Prime limit navigation|23}} | |||
The '''23-limit''' consists of [[just intonation]] [[interval]]s whose [[ratio]]s contain no [[prime factor]]s higher than 23. It is the 9th [[prime limit]] and is a superset of the [[19-limit]] and a subset of the [[29-limit]]. | |||
The 23-limit is a rank-9 system, and can be modeled in a 8-dimensional lattice, with the primes 3, 5, 7, 11, 13, 17, 19, and 23 represented by each dimension. The prime 2 does not appear in the typical 23-limit lattice because [[octave equivalence]] is presumed. If octave equivalence is not presumed, a ninth dimension is needed. | |||
The prime 23 is significant as being the start of a record prime gap ending at 29, the previous record prime gap being the one corresponding to the [[7-limit]]. Thus, it is arguably a potential ideal stopping point for [[prime limit]]s due to a substantial increment in its harmonic contents. Specifically, these things are contained by the 23-limit, but not the 19-limit: | |||
* The [[23-odd-limit|23-]], [[25-odd-limit|25-]], and [[27-odd-limit]]; | |||
* Mode 12, 13, and 14 of the harmonic or subharmonic series. | |||
23 | == Edo approximation == | ||
Here is a list of [[edo]]s with progressively better tunings for 23-limit intervals ([[monotonicity limit]] ≥ 23 and decreasing [[TE error]]): {{EDOs| 58hi, 62, 68e, 72, 94, 111, 121i, 130, 140, 152fg, 159, 183, 190g, 193, 217, 243e, 270, 282, 311, 373g, 422, 525, 566g, 581, 718, 742i, 814, 935, 954h, 1106, 1178, 1308, 1323, 1395, 1506hi, 1578, 1889, 2000, 2460 }} and so on. For a more comprehensive list, see [[Sequence of equal temperaments by error]]. | |||
23 | Here is a list of edos which provides relatively good tunings for 23-limit intervals ([[TE relative error]] < 5%): {{EDOs| 94, 190g, 193, 217, 243e, 270, 282, 311, 328h, 373g, 388, 422, 436, 460, 525, 540, 566g, 581, 624, 639h, 643i, 653, 692i, 718, 742i, 764(h), 814, 860, 882, 908, 935, 954h, 997, 1012, 1046dgh, 1075, 1106, 1125, 1178, 1205g, 1224, 1236(h), 1258, 1282, 1308, 1323, 1357efhi, 1385, 1395, 1419, 1448(g), 1506hi, 1578, 1600, 1646, 1672h, 1677e, 1696, 1718, 1730(g), 1759, 1768gi, 1817hi, 1821ef, 1889, 1920, 1966, 2000, 2038, 2041, 2072, 2087h, 2103, 2113, 2132eh, 2159, 2217, 2231, 2243e, 2270i, 2311, 2320, 2414, 2460 }} and so on. | ||
: '''Note''': [[wart notation]] is used to specify the [[val]] chosen for the edo. In the above list, "58hi" means taking the second closest approximations of harmonics 19 and 23. | |||
23 | [[94edo]] is the first [[edo]] to be consistent in the [[23-odd-limit]]. The smallest edo where the [[23-odd-limit]] is distinctly consistent, meaning each element of the tonality diamond is distinguished, is [[282edo]], although [[311edo]] may be preferred for excellent consistency in much larger odd limits, and thus is a good choice if you want the 23-odd-limit to be distinctly consistent and the 27-odd-limit (and higher) to be consistent. | ||
23/ | == 23-odd-limit intervals == | ||
[[File:Some 23-limit otonal chords.png|thumb|15 pentads and 1 hexad, with 23 as the highest odd harmonic, avoiding steps smaller than 23/21.]] | |||
Ratios of 23 in the 23-odd-limit are: | |||
23/ | {| class="wikitable" | ||
! Ratio | |||
! Cents Value | |||
! colspan="2" | Color Name | |||
! Interval Name | |||
|- | |||
| [[24/23]] | |||
| 73.681¢ | |||
| 23u1 | |||
| twethu 1sn | |||
| lesser vicesimotertial semitone | |||
|- | |||
| [[23/22]] | |||
| 76.956¢ | |||
| 23o1u2 | |||
| twetholu 2nd | |||
| greater vicesimotertial semitone | |||
|- | |||
| [[23/21]] | |||
| 157.493¢ | |||
| 23or2 | |||
| twethoru 2nd | |||
| large vicesimotertial neutral second | |||
|- | |||
| [[26/23]] | |||
| 212.253¢ | |||
| 23u3o2 | |||
| twethutho 2nd | |||
| vicesimotertial whole tone | |||
|- | |||
| [[23/20]] | |||
| 241.961¢ | |||
| 23og3 | |||
| twethogu 3rd | |||
| vicesimotertial inframinor third | |||
|- | |||
| [[23/19]] | |||
| 330.761¢ | |||
| 23o19u3 | |||
| twethonu 3rd | |||
| vicesimotertial supraminor third | |||
|- | |||
| [[28/23]] | |||
| 340.552¢ | |||
| 23uz3 | |||
| twethuzo 3rd | |||
| vicesimotertial neutral third | |||
|- | |||
| [[23/18]] | |||
| 424.364¢ | |||
| 23o4 | |||
| twetho 4th | |||
| vicesimotertial diminished fourth | |||
|- | |||
| [[30/23]] | |||
| 459.994¢ | |||
| 23uy3 | |||
| twethuyo 3rd | |||
| vicesimotertial ultramajor third | |||
|- | |||
| [[23/17]] | |||
| 523.319¢ | |||
| 23o17u4 | |||
| twethosu 4th | |||
| vicesimotertial acute fourth | |||
|- | |||
| [[32/23]] | |||
| 571.726¢ | |||
| 23u4 | |||
| twethu 4th | |||
| vicesimotertial narrow tritone | |||
|- | |||
| [[23/16]] | |||
| 628.274¢ | |||
| 23o5 | |||
| twetho 5th | |||
| vicesimotertial wide tritone | |||
|- | |||
| [[34/23]] | |||
| 676.681¢ | |||
| 23u17o5 | |||
| twethuso 5th | |||
| vicesimotertial grave fifth | |||
|- | |||
| [[23/15]] | |||
| 740.006¢ | |||
| 23og6 | |||
| twethogu 6th | |||
| vicesimotertial ultraminor sixth | |||
|- | |||
| [[36/23]] | |||
| 775.636¢ | |||
| 23u5 | |||
| twethu 5th | |||
| vicesimotertial augmented fifth | |||
|- | |||
| [[23/14]] | |||
| 859.448¢ | |||
| 23or6 | |||
| twethoru 6th | |||
| vicesimotertial neutral sixth | |||
|- | |||
| [[38/23]] | |||
| 869.239¢ | |||
| 23u19o6 | |||
| twethuno 6th | |||
| vicesimotertial submajor sixth | |||
|- | |||
| [[40/23]] | |||
| 958.039¢ | |||
| 23uy6 | |||
| twethuyo 6th | |||
| vicesimotertial ultramajor sixth | |||
|- | |||
| [[23/13]] | |||
| 987.747¢ | |||
| 23o3u7 | |||
| twethothu 7th | |||
| vicesimotertial minor seventh | |||
|- | |||
| [[42/23]] | |||
| 1042.507¢ | |||
| 23uz7 | |||
| twethuzo 7th | |||
| small vicesimotertial neutral seventh | |||
|- | |||
| [[44/23]] | |||
| 1123.044¢ | |||
| 23u1o7 | |||
| twethulo 7th | |||
| vicesimotertial major seventh | |||
|- | |||
| [[23/12]] | |||
| 1126.391¢ | |||
| 23o8 | |||
| twetho 8ve | |||
| vicesimotertial major seventh | |||
|} | |||
== Trivia == | |||
* Unlike most other prime limits, the smallest [[superparticular ratio]] of [[Harmonic class|HC23]] is larger than the smallest one of HC19. 23 is the first prime limit to show this phenomenon. The ratio is, in fact, larger than the second smallest one of HC19. See [[List of superparticular intervals]]. | |||
== Music == | |||
; [[Domin]] | |||
* [https://www.youtube.com/watch?v=RzHkfoa4m3g ''Uttuagn''] (2024) | |||
; [[Francium]] | |||
* "GAY SAPIENS" from ''CAPSLOCK'' (2024) – [https://open.spotify.com/track/5vILBQgWJduJf2ctGGbyUv Spotify] | [https://francium223.bandcamp.com/track/gay-sapiens Bandcamp] | [https://www.youtube.com/watch?v=DHiwdGuZRII YouTube] | |||
; {{W|Franz Liszt}} | |||
* [https://www.youtube.com/watch?v=EOIFIl5D-JE ''Liebestraum No. 3''] (1850) – rendered by Randy Wells (2021) | |||
; [[Randy Wells]] | |||
* [https://www.youtube.com/watch?v=FRy9CePMcJs ''Siren (Waterhouse)''] (2021) | |||
* [https://www.youtube.com/watch?v=Jq_q51vVn4w ''Wilson/Nelson''] (2021) | |||
* [https://www.youtube.com/watch?v=8Jk0KHGawgA ''Laudanum''] (2022) | |||
* [https://www.youtube.com/watch?v=q43e8FhJcRI ''Koi Hito''] (2022) | |||
* [https://www.youtube.com/watch?v=WP5rsOHRWpw ''Hazybrew''] (2022) | |||
* [https://www.youtube.com/watch?v=Qb6IGHzuAtM ''Roses and Wolfsbane''] (2022) | |||
* [https://www.youtube.com/watch?v=ahMoa0R4EjE ''2049: A Love Song''] (2022) | |||
* [https://www.youtube.com/watch?v=NG5XJxV2d2M ''We're a Midwest Emo Intro Waiting to Happen''] (2023) | |||
* [https://www.youtube.com/watch?v=mBlrFTf9Bec ''Phonograph Needle on an Ice Giant's Rings''] (2023) | |||
* [https://www.youtube.com/watch?v=kgovRP0UAfw ''A Cosmic Turtle Grazing Upon Stellar Elements''] (2023) | |||
* [https://www.youtube.com/watch?v=m9QaxFOlnYg ''A Hycean World''] (2023) | |||
* [https://www.youtube.com/watch?v=jpHylRu6XLM ''ser0tonin circuits in a neural network''] (2023) | |||
; {{W|Noah Dean DaSilva Jordan}} | |||
* [https://open.spotify.com/album/2OGG4tT7INfj7iBeN09KDJ Gracias a Dios] (2023) for solo jarana (series 23/22, 23/21....23/12) | |||
[[Category:23-limit| ]] <!-- main article --> | |||
Latest revision as of 16:20, 20 August 2025
The 23-limit consists of just intonation intervals whose ratios contain no prime factors higher than 23. It is the 9th prime limit and is a superset of the 19-limit and a subset of the 29-limit.
The 23-limit is a rank-9 system, and can be modeled in a 8-dimensional lattice, with the primes 3, 5, 7, 11, 13, 17, 19, and 23 represented by each dimension. The prime 2 does not appear in the typical 23-limit lattice because octave equivalence is presumed. If octave equivalence is not presumed, a ninth dimension is needed.
The prime 23 is significant as being the start of a record prime gap ending at 29, the previous record prime gap being the one corresponding to the 7-limit. Thus, it is arguably a potential ideal stopping point for prime limits due to a substantial increment in its harmonic contents. Specifically, these things are contained by the 23-limit, but not the 19-limit:
- The 23-, 25-, and 27-odd-limit;
- Mode 12, 13, and 14 of the harmonic or subharmonic series.
Edo approximation
Here is a list of edos with progressively better tunings for 23-limit intervals (monotonicity limit ≥ 23 and decreasing TE error): 58hi, 62, 68e, 72, 94, 111, 121i, 130, 140, 152fg, 159, 183, 190g, 193, 217, 243e, 270, 282, 311, 373g, 422, 525, 566g, 581, 718, 742i, 814, 935, 954h, 1106, 1178, 1308, 1323, 1395, 1506hi, 1578, 1889, 2000, 2460 and so on. For a more comprehensive list, see Sequence of equal temperaments by error.
Here is a list of edos which provides relatively good tunings for 23-limit intervals (TE relative error < 5%): 94, 190g, 193, 217, 243e, 270, 282, 311, 328h, 373g, 388, 422, 436, 460, 525, 540, 566g, 581, 624, 639h, 643i, 653, 692i, 718, 742i, 764(h), 814, 860, 882, 908, 935, 954h, 997, 1012, 1046dgh, 1075, 1106, 1125, 1178, 1205g, 1224, 1236(h), 1258, 1282, 1308, 1323, 1357efhi, 1385, 1395, 1419, 1448(g), 1506hi, 1578, 1600, 1646, 1672h, 1677e, 1696, 1718, 1730(g), 1759, 1768gi, 1817hi, 1821ef, 1889, 1920, 1966, 2000, 2038, 2041, 2072, 2087h, 2103, 2113, 2132eh, 2159, 2217, 2231, 2243e, 2270i, 2311, 2320, 2414, 2460 and so on.
- Note: wart notation is used to specify the val chosen for the edo. In the above list, "58hi" means taking the second closest approximations of harmonics 19 and 23.
94edo is the first edo to be consistent in the 23-odd-limit. The smallest edo where the 23-odd-limit is distinctly consistent, meaning each element of the tonality diamond is distinguished, is 282edo, although 311edo may be preferred for excellent consistency in much larger odd limits, and thus is a good choice if you want the 23-odd-limit to be distinctly consistent and the 27-odd-limit (and higher) to be consistent.
23-odd-limit intervals
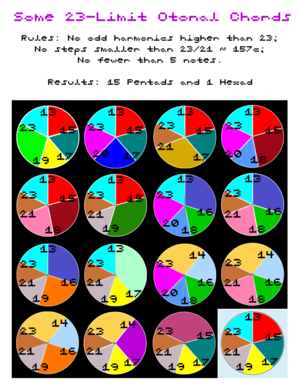
Ratios of 23 in the 23-odd-limit are:
| Ratio | Cents Value | Color Name | Interval Name | |
|---|---|---|---|---|
| 24/23 | 73.681¢ | 23u1 | twethu 1sn | lesser vicesimotertial semitone |
| 23/22 | 76.956¢ | 23o1u2 | twetholu 2nd | greater vicesimotertial semitone |
| 23/21 | 157.493¢ | 23or2 | twethoru 2nd | large vicesimotertial neutral second |
| 26/23 | 212.253¢ | 23u3o2 | twethutho 2nd | vicesimotertial whole tone |
| 23/20 | 241.961¢ | 23og3 | twethogu 3rd | vicesimotertial inframinor third |
| 23/19 | 330.761¢ | 23o19u3 | twethonu 3rd | vicesimotertial supraminor third |
| 28/23 | 340.552¢ | 23uz3 | twethuzo 3rd | vicesimotertial neutral third |
| 23/18 | 424.364¢ | 23o4 | twetho 4th | vicesimotertial diminished fourth |
| 30/23 | 459.994¢ | 23uy3 | twethuyo 3rd | vicesimotertial ultramajor third |
| 23/17 | 523.319¢ | 23o17u4 | twethosu 4th | vicesimotertial acute fourth |
| 32/23 | 571.726¢ | 23u4 | twethu 4th | vicesimotertial narrow tritone |
| 23/16 | 628.274¢ | 23o5 | twetho 5th | vicesimotertial wide tritone |
| 34/23 | 676.681¢ | 23u17o5 | twethuso 5th | vicesimotertial grave fifth |
| 23/15 | 740.006¢ | 23og6 | twethogu 6th | vicesimotertial ultraminor sixth |
| 36/23 | 775.636¢ | 23u5 | twethu 5th | vicesimotertial augmented fifth |
| 23/14 | 859.448¢ | 23or6 | twethoru 6th | vicesimotertial neutral sixth |
| 38/23 | 869.239¢ | 23u19o6 | twethuno 6th | vicesimotertial submajor sixth |
| 40/23 | 958.039¢ | 23uy6 | twethuyo 6th | vicesimotertial ultramajor sixth |
| 23/13 | 987.747¢ | 23o3u7 | twethothu 7th | vicesimotertial minor seventh |
| 42/23 | 1042.507¢ | 23uz7 | twethuzo 7th | small vicesimotertial neutral seventh |
| 44/23 | 1123.044¢ | 23u1o7 | twethulo 7th | vicesimotertial major seventh |
| 23/12 | 1126.391¢ | 23o8 | twetho 8ve | vicesimotertial major seventh |
Trivia
- Unlike most other prime limits, the smallest superparticular ratio of HC23 is larger than the smallest one of HC19. 23 is the first prime limit to show this phenomenon. The ratio is, in fact, larger than the second smallest one of HC19. See List of superparticular intervals.
Music
- Uttuagn (2024)
- Liebestraum No. 3 (1850) – rendered by Randy Wells (2021)
- Siren (Waterhouse) (2021)
- Wilson/Nelson (2021)
- Laudanum (2022)
- Koi Hito (2022)
- Hazybrew (2022)
- Roses and Wolfsbane (2022)
- 2049: A Love Song (2022)
- We're a Midwest Emo Intro Waiting to Happen (2023)
- Phonograph Needle on an Ice Giant's Rings (2023)
- A Cosmic Turtle Grazing Upon Stellar Elements (2023)
- A Hycean World (2023)
- ser0tonin circuits in a neural network (2023)
- Gracias a Dios (2023) for solo jarana (series 23/22, 23/21....23/12)