5L 4s: Difference between revisions
Wikispaces>xenwolf **Imported revision 227758804 - Original comment: links to intervals** |
ArrowHead294 (talk | contribs) mNo edit summary |
||
| (182 intermediate revisions by 18 users not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox MOS}} | |||
{{MOS intro}} It is also equal to a degenerate form of [[diasem]]. | |||
== Names == | |||
The [[TAMNAMS]] convention, used by this article, uses '''semiquartal''' (derived from 'half a fourth') for the 5L 4s pattern. Another attested name is '''hemifourths'''. | |||
== Scale properties == | |||
{{TAMNAMS use}} | |||
& | === Intervals === | ||
{{MOS intervals}} | |||
=== Generator chain === | |||
{{MOS genchain}} | |||
=== Modes === | |||
{{MOS mode degrees}} | |||
Note that the darkest two modes have no diatonic or [[armotonic]] fifth on the root in nonextreme semiquartal tunings. | |||
== Theory == | |||
The harmonic entropy minimum with this MOS pattern is [[godzilla]], in which the generator tempers [[8/7]] or [[7/6]] to be the same interval, and two generators is [[4/3]]. However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament [[semaphore]], there is also a weird scale called "[[pseudo-semaphore]]", in which two different flavors of [[3/2]] exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2. The 2.3.13/5 [[barbados]] temperament is another possible interpretation. | |||
== Tuning ranges == | |||
=== Hard-of-basic === | |||
Hard-of-basic tunings have [[semifourth]]s as generators, between 1\5 (240{{c}}) and 3\14 (257.14{{c}}), where two of them create a diatonic 4th. The generator could be viewed as a 15/13, and the resulting "inframinor" and "ultramajor" chords and triads could be viewed as approximating, respectively, 26:30:39 and 10:13:15 (see [[Arto and tendo theory]]). | |||
==== Hypohard ==== | |||
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard ({{nowrap|2/1 ≤ L/s ≤ 3/1}}) tunings. | |||
{| class="wikitable right-2 right-3 right-4 right-5 right-6" | |||
|- | |||
! | |||
! [[14edo]] ({{nowrap|L/s {{=}} 2/1}}) | |||
! [[47edo]] ({{nowrap|L/s {{=}} 7/3}}) | |||
! [[33edo]] ({{nowrap|L/s {{=}} 5/2}}) | |||
! [[52edo]] ({{nowrap|L/s {{=}} 8/3}}) | |||
! [[19edo]] ({{nowrap|L/s {{=}} 3/1}}) | |||
|- | |||
| Generator (g) | |||
| 3\14, 257.14 | |||
| 10\47, 255.32 | |||
| 7\33, 254.54 | |||
| 11\52, 253.85 | |||
| 4\19, 252.63 | |||
|- | |||
| L ({{nowrap|octave − 4g}}) | |||
| 171.43 | |||
| 178.72 | |||
| 181.81 | |||
| 184.62 | |||
| 189.47 | |||
|- | |||
| s ({{nowrap|5g − octave}}) | |||
| 85.71 | |||
| 76.60 | |||
| 72.73 | |||
| 69.23 | |||
| 63.16 | |||
|} | |||
This range is notable for having many simple tunings that are close to being "eigentunings" (tunings that tune a certain JI interval exactly): | |||
* 33edo semiquartal has close 7/5 (error −0.69{{c}}), 9/5 (error −0.59{{c}}) and 9/7 (error +1.28{{c}}), thus can be used for the close 5:7:9 in the two Locrian-like modes 1|7 and 0|8 | |||
* 52edo semiquartal has close 22/19 (error +0.04{{c}}) | |||
* 19edo semiquartal has close 6/5 (error +0.15{{c}}) and 28/27 (error +0.20{{c}}) | |||
However, for the more complex intervals such as 22/19 and 28/27, you might want to use the exact eigentuning for the full effect, unless you specifically need an edo for modulatory purposes. | |||
==== Parahard and ultrahard ==== | |||
One important sub-range is given by stipulating that two semifourth generators must make a ''meantone'' fourth; i.e. that four fifths should approximate a [[5/4]] major third. This can be considered the [[19edo]] (4\19)-to-[[24edo]] (5\24) range, i.e. parahard semiquartal, which also contains [[43edo]] (9\43) and [[62edo]] (13\62). Parahard semiquartal can be given an RTT interpretation known as [[godzilla]]. | |||
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard ({{nowrap|2/1 ≤ L/s ≤ 3/1}}) tunings. | |||
{| class="wikitable right-2 right-3 right-4 right-5" | |||
|- | |||
! | |||
! [[19edo]] | |||
! [[24edo]] | |||
! [[29edo]] | |||
|- | |||
| Generator (g) | |||
| 4\19, 252.63 | |||
| 5\24, 250.00 | |||
| 6\29, 248.28 | |||
|- | |||
| L ({{nowrap|octave − 4g}}) | |||
| 189.47 | |||
| 200.00 | |||
| 206.90 | |||
|- | |||
| s ({{nowrap|5g − octave}}) | |||
| 63.16 | |||
| 50.00 | |||
| 41.38 | |||
|} | |||
=== Soft-of-basic === | |||
Soft-of-basic tunings have semifourths that are between 3\14 (257.14{{c}}) and 2\9 (266.67{{c}}), creating a "[[mavila]]" or "[[superdiatonic]]" 4th. [[23edo]]'s 5\23 (260.87{{c}}) is an example of this generator. | |||
The sizes of the generator, large step and small step of 5L 4s are as follows in various soft-of-basic tunings. | |||
{| class="wikitable right-2 right-3 right-4 right-5" | |||
|- | |||
! | |||
! [[23edo]] | |||
! [[32edo]] | |||
! [[37edo]] | |||
|- | |||
| Generator (g) | |||
| 5\23, 260.87 | |||
| 7\32, 262.50 | |||
| 8\37, 259.46 | |||
|- | |||
| L ({{nowrap|octave − 4g}}) | |||
| 156.52 | |||
| 150.00 | |||
| 162.16 | |||
|- | |||
| s ({{nowrap|5g − octave}}) | |||
| 104.35 | |||
| 112.50 | |||
| 97.30 | |||
|} | |||
=== Tuning examples === | |||
An example in the Diasem Lydian mode LSLSLMLSLM with M and S equated. ([[:File:Diasem Lydian Example Score.pdf|score]]) | |||
[[File:Diasem Lydian Example 14edo.mp3]] [[14edo]], [[basic]] semiquartal | |||
[[File:Diasem Lydian Example 19edo.mp3]] [[19edo]], [[hard]] semiquartal | |||
[[File:Diasem Lydian Example 23edo.mp3]] [[23edo]], [[soft]] semiquartal | |||
[[File:Diasem Lydian Example 24edo.mp3]] [[24edo]], [[superhard]] semiquartal | |||
[[File:Diasem Lydian Example 33edo semiquartal.mp3]] [[33edo]], [[semihard]] semiquartal | |||
== Scale tree == | |||
{{MOS tuning spectrum | |||
| 5/4 = Septimin | |||
| 4/3 = Beep | |||
| 3/2 = Bug | |||
| 13/8 = Golden bug | |||
| 13/5 = Golden semaphore | |||
| 3/1 = Godzilla | |||
| 11/3 = Semaphore | |||
}} | |||
== Gallery == | |||
[[File:Hemifourths.png|thumb|An alternative diagram with branch depth = 5|alt=|none|507x507px]] | |||
A voice-leading sketch in [[24edo]] by [[Jacob Barton]]: | |||
[[File:qt_mode_chord_prog.mp3|qt mode chord prog]] | |||
== Music == | |||
* [https://www.soundclick.com/bands/songInfo.cfm?bandID=376205&songID=5327098 ''Entropy, the Grandfather of Wind''] (broken link. 2011-03-04) In [[14edo]]{{dead link}} | |||
; [[Frédéric Gagné]] | |||
* ''Whalectric'' (2022) – [https://youtu.be/_E6qvbJWYY8 YouTube] | [https://musescore.com/fredg999/whalectric score] – In [[51edo]], 4|4 mode | |||
; [[Inthar]] | |||
* [[:File:Dream EP 14edo Sketch.mp3|''Dream EP 14edo Sketch'']] (2021) – A short swing ditty in [[14edo]], in the 212121221 mode | |||
* [[:File:19edo Semaphore Fugue.mp3|''19edo Semaphore Fugue'']] (2021) – An unfinished fugue in [[19edo]], in the 212121221 mode | |||
; [[Starshine]] | |||
* [https://soundcloud.com/starshine99/rins-ufo-ride ''Rin's UFO Ride''] (2020) – Semaphore[9] in [[19edo]] | |||
; [[Sevish]] | |||
* [http://www.youtube.com/watch?v=Gcgawrr2xao ''Desert Island Rain''] – Semaphore[9] in [[313edo]] using 65\313 as the generator | |||
[[Category:Semiquartal| ]] <!-- Main article --> | |||
Latest revision as of 13:56, 18 March 2025
| ↖ 4L 3s | ↑ 5L 3s | 6L 3s ↗ |
| ← 4L 4s | 5L 4s | 6L 4s → |
| ↙ 4L 5s | ↓ 5L 5s | 6L 5s ↘ |
┌╥╥┬╥┬╥┬╥┬┐ │║║│║│║│║││ │││││││││││ └┴┴┴┴┴┴┴┴┴┘
sLsLsLsLL
5L 4s, named semiquartal in TAMNAMS, is a 2/1-equivalent (octave-equivalent) moment of symmetry scale containing 5 large steps and 4 small steps, repeating every octave. Generators that produce this scale range from 933.3 ¢ to 960 ¢, or from 240 ¢ to 266.7 ¢. It is also equal to a degenerate form of diasem.
Names
The TAMNAMS convention, used by this article, uses semiquartal (derived from 'half a fourth') for the 5L 4s pattern. Another attested name is hemifourths.
Scale properties
- This article uses TAMNAMS conventions for the names of this scale's intervals and scale degrees. The use of 1-indexed ordinal names is reserved for interval regions.
Intervals
| Intervals | Steps subtended |
Range in cents | ||
|---|---|---|---|---|
| Generic | Specific | Abbrev. | ||
| 0-cthonstep | Perfect 0-cthonstep | P0cts | 0 | 0.0 ¢ |
| 1-cthonstep | Minor 1-cthonstep | m1cts | s | 0.0 ¢ to 133.3 ¢ |
| Major 1-cthonstep | M1cts | L | 133.3 ¢ to 240.0 ¢ | |
| 2-cthonstep | Perfect 2-cthonstep | P2cts | L + s | 240.0 ¢ to 266.7 ¢ |
| Augmented 2-cthonstep | A2cts | 2L | 266.7 ¢ to 480.0 ¢ | |
| 3-cthonstep | Minor 3-cthonstep | m3cts | L + 2s | 240.0 ¢ to 400.0 ¢ |
| Major 3-cthonstep | M3cts | 2L + s | 400.0 ¢ to 480.0 ¢ | |
| 4-cthonstep | Minor 4-cthonstep | m4cts | 2L + 2s | 480.0 ¢ to 533.3 ¢ |
| Major 4-cthonstep | M4cts | 3L + s | 533.3 ¢ to 720.0 ¢ | |
| 5-cthonstep | Minor 5-cthonstep | m5cts | 2L + 3s | 480.0 ¢ to 666.7 ¢ |
| Major 5-cthonstep | M5cts | 3L + 2s | 666.7 ¢ to 720.0 ¢ | |
| 6-cthonstep | Minor 6-cthonstep | m6cts | 3L + 3s | 720.0 ¢ to 800.0 ¢ |
| Major 6-cthonstep | M6cts | 4L + 2s | 800.0 ¢ to 960.0 ¢ | |
| 7-cthonstep | Diminished 7-cthonstep | d7cts | 3L + 4s | 720.0 ¢ to 933.3 ¢ |
| Perfect 7-cthonstep | P7cts | 4L + 3s | 933.3 ¢ to 960.0 ¢ | |
| 8-cthonstep | Minor 8-cthonstep | m8cts | 4L + 4s | 960.0 ¢ to 1066.7 ¢ |
| Major 8-cthonstep | M8cts | 5L + 3s | 1066.7 ¢ to 1200.0 ¢ | |
| 9-cthonstep | Perfect 9-cthonstep | P9cts | 5L + 4s | 1200.0 ¢ |
Generator chain
| Bright gens | Scale degree | Abbrev. |
|---|---|---|
| 13 | Augmented 1-cthondegree | A1ctd |
| 12 | Augmented 3-cthondegree | A3ctd |
| 11 | Augmented 5-cthondegree | A5ctd |
| 10 | Augmented 7-cthondegree | A7ctd |
| 9 | Augmented 0-cthondegree | A0ctd |
| 8 | Augmented 2-cthondegree | A2ctd |
| 7 | Major 4-cthondegree | M4ctd |
| 6 | Major 6-cthondegree | M6ctd |
| 5 | Major 8-cthondegree | M8ctd |
| 4 | Major 1-cthondegree | M1ctd |
| 3 | Major 3-cthondegree | M3ctd |
| 2 | Major 5-cthondegree | M5ctd |
| 1 | Perfect 7-cthondegree | P7ctd |
| 0 | Perfect 0-cthondegree Perfect 9-cthondegree |
P0ctd P9ctd |
| −1 | Perfect 2-cthondegree | P2ctd |
| −2 | Minor 4-cthondegree | m4ctd |
| −3 | Minor 6-cthondegree | m6ctd |
| −4 | Minor 8-cthondegree | m8ctd |
| −5 | Minor 1-cthondegree | m1ctd |
| −6 | Minor 3-cthondegree | m3ctd |
| −7 | Minor 5-cthondegree | m5ctd |
| −8 | Diminished 7-cthondegree | d7ctd |
| −9 | Diminished 9-cthondegree | d9ctd |
| −10 | Diminished 2-cthondegree | d2ctd |
| −11 | Diminished 4-cthondegree | d4ctd |
| −12 | Diminished 6-cthondegree | d6ctd |
| −13 | Diminished 8-cthondegree | d8ctd |
Modes
| UDP | Cyclic order |
Step pattern |
Scale degree (cthondegree) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| 8|0 | 1 | LLsLsLsLs | Perf. | Maj. | Aug. | Maj. | Maj. | Maj. | Maj. | Perf. | Maj. | Perf. |
| 7|1 | 8 | LsLLsLsLs | Perf. | Maj. | Perf. | Maj. | Maj. | Maj. | Maj. | Perf. | Maj. | Perf. |
| 6|2 | 6 | LsLsLLsLs | Perf. | Maj. | Perf. | Maj. | Min. | Maj. | Maj. | Perf. | Maj. | Perf. |
| 5|3 | 4 | LsLsLsLLs | Perf. | Maj. | Perf. | Maj. | Min. | Maj. | Min. | Perf. | Maj. | Perf. |
| 4|4 | 2 | LsLsLsLsL | Perf. | Maj. | Perf. | Maj. | Min. | Maj. | Min. | Perf. | Min. | Perf. |
| 3|5 | 9 | sLLsLsLsL | Perf. | Min. | Perf. | Maj. | Min. | Maj. | Min. | Perf. | Min. | Perf. |
| 2|6 | 7 | sLsLLsLsL | Perf. | Min. | Perf. | Min. | Min. | Maj. | Min. | Perf. | Min. | Perf. |
| 1|7 | 5 | sLsLsLLsL | Perf. | Min. | Perf. | Min. | Min. | Min. | Min. | Perf. | Min. | Perf. |
| 0|8 | 3 | sLsLsLsLL | Perf. | Min. | Perf. | Min. | Min. | Min. | Min. | Dim. | Min. | Perf. |
Note that the darkest two modes have no diatonic or armotonic fifth on the root in nonextreme semiquartal tunings.
Theory
The harmonic entropy minimum with this MOS pattern is godzilla, in which the generator tempers 8/7 or 7/6 to be the same interval, and two generators is 4/3. However, in addition to godzilla (tempering out 81/80) and the 2.3.7 temperament semaphore, there is also a weird scale called "pseudo-semaphore", in which two different flavors of 3/2 exist in the same scale: an octave minus two generators makes a sharp 3/2, and two octaves minus seven generators makes a flat 3/2. The 2.3.13/5 barbados temperament is another possible interpretation.
Tuning ranges
Hard-of-basic
Hard-of-basic tunings have semifourths as generators, between 1\5 (240 ¢) and 3\14 (257.14 ¢), where two of them create a diatonic 4th. The generator could be viewed as a 15/13, and the resulting "inframinor" and "ultramajor" chords and triads could be viewed as approximating, respectively, 26:30:39 and 10:13:15 (see Arto and tendo theory).
Hypohard
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard (2/1 ≤ L/s ≤ 3/1) tunings.
| 14edo (L/s = 2/1) | 47edo (L/s = 7/3) | 33edo (L/s = 5/2) | 52edo (L/s = 8/3) | 19edo (L/s = 3/1) | |
|---|---|---|---|---|---|
| Generator (g) | 3\14, 257.14 | 10\47, 255.32 | 7\33, 254.54 | 11\52, 253.85 | 4\19, 252.63 |
| L (octave − 4g) | 171.43 | 178.72 | 181.81 | 184.62 | 189.47 |
| s (5g − octave) | 85.71 | 76.60 | 72.73 | 69.23 | 63.16 |
This range is notable for having many simple tunings that are close to being "eigentunings" (tunings that tune a certain JI interval exactly):
- 33edo semiquartal has close 7/5 (error −0.69 ¢), 9/5 (error −0.59 ¢) and 9/7 (error +1.28 ¢), thus can be used for the close 5:7:9 in the two Locrian-like modes 1|7 and 0|8
- 52edo semiquartal has close 22/19 (error +0.04 ¢)
- 19edo semiquartal has close 6/5 (error +0.15 ¢) and 28/27 (error +0.20 ¢)
However, for the more complex intervals such as 22/19 and 28/27, you might want to use the exact eigentuning for the full effect, unless you specifically need an edo for modulatory purposes.
Parahard and ultrahard
One important sub-range is given by stipulating that two semifourth generators must make a meantone fourth; i.e. that four fifths should approximate a 5/4 major third. This can be considered the 19edo (4\19)-to-24edo (5\24) range, i.e. parahard semiquartal, which also contains 43edo (9\43) and 62edo (13\62). Parahard semiquartal can be given an RTT interpretation known as godzilla.
The sizes of the generator, large step and small step of 5L 4s are as follows in various hypohard (2/1 ≤ L/s ≤ 3/1) tunings.
| 19edo | 24edo | 29edo | |
|---|---|---|---|
| Generator (g) | 4\19, 252.63 | 5\24, 250.00 | 6\29, 248.28 |
| L (octave − 4g) | 189.47 | 200.00 | 206.90 |
| s (5g − octave) | 63.16 | 50.00 | 41.38 |
Soft-of-basic
Soft-of-basic tunings have semifourths that are between 3\14 (257.14 ¢) and 2\9 (266.67 ¢), creating a "mavila" or "superdiatonic" 4th. 23edo's 5\23 (260.87 ¢) is an example of this generator.
The sizes of the generator, large step and small step of 5L 4s are as follows in various soft-of-basic tunings.
| 23edo | 32edo | 37edo | |
|---|---|---|---|
| Generator (g) | 5\23, 260.87 | 7\32, 262.50 | 8\37, 259.46 |
| L (octave − 4g) | 156.52 | 150.00 | 162.16 |
| s (5g − octave) | 104.35 | 112.50 | 97.30 |
Tuning examples
An example in the Diasem Lydian mode LSLSLMLSLM with M and S equated. (score)
Scale tree
| Generator(edo) | Cents | Step ratio | Comments | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bright | Dark | L:s | Hardness | |||||||
| 7\9 | 933.333 | 266.667 | 1:1 | 1.000 | Equalized 5L 4s | |||||
| 39\50 | 936.000 | 264.000 | 6:5 | 1.200 | ||||||
| 32\41 | 936.585 | 263.415 | 5:4 | 1.250 | Septimin | |||||
| 57\73 | 936.986 | 263.014 | 9:7 | 1.286 | ||||||
| 25\32 | 937.500 | 262.500 | 4:3 | 1.333 | Supersoft 5L 4s Beep | |||||
| 68\87 | 937.931 | 262.069 | 11:8 | 1.375 | ||||||
| 43\55 | 938.182 | 261.818 | 7:5 | 1.400 | ||||||
| 61\78 | 938.462 | 261.538 | 10:7 | 1.429 | ||||||
| 18\23 | 939.130 | 260.870 | 3:2 | 1.500 | Soft 5L 4s Bug | |||||
| 65\83 | 939.759 | 260.241 | 11:7 | 1.571 | ||||||
| 47\60 | 940.000 | 260.000 | 8:5 | 1.600 | ||||||
| 76\97 | 940.206 | 259.794 | 13:8 | 1.625 | Golden bug | |||||
| 29\37 | 940.541 | 259.459 | 5:3 | 1.667 | Semisoft 5L 4s | |||||
| 69\88 | 940.909 | 259.091 | 12:7 | 1.714 | ||||||
| 40\51 | 941.176 | 258.824 | 7:4 | 1.750 | ||||||
| 51\65 | 941.538 | 258.462 | 9:5 | 1.800 | ||||||
| 11\14 | 942.857 | 257.143 | 2:1 | 2.000 | Basic 5L 4s Scales with tunings softer than this are proper | |||||
| 48\61 | 944.262 | 255.738 | 9:4 | 2.250 | ||||||
| 37\47 | 944.681 | 255.319 | 7:3 | 2.333 | ||||||
| 63\80 | 945.000 | 255.000 | 12:5 | 2.400 | ||||||
| 26\33 | 945.455 | 254.545 | 5:2 | 2.500 | Semihard 5L 4s | |||||
| 67\85 | 945.882 | 254.118 | 13:5 | 2.600 | Golden semaphore | |||||
| 41\52 | 946.154 | 253.846 | 8:3 | 2.667 | ||||||
| 56\71 | 946.479 | 253.521 | 11:4 | 2.750 | ||||||
| 15\19 | 947.368 | 252.632 | 3:1 | 3.000 | Hard 5L 4s Godzilla | |||||
| 49\62 | 948.387 | 251.613 | 10:3 | 3.333 | ||||||
| 34\43 | 948.837 | 251.163 | 7:2 | 3.500 | ||||||
| 53\67 | 949.254 | 250.746 | 11:3 | 3.667 | Semaphore | |||||
| 19\24 | 950.000 | 250.000 | 4:1 | 4.000 | Superhard 5L 4s | |||||
| 42\53 | 950.943 | 249.057 | 9:2 | 4.500 | ||||||
| 23\29 | 951.724 | 248.276 | 5:1 | 5.000 | ||||||
| 27\34 | 952.941 | 247.059 | 6:1 | 6.000 | ||||||
| 4\5 | 960.000 | 240.000 | 1:0 | → ∞ | Collapsed 5L 4s | |||||
Gallery
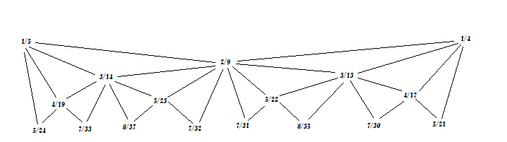
A voice-leading sketch in 24edo by Jacob Barton:
Music
- Entropy, the Grandfather of Wind (broken link. 2011-03-04) In 14edo[dead link]
- Dream EP 14edo Sketch (2021) – A short swing ditty in 14edo, in the 212121221 mode
- 19edo Semaphore Fugue (2021) – An unfinished fugue in 19edo, in the 212121221 mode
- Rin's UFO Ride (2020) – Semaphore[9] in 19edo
- Desert Island Rain – Semaphore[9] in 313edo using 65\313 as the generator