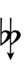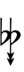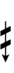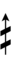37edo
| ← 36edo | 37edo | 38edo → |
37 equal divisions of the octave (abbreviated 37edo or 37ed2), also called 37-tone equal temperament (37tet) or 37 equal temperament (37et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 37 equal parts of about 32.4 ¢ each. Each step represents a frequency ratio of 21/37, or the 37th root of 2.
Theory
37edo has very accurate approximations of harmonics 5, 7, 11 and 13, making it a good choice for a no-threes approach. Harmonic 11 is particularly accurate, being only 0.03 cents sharp.
Using its best (and sharp) fifth, 37edo tempers out 250/243, making it a variant of porcupine temperament. It is the optimal patent val for porcupinefish, which is about as accurate as 13-limit porcupine extensions will be. Using its alternative flat fifth, it tempers out 16875/16384, making it a negri tuning. It also tempers out 2187/2000, resulting in a temperament where three minor whole tones make up a fifth (gorgo/laconic).
37edo is also a very accurate equal tuning for undecimation temperament, which has a generator of about 519 cents; 2 generators lead to 29/16; 3 generators to 32/13; 6 generators to a 10 cent sharp 6/1; 8 generators to a very accurate 11/1 and 10 generators to 20/1. It has a 7L 2s enneatonic mos, which in 37edo scale degrees is 0, 1, 6, 11, 16, 17, 22, 27, 32, a scale structure reminiscent of mavila; as well as a 16-note mos.
In the no-3 13-odd-limit, 37edo maintains the smallest relative error of any edo until 851edo, and the smallest absolute error until 103edo[clarification needed].
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +11.6 | +2.9 | +4.1 | -9.3 | +0.0 | +2.7 | +14.4 | -7.7 | -5.6 | +15.7 | -12.1 |
| Relative (%) | +35.6 | +8.9 | +12.8 | -28.7 | +0.1 | +8.4 | +44.5 | -23.6 | -17.3 | +48.4 | -37.2 | |
| Steps (reduced) |
59 (22) |
86 (12) |
104 (30) |
117 (6) |
128 (17) |
137 (26) |
145 (34) |
151 (3) |
157 (9) |
163 (15) |
167 (19) | |
Subsets and supersets
37edo is the 12th prime edo, following 31edo and coming before 41edo.
74edo, which doubles it, provides an alternative approximation to harmonic 3 that supports meantone. 111edo, which triples it, gives a very accurate approximation of harmonic 3, and manifests itself as a great higher-limit system. 296edo, which slices its step in eight, is a good 13-limit system.
Subgroups
37edo offers close approximations to harmonics 5, 7, 11, and 13, and a usable approximation of 9 as well.
- 12\37 = 389.2 cents
- 30\37 = 973.0 cents
- 17\37 = 551.4 cents
- 26\37 = 843.2 cents
- [6\37 = 194.6 cents]
This means 37 is quite accurate on the 2.5.7.11.13 subgroup, where it shares the same tuning as 111edo. In fact, on the larger 3*37 subgroup 2.27.5.7.11.13.51.57 subgroup not only shares the same tuning as 19-limit 111edo, it tempers out the same commas. A simpler but less accurate approach is to use the 2*37-subgroup, 2.9.7.11.13.17.19, on which it has the same tuning and commas as 74edo.
Dual fifths
The just perfect fifth of frequency ratio 3:2 is not well-approximated, and falls between two intervals in 37edo:
The flat fifth is 21\37 = 681.1 cents (37b val)
The sharp fifth is 22\37 = 713.5 cents
21\37 generates an anti-diatonic, or mavila, scale: 5 5 6 5 5 5 6
"minor third" = 10\37 = 324.3 cents
"major third" = 11\37 = 356.8 cents
22\37 generates an extreme superpythagorean scale: 7 7 1 7 7 7 1
"minor third" = 8\37 = 259.5 cents
"major third" = 14\37 = 454.1 cents
If the minor third of 259.5 cents is mapped to 7/6, this superpythagorean scale can be thought of as a variant of Oceanfront temperament.
37edo can only barely be considered as "dual-fifth", because the sharp fifth is 12 cents sharp of 3/2, has a regular diatonic scale, and can be interpreted as somewhat accurate regular temperaments like archy and the aforementioned oceanfront. In contrast, the flat fifth is 21 cents flat and the only low-limit interpretation is as the very inaccurate mavila.
Since both fifths do not support meantone, the "major thirds" of both systems are not 12\37 = 389.2¢, the closest approximation to 5/4 available in 37edo.
37edo has great potential as a near-just xenharmonic system, with high-prime chords such as 8:10:11:13:14 with no perfect fifths available for common terrestrial progressions. The 9/8 approximation is usable but introduces error. One may choose to treat either of the intervals close to 3/2 as 3/2, introducing additional approximations with considerable error (see interval table below).
No-3 approach
If prime 3 is ignored, 37edo represents the no-3 23-odd-limit consistently, and is distinctly consistent within the no-3 16-integer-limit.
Intervals
| Degrees | Cents | Approximate Ratios of 2.5.7.11.13.27 subgroup |
Additional Ratios of 3 with a sharp 3/2 |
Additional Ratios of 3 with a flat 3/2 |
Additional Ratios of 9 with 194.59¢ 9/8 |
|---|---|---|---|---|---|
| 0 | 0.00 | 1/1 | |||
| 1 | 32.43 | 55/54, 56/55 | |||
| 2 | 64.86 | 27/26, 28/27 | |||
| 3 | 97.30 | 128/121, 55/52 | 16/15 | ||
| 4 | 129.73 | 14/13 | 13/12, 15/14 | 12/11 | |
| 5 | 162.16 | 11/10 | 10/9, 12/11 | 13/12 | |
| 6 | 194.59 | 28/25 | 9/8, 10/9 | ||
| 7 | 227.03 | 8/7 | 9/8 | ||
| 8 | 259.46 | 7/6, 15/13 | |||
| 9 | 291.89 | 13/11, 32/27 | 6/5, 7/6 | ||
| 10 | 324.32 | 6/5, 11/9 | |||
| 11 | 356.76 | 16/13, 27/22 | 11/9 | ||
| 12 | 389.19 | 5/4 | |||
| 13 | 421.62 | 14/11, 32/25 | 9/7 | ||
| 14 | 454.05 | 13/10 | 9/7 | ||
| 15 | 486.49 | 4/3 | |||
| 16 | 518.92 | 27/20 | 4/3 | ||
| 17 | 551.35 | 11/8 | 15/11 | 18/13 | |
| 18 | 583.78 | 7/5 | 18/13 | ||
| 19 | 616.22 | 10/7 | 13/9 | ||
| 20 | 648.65 | 16/11 | 22/15 | 13/9 | |
| 21 | 681.08 | 40/27 | 3/2 | ||
| 22 | 713.51 | 3/2 | |||
| 23 | 745.95 | 20/13 | 14/9 | ||
| 24 | 778.38 | 11/7, 25/16 | 14/9 | ||
| 25 | 810.81 | 8/5 | |||
| 26 | 843.24 | 13/8, 44/27 | 18/11 | ||
| 27 | 875.68 | 5/3, 18/11 | |||
| 28 | 908.11 | 22/13, 27/16 | 5/3, 12/7 | ||
| 29 | 940.54 | 12/7, 26/15 | |||
| 30 | 972.97 | 7/4 | 16/9 | ||
| 31 | 1005.41 | 25/14 | 16/9, 9/5 | ||
| 32 | 1037.84 | 20/11 | 9/5, 11/6 | ||
| 33 | 1070.27 | 13/7 | 24/13, 28/15 | 11/6 | |
| 34 | 1102.70 | 121/64, 104/55 | 15/8 | ||
| 35 | 1135.14 | 27/14, 52/27 | |||
| 36 | 1167.57 | ||||
| 37 | 1200.00 | 2/1 |
Notation
Ups and downs notation
37edo can be notated using ups and downs notation:
| Degrees | Cents | Ups and downs notation | ||
|---|---|---|---|---|
| 0 | 0.00 | Perfect 1sn | P1 | D |
| 1 | 32.43 | Minor 2nd | m2 | Eb |
| 2 | 64.86 | Upminor 2nd | ^m2 | ^Eb |
| 3 | 97.30 | Downmid 2nd | v~2 | ^^Eb |
| 4 | 129.73 | Mid 2nd | ~2 | Ed |
| 5 | 162.16 | Upmid 2nd | ^~2 | vvE |
| 6 | 194.59 | Downmajor 2nd | vM2 | vE |
| 7 | 227.03 | Major 2nd | M2 | E |
| 8 | 259.46 | Minor 3rd | m3 | F |
| 9 | 291.89 | Upminor 3rd | ^m3 | ^F |
| 10 | 324.32 | Downmid 3rd | v~3 | ^^F |
| 11 | 356.76 | Mid 3rd | ~3 | Ft |
| 12 | 389.19 | Upmid 3rd | ^~3 | vvF# |
| 13 | 421.62 | Downmajor 3rd | vM3 | vF# |
| 14 | 454.05 | Major 3rd | M3 | F# |
| 15 | 486.49 | Perfect 4th | P4 | G |
| 16 | 518.92 | Up 4th, Dim 5th | ^4, d5 | ^G, Ab |
| 17 | 551.35 | Downmid 4th, Updim 5th | v~4, ^d5 | ^^G, ^Ab |
| 18 | 583.78 | Mid 4th, Downmid 5th | ~4, v~5 | Gt, ^^Ab |
| 19 | 616.22 | Mid 5th, Upmid 4th | ~5, ^~4 | Ad, vvG# |
| 20 | 648.65 | Upmid 5th, Downaug 5th | ^~5, vA4 | vvA, vG# |
| 21 | 681.08 | Down 5th, Aug 4th | v5, A4 | vA, G# |
| 22 | 713.51 | Perfect 5th | P5 | A |
| 23 | 745.95 | Minor 6th | m6 | Bb |
| 24 | 778.38 | Upminor 6th | ^m6 | ^Bb |
| 25 | 810.81 | Downmid 6th | v~6 | ^^Bb |
| 26 | 843.24 | Mid 6th | ~6 | Bd |
| 27 | 875.68 | Upmid 6th | ^~6 | vvB |
| 28 | 908.11 | Downmajor 6th | vM6 | vB |
| 29 | 940.54 | Major 6th | M6 | B |
| 30 | 972.97 | Minor 7th | m7 | C |
| 31 | 1005.41 | Upminor 7th | ^m7 | ^C |
| 32 | 1037.84 | Downmid 7th | v~7 | ^^C |
| 33 | 1070.27 | Mid 7th | ~7 | Ct |
| 34 | 1102.70 | Upmid 7th | ^~7 | vvC# |
| 35 | 1135.14 | Downmajor 7th | vM7 | vC# |
| 36 | 1167.57 | Major 7th | M7 | C# |
| 37 | 1200.00 | Perfect 8ve | P8 | D |
37edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Half-sharps and half-flats can be used to avoid triple arrows:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Alternative ups and downs have sharps and flats with arrows borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
Ivan Wyschnegradsky's notation
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
Sagittal notation
This notation uses the same sagittal sequence as EDOs 23b, 30, and 44.
Evo and Revo flavors

Alternative Evo flavor

Evo-SZ flavor

Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.5 | [86 -37⟩ | [⟨37 86]] | −0.619 | 0.619 | 1.91 |
| 2.5.7 | 3136/3125, 4194304/4117715 | [⟨37 86 104]] | −0.905 | 0.647 | 2.00 |
| 2.5.7.11 | 176/175, 1375/1372, 65536/65219 | [⟨37 86 104 128]] | −0.681 | 0.681 | 2.10 |
| 2.5.7.11.13 | 176/175, 640/637, 847/845, 1375/1372 | [⟨37 86 104 128 137]] | −0.692 | 0.610 | 1.88 |
- 37et is most prominent in the no-3 11-, 13-, 17-, 19- and 23-limit subgroups. The next equal temperaments doing better in these subgroups are 109, 581, 103, 124 and 93, respectively.
Rank-2 temperaments
| Generator | In patent val | In 37b val |
|---|---|---|
| 1\37 | ||
| 2\37 | Sycamore | |
| 3\37 | Passion | |
| 4\37 | Twothirdtonic | Negri |
| 5\37 | Porcupine / porcupinefish | |
| 6\37 | Didacus / roulette | |
| 7\37 | Shoe / semaja | Shoe / laconic / gorgo |
| 8\37 | Semaphore (37bd) | |
| 9\37 | Gariberttet | |
| 10\37 | Orgone | |
| 11\37 | Beatles | |
| 12\37 | Würschmidt (out-of-tune) | |
| 13\37 | Skwares (37dd) | |
| 14\37 | Ammonite | |
| 15\37 | Ultrapyth, oceanfront | |
| 16\37 | Undecimation | |
| 17\37 | Freivald, emka, onzonic | |
| 18\37 | ||
Scales
Every 8 steps of 37edo
| Degrees | Cents | Approximate Ratios of 6.7.11.20.27 subgroup |
Additional Ratios |
|---|---|---|---|
| 0 | 0.000 | 1/1 | |
| 1 | 259.46 | 7/6 | |
| 2 | 518.92 | 27/20 | |
| 3 | 778.38 | 11/7 | |
| 4 | 1037.84 | 20/11, 11/6 | |
| 5 | 1297.30 | 19/9 | |
| 6 | 1556.76 | 27/11 | |
| 7 | 1816.22 | 20/7 | |
| 8 | 2075.68 | 10/3 | |
| 9 | 2335.14 | 27/7 | |
| 10 | 2594.59 | 9/2 | |
| 11 | 2854.05 | 26/5 | |
| 12 | 3113.51 | 6/1 | |
| 13 | 3372.97 | 7/1 | |
| 14 | 3632.43 | ||
| 15 | 3891.89 | 19/2 | |
| 16 | 4151.35 | 11/1 | |
| 17 | 4410.81 | ||
| 18 | 4670.27 | ||
| 19 | 4929.73 | ||
| 20 | 5189.19 | 20/1 | |
| 21 | 5448.65 | ||
| 22 | 5708.11 | 27/1 |
Instruments
- Lumatone
- Fretted instruments
Music
- Mindless vibe (2023)
- 5 days in (2023)
- A Dark Era Arises (2023) – in Porcupine[15], 37edo tuning
- Two Faced People (2025) – in Twothirdtonic[10], 37edo tuning
- "Shorn Brown" from Newbeams (2012)
- "Jellybear" from Newbeams (2012)
- Tyrian and Gold (2024)
- Bittersweet End (2025)
- What if? (2023)
- Deck The Halls (2022)
- Marcello - Bach: Adagio from BWV 974, arranged for Oboe & Organ, tuned into 37edo (2022)
- Little Fugue on Happy Birthday (2022) – in Passion, 37edo tuning
- Fugue on an Original Theme (2022)
- Paradies, Toccata, Arranged for Organ and Tuned into 37edo (2023)
- No.27.50 (2022)
- Luck of the Draw (2023)
- The Kog Sisters (2014)
- Afrikan Song (2016)
- Porcupine Lullaby (2020) – in Porcupine, 37edo tuning
- Fugue for Brass in 37EDO sssLsss "Dingoian" (2022) – in Porcupine[7], 37edo tuning
- Fugue for Klezmer Band in 37EDO Porcupine[7] sssssLs "Lemurian" (2023) – in Porcupine[7], 37edo tuning
- Elevated Floors (2025)
- cat jam 37 (2025)
- Winter (2025)
- XENO*n*
- Galantean Drift (2025)