5edo

← 4edo

5edo

6edo →

Prime factorization	5 (prime)
Step size	240 ¢
Fifth	3\5 (720 ¢) (convergent)
Semitones (A1:m2)	1:0 (240 ¢ : 0 ¢)
Consistency limit	9
Distinct consistency limit	3
Special properties	Zeta peak Zeta peak integer Zeta integral Zeta gap

5 equal divisions of the octave (abbreviated 5edo or 5ed2), also called 5-tone equal temperament (5tet) or 5 equal temperament (5et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 5 equal parts of exactly 240 ¢ each. Each step represents a frequency ratio of 2^1/5, or the 5th root of 2.

5edo is notable for being the smallest edo containing xenharmonic intervals—1edo, 2edo, 3edo, and 4edo are all subsets of 12edo.

Theory

A chromatic 5edo scale on C.

5edo is the basic example of an equipentatonic scale, containing a sharp but usable perfect fifth, and can be seen as a simplified form of the familiar pentic scale. Tertian harmony is possible in 5edo, but barely: the only chords available are suspended chords, which may also be seen as inframinor (very flat minor) and ultramajor (very sharp major) chords, due to how sharp the fifth is. As a result, many triads will share the same three notes, so rootedness is much more important to explicitly establish.

In terms of just intonation, 5edo represents the perfect fifth 3/2 and harmonic seventh 7/4 rather accurately for how wide the steps are, with 3 being about 20 cents sharp, and 7 being about 10 cents flat. In 5edo, the perfect fifth is 3 steps, meaning it can be divided into 3 equal parts, each representing the supermajor second 8/7. This is slendric temperament. Two of these parts make the perfect fourth 4/3, which is semaphore temperament, and finally the harmonic seventh may be found by going up two perfect fourths, which is superpyth or "archy" temperament. This all means that 5edo contains a very simplified form of the 2.3.7 subgroup, and many scales in 2.3.7 take a pentatonic form.

With more complex intervals, however, 5edo becomes increasingly inaccurate. For example, the supermajor third 9/7 is the same interval as the perfect fourth, which is a rather inaccurate equivalence (specifically, trienstonic temperament). However, this can still be used as a third, as referenced in the top paragraph.

If we extend our scope to the full 7-limit (including 5, and thus conventional major and minor thirds), then the most salient fact is that the best approximation of the major third 5/4 is extremely inaccurate, almost a full semitone sharper than just. This results in 5edo supporting several exotemperaments when intervals of 5 are introduced. For example, the best 5/4 of 480 cents is in fact the same interval as 4/3, meaning that the semitone that usually separates them, 16/15, is tempered out (which is the very inaccurate father temperament).

Exploring more complex intervals, we find that the minor tone 10/9 and the minor third 6/5 are best mapped to the same step of 240 cents, meaning that the semitone separating them, 27/25, is tempered out as well - this is bug temperament, which is a little more perverse even than father.

Because these intervals are so large, this sort of analysis is less significant with 5edo than it becomes with larger and more accurate divisions, but it still plays a role. For example, if we attempt to analyze 5edo as supporting standard diatonic harmony, I–IV–V–I is the same as I–III–V–I and involves triads with common intervals because of fourth-thirds equivalence.

If 5edo is taken as only a tuning of the 3-limit, we find that the circle of fifths returns to the unison after only 5 steps, rather than 12. This is called blackwood temperament, and in 5edo, this is a "good" tuning of a circle of fifths - more formally, since the comma being tempered out, the semitone 256/243, is smaller than half a step (120 cents), 5edo demonstrates 3-to-2 telicity (and is the third EDO to do so after 1edo and 2edo).

5edo is the smallest edo representing the 9-odd-limit consistently, giving a distinct value modulo 5 to 1, 3, 5, 7 and 9 - specifically, 3 is mapped to 3 steps (720 cents), 5 is very inaccurately mapped to 2 steps (480 cents), 7 is mapped to 4 steps (960 cents), and 9 is mapped to 1 step (240 cents). However, while 2edo represents the 3-odd-limit consistently, 3edo the 5-odd-limit, 4edo the 7-odd-limit and 5edo the 9-odd-limit, to represent the 11-odd-limit consistently with a patent val requires going all the way to 22edo.

Despite its lack of accuracy in the 5-limit, 5edo is the second zeta integral edo, after 2edo.

Prime harmonics

Approximation of prime harmonics in 5edo

Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	Absolute (¢)	+0	+18	+94	-9	-71	+119	-105	-58	+92	-70	+55
	Relative (%)	+0.0	+7.5	+39.0	-3.7	-29.7	+49.8	-43.7	-24.0	+38.2	-29.0	+22.9
Steps (reduced)		5 (0)	8 (3)	12 (2)	14 (4)	17 (2)	19 (4)	20 (0)	21 (1)	23 (3)	24 (4)	25 (0)

Subsets and supersets

5edo is the 3rd prime edo, after 2edo and 3edo and before 7edo. It does not contain any nontrivial subset edos, though it contains 5ed4. Multiples such as 10edo, 15edo, … up to 35edo, share the same tuning of the perfect fifth as 5edo, while improving on other intervals.

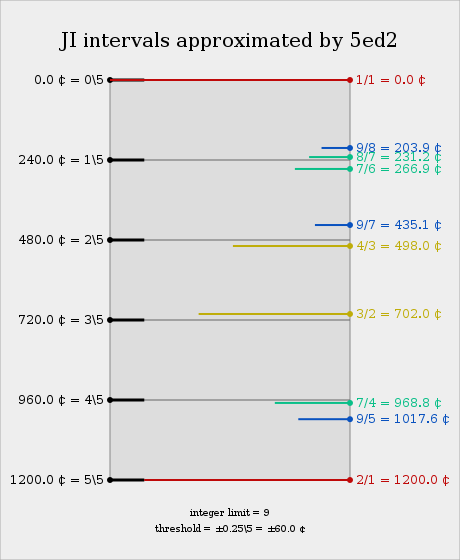
Intervals

Intervals of 5edo

Degree	Cents	Interval region	Approximated JI intervals (error in ¢)				Audio
			3-limit	5-limit	7-limit	Other
0	0	Unison (prime)	1/1 (just)
1	240	Second-inter-third		144/125 (-4.969) 125/108 (-13.076)	8/7 (+8.826) 7/6 (-26.871)	224/195 (-0.030)
2	480	Fourth	4/3 (-18.045)		21/16 (+9.219)	33/25 (-0.686)
3	720	Fifth	3/2 (+18.045)		32/21 (-9.219)	50/33 (+0.686)
4	960	Sixth-inter-seventh		216/125 (+13.076) 125/72 (+4.969)	12/7 (+26.871) 7/4 (-8.826)	195/112 (+0.030)
5	1200	Octave	2/1 (just)

Notation

The usual notation system for 5edo is the heptatonic chain-of-fifths notation, which is directly derived from the standard notation used in 12edo. The enharmonic unison is the minor 2nd, thus E and F are the same pitch.

Notation of 5edo

Degree	Cents	Chain-of-fifths notation
		Diatonic interval names	Note names (on D)
0	0	Perfect unison (P1) Minor second (m2) Diminished third (d3)	D Eb Fb
1	240	Augmented unison (A1) Major second (M2) Minor third (m3) Diminished fourth (d4)	D# E F Gb
2	480	Augmented second (A2) Major third (M3) Perfect fourth (P4) Diminished fifth (d5)	E# F# G Ab
3	720	Augmented fourth (A4) Perfect fifth (P5) Minor sixth (m6) Diminished seventh (d7)	G# A Bb Cb
4	960	Augmented fifth (A5) Major sixth (M6) Minor seventh (m7) Diminished octave (d8)	A# B C Db
5	1200	Augmented sixth (A6) Major seventh (M7) Perfect octave (P8)	B# C# D

In 5edo:

• ups and downs notation is identical to circle-of-fifths notation;
• mixed sagittal notation is identical to circle-of-fifths notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp () and sagittal flat () respectively.

Sagittal notation

This notation uses the same sagittal sequence as EDOs 12, 19, and 26, and is a subset of the notations for EDOs 10, 15, 20, 25, 30, and 35b.

Because it includes no Sagittal symbols, this Sagittal notation is also a conventional notation.

Alternative notations

• via Reinhard's cents notation
• a four-line hybrid treble/bass staff.

Intervals can be named penta-2nd, penta-3rd, penta-4th, penta-5th and hexave. The circle of fifths: 1sn -- penta-4th -- penta-2nd -- penta-5th -- penta-3rd -- 1sn.

Kite Giedraitis has proposed pentatonic interval names that retain the appearance of heptatonic names, to avoid the confusion caused by one's lifelong association of "fourth" with 4/3, not 3/2. The interval names are unisoid, subthird, fourthoid, fifthoid, subseventh and octoid, or 1d s3 4d 5d s7 8d. The circle of fifths: 1d -- 5d -- s3 -- s7 -- 4d -- 1d. When notating larger edos such as 8 or 13 this way, there are major or minor sub3rds and sub7ths. Note that 15/8 is an octoid and 16/15 is a unisoid.

For note names, Kite often omits B and merges E and F into a new letter, "eef" (rhymes with leaf). Eef, like E, is a 5th above A. Eef, like F, is a 4th above C. The circle of 5ths is C G D A Eef C. Eef is written like an E, but with the bottom horizontal line going not right but left from the vertical line. Eef can be typed as ⺘(unicode 2E98 or 624C) or ꘙ (unicode A619) or 𐐆 (unicode 10406). Eef can also be used to notate 15edo.

Solfege

Solfege of 5edo

Degree	Cents	Standard solfege (movable do)	Uniform solfege (1 vowel)
0	0	Do (P1)	Da (P1)
1	240	Re (M2) Me (m3)	Ra (M2) Na (m3)
2	480	Mi (M3) Fa (P4)	Ma (M3) Fa (P4)
3	720	So (P5) Le (m6)	Sa (P5) Fla (m6)
4	960	La (M6) Te (m7)	La (M6) Tha (m7)
5	1200	Ti (M7) Do (P8)	Da (P8)

Approximation to JI

Selected 7-limit intervals

5ed2-001.svg

Zeta peak index

Tuning			Strength				Octave (cents)		Integer limit
ZPI	Steps per 8ve	Step size (cents)	Height		Integral	Gap	Size	Stretch	Consistent	Distinct
			Tempered	Pure
9zpi	5.034476	238.356503	3.664837	3.563852	1.131648	13.386581	1191.782517	−8.217483	10	4

Observations

Related scales

• By its cardinality, 5edo is related to other pentatonic scales, and it is especially close in sound to many Indonesian slendros.
• Due to the interest around the "fifth" interval size, there are many nonoctave "stretch sisters" to 5edo: square root of 4/3, cube root of 3/2, 8th root of 3, etc.
• For the same reason there are many "circle sisters":
  • Make a chain of five "bigger fifths" (50/33), which makes three octaves 3.227¢ flat. (50/33)^5 = 7.985099.

Cycles, divisions

5 is a prime number so 5edo contains no sub-edos. Only simple cycles:

• Cycle of seconds: 0-1-2-3-4-0
• Cycle of fourths: 0-2-4-1-3-0
• Cycle of fifths: 0-3-1-4-2-0
• Cycle of sevenths: 0-4-3-2-1-0

Harmony

5edo does not have any strong consonance nor dissonance. It could be considered omniconsonant. The 240 cent interval can serve as either a major second or minor third, and the 960 cent interval as either a major sixth or minor seventh. The fourth is about 18 cents flat of a just fourth, making it rather "dirty" but recognizable. The fifth is likewise about 18 cents sharp of a just fifth, dissonant but still easily recognizable.

In contrast to other edos, all of the notes can be used at once in order to get a functioning scale. (As in Blackwood in 10edo).

Important chords:

• 0+1+3
• 0+2+3
• 0+1+3+4
• 0+2+3+4

Melody

Smallest edo that can be used for melodies in a "standard" way. The relatively large step of 240 cents can be used as major second for the melody construction. The scale has whole-tone as well as pentatonic character.

Chord or scale?

Either way, it is hard to wander very far from where you start. However, it has the scale-like feature that there are (barely) enough notes to create melody, in the form of an equal version of pentatonic.

Regular temperament properties

Uniform maps

13-limit uniform maps between 4.8 and 5.2

Min. size	Max. size	Wart notation	Map
4.7696	4.8088	5cddf	⟨5 8 11 13 17 18]
4.8088	4.9528	5cf	⟨5 8 11 14 17 18]
4.9528	4.9994	5f	⟨5 8 12 14 17 18]
4.9994	5.0586	5	⟨5 8 12 14 17 19]
5.0586	5.1650	5e	⟨5 8 12 14 18 19]
5.1650	5.2696	5de	⟨5 8 12 15 18 19]

Commas

5et tempers out the following commas. This assumes the val ⟨5 8 12 14 17 19].

Prime limit	Ratio	Monzo	Cents	Color name	Name(s)
3	256/243	[8 -5⟩	90.225	Sawa	Blackwood comma, Pythagorean limma
5	27/25	[0 3 -2⟩	133.238	Gugu	Bug comma, large limma
5	16/15	[4 -1 -1⟩	111.731	Gubi	Dicot comma, classic chroma
5	81/80	[-4 4 -1⟩	21.506	Gu	Syntonic comma, Didymus' comma, meantone comma
5	(22 digits)	[24 -21 4⟩	4.200	Sasa-quadyo	Vulture comma
7	36/35	[2 2 -1 -1⟩	48.770	Rugu	Mint comma, septimal quartertone
7	49/48	[-4 -1 0 2⟩	35.697	Zozo	Semaphoresma, slendro diesis
7	64/63	[6 -2 0 -1⟩	27.264	Ru	Septimal comma, Archytas' comma, Leipziger Komma
7	245/243	[0 -5 1 2⟩	14.191	Zozoyo	Sensamagic comma
7	1728/1715	[6 3 -1 -3⟩	13.074	Triru-agu	Orwellisma
7	1029/1024	[-10 1 0 3⟩	8.433	Latrizo	Gamelisma
7	19683/19600	[-4 9 -2 -2⟩	7.316	Labiruru	Cataharry comma
7	5120/5103	[10 -6 1 -1⟩	5.758	Saruyo	Hemifamity comma
7	(18 digits)	[-26 -1 1 9⟩	3.792	Latritrizo-ayo	Wadisma
7	(12 digits)	[-6 -8 2 5⟩	1.117	Quinzo-ayoyo	Wizma
11	11/10	[-1 0 -1 0 1⟩	165.004	Logu	Large undecimal neutral 2nd
11	99/98	[-1 2 0 -2 1⟩	17.576	Loruru	Mothwellsma
11	896/891	[7 -4 0 1 -1⟩	9.688	Saluzo	Pentacircle comma
11	385/384	[-7 -1 1 1 1⟩	4.503	Lozoyo	Keenanisma
11	441/440	[-3 2 -1 2 -1⟩	3.930	Luzozogu	Werckisma
11	3025/3024	[-4 -3 2 -1 2⟩	0.572	Loloruyoyo	Lehmerisma
13	14/13	[1 0 0 1 0 -1⟩	128.298	Thuzo	Tridecimal 2/3-tone, trienthird
13	91/90	[-1 -2 -1 1 0 1⟩	19.130	Thozogu	Superleap comma, biome comma
13	676/675	[2 -3 -2 0 0 2⟩	2.563	Bithogu	Island comma, parizeksma

Ear training

5edo ear-training exercises by Alex Ness available here:

• https://drive.google.com/folderview?id=0BwsXD8q2VCYUT3VEZUVmeVZUcmc&usp=drive_web

For any musician, there is no substitute for the experience of a particular xenharmonic sound. The user going by the name Hyacinth on Wikipedia and Wikimedia Commons has many xenharmonic MIDI's and has graciously copylefted them! This is his 5-TET scale MIDI:

• http://commons.wikimedia.org/wiki/File:5-tet_scale_on_C.mid

Music

Main article: Music in 5edo

See also: Category:5edo tracks

There is also much 5edo-like world music, just search for "gyil" or "amadinda" or "slendro".