35edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Jkarimak (talk | contribs)
191 edits
m →Intervals: typo
Fredg999 (talk | contribs)
autopatrolled, Interface administrators, Sysops
6,129 edits
m Text replacement - "Ups and Downs Notation" to "Ups and downs notation"
 
(56 intermediate revisions by 22 users not shown)
Line 1: Line 1:
35-tET or 35-[[EDO]] refers to a tuning system which divides the octave into 35 steps of approximately [[cent|34.29¢]] each.
{{Infobox ET}}
{{ED intro}}


As 35 is 5 times 7, 35edo allows for mixing the two smallest xenharmonic [[macrotonal edos]]: [[5edo]] and [[7edo]]. A single degree of 35edo represents the difference between 7edo's narrow fifth of 685.71¢ and 5edo's wide fifth of 720¢. Because it includes 7edo, 35edo tunes the 29th harmonic with +1 cent of error. 35edo can also represent the 2.3.5.7.11.17 [[Just_intonation_subgroups|subgroup]] and 2.9.5.7.11.17 subgroup, because of the accuracy of 9 and the flatness of all other subgroup generators (7/5 and 17/11 stand out, having less than 1 cent error). Therefore among whitewood tunings it is very versatile; you can switch between these different subgroups if you don't mind having to use two different 3/2s to reach the inconsistent 9 (a characteristic of whitewood tunings), and if you ignore [[22edo]]'s more in-tune versions of 35edo MOS's and consistent representation of both subgroups. 35edo has the optimal patent val for [[greenwood]] and [[secund]] temperaments, as well as 11-limit [[muggles]], and the 35f val is an excellent tuning for 13-limit muggles.
== Theory ==
As 35 is 5 times 7, 35edo allows for mixing the two smallest xenharmonic [[macrotonal edos]]: [[5edo]] and [[7edo]]. A single degree of 35edo represents the difference between 7edo's narrow fifth of 685.71{{c}} and 5edo's wide fifth of 720{{c}}. Because it includes 7edo, 35edo tunes the 29th harmonic with only 1{{c}} of error.


=Notation=
35edo can also represent the 2.3.5.7.11.17 [[subgroup]] and 2.9.5.7.11.17 subgroup, because of the accuracy of 9 and the flatness of all other subgroup generators (7/5 and 17/11 stand out, having less than 1 cent error). Therefore among [[whitewood]] tunings it is very versatile; you can switch between these different subgroups if you don't mind having to use two different 3/2s to reach the inconsistent 9 (a characteristic of whitewood tunings), and if you ignore [[22edo]]'s more in-tune versions of 35edo MOS's and consistent representation of both subgroups.


35edo has the optimal [[patent val]] for [[greenwood]] and [[secund]] temperaments, as well as 11-limit [[muggles]], and the 35f val is an excellent tuning for 13-limit muggles. 35edo is the largest edo with a lack of a [[diatonic scale]] (unless 7edo is considered a diatonic scale).
=== Odd harmonics ===
{{Harmonics in equal|35}}
== Notation ==
The 7edo fifth is preferred as the diatonic generator for ups and downs notation due to being much easier to notate than the 5edo fifth (which involves E and F being enharmonic), as well as being closer to 3/2.
{| class="wikitable"
{| class="wikitable"
|-
|-
! style="text-align:center;" | Degrees
! Degrees
! style="text-align:center;" | Cents
! Cents
! colspan="3" style="text-align:center;" | [[Ups_and_Downs_Notation|Up/down]] [[Ups_and_Downs_Notation|Notation]]
! colspan="3" | [[Ups and downs notation]]
! [[Dual-fifth tuning|Dual-fifth]] notation
<small>based on closest 12edo interval</small>
|-
|-
| style="text-align:center;" | 0
| 0
| style="text-align:center;" | 0.000
| 0.000
| style="text-align:center;" | unison
| unison
| style="text-align:center;" | 1
| 1
| style="text-align:center;" | D
| D
| 1sn, prime
|-
|-
| style="text-align:center;" | 1
| 1
| style="text-align:center;" | 34.286
| 34.286
| style="text-align:center;" | up unison
| up unison
| style="text-align:center;" | ^1
| ^1
| style="text-align:center;" | D^
| ^D
| augmented 1sn
|-
|-
| style="text-align:center;" | 2
| 2
| style="text-align:center;" | 68.571
| 68.571
| style="text-align:center;" | double-up unison
| dup unison
| style="text-align:center;" | ^^1
| ^^1
| style="text-align:center;" | D^^
| ^^D
| diminished 2nd
|-
|-
| style="text-align:center;" | 3
| 3
| style="text-align:center;" | 102.857
| 102.857
| style="text-align:center;" | double-down 2nd
| dud 2nd
| style="text-align:center;" | vv2
| vv2
| style="text-align:center;" | Evv
| vvE
| minor 2nd
|-
|-
| style="text-align:center;" | 4
| 4
| style="text-align:center;" | 137.143
| 137.143
| style="text-align:center;" | down 2nd
| down 2nd
| style="text-align:center;" | v2
| v2
| style="text-align:center;" | Ev
| vE
| neutral 2nd
|-
|-
| style="text-align:center;" | 5
| 5
| style="text-align:center;" |171.429
| 171.429
| style="text-align:center;" | 2nd
| 2nd
| style="text-align:center;" | 2
| 2
| style="text-align:center;" | E
| E
| submajor 2nd
|-
|-
| style="text-align:center;" | 6
| 6
| style="text-align:center;" | 205.714
| 205.714
| style="text-align:center;" | up 2nd
| up 2nd
| style="text-align:center;" | ^2
| ^2
| style="text-align:center;" | E^
| ^E
| major 2nd
|-
|-
| style="text-align:center;" | 7
| 7
| style="text-align:center;" | 240
| 240
| style="text-align:center;" | double-up 2nd
| dup 2nd
| style="text-align:center;" | ^^2
| ^^2
| style="text-align:center;" | E^^
| ^^E
| supermajor 2nd
|-
|-
| style="text-align:center;" | 8
| 8
| style="text-align:center;" | 274.286
| 274.286
| style="text-align:center;" | double-down 3rd
| dud 3rd
| style="text-align:center;" | vv3
| vv3
| style="text-align:center;" | Fvv
| vvF
| diminished 3rd
|-
|-
| style="text-align:center;" | 9
| 9
| style="text-align:center;" | 308.571
| 308.571
| style="text-align:center;" | down 3rd
| down 3rd
| style="text-align:center;" | v3
| v3
| style="text-align:center;" | Fv
| vF
| minor 3rd
|-
|-
| style="text-align:center;" | 10
| 10
| style="text-align:center;" |342.857
| 342.857
| style="text-align:center;" | 3rd
| 3rd
| style="text-align:center;" | 3
| 3
| style="text-align:center;" | F
| F
| neutral 3rd
|-
|-
| style="text-align:center;" | 11
| 11
| style="text-align:center;" | 377.143
| 377.143
| style="text-align:center;" | up 3rd
| up 3rd
| style="text-align:center;" | ^3
| ^3
| style="text-align:center;" | F^
| ^F
| major 3rd
|-
|-
| style="text-align:center;" | 12
| 12
| style="text-align:center;" | 411.429
| 411.429
| style="text-align:center;" | double-up 3rd
| dup 3rd
| style="text-align:center;" | ^^3
| ^^3
| style="text-align:center;" | F^^
| ^^F
| augmented 3rd
|-
|-
| style="text-align:center;" | 13
| 13
| style="text-align:center;" | 445.714
| 445.714
| style="text-align:center;" | double-down 4th
| dud 4th
| style="text-align:center;" | vv4
| vv4
| style="text-align:center;" | Gvv
| vvG
| diminished 4th
|-
|-
| style="text-align:center;" | 14
| 14
| style="text-align:center;" | 480
| 480
| style="text-align:center;" | down 4th
| down 4th
| style="text-align:center;" | v4
| v4
| style="text-align:center;" | Gv
| vG
| minor 4th
|-
|-
| style="text-align:center;" | 15
| 15
| style="text-align:center;" |514.286
| 514.286
| style="text-align:center;" | 4th
| 4th
| style="text-align:center;" | 4
| 4
| style="text-align:center;" | G
| G
| major 4th
|-
|-
| style="text-align:center;" | 16
| 16
| style="text-align:center;" | 548.571
| 548.571
| style="text-align:center;" | up 4th
| up 4th
| style="text-align:center;" | ^4
| ^4
| style="text-align:center;" | G^
| ^G
| augmented 4th
|-
|-
| style="text-align:center;" | 17
| 17
| style="text-align:center;" | 582.857
| 582.857
| style="text-align:center;" | double-up 4th
| dup 4th
| style="text-align:center;" | ^^4
| ^^4
| style="text-align:center;" | G^^
| ^^G
| minor tritone
|-
|-
| style="text-align:center;" | 18
| 18
| style="text-align:center;" | 617.143
| 617.143
| style="text-align:center;" | double-down 5th
| dud 5th
| style="text-align:center;" | vv5
| vv5
| style="text-align:center;" | Avv
| vvA
| major tritone
|-
|-
| style="text-align:center;" | 19
| 19
| style="text-align:center;" | 651.429
| 651.429
| style="text-align:center;" | down 5th
| down 5th
| style="text-align:center;" | v5
| v5
| style="text-align:center;" | Av
| vA
| diminished 5th
|-
|-
| style="text-align:center;" | 20
| 20
| style="text-align:center;" |685.714
| 685.714
| style="text-align:center;" | 5th
| 5th
| style="text-align:center;" | 5
| 5
| style="text-align:center;" | A
| A
| minor 5th
|-
|-
| style="text-align:center;" | 21
| 21
| style="text-align:center;" | 720
| 720
| style="text-align:center;" | up 5th
| up 5th
| style="text-align:center;" | ^5
| ^5
| style="text-align:center;" | A^
| ^A
| major 5th
|-
|-
| style="text-align:center;" | 22
| 22
| style="text-align:center;" | 754.286
| 754.286
| style="text-align:center;" | double-up 5th
| dup 5th
| style="text-align:center;" | ^^5
| ^^5
| style="text-align:center;" | A^^
| ^^A
| augmented 5th
|-
|-
| style="text-align:center;" | 23
| 23
| style="text-align:center;" | 788.571
| 788.571
| style="text-align:center;" | double-down 6th
| dud 6th
| style="text-align:center;" | vv6
| vv6
| style="text-align:center;" | Bvv
| vvB
| diminished 6th
|-
|-
| style="text-align:center;" | 24
| 24
| style="text-align:center;" | 822.857
| 822.857
| style="text-align:center;" | down 6th
| down 6th
| style="text-align:center;" | v6
| v6
| style="text-align:center;" | Bv
| vB
| minor 6th
|-
|-
| style="text-align:center;" | 25
| 25
| style="text-align:center;" |857.143
| 857.143
| style="text-align:center;" | 6th
| 6th
| style="text-align:center;" | 6
| 6
| style="text-align:center;" | B
| B
| neutral 6th
|-
|-
| style="text-align:center;" | 26
| 26
| style="text-align:center;" | 891.429
| 891.429
| style="text-align:center;" | up 6th
| up 6th
| style="text-align:center;" | ^6
| ^6
| style="text-align:center;" | B^
| ^B
| major 6th
|-
|-
| style="text-align:center;" | 27
| 27
| style="text-align:center;" | 925.714
| 925.714
| style="text-align:center;" | double-up 6th
| dup 6th
| style="text-align:center;" | ^^6
| ^^6
| style="text-align:center;" | B^^
| ^^B
| augmented 6th
|-
|-
| style="text-align:center;" | 28
| 28
| style="text-align:center;" | 960
| 960
| style="text-align:center;" | double-down 7th
| dud 7th
| style="text-align:center;" | vv7
| vv7
| style="text-align:center;" | Cvv
| vvC
| diminished 7th
|-
|-
| style="text-align:center;" | 29
| 29
| style="text-align:center;" | 994.286
| 994.286
| style="text-align:center;" | down 7th
| down 7th
| style="text-align:center;" | v7
| v7
| style="text-align:center;" | Cv
| vC
| minor 7th
|-
|-
| style="text-align:center;" | 30
| 30
| style="text-align:center;" |1028.571
| 1028.571
| style="text-align:center;" | 7th
| 7th
| style="text-align:center;" | 7
| 7
| style="text-align:center;" | C
| C
| superminor 7th
|-
|-
| style="text-align:center;" | 31
| 31
| style="text-align:center;" | 1062.857
| 1062.857
| style="text-align:center;" | up 7th
| up 7th
| style="text-align:center;" | ^7
| ^7
| style="text-align:center;" | C^
| ^C
| neutral 7th
|-
|-
| style="text-align:center;" | 32
| 32
| style="text-align:center;" | 1097.143
| 1097.143
| style="text-align:center;" | double-up 7th
| dup 7th
| style="text-align:center;" | ^^7
| ^^7
| style="text-align:center;" | C^^
| ^^C
| major 7th
|-
|-
| style="text-align:center;" | 33
| 33
| style="text-align:center;" | 1131.429
| 1131.429
| style="text-align:center;" | double-down 8ve
| dud 8ve
| style="text-align:center;" | vv8
| vv8
| style="text-align:center;" | Dvv
| vvD
| augmented 7th
|-
|-
| style="text-align:center;" | 34
| 34
| style="text-align:center;" | 1165.714
| 1165.714
| style="text-align:center;" | down 8ve
| down 8ve
| style="text-align:center;" | v8
| v8
| style="text-align:center;" | Dv
| vD
| diminished 8ve
|-
|-
| style="text-align:center;" | 35
| 35
| style="text-align:center;" | 1200
| 1200
| style="text-align:center;" | 8ve
| 8ve
| style="text-align:center;" | 8
| 8
| style="text-align:center;" | D
| D
| 8ve
|}
|}


==Ups and downs for chords==
===Sagittal notation===
Ups and downs can be used to name 35edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used.
====Best fifth notation====
This notation uses the same sagittal sequence as EDOs [[30edo#Second-best fifth notation|30b]] and [[40edo#Sagittal notation|40]], and is a superset of the notation for [[7edo#Sagittal notation|7-EDO]].
 
<imagemap>
File:35-EDO_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 415 0 575 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 415 106 [[Fractional_3-limit_notation#Bad-fifths_limma-fraction_notation | limma-fraction notation]]
default [[File:35-EDO_Sagittal.svg]]
</imagemap>
 
====Second-best fifth notation====
This notation uses the same sagittal sequence as [[42edo#Sagittal notation|42-EDO]], and is a superset of the notation for [[5edo#Sagittal notation|5-EDO]].
 
<imagemap>
File:35b_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 391 0 551 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 391 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]]
default [[File:35b_Sagittal.svg]]
</imagemap>
 
=== Chord Names ===
Ups and downs can be used to name 35edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are.


0-10-20 = C E G = C = C or C perfect
0-10-20 = C E G = C = C or C perfect


0-9-20 = C Ev G = C(v3) = C down-three
0-9-20 = C vE G = Cv = C down


0-11-20 = C E^ G = C(^3) = C up-three
0-11-20 = C ^E G = C^ = C up


0-10-19 = C E Gv = C(v5) = C down-five
0-10-19 = C E vG = C(v5) = C down-five


0-11-21 = C E^ G^ = C(^3,^5) = C up-three up-five
0-11-21 = C ^E ^G = C^(^5) = C up up-five


0-10-20-30 = C E G B = C7 = C seven
0-10-20-30 = C E G B = C7 = C seven


0-10-20-29 = C E G Bv = C(v7) = C down-seven
0-10-20-29 = C E G vB = C,v7 = C add down-seven


0-9-20-30 = C Ev G B = C7(v3) = C seven down-three
0-9-20-30 = C vE G B = Cv,7 = C down add-seven


0-9-20-29 = C Ev G Bv = C.v7 = C dot down seven
0-9-20-29 = C vE G vB = Cv7 = C down seven


For a more complete list, see [[Ups_and_Downs_Notation#Chord names in other EDOs|Ups and Downs Notation - Chord names in other EDOs]].
For a more complete list, see [[Ups and downs notation#Chords and Chord Progressions|Ups and downs notation - Chords and Chord Progressions]].


=Intervals=
== JI Intervals ==
(Bolded ratio indicates that the ratio is most accurately tuned by the given 35-edo interval.)
(Bolded ratio indicates that the ratio is most accurately tuned by the given 35edo interval.)


{| class="wikitable"
{| class="wikitable"
|-
|-
! | Degrees
| Degrees
! | Cents value
| Cents value
! | Ratios in 2.5.7.11.17 subgroup
| Ratios in 2.5.7.11.17 subgroup
! | Ratios with flat 3
| Ratios with flat 3
! | Ratios with sharp 3
| Ratios with sharp 3
! | Ratios with best 9
| Ratios with best 9
|-
|-
| | 0
| 0
| 0.000
| 0.000
| | '''1/1'''
| '''1/1'''
| | (see comma table)
| (see comma table)
| |  
|  
| |  
|  
|-
|-
| | 1
| 1
| | 34.286
| 34.286
| | '''50/49''', '''121/119''', 33/32
| '''50/49''', '''121/119''', 33/32
| | '''36/35'''
| '''36/35'''
| | 25/24
| 25/24
| | '''81/80'''
| '''81/80'''
|-
|-
| | 2
| 2
| | 68.571
| 68.571
| | 128/125
| 128/125
| | '''25/24'''
| '''25/24'''
| | 81/80
| 81/80
| |  
|  
|-
|-
| | 3
| 3
| | 102.857
| 102.857
| | '''17/16'''
| '''17/16'''
| | '''15/14'''
| '''15/14'''
| | '''16/15'''
| '''16/15'''
| | '''18/17'''
| '''18/17'''
|-
|-
| | 4
| 4
| | 137.143
| 137.143
| |  
|  
| | '''12/11''', 16/15
| '''12/11''', 16/15
| |  
|  
| |  
|  
|-
|-
| | 5
| 5
| |171.429
|171.429
| | '''11/10'''
| '''11/10'''
| |  
|  
| | 12/11
| 12/11
| | '''10/9'''
| '''10/9'''
|-
|-
| | 6
| 6
| | 205.714
| 205.714
| |  
|  
| |  
|  
| |  
|  
| | '''9/8'''
| '''9/8'''
|-
|-
| | 7
| 7
| | 240
| 240
| | '''8/7'''
| '''8/7'''
| |  
|  
| | 7/6
| 7/6
| |  
|  
|-
|-
| | 8
| 8
| | 274.286
| 274.286
| | '''20/17'''
| '''20/17'''
| | '''7/6'''
| '''7/6'''
| |  
|  
| |  
|  
|-
|-
| | 9
| 9
| | 308.571
| 308.571
| |  
|  
| | '''6/5'''
| '''6/5'''
| |  
|  
| |  
|  
|-
|-
| | 10
| 10
| |342.857
|342.857
| | '''17/14'''
| '''17/14'''
| |  
|  
| | 6/5
| 6/5
| | '''11/9'''
| '''11/9'''
|-
|-
| | 11
| 11
| | 377.143
| 377.143
| | '''5/4'''
| '''5/4'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 12
| 12
| | 411.429
| 411.429
| | '''14/11'''
| '''14/11'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 13
| 13
| | 445.714
| 445.714
| | '''22/17''', 32/25
| '''22/17''', 32/25
| |  
|  
| |  
|  
| | '''9/7'''
| '''9/7'''
|-
|-
| | 14
| 14
| | 480
| 480
| |  
|  
| |  
|  
| | 4/3, '''21/16'''
| 4/3, '''21/16'''
| |  
|  
|-
|-
| | 15
| 15
| |514.286
|514.286
| |  
|  
| | '''4/3'''
| '''4/3'''
| |  
|  
| |  
|  
|-
|-
| | 16
| 16
| | 548.571
| 548.571
| | '''11/8'''
| '''11/8'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 17
| 17
| | 582.857
| 582.857
| | '''7/5'''
| '''7/5'''
| | '''24/17'''
| '''24/17'''
| | 17/12
| 17/12
| |  
|  
|-
|-
| | 18
| 18
| | 617.143
| 617.143
| | '''10/7'''
| '''10/7'''
| | '''17/12'''
| '''17/12'''
| | 24/17
| 24/17
| |  
|  
|-
|-
| | 19
| 19
| | 651.429
| 651.429
| | '''16/11'''
| '''16/11'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 20
| 20
| |685.714
|685.714
| |  
|  
| | '''3/2'''
| '''3/2'''
| |  
|  
| |  
|  
|-
|-
| | 21
| 21
| | 720
| 720
| |  
|  
| |  
|  
| | 3/2, '''32/21'''
| 3/2, '''32/21'''
| |  
|  
|-
|-
| | 22
| 22
| | 754.286
| 754.286
| | '''17/11''', 25/16
| '''17/11''', 25/16
| |  
|  
| |  
|  
| | '''14/9'''
| '''14/9'''
|-
|-
| | 23
| 23
| | 788.571
| 788.571
| | '''11/7'''
| '''11/7'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 24
| 24
| | 822.857
| 822.857
| | '''8/5'''
| '''8/5'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 25
| 25
| |857.143
|857.143
| | '''28/17'''
| '''28/17'''
| |  
|  
| | 5/3
| 5/3
| | '''18/11'''
| '''18/11'''
|-
|-
| | 26
| 26
| | 891.429
| 891.429
| |  
|  
| | '''5/3'''
| '''5/3'''
| |  
|  
| |  
|  
|-
|-
| | 27
| 27
| | 925.714
| 925.714
| | '''17/10'''
| '''17/10'''
| | '''12/7'''
| '''12/7'''
| |  
|  
| |  
|  
|-
|-
| | 28
| 28
| | 960
| 960
| | '''7/4'''
| '''7/4'''
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 29
| 29
| | 994.286
| 994.286
| |  
|  
| |  
|  
| |  
|  
| | '''16/9'''
| '''16/9'''
|-
|-
| | 30
| 30
| |1028.571
|1028.571
| | '''20/11'''
| '''20/11'''
| |  
|  
| |  
|  
| | '''9/5'''
| '''9/5'''
|-
|-
| | 31
| 31
| | 1062.857
| 1062.857
| |  
|  
| | '''11/6''', 15/8
| '''11/6''', 15/8
| |  
|  
| |  
|  
|-
|-
| | 32
| 32
| | 1097.143
| 1097.143
| | '''32/17'''
| '''32/17'''
| | '''28/15'''
| '''28/15'''
| | '''15/8'''
| '''15/8'''
| | '''17/9'''
| '''17/9'''
|-
|-
| | 33
| 33
| | 1131.429
| 1131.429
| |  
|  
| |  
|  
| |  
|  
| |  
|  
|-
|-
| | 34
| 34
| | 1165.714
| 1165.714
| |  
|  
| |  
|  
| |  
|  
| |  
|  
|-
|-
|3
|3
Line 516: Line 588:
|}
|}


=Rank two temperaments=
{{15-odd-limit|35}}


== Regular temperament properties ==
=== Rank-2 temperaments ===
{| class="wikitable"
{| class="wikitable"
|-
|-
! | Periods
! Periods<br>per 8ve
 
! Generator
per octave
! Temperaments with<br>flat 3/2 (patent val)
! | Generator
! Temperaments with sharp 3/2 (35b val)
! | Temperaments with
! [[Mos scale]]s
 
flat 3/2 (patent val)
! | <span style="display: block; text-align: center;">Temperaments with sharp 3/2 (35b val)</span>
|-
|-
| | 1
| 1
| | 1\35
| 1\35
| |  
|  
| |  
|  
|  
|-
|-
| | 1
| 1
| | 2\35
| 2\35
| |  
|  
| |
|  
| [[1L 16s]], [[17L 1s]]
|-
|-
| | 1
| 1
| | 3\35
| 3\35
| |  
|  
| | [[Ripple|Ripple]]
| [[Ripple]]
| [[1L 10s]], [[11L 1s]], [[12L 11s]]
|-
|-
| | 1
| 1
| | 4\35
| 4\35
| | [[Greenwoodmic_temperaments#Secund|Secund]]
| [[Secund]]
| |  
|  
| [[1L 7s]], [[8L 1s]], [[9L 8s]], [[9L 17s]]
|-
|-
| | 1
| 1
| | 6\35
| 6\35
| colspan="2" | Messed-up [[Chromatic_pairs#Baldy|Baldy]]
| colspan="2" | [[Baldy]] (messed-up)
| [[1L 4s]], [[5L 1s]], [[6L 5s]], [[6L 11s]], [[6L 17s]], [[6L 23s]]
|-
|-
| | 1
| 1
| | 8\35
| 8\35
| |  
|  
| | Messed-up [[Orwell]]
| [[Orwell]] (messed-up)
| [[1L 3s]], [[4L 1s]], [[4L 5s]], [[9L 4s]], [[13L 9s]]
|-
|-
| | 1
| 1
| | 9\35
| 9\35
| | [[Myna|Myna]]
| [[Myna]]
| |  
|  
| [[1L 3s]], [[4L 3s]], [[4L 7s]], [[4L 11s]], [[4L 15s]], …, [[4L 27s]]
|-
|-
| | 1
| 1
| | 11\35
| 11\35
| | [[Muggles]]
| [[Muggles]]
| |  
|  
| [[3L 1s]], [[3L 4s]], [[3L 7s]] [[3L 10s]], [[3L 13s]], [[16L 3s]]
|-
|-
| | 1
| 1
| | 12\35
| 12\35
| |  
|  
| | [[Avicennmic_temperaments#Roman|Roman]]
| [[Roman]]
| [[2L 1s]], [[3L 2s]], [[3L 5s]], [[3L 8s]], [[3L 11s]], [[3L 14s]], [[3L 17s]], [[3L 20s]], …, [[3L 29s]]
|-
|-
| | 1
| 1
| | 13\35
| 13\35
| colspan="2" | Inconsistent 2.9'/7.5/3 [[Sensi]]
| colspan="2" | Inconsistent 2.9'/7.5/3 [[sensi]]
| [[2L 1s]], [[3L 2s]], [[3L 5s]], [[8L 3s]], [[8L 11s]], [[8L 19s]]
|-
|-
| | 1
| 1
| | 16\35
| 16\35
| |  
|  
| |
|  
| [[2L 1s]], [[2L 3s]], [[2L 5s]], [[2L 7s]], [[2L 9s]], [[11L 2s]], [[11L 13s]]
|-
|-
| | 1
| 1
| | 17\35
| 17\35
| |  
|  
| |
|  
| [[2L 1s]], [[2L 3s]], [[2L 5s]], [[2L 7s]], [[2L 9s]], [[2L 11s]], [[2L 13s]], [[2L 15s]], [[2L 17s]], [[2L 19s]], …, [[2L 31s]]
|-
|-
| | 5
| 5
| | 1\35
| 1\35
| |  
|  
| | [[Blackwood]] (favoring 7/6)
| [[Blackwood]] (favoring 7/6)
| [[5L 5s]], [[5L 10s]], [[5L 15s]], [[5L 20s]], [[5L 25s]]
|-
|-
| | 5
| 5
| | 2\35
| 2\35
| |  
|  
| | [[Blackwood]] (favoring 6/5 and 20/17)
| [[Blackwood]] (favoring 6/5 and 20/17)
| [[5L 5s]], [[5L 10s]], [[15L 5s]]
|-
|-
| | 5
| 5
| | 3\35
| 3\35
| |  
|  
| | [[Blackwood]] (favoring 5/4 and 17/14)
| [[Blackwood]] (favoring 5/4 and 17/14)
| [[5L 5s]], [[10L 5s]], [[10L 15s]]
|-
|-
| | 7
| 7
| | 1\35
| 1\35
| | [[Apotome_family|Whitewood]]/[[Apotome_family#Redwood|Redwood]]
| [[Whitewood]] / [[redwood]]
| |  
|  
| [[7L 7s]], [[7L 14s]], [[7L 21s]]
|-
|-
| | 7
| 7
| | 2\35
| 2\35
| | [[Greenwoodmic_temperaments#Greenwood|Greenwood]]
| [[Greenwood]]
| |  
|  
| [[7L 7s]], [[14L 7s]]
|}
|}


=Scales=
=== Commas ===
A good beginning for start to play 35-EDO is with the Sub-diatonic scale, that is a [[MOS]] of 3L2s: 9 4 9 9 4.
35et [[tempering out|tempers out]] the following [[comma]]s. (Note: This assumes the [[val]] {{val| 35 55 81 98 121 130 }}.)
 
=Commas=
35EDO tempers out the following commas. (Note: This assumes the val &lt; 35 55 81 98 121 130|.)


{| class="wikitable"
{| class="commatable wikitable center-1 center-2 right-4 center-5"
|-
|-
! | Comma
! [[Harmonic limit|Prime<br>limit]]
! | Monzo
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! | Value (Cents)
! [[Monzo]]
! | Name 1
! [[Cent]]s
! | Name 2
! [[Color name]]
! Name(s)
|-
|-
| style="text-align:center;" | 2187/2048
| 3
| |<nowiki> | -11 7 </nowiki>&gt;
| [[2187/2048]]
| style="text-align:right;" | 113.69
| {{monzo| -11 7 }}
| style="text-align:center;" | Apotome
| 113.69
| style="text-align:center;" | Whitewood comma
| Lawa
| Whitewood comma, apotome, Pythagorean chroma
|-
|-
| style="text-align:center;" | 6561/6250
| 5
| |<nowiki> | -1 8 -5 </nowiki>&gt;
| [[6561/6250]]
| style="text-align:right;" | 84.07
| {{monzo| -1 8 -5 }}
| style="text-align:center;" | Ripple comma
| 84.07
| style="text-align:center;" |
| Quingu
| Ripple comma
|-
|-
| style="text-align:center;" | 10077696/9765625
| 5
| |<nowiki> | 9 9 -10 </nowiki>&gt;
| <abbr title="10077696/9765625">(15 digits)</abbr>
| style="text-align:right;" | 54.46
| {{monzo| 9 9 -10 }}
| style="text-align:center;" | Mynic comma
| 54.46
| style="text-align:center;" |
| Quinbigu
| [[Mynic comma]]
|-
|-
| style="text-align:center;" | 3125/3072
| 5
| |<nowiki> | -10 -1 5 </nowiki>&gt;
| [[3125/3072]]
| style="text-align:right;" | 29.61
| {{monzo| -10 -1 5 }}
| style="text-align:center;" | Small diesis
| 29.61
| style="text-align:center;" | Magic comma
| Laquinyo
| Magic comma, small diesis
|-
|-
| style="text-align:center;" | 405/392
| 7
| |<nowiki> | -3 4 1 -2 </nowiki>&gt;
| [[405/392]]
| style="text-align:right;" | 56.48
| {{monzo| -3 4 1 -2 }}
| style="text-align:center;" | Greenwoodma
| 56.48
| style="text-align:center;" |
| Ruruyo
| Greenwoodma
|-
|-
| style="text-align:center;" | 16807/16384
| 7
| |<nowiki> | -14 0 0 5 </nowiki>&gt;
| [[16807/16384]]
| style="text-align:right;" | 44.13
| {{monzo| -14 0 0 5 }}
| style="text-align:center;" |
| 44.13
| style="text-align:center;" |
| Laquinzo
| Cloudy comma
|-
|-
| style="text-align:center;" | 525/512
| 7
| |<nowiki> | -9 1 2 1 </nowiki>&gt;
| [[525/512]]
| style="text-align:right;" | 43.41
| {{monzo| -9 1 2 1 }}
| style="text-align:center;" | Avicenna
| 43.41
| style="text-align:center;" |
| Lazoyoyo
| Avicennma
|-
|-
| style="text-align:center;" | 126/125
| 7
| |<nowiki> | 1 2 -3 1 </nowiki>&gt;
| [[126/125]]
| style="text-align:right;" | 13.79
| {{monzo| 1 2 -3 1 }}
| style="text-align:center;" | Starling comma
| 13.79
| style="text-align:center;" | Septimal semicomma
| Zotrigu
| Septimal semicomma, starling comma
|-
|-
| style="text-align:center;" | 99/98
| 11
| |<nowiki> | -1 2 0 -2 1 </nowiki>&gt;
| [[99/98]]
| style="text-align:right;" | 17.58
| {{monzo| -1 2 0 -2 1 }}
| style="text-align:center;" | Mothwellsma
| 17.58
| style="text-align:center;" |
| Loruru
| Mothwellsma
|-
|-
| style="text-align:center;" | 66/65
| 13
| |<nowiki> | 1 1 -1 0 1 -1 </nowiki>&gt;
| [[66/65]]
| style="text-align:right;" | 26.43
| {{monzo| 1 1 -1 0 1 -1 }}
| style="text-align:center;" |
| 26.43
| style="text-align:center;" |
| Thulogu
| Winmeanma
|}
|}
<references/>
== Scales ==
* A good place to start using 35-EDO is with the sub-diatonic scale, that is a [[MOS]] of 3L2s: 9 4 9 9 4.
* Also available is the amulet scale{{idiosyncratic}}, approximated from [[magic]] in [[25edo]]: 3 1 3 3 1 3 4 3 3 1 3 4 3
* Approximations of [[gamelan]] scales:
** 5-tone pelog: 3 5 12 3 12
** 7-tone pelog: 3 5 7 5 3 8 4
** 5-tone slendro: 7 7 7 7 7
== Instruments ==
=== Lumatone ===
35edo can be played on the [[Lumatone]]. See [[Lumatone mapping for 35edo]]
=== Skip fretting ===
'''Skip fretting system 35 3 8''' is a [[skip fretting]] system for [[35edo]]. All examples on this page are for 7-string [[guitar]].
; Prime harmonics
1/1: string 2 open
2/1: string 3 fret 9 and string 6 fret 1
3/2: string 3 fret 4 and string 4 fret 13
5/4: string 3 fret 1, string 4 fret 10, and string 7 fret 2
7/4: string 4 fret 4
11/8: string 1 fret 8, string 4 open, and string 5 fret 9
13/8: string 1 fret 11, string 4 fret 3, and string 5 fret 12
17/16: string 2 fret 1 and string 3 fret 10
== Music ==
; [[dotuXil]]
* [https://www.youtube.com/watch?v=61ssLv9H6rk "Icebound Gallery of Refractions"] from [https://dotuxil.bandcamp.com/album/collected-refractions ''Collected Refractions''] (2024)
; [[E8 Heterotic]]
* [https://youtu.be/07-wj6BaTOw ''G2 Manifold''] (2020) – uses a combination of 5edo and 7edo, which can be classified as a 35edo subset.
; [[JUMBLE]]
* [https://www.youtube.com/watch?v=2qpsI26JfjY ''Penguins...?''] (2024)
; [[Chuckles McGee]]
* [https://www.archive.org/download/Transcendissonance/05Self-destructingMechanicalForest-CityOfTheAsleep.mp3 Self-Destructing Mechanical Forest] (in Secund[9])


=Music=
; [[Claudi Meneghin]]
[http://soonlabel.com/xenharmonic/archives/2348 Little Prelude &amp; Fugue, "The Bijingle" by Claudi Meneghin]
* [https://web.archive.org/web/20190412163316/http://soonlabel.com/xenharmonic/archives/2348'' Little Prelude &amp; Fugue, "The Bijingle"''] (2014)
* [https://www.youtube.com/watch?v=JPie2YDwA8I ''MicroFugue on Happy Birthday for Baroque Ensemble''] (2023)


[http://www.archive.org/download/Transcendissonance/05Self-destructingMechanicalForest-CityOfTheAsleep.mp3 Self-Destructing Mechanical Forest] by Chuckles McGee (in Secund[9])
; [[No Clue Music]]
* [https://www.youtube.com/watch?v=zMUQWdFRGao ''DarkSciFiThing''] (2024)


[[Category:35edo]]
[[Category:Listen]]
[[Category:edo]]
[[Category:listen]]
[[Category:theory]]

Latest revision as of 01:07, 20 August 2025

← 34edo 35edo 36edo →
Prime factorization 5 × 7
Step size 34.2857 ¢ 
Fifth 20\35 (685.714 ¢) (→ 4\7)
Semitones (A1:m2) 0:5 (0 ¢ : 171.4 ¢)
Dual sharp fifth 21\35 (720 ¢) (→ 3\5)
Dual flat fifth 20\35 (685.714 ¢) (→ 4\7)
Dual major 2nd 6\35 (205.714 ¢)
(semiconvergent)
Consistency limit 7
Distinct consistency limit 7

35 equal divisions of the octave (abbreviated 35edo or 35ed2), also called 35-tone equal temperament (35tet) or 35 equal temperament (35et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 35 equal parts of about 34.3 ¢ each. Each step represents a frequency ratio of 21/35, or the 35th root of 2.

Theory

As 35 is 5 times 7, 35edo allows for mixing the two smallest xenharmonic macrotonal edos: 5edo and 7edo. A single degree of 35edo represents the difference between 7edo's narrow fifth of 685.71 ¢ and 5edo's wide fifth of 720 ¢. Because it includes 7edo, 35edo tunes the 29th harmonic with only 1 ¢ of error.

35edo can also represent the 2.3.5.7.11.17 subgroup and 2.9.5.7.11.17 subgroup, because of the accuracy of 9 and the flatness of all other subgroup generators (7/5 and 17/11 stand out, having less than 1 cent error). Therefore among whitewood tunings it is very versatile; you can switch between these different subgroups if you don't mind having to use two different 3/2s to reach the inconsistent 9 (a characteristic of whitewood tunings), and if you ignore 22edo's more in-tune versions of 35edo MOS's and consistent representation of both subgroups.

35edo has the optimal patent val for greenwood and secund temperaments, as well as 11-limit muggles, and the 35f val is an excellent tuning for 13-limit muggles. 35edo is the largest edo with a lack of a diatonic scale (unless 7edo is considered a diatonic scale).

Odd harmonics

Approximation of odd harmonics in 35edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -16.2 -9.2 -8.8 +1.8 -2.7 +16.6 +8.9 -2.1 +11.1 +9.2 -11.1
Relative (%) -47.4 -26.7 -25.7 +5.3 -8.0 +48.5 +25.9 -6.1 +32.3 +26.9 -32.5
Steps
(reduced) 		55
(20) 		81
(11) 		98
(28) 		111
(6) 		121
(16) 		130
(25) 		137
(32) 		143
(3) 		149
(9) 		154
(14) 		158
(18)

Notation

The 7edo fifth is preferred as the diatonic generator for ups and downs notation due to being much easier to notate than the 5edo fifth (which involves E and F being enharmonic), as well as being closer to 3/2.

Degrees Cents Ups and downs notation Dual-fifth notation

based on closest 12edo interval

0 0.000 unison 1 D 1sn, prime
1 34.286 up unison ^1 ^D augmented 1sn
2 68.571 dup unison ^^1 ^^D diminished 2nd
3 102.857 dud 2nd vv2 vvE minor 2nd
4 137.143 down 2nd v2 vE neutral 2nd
5 171.429 2nd 2 E submajor 2nd
6 205.714 up 2nd ^2 ^E major 2nd
7 240 dup 2nd ^^2 ^^E supermajor 2nd
8 274.286 dud 3rd vv3 vvF diminished 3rd
9 308.571 down 3rd v3 vF minor 3rd
10 342.857 3rd 3 F neutral 3rd
11 377.143 up 3rd ^3 ^F major 3rd
12 411.429 dup 3rd ^^3 ^^F augmented 3rd
13 445.714 dud 4th vv4 vvG diminished 4th
14 480 down 4th v4 vG minor 4th
15 514.286 4th 4 G major 4th
16 548.571 up 4th ^4 ^G augmented 4th
17 582.857 dup 4th ^^4 ^^G minor tritone
18 617.143 dud 5th vv5 vvA major tritone
19 651.429 down 5th v5 vA diminished 5th
20 685.714 5th 5 A minor 5th
21 720 up 5th ^5 ^A major 5th
22 754.286 dup 5th ^^5 ^^A augmented 5th
23 788.571 dud 6th vv6 vvB diminished 6th
24 822.857 down 6th v6 vB minor 6th
25 857.143 6th 6 B neutral 6th
26 891.429 up 6th ^6 ^B major 6th
27 925.714 dup 6th ^^6 ^^B augmented 6th
28 960 dud 7th vv7 vvC diminished 7th
29 994.286 down 7th v7 vC minor 7th
30 1028.571 7th 7 C superminor 7th
31 1062.857 up 7th ^7 ^C neutral 7th
32 1097.143 dup 7th ^^7 ^^C major 7th
33 1131.429 dud 8ve vv8 vvD augmented 7th
34 1165.714 down 8ve v8 vD diminished 8ve
35 1200 8ve 8 D 8ve

Sagittal notation

Best fifth notation

This notation uses the same sagittal sequence as EDOs 30b and 40, and is a superset of the notation for 7-EDO.

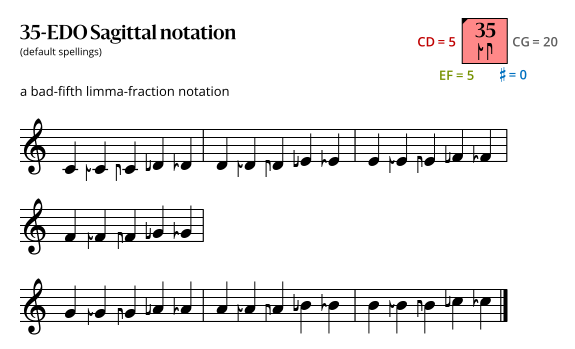
Sagittal notationPeriodic table of EDOs with sagittal notationlimma-fraction notation

Second-best fifth notation

This notation uses the same sagittal sequence as 42-EDO, and is a superset of the notation for 5-EDO.

Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation

Chord Names

Ups and downs can be used to name 35edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are.

0-10-20 = C E G = C = C or C perfect

0-9-20 = C vE G = Cv = C down

0-11-20 = C ^E G = C^ = C up

0-10-19 = C E vG = C(v5) = C down-five

0-11-21 = C ^E ^G = C^(^5) = C up up-five

0-10-20-30 = C E G B = C7 = C seven

0-10-20-29 = C E G vB = C,v7 = C add down-seven

0-9-20-30 = C vE G B = Cv,7 = C down add-seven

0-9-20-29 = C vE G vB = Cv7 = C down seven

For a more complete list, see Ups and downs notation - Chords and Chord Progressions.

JI Intervals

(Bolded ratio indicates that the ratio is most accurately tuned by the given 35edo interval.)

Degrees Cents value Ratios in 2.5.7.11.17 subgroup Ratios with flat 3 Ratios with sharp 3 Ratios with best 9
0 0.000 1/1 (see comma table)
1 34.286 50/49, 121/119, 33/32 36/35 25/24 81/80
2 68.571 128/125 25/24 81/80
3 102.857 17/16 15/14 16/15 18/17
4 137.143 12/11, 16/15
5 171.429 11/10 12/11 10/9
6 205.714 9/8
7 240 8/7 7/6
8 274.286 20/17 7/6
9 308.571 6/5
10 342.857 17/14 6/5 11/9
11 377.143 5/4
12 411.429 14/11
13 445.714 22/17, 32/25 9/7
14 480 4/3, 21/16
15 514.286 4/3
16 548.571 11/8
17 582.857 7/5 24/17 17/12
18 617.143 10/7 17/12 24/17
19 651.429 16/11
20 685.714 3/2
21 720 3/2, 32/21
22 754.286 17/11, 25/16 14/9
23 788.571 11/7
24 822.857 8/5
25 857.143 28/17 5/3 18/11
26 891.429 5/3
27 925.714 17/10 12/7
28 960 7/4
29 994.286 16/9
30 1028.571 20/11 9/5
31 1062.857 11/6, 15/8
32 1097.143 32/17 28/15 15/8 17/9
33 1131.429
34 1165.714
3 1200

The following tables show how 15-odd-limit intervals are represented in 35edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 35edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
7/5, 10/7 0.345 1.0
13/12, 24/13 1.430 4.2
9/8, 16/9 1.804 5.3
11/8, 16/11 2.747 8.0
11/9, 18/11 4.551 13.3
11/7, 14/11 6.079 17.7
11/10, 20/11 6.424 18.7
5/3, 6/5 7.070 20.6
7/6, 12/7 7.415 21.6
15/13, 26/15 7.741 22.6
13/10, 20/13 8.500 24.8
7/4, 8/7 8.826 25.7
13/7, 14/13 8.845 25.8
15/8, 16/15 8.874 25.9
5/4, 8/5 9.171 26.7
9/7, 14/9 10.630 31.0
9/5, 10/9 10.975 32.0
15/11, 22/15 11.621 33.9
11/6, 12/11 13.494 39.4
13/9, 18/13 14.811 43.2
13/11, 22/13 14.924 43.5
3/2, 4/3 16.241 47.4
15/14, 28/15 16.586 48.4
13/8, 16/13 16.615 48.5
15-odd-limit intervals in 35edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
7/5, 10/7 0.345 1.0
11/8, 16/11 2.747 8.0
11/7, 14/11 6.079 17.7
11/10, 20/11 6.424 18.7
5/3, 6/5 7.070 20.6
7/6, 12/7 7.415 21.6
7/4, 8/7 8.826 25.7
5/4, 8/5 9.171 26.7
11/6, 12/11 13.494 39.4
3/2, 4/3 16.241 47.4
15/14, 28/15 16.586 48.4
13/8, 16/13 16.615 48.5
13/11, 22/13 19.362 56.5
15/11, 22/15 22.665 66.1
9/5, 10/9 23.311 68.0
9/7, 14/9 23.656 69.0
15/8, 16/15 25.412 74.1
13/7, 14/13 25.441 74.2
13/10, 20/13 25.786 75.2
11/9, 18/11 29.735 86.7
9/8, 16/9 32.481 94.7
13/12, 24/13 32.856 95.8
15/13, 26/15 42.027 122.6
13/9, 18/13 49.097 143.2

Regular temperament properties

Rank-2 temperaments

Periods
per 8ve 		Generator Temperaments with
flat 3/2 (patent val) 		Temperaments with sharp 3/2 (35b val) Mos scales
1 1\35
1 2\35 1L 16s, 17L 1s
1 3\35 Ripple 1L 10s, 11L 1s, 12L 11s
1 4\35 Secund 1L 7s, 8L 1s, 9L 8s, 9L 17s
1 6\35 Baldy (messed-up) 1L 4s, 5L 1s, 6L 5s, 6L 11s, 6L 17s, 6L 23s
1 8\35 Orwell (messed-up) 1L 3s, 4L 1s, 4L 5s, 9L 4s, 13L 9s
1 9\35 Myna 1L 3s, 4L 3s, 4L 7s, 4L 11s, 4L 15s, …, 4L 27s
1 11\35 Muggles 3L 1s, 3L 4s, 3L 7s 3L 10s, 3L 13s, 16L 3s
1 12\35 Roman 2L 1s, 3L 2s, 3L 5s, 3L 8s, 3L 11s, 3L 14s, 3L 17s, 3L 20s, …, 3L 29s
1 13\35 Inconsistent 2.9'/7.5/3 sensi 2L 1s, 3L 2s, 3L 5s, 8L 3s, 8L 11s, 8L 19s
1 16\35 2L 1s, 2L 3s, 2L 5s, 2L 7s, 2L 9s, 11L 2s, 11L 13s
1 17\35 2L 1s, 2L 3s, 2L 5s, 2L 7s, 2L 9s, 2L 11s, 2L 13s, 2L 15s, 2L 17s, 2L 19s, …, 2L 31s
5 1\35 Blackwood (favoring 7/6) 5L 5s, 5L 10s, 5L 15s, 5L 20s, 5L 25s
5 2\35 Blackwood (favoring 6/5 and 20/17) 5L 5s, 5L 10s, 15L 5s
5 3\35 Blackwood (favoring 5/4 and 17/14) 5L 5s, 10L 5s, 10L 15s
7 1\35 Whitewood / redwood 7L 7s, 7L 14s, 7L 21s
7 2\35 Greenwood 7L 7s, 14L 7s

Commas

35et tempers out the following commas. (Note: This assumes the val ⟨35 55 81 98 121 130].)

Prime
limit 		Ratio[1] Monzo Cents Color name Name(s)
3 2187/2048 [-11 7⟩ 113.69 Lawa Whitewood comma, apotome, Pythagorean chroma
5 6561/6250 [-1 8 -5⟩ 84.07 Quingu Ripple comma
5 (15 digits) [9 9 -10⟩ 54.46 Quinbigu Mynic comma
5 3125/3072 [-10 -1 5⟩ 29.61 Laquinyo Magic comma, small diesis
7 405/392 [-3 4 1 -2⟩ 56.48 Ruruyo Greenwoodma
7 16807/16384 [-14 0 0 5⟩ 44.13 Laquinzo Cloudy comma
7 525/512 [-9 1 2 1⟩ 43.41 Lazoyoyo Avicennma
7 126/125 [1 2 -3 1⟩ 13.79 Zotrigu Septimal semicomma, starling comma
11 99/98 [-1 2 0 -2 1⟩ 17.58 Loruru Mothwellsma
13 66/65 [1 1 -1 0 1 -1⟩ 26.43 Thulogu Winmeanma
  1. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Scales

  • A good place to start using 35-EDO is with the sub-diatonic scale, that is a MOS of 3L2s: 9 4 9 9 4.
  • Also available is the amulet scale[idiosyncratic term], approximated from magic in 25edo: 3 1 3 3 1 3 4 3 3 1 3 4 3
  • Approximations of gamelan scales:
    • 5-tone pelog: 3 5 12 3 12
    • 7-tone pelog: 3 5 7 5 3 8 4
    • 5-tone slendro: 7 7 7 7 7

Instruments

Lumatone

35edo can be played on the Lumatone. See Lumatone mapping for 35edo

Skip fretting

Skip fretting system 35 3 8 is a skip fretting system for 35edo. All examples on this page are for 7-string guitar.

Prime harmonics

1/1: string 2 open

2/1: string 3 fret 9 and string 6 fret 1

3/2: string 3 fret 4 and string 4 fret 13

5/4: string 3 fret 1, string 4 fret 10, and string 7 fret 2

7/4: string 4 fret 4

11/8: string 1 fret 8, string 4 open, and string 5 fret 9

13/8: string 1 fret 11, string 4 fret 3, and string 5 fret 12

17/16: string 2 fret 1 and string 3 fret 10

Music

dotuXil
E8 Heterotic
  • G2 Manifold (2020) – uses a combination of 5edo and 7edo, which can be classified as a 35edo subset.
JUMBLE
Chuckles McGee
Claudi Meneghin
No Clue Music
Retrieved from "https://en.xen.wiki/index.php?title=35edo&oldid=207603"