Hendecatonic MOS: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Wikispaces>Andrew_Heathwaite
**Imported revision 278681256 - Original comment: **
BudjarnLambeth (talk | contribs)
autopatrolled
18,189 edits
m Categorised this uncategorised page
 
(16 intermediate revisions by 3 users not shown)
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
[[File:hendecatonic_MOS_scales_PING.png|alt=hendecatonic_MOS_scales_PING.png|hendecatonic_MOS_scales_PING.png]]
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
 
: This revision was by author [[User:Andrew_Heathwaite|Andrew_Heathwaite]] and made on <tt>2011-11-24 00:03:29 UTC</tt>.<br>
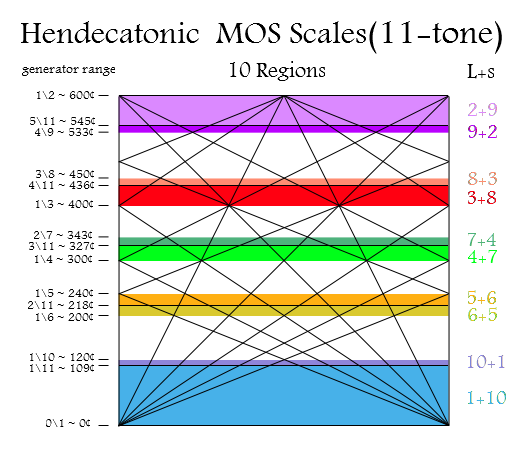
Hendecatonic (11-tone) [[MOSScales|MOS Scales]] come in many varieties and are effective as chromatic scales out of which albitonic (diatonic-like) subsets can be taken. As 11 is a prime number, each Hendecatonic MOS Scale has the octave as a period, rather than some division of the octave like 600¢. It is a simple matter to retune a Halberstadt keyboard to a Hendecatonic MOS Scale, with the 2/1 occurring after 11 keys, or by skipping a key so the 2/1 occurs after 12 keys. The diagram above shows the 10 generator ranges ("Regions") where Hendecatonic MOS Scales occur.
: The original revision id was <tt>278681256</tt>.<br>
 
: The revision comment was: <tt></tt><br>
See: [[Chromatic_pairs|chromatic pairs]], [[Tridecatonic_MOS|tridecatonic MOS]]
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
 
<h4>Original Wikitext content:</h4>
=The 10 Generator Ranges=
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">[[image:hendecatonic_MOS_scales_corrected.jpg]]</pre></div>
 
<h4>Original HTML content:</h4>
==[[1L_10s|1L 10s]] aka 1+10==
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;Hendecatonic MOS&lt;/title&gt;&lt;/head&gt;&lt;body&gt;&lt;!-- ws:start:WikiTextLocalImageRule:0:&amp;lt;img src=&amp;quot;/file/view/hendecatonic_MOS_scales_corrected.jpg/278681228/hendecatonic_MOS_scales_corrected.jpg&amp;quot; alt=&amp;quot;&amp;quot; title=&amp;quot;&amp;quot; /&amp;gt; --&gt;&lt;img src="/file/view/hendecatonic_MOS_scales_corrected.jpg/278681228/hendecatonic_MOS_scales_corrected.jpg" alt="hendecatonic_MOS_scales_corrected.jpg" title="hendecatonic_MOS_scales_corrected.jpg" /&gt;&lt;!-- ws:end:WikiTextLocalImageRule:0 --&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>
 
Range: 0¢ to 109.091¢ (1\[[11edo|11edo]])
 
Albitonic MOS subsets: [[1L_6s|1L 6s]], [[1L_7s|1L 7s]], [[1L_8s|1L 8s]] etc.
 
[[Valentine|Valentine]][11] in [[46edo|46edo]] (g=3\46 ~ 78.261¢): 3 3 3 3 3 3 3 3 3 16 3
 
[[Nautilus|Nautilus]][11] in [[29edo|29edo]] (g=2\29 ~ 82.759¢): 2 2 2 9 2 2 2 2 2 2
 
[[Octacot|Octacot]][11] in [[41edo|41edo]] (g=3\41 ~ 88.805¢): 3 3 3 3 3 3 3 3 3 3 11
 
[[Passion|Passion]][11] in [[37edo|37edo]] (g=3\37 ~ 97.297¢): 3 3 3 3 3 3 3 3 3 3 7
 
[[Ripple|Ripple]][11] in [[23edo|23edo]] (g=2\23 ~ 104.348¢): 2 2 2 2 2 2 2 2 2 2 3
 
==[[10L_1s|10L 1s]] aka 10+1==
 
Range: 109.091¢ (1\11edo) to 120¢ (1\[[10edo|10edo]])
 
Albitonic MOS subsets: [[1L_6s|1L 6s]], [[1L_7s|1L 7s]], [[1L_8s|1L 8s]] etc.
 
[[Miracle|Miracle]][11] in [[72edo|72edo]] (g=7\72 ~ 116.667¢): 7 7 7 7 7 7 7 2 7 7 7
 
==[[6L_5s|6L 5s]] aka 6+5==
 
Range: 200¢ (1\[[6edo|6edo]]) to 218.182¢ (2\11edo)
 
Albitonic MOS subsets: [[5L_1s|5L 1s]]
 
[[baldy11|Baldy]][11] in [[47edo|47edo]] (g=8\47 ~ 204.255¢): 7 1 7 1 7 1 7 7 1 7 1
 
[[machine11|Machine]][11] in [[28edo|28edo]] (g=5\28 ~ 214.286¢): 3 2 3 2 3 2 3 3 2 3 2
 
==[[5L_6s|5L 6s]] aka 5+6==
 
Range: 218.182¢ (2\11edo) to 240¢ (1\[[5edo|5edo]])
 
Albitonic MOS subsets: [[5L_1s|5L 1s]]
 
[[Gorgo|Gorgo]][11]/[[shoe11|Shoe]][11] in [[37edo|37edo]] (g=7\37 ~ 227.027¢): 5 2 5 2 5 2 5 2 2 5 2
 
[[Cynder|Cynder]][11]/[[Mothra|Mothra]][11]/[[Slendric|Slendric]][11] in [[31edo|31edo]] (g=6\31 ~ 232.258¢): 1 5 1 5 1 5 1 5 1 1 5
 
[[Rodan|Rodan]][11] in [[41edo|41edo]] (g=8\41 ~ 234.146¢): 1 7 1 7 1 7 1 7 1 1 7
 
==[[4L_7s|4L 7s]] aka 4+7==
 
Range: 300¢ (1\[[4edo|4edo]]) to 327.273¢ (3\11edo)
 
Albitonic MOS subsets: [[4L_3s|4L 3s]]
 
[[Myna|Myna]][11] in [[89edo|89edo]]: 3 3 17 3 3 17 3 3 17 3 17
 
[[Keemun|Keemun]][11]/[[Hanson|Hanson]][11]/[[catakleismic|Catakleismic]][11] in [[72edo|72edo]] (g=19\72 ~ 316.667¢): 4 4 11 4 4 11 4 11 4 4 11
 
[[Orgone|Orgone]][11] in [[26edo|26edo]]: 2 3 2 3 2 2 3 2 2 3 2
 
==[[7L_4s|7L 4s]] aka 7+4==
 
Range: 327.273¢ (3\11edo) to 342.857¢ (2\7edo)
 
Albitonic MOS subsets: [[4L_3s|4L 3s]]
 
[[Amity|Amity]][11]/[[Hitchcock|Hitchcock]][11] in [[46edo|46edo]] (g=13\46 ~ 339.130¢): 1 6 6 1 6 1 6 6 1 6 6
 
==[[3L_8s|3L 8s]] aka 3+8==
 
Range: 400¢ (1\[[3edo|3edo]]) to 436.364¢ (4\11edo)
 
Albitonic MOS subsets: [[3L_5s|3L 5s]]
 
[[Bossier|Bossier]][11] in [[37edo|37edo]] (g=13\37 ~ 431.622¢): 2 2 2 7 2 2 7 2 2 2 7
 
[[Squares|Squares]][11] in [[48edo|48edo]] (g=17\48 = 425¢): 8 3 3 8 3 3 3 8 3 3 3
 
==[[8L_3s|8L 3s]] aka 8+3==
 
Range: 436.364¢ (4\11edo) to 450¢ (3\[[8edo|8edo]])
 
Albitonic MOS subsets: [[3L_5s|3L 5s]]
 
[[Sensi|Sensi]][11] in [[46edo|46edo]] (g=17\46 ~ 443.478¢): 5 5 5 2 5 5 5 2 5 5 2
 
==[[9L_2s|9L 2s]] aka 9+2==
 
Range: 533.333¢ (4\[[9edo|9edo]] to 545.455¢ (5\11edo)
 
Albitonic MOS subsets: [[2L_5s|2L 5s]], [[2L_7s|2L 7s]]
 
[[Avila|Avila]][11] in [[29edo|29edo]] (g=13\29 ~ 537.931¢): 1 3 3 3 3 3 1 3 3 3 3
 
[[casablanca|Casablanca]][11] in [[73edo|73edo]] (g=33\73 ~ 542.466¢): 5 7 7 7 7 7 5 7 7 7 7
 
==[[2L_9s|2L 9s]] aka 2+9==
 
Range: 545.455¢ (5\11edo) to 600¢ (1\[[2edo|2edo]])
 
Albitonic MOS subsets: [[2L_5s|2L 5s]], [[2L_7s|2L 7s]]
 
[[Heinz|Heinz]][11] in [[46edo|46edo]] (g=21\46 ~ 547.826¢): 4 4 4 5 4 4 4 4 4 5 4
 
[[Liese|Liese]][11] in [[74edo|74edo]] (g=35\74 ~ 567.568¢): 4 4 4 19 4 4 4 4 19 4 4
 
[[Triton|Triton]][11] in [[19edo|19edo]] (g=9\19 ~ 568.421¢): 1 1 1 1 5 1 1 1 1 1 5
 
[[Tritonic|Tritonic]][11] in [[60edo|60edo]] (g=29\60 = 580¢): 2 2 2 21 2 2 2 2 2 21 2
[[Category:Lists of scales]]
[[Category:MOS scales]]
[[Category:11-tone scales]]

Latest revision as of 20:20, 23 April 2023

hendecatonic_MOS_scales_PING.png

Hendecatonic (11-tone) MOS Scales come in many varieties and are effective as chromatic scales out of which albitonic (diatonic-like) subsets can be taken. As 11 is a prime number, each Hendecatonic MOS Scale has the octave as a period, rather than some division of the octave like 600¢. It is a simple matter to retune a Halberstadt keyboard to a Hendecatonic MOS Scale, with the 2/1 occurring after 11 keys, or by skipping a key so the 2/1 occurs after 12 keys. The diagram above shows the 10 generator ranges ("Regions") where Hendecatonic MOS Scales occur.

See: chromatic pairs, tridecatonic MOS

The 10 Generator Ranges

1L 10s aka 1+10

Range: 0¢ to 109.091¢ (1\11edo)

Albitonic MOS subsets: 1L 6s, 1L 7s, 1L 8s etc.

Valentine[11] in 46edo (g=3\46 ~ 78.261¢): 3 3 3 3 3 3 3 3 3 16 3

Nautilus[11] in 29edo (g=2\29 ~ 82.759¢): 2 2 2 9 2 2 2 2 2 2

Octacot[11] in 41edo (g=3\41 ~ 88.805¢): 3 3 3 3 3 3 3 3 3 3 11

Passion[11] in 37edo (g=3\37 ~ 97.297¢): 3 3 3 3 3 3 3 3 3 3 7

Ripple[11] in 23edo (g=2\23 ~ 104.348¢): 2 2 2 2 2 2 2 2 2 2 3

10L 1s aka 10+1

Range: 109.091¢ (1\11edo) to 120¢ (1\10edo)

Albitonic MOS subsets: 1L 6s, 1L 7s, 1L 8s etc.

Miracle[11] in 72edo (g=7\72 ~ 116.667¢): 7 7 7 7 7 7 7 2 7 7 7

6L 5s aka 6+5

Range: 200¢ (1\6edo) to 218.182¢ (2\11edo)

Albitonic MOS subsets: 5L 1s

Baldy[11] in 47edo (g=8\47 ~ 204.255¢): 7 1 7 1 7 1 7 7 1 7 1

Machine[11] in 28edo (g=5\28 ~ 214.286¢): 3 2 3 2 3 2 3 3 2 3 2

5L 6s aka 5+6

Range: 218.182¢ (2\11edo) to 240¢ (1\5edo)

Albitonic MOS subsets: 5L 1s

Gorgo[11]/Shoe[11] in 37edo (g=7\37 ~ 227.027¢): 5 2 5 2 5 2 5 2 2 5 2

Cynder[11]/Mothra[11]/Slendric[11] in 31edo (g=6\31 ~ 232.258¢): 1 5 1 5 1 5 1 5 1 1 5

Rodan[11] in 41edo (g=8\41 ~ 234.146¢): 1 7 1 7 1 7 1 7 1 1 7

4L 7s aka 4+7

Range: 300¢ (1\4edo) to 327.273¢ (3\11edo)

Albitonic MOS subsets: 4L 3s

Myna[11] in 89edo: 3 3 17 3 3 17 3 3 17 3 17

Keemun[11]/Hanson[11]/Catakleismic[11] in 72edo (g=19\72 ~ 316.667¢): 4 4 11 4 4 11 4 11 4 4 11

Orgone[11] in 26edo: 2 3 2 3 2 2 3 2 2 3 2

7L 4s aka 7+4

Range: 327.273¢ (3\11edo) to 342.857¢ (2\7edo)

Albitonic MOS subsets: 4L 3s

Amity[11]/Hitchcock[11] in 46edo (g=13\46 ~ 339.130¢): 1 6 6 1 6 1 6 6 1 6 6

3L 8s aka 3+8

Range: 400¢ (1\3edo) to 436.364¢ (4\11edo)

Albitonic MOS subsets: 3L 5s

Bossier[11] in 37edo (g=13\37 ~ 431.622¢): 2 2 2 7 2 2 7 2 2 2 7

Squares[11] in 48edo (g=17\48 = 425¢): 8 3 3 8 3 3 3 8 3 3 3

8L 3s aka 8+3

Range: 436.364¢ (4\11edo) to 450¢ (3\8edo)

Albitonic MOS subsets: 3L 5s

Sensi[11] in 46edo (g=17\46 ~ 443.478¢): 5 5 5 2 5 5 5 2 5 5 2

9L 2s aka 9+2

Range: 533.333¢ (4\9edo to 545.455¢ (5\11edo)

Albitonic MOS subsets: 2L 5s, 2L 7s

Avila[11] in 29edo (g=13\29 ~ 537.931¢): 1 3 3 3 3 3 1 3 3 3 3

Casablanca[11] in 73edo (g=33\73 ~ 542.466¢): 5 7 7 7 7 7 5 7 7 7 7

2L 9s aka 2+9

Range: 545.455¢ (5\11edo) to 600¢ (1\2edo)

Albitonic MOS subsets: 2L 5s, 2L 7s

Heinz[11] in 46edo (g=21\46 ~ 547.826¢): 4 4 4 5 4 4 4 4 4 5 4

Liese[11] in 74edo (g=35\74 ~ 567.568¢): 4 4 4 19 4 4 4 4 19 4 4

Triton[11] in 19edo (g=9\19 ~ 568.421¢): 1 1 1 1 5 1 1 1 1 1 5

Tritonic[11] in 60edo (g=29\60 = 580¢): 2 2 2 21 2 2 2 2 2 21 2

Retrieved from "https://en.xen.wiki/index.php?title=Hendecatonic_MOS&oldid=109003"