16edo

← 15edo

16edo

17edo →

Prime factorization

2⁴

Step size

75 ¢

Fifth

9\16 (675 ¢)

Semitones (A1:m2)

-1:3 (-75 ¢ : 225 ¢)

Dual sharp fifth

10\16 (750 ¢) (→ 5\8)

Dual flat fifth

9\16 (675 ¢)

Dual major 2nd

3\16 (225 ¢)

Consistency limit

7

Distinct consistency limit

5

16 equal divisions of the octave (abbreviated 16edo or 16ed2), also called 16-tone equal temperament (16tet) or 16 equal temperament (16et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 16 equal parts of exactly 75 ¢ each. Each step represents a frequency ratio of 2^1/16, or the 16th root of 2.

16edo's step size is sometimes called an eka, a term proposed by Luca Attanasio, from Sanskrit एक (éka, "one", "unit"),^[1] when used as an interval size unit, especially in the context of Armodue theory.

Theory

The perfect fifth of 16edo is 27 cents flat of 3/2, flatter than that of 7edo so that it generates an antidiatonic instead of diatonic scale, but sharper than 9edo's fifth, to which it similarly retains the characteristic of being a fifth while being distinctly flat of 3/2. If the fifth is interpreted as 3/2, this befits a tuning of mavila, the 5-limit temperament that tempers out 135/128, such that a stack of four fifths gives a 6/5 minor third instead of the familiar 5/4 major third as in meantone. This leads to some confusion in regards to interval names, as what would be major in diatonic now sounds minor; there are several ways to handle this (see in #Intervals).

In general, 16edo tends to better approximate the differences between odd harmonics than odd harmonics themselves, though it has a 5th harmonic which is only 11 cents flat, and a 7th harmonic which is only 6 cents sharp. As such, 16edo can be seen as an approach to tuning that takes advantage of the idea that simpler ratios can be functionally approximated with greater error (i.e. a 3/2 that's 25 cents flat is still recognizable, but a 5/4 that's 25 cents flat loses much of its identity and a 7/4 that's 25 cents flat is completely unrecognizable). In essence, 16edo's 3, 5, and 7 are backwards from 12edo's, with 7 being nearly perfect, 5 being decent, and 3 being distinctly out-of-tune.

In terms of higher primes, both 11 and 13 are approximated very flat, with the 11/8 not distinguished from 4/3, and 13/8 not distinguished from 8/5.

Four steps of 16edo gives the 300 ¢ minor third interval shared by 12edo (and other multiples of 4edo), which approximates 6/5, and thus tempers out 648/625, the diminished comma. This means that the familiar diminished seventh chord may be built on any scale step with four unique tetrads up to octave equivalence. The minor third is of course not distinguished from the septimal subminor third, 7/6, so 36/35 and moreover 50/49 are tempered out, making 16edo a possible tuning for septimal diminished. Another possible interpretation for this interval is the 19th harmonic, 19/16.

16edo shares several similarities with 15edo. They both share mappings of 8/7, 5/4, and 3/2 in terms of edosteps – in fact, they are both valentine tunings, and thus slendric tunings. 16edo and 15edo also both have three types of seconds and two types of thirds (not including arto/tendo thirds). However, 15edo's fifth is sharp while 16's is flat.

16edo works as a tuning for extraclassical tonality, due to its ultramajor third of 450 cents.

Odd harmonics

Approximation of odd harmonics in 16edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-27.0	-11.3	+6.2	+21.1	-26.3	-15.5	+36.7	-30.0	+2.5	-20.8	-28.3
Error	Relative (%)	-35.9	-15.1	+8.2	+28.1	-35.1	-20.7	+49.0	-39.9	+3.3	-27.7	-37.7
Steps (reduced)		25 (9)	37 (5)	45 (13)	51 (3)	55 (7)	59 (11)	63 (15)	65 (1)	68 (4)	70 (6)	72 (8)

Octave stretch

Having a flat tendency, 16et is best tuned with stretched octaves, which improve the accuracy of wide-voiced JI chords and rooted harmonics especially on inharmonic timbres such as bells and gamelans, with 25edt, 41ed6, and 57ed12 being good options.

Subsets and supersets

Since 16 factors into primes as 2⁴, 16edo has subset edos 2, 4, and 8.

Composition theory

Todo: expand

Intervals

This tuning can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways.

The first and most common defines sharp/flat, major/minor and aug/dim in terms of the native antidiatonic scale, such that sharp is higher pitched than flat, and major/aug is wider than minor/dim, as would be expected. Because it does not follow diatonic conventions, conventional interval arithmetic no longer works, e.g. M2 + M2 isn't M3, and D + M2 isn't E. Because antidiatonic is the sister scale to diatonic, you can solve this by swapping major and minor in interval arithmetic rules. Note that the notes that form chords are different from in diatonic: for example, a major chord, P1 – M3 – P5, is approximately 4:5:6 as would be expected, but is notated C-E#-G on C.

Alternatively, one can essentially pretend the native antidiatonic scale is a normal diatonic, meaning that sharp is lower in pitch than flat (since the "S" step is larger than the "L" step) and major/aug is narrower than minor/dim. The primary purpose of doing this is to allow music notated in 12edo or another diatonic system to be directly translated "on the fly" (or to allow support for this tuning in tools that only allow chain-of-fifths notation), and it carries over the way interval arithmetic works from diatonic notation, at the cost of notating the sizes of intervals and the shapes of chords incorrectly: that is, a major chord, P1-M3-P5, is notated C-E-G on C, but is no longer ~4:5:6 (since the third is closer to a minor third).

For the sake of clarity, the first notation is commonly called "melodic notation", and the second is called "harmonic notation", but this is a bit of a misnomer as both preserve different features of the notation of harmony.

Comparison of notations
	P1-M3-P5 ~ 4-5-6	P1-M3-P5 = C-E-G on C
Diatonic notation	No	Yes
Antidiatonic notation	Yes	No

Alternatively, one can use Armodue nine-nominal notation.

Degree	Cents	Approximate ratios*	Names
Degree	Cents	Approximate ratios*	Antidiatonic		Diatonic		Just	Simplified
0	0	1/1	unison	D	unison	D	unison	unison
1	75	28/27, 27/26	aug 1, dim 2nd	D♯, E♭	dim 1, aug 2nd	D♭, E♯	subminor 2nd	min 2nd
2	150	35/32	minor 2nd	E	major 2nd	E	neutral 2nd	maj 2nd
3	225	8/7	major 2nd	E♯	minor 2nd	E♭	supermajor 2nd, septimal whole-tone	perf 2nd
4	300	19/16, 32/27	minor 3rd	F♭	major 3rd	F♯	minor 3rd	min 3rd
5	375	5/4, 16/13, 26/21	major 3rd	F	minor 3rd	F	major 3rd	maj 3rd
6	450	13/10, 35/27	aug 3rd, dim 4th	F♯, G♭	dim 3rd, aug 4th	F♭, G♯	sub-4th, supermajor 3rd	min 4th
7	525	19/14, 27/20, 35/26, 256/189	perfect 4th	G	perfect 4th	G	wide 4th	maj 4th
8	600	7/5, 10/7	aug 4th, dim 5th	G♯, A♭	dim 4th, aug 5th	G♭, A♯	tritone	aug 4th, dim 5th
9	675	28/19, 40/27, 52/35, 189/128	perfect 5th	A	perfect 5th	A	narrow 5th	min 5th
10	750	20/13, 54/35	aug 5th, dim 6th	A♯, B♭	dim 5th, aug 6th	A♭, B♯	super-5th, subminor 6th	maj 5th
11	825	8/5, 13/8, 21/13	minor 6th	B	major 6th	B	minor 6th	min 6th
12	900	27/16, 32/19	major 6th	B♯	minor 6th	B♭	major 6th	maj 6th
13	975	7/4	minor 7th	C♭	major 7th	C♯	subminor 7th, septimal minor 7th	perf 7th
14	1050	64/35	major 7th	C	minor 7th	C	neutral 7th	min 7th
15	1125	27/14, 52/27	aug 7th, dim 8ve	C♯, D♭	dim 7th, aug 8ve	C♭, D♯	supermajor 7th	maj 7th
16	1200	2/1	8ve	D	8ve	D	octave	octave

* Based on treating 16edo as a 2.5.7.13.19.27 subgroup temperament; other approaches are possible.

Notation

16edo notation can be easy utilizing Goldsmith's Circle of keys, nominals, and respective notation^{[clarification needed]}. The nominals for a 6 line staff can be switched for Erv Wilson's Beta and Epsilon additions to A–G. The Armodue model uses a 4-line staff for 16edo.

Mos scales like Mavila[7] (or "inverse/anti-diatonic" which reverses step sizes of diatonic from LLsLLLs to ssLsssL in the heptatonic variation) can work as an alternative to the traditional diatonic scale, while maintaining conventional A–G ♯/♭ notation as described above. Alternatively, one can utilize the Mavila[9] mos, for a sort of "hyper-diatonic" scale of 7 large steps and 2 small steps. Armodue notation of 16edo "Mavila[9] Staff" does just this, and places the arrangement (222122221) on nine white "natural" keys of the 16edo keyboard. If the 9-note (enneatonic) mos is adopted as a notational basis for 16edo, then we need an entirely different set of interval classes than any of the heptatonic classes described above; perhaps it even makes sense to refer to the octave (2/1) as the "decave". This is identical to the KISS notation for this scale when using numbers.

Degree	Cents	Mavila[9] notation
0	0	unison	1
1	75	aug unison, minor 2nd	1♯, 2♭
2	150	major 2nd	2
3	225	aug 2nd, minor 3rd	2♯, 3♭
4	300	major 3rd, dim 4th	3, 4𝄫
5	375	minor 4th	4♭
6	450	major 4th, dim 5th	4, 5♭
7	525	aug 4th, minor 5th	4♯, 5
8	600	aug 5th, dim 6th	5♯, 6♭
9	675	perfect 6th, dim 7th	6, 7𝄫
10	750	aug 6th, minor 7th	6♯, 7♭
11	825	major 7th	7
12	900	aug 7th, minor 8th	7♯, 8♭
13	975	major 8th, dim 9th	8, 9𝄫
14	1050	minor 9th	9
15	1125	major 9th, dim 10ve	9♯, 1♭
16	1200	10ve (Decave)	1

Sagittal notation

This notation uses the same sagittal sequence as 21edo.

Armodue notation (4-line staff)

Armodue: Pierpaolo Beretta's website for his Armodue theory for 16edo (esadekaphonic), including compositions.

For resources on the Armodue theory, see the Armodue on this wiki

Chord names

16edo chords can be named using ups and downs. Using diatonic interval names, chord names bear little relationship to the sound: a minor chord (spelled A – C – E) sounds like 4:5:6, the classical major triad, and a major chord (spelled C – E – G) sounds like 10:12:15, a classical minor triad! Instead, using antidiatonic names, the chord names will match the sound—but finding the name from the spelling follows the rules of antidiatonic rather than diatonic interval arithmetic.

Chord	JI ratios	Name
Chord	JI ratios	Diatonic			Antidiatonic
0 – 5 – 9	4:5:6	D F A	Dm	D minor	D F A	D	D major
0 – 4 – 9	10:12:15	D F♯ A	D	D major	D F♭ A	Dm	D minor
0 – 4 – 8	5:6:7	D F♯ A♯	Daug	D augmented	D F♭ A♭	Ddim	D diminished
0 – 5 – 10		D F A♭	Ddim	D diminished	D F A♯	Daug	D augmented
0 – 5 – 9 – 13	4:5:6:7	D F A C♯	Dm(M7)	D minor-major	D F A C♭	D7	D seven
0 – 5 – 9 – 12		D F A Bb	Dm(♭6)	D minor flat-six	D F A B♯	D6	D six
0 – 5 – 9 – 14		D F A C	Dm7	D minor seven	D F A C	DM7	D major seven
0 – 4 – 9 – 13		D F♯ A C♯	DM7	D major seven	D F♭ A C♭	DM7	D minor seven

Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6 – 1 – 3 – 5 – 7 – 9 – 11 – 13). See Ups and downs notation #Chords and chord progressions for more examples.

Using antidiatonic names, if you're used to diatonic interval arithmetic, you can do antidiatonic interval arithmetic by following the simple guideline that qualities are reversed from standard diatonic. As in, just as adding two major seconds gives you a major third in 12edo, adding two minor seconds gives a minor third in 16edo.

That is, reversing means exchanging major for minor, aug for dim, and sharp for flat. Perfect and natural are unaffected.

Examples can be found at the bottom of the page.

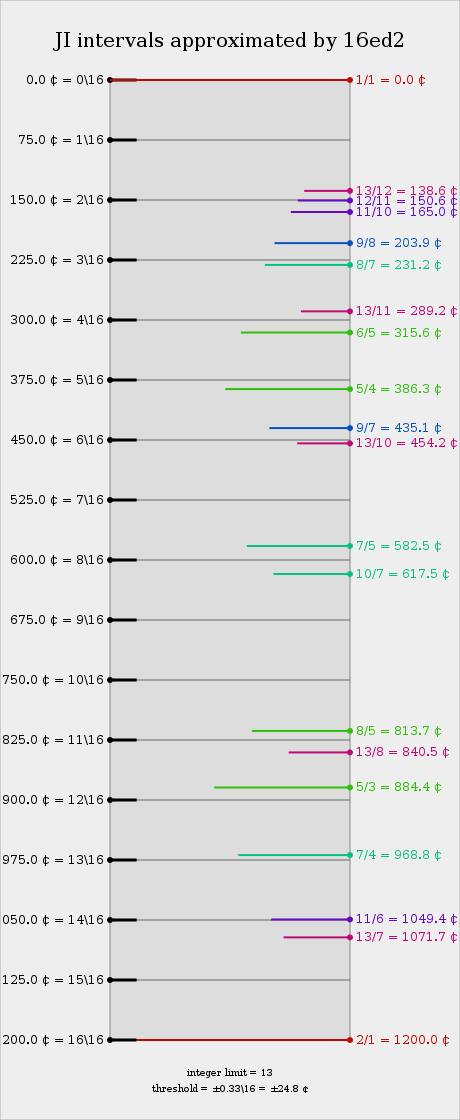
Approximation to JI

Selected just intervals by error

The following tables show how 15-odd-limit intervals are represented in 16edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 16edo (direct approximation, even if inconsistent)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
11/6, 12/11	0.637	0.8
13/10, 20/13	4.214	5.6
7/4, 8/7	6.174	8.2
13/11, 22/13	10.790	14.4
5/4, 8/5	11.314	15.1
13/12, 24/13	11.427	15.2
15/11, 22/15	11.951	15.9
9/7, 14/9	14.916	19.9
11/10, 20/11	15.004	20.0
13/8, 16/13	15.528	20.7
5/3, 6/5	15.641	20.9
7/5, 10/7	17.488	23.3
9/8, 16/9	21.090	28.1
13/7, 14/13	21.702	28.9
15/13, 26/15	22.741	30.3
11/8, 16/11	26.318	35.1
3/2, 4/3	26.955	35.9
11/9, 18/11	27.592	36.8
15/14, 28/15	30.557	40.7
9/5, 10/9	32.404	43.2
11/7, 14/11	32.492	43.3
7/6, 12/7	33.129	44.2
13/9, 18/13	36.618	48.8
15/8, 16/15	36.731	49.0

15-odd-limit intervals in 16edo (patent val mapping)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
11/6, 12/11	0.637	0.8
13/10, 20/13	4.214	5.6
7/4, 8/7	6.174	8.2
13/11, 22/13	10.790	14.4
5/4, 8/5	11.314	15.1
13/12, 24/13	11.427	15.2
15/11, 22/15	11.951	15.9
11/10, 20/11	15.004	20.0
13/8, 16/13	15.528	20.7
5/3, 6/5	15.641	20.9
7/5, 10/7	17.488	23.3
13/7, 14/13	21.702	28.9
15/13, 26/15	22.741	30.3
11/8, 16/11	26.318	35.1
3/2, 4/3	26.955	35.9
11/9, 18/11	27.592	36.8
11/7, 14/11	32.492	43.3
7/6, 12/7	33.129	44.2
15/8, 16/15	38.269	51.0
13/9, 18/13	38.382	51.2
9/5, 10/9	42.596	56.8
15/14, 28/15	44.443	59.3
9/8, 16/9	53.910	71.9
9/7, 14/9	60.084	80.1

It's worth noting that the 525 ¢ interval is almost exactly halfway in between 4/3 and 11/8, making it very discordant, although playing this in the context of a larger chord, and with specialized timbres, can make this less noticeable.

16ed2-001.svg

Zeta peak index

Tuning			Strength				Octave (cents)		Integer limit
ZPI	Steps per 8ve	Step size (cents)	Height		Integral	Gap	Size	Stretch	Consistent	Distinct
ZPI	Steps per 8ve	Step size (cents)	Tempered	Pure	Integral	Gap	Size	Stretch	Consistent	Distinct
51zpi	15.944373	75.26166	4.191572	3.476281	0.812082	13.070433	1204.186562	4.186562	6	6

Octave theory

The scale supports the diminished temperament with its 1/4 octave period, though its generator size, equal to its step size of 75 ¢, is smaller than ideal. Its very flat 3/2 of 675 ¢ supports Mavila temperament, where the mapping of major and minor is reversed. The temperament could be popular for its 150 ¢ "3/4-tone" equal division of the traditional 300 ¢ minor third.

16edo is also a tuning for the no-threes 7-limit temperament tempering out 50/49. This has a period of a half-octave (600 ¢), and a generator of a flat septimal major 2nd, for which 16edo uses 3\16. For this, there are mos scales of sizes 4, 6, and 10; extending this temperament to the full 7-limit can produce either Lemba or Astrology (16edo supports both, but is not a very accurate tuning of either).

16edo is also a tuning for the no-threes 7-limit temperament tempering out 546875:524288, which has a flat major third as generator, for which 16-EDO provides 5\16 octaves. For this, there are MOS of sizes 7, 10, and 13; these are shown below under "Magic family of scales".

Easley Blackwood Jr writes of 16edo:

"16 notes: This tuning is best thought of as a combination of four intertwined diminished seventh chords. Since 12-note tuning can be regarded as a combination of three diminished seventh chords, it is plain that the two tunings have elements in common. The most obvious difference in the way the two tunings sound and work is that triads in 16-note tuning, although recognizable, are too discordant to serve as the final harmony in cadences. Keys can still be established by successions of altered subdominant and dominant harmonies, however, and the Etude is based mainly upon this property. The fundamental consonant harmony employed is a minor triad with an added minor seventh."

From a harmonic series perspective, if we take 13\16 as a 7/4 ratio approximation, sharp by 6.174 ¢, and take the 300 ¢ minor third as an approximation of the harmonic 19th (19/16, approximately 297.5 ¢), that can combine with the approximation of the harmonic seventh to form a 16:19:28 triad .

The interval between the 28th & 19th harmonics, 28:19, measures approximately 671.3 ¢, which is 3.7 ¢ away from 16edo's "narrow fifth". Another voicing for this chord is 14:16:19, which features 19:14 as the outer interval (528.7 ¢ just, 525.0 ¢ in 16edo). A perhaps more consonant open voicing is 7:16:19

Regular temperament properties

Uniform maps

13-limit uniform maps between 15.8 and 16.2
Min. size	Max. size	Wart notation	Map
15.7540	15.8089	16dff	⟨16 25 37 44 55 58]
15.8089	15.8512	16d	⟨16 25 37 44 55 59]
15.8512	16.0431	16	⟨16 25 37 45 55 59]
16.0431	16.0792	16e	⟨16 25 37 45 56 59]
16.0792	16.0887	16ef	⟨16 25 37 45 56 60]
16.0887	16.1504	16bef	⟨16 26 37 45 56 60]
16.1504	16.2074	16bcef	⟨16 26 38 45 56 60]

Commas

16et tempers out the following commas. (Note: This assumes val ⟨16 25 37 45 55 59].)

Prime limit	Ratio^{[note 1]}	Monzo	Cents	Color name	Name
5	135/128	[-7 3 1⟩	92.18	Layobi	Mavila comma, major chroma
5	648/625	[3 4 -4⟩	62.57	Quadgu	Diminished comma, major diesis
5	3125/3072	[-10 -1 5⟩	29.61	Laquinyo	Magic comma
5	(20 digits)	[23 6 -14⟩	3.34	Sasepbiru	Vishnuzma
7	36/35	[2 2 -1 -1⟩	48.77	Rugu	Mint comma, septimal quartertone
7	525/512	[-9 1 2 1⟩	43.41	Lazoyoyo	Avicennma
7	50/49	[1 0 2 -2⟩	34.98	Biruyo	Jubilisma
7	64827/64000	[-9 3 -3 4⟩	22.23	Laquadzo-atrigu	Squalentine comma
7	3125/3087	[0 -2 5 -3⟩	21.18	Triru-aquinyo	Gariboh comma
7	126/125	[1 2 -3 1⟩	13.79	Zotrigu	Starling comma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	6144/6125	[11 1 -3 -2⟩	5.36	Sarurutrigu	Porwell comma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	441/440	[-3 2 -1 2 -1⟩	3.93	Luzozogu	Werckisma
11	3025/3024	[-4 -3 2 -1 2⟩	0.57	Loloruyoyo	Lehmerisma

Rank-2 temperaments

List of 16et rank two temperaments by badness

Table of temperaments by generator
Periods per 8ve	Generator	Temperaments
1	1\16	Valentine, slurpee
1	3\16	Gorgo
1	5\16	Magic/muggles
1	7\16	Mavila/armodue
2	1\16	Bipelog
2	3\16	Lemba, astrology
4	1\16	Diminished/demolished
8	1\16	Semidim

Scales

Main article: List of MOS scales in 16edo

Important mosses include:

magic anti-diatonic 3L4s 1414141 (5\16, 1\1)
magic superdiatonic 3L7s 1311311311 (5\16, 1\1)
magic chromatic 11121121112 3L10s (5\16, 1\1)
mavila anti-diatonic 2L5s 2223223 (9\16, 1\1)
mavila superdiatonic 7L2s 222212221 (9\16, 1\1)
gorgo 5L1s 333331 (3\16, 1\1)
lemba 4L2s 332332 (3\16, 1\2)

Mavila

[5]:	5 2 5 2 2
[7]:	3 2 2 3 2 2 2
[9]:	1 2 2 2 1 2 2 2 2

Diminished

[8]:	1 3 1 3 1 3 1 3
[12]:	1 1 2 1 1 2 1 1 2 1 1 2

Magic

[7]: 1 4 1 4 1 4 1

[10]: 1 3 1 1 3 1 1 1 3 1

[13]: 1 1 2 1 1 1 2 1 1 1 2 1 1

Cynder/Gorgo

[5]: 3 3 4 3 3

[6]: 3 3 1 3 3 3

[11]: 1 2 1 2 1 2 1 2 1 2 1

Lemba/Astrology

[4]: 3 5 3 5

[6]: 3 2 3 3 2 3

[10]: 2 1 2 1 2 2 1 2 1 2

Metallic harmony

In 16edo, triadic harmony can be based on on heptatonic sevenths (or seconds) rather than thirds. For instance, 16edo approximates 7/4 well enough to use

it in place of the usual 3/2, and in Mavila[7] this 7/4 approximation shares an interval class with a well-approximated 11/6 (at 1050 ¢). Stacking these two intervals reaches 2025 ¢, or a minor 6th plus an octave. Thus the out-of-tune 675 ¢ interval is bypassed, and all the dyads in the triad are consonant.

Depending on whether the Mavila[7] major 7th or minor 7th is used, one of two triads is produced: a small one, 0 – 975 – 2025 ¢, and a large one, 0 – 1050 – 2025 ¢. William Lynch, a major proponent of this style of harmony, calls these two triads "hard" and "soft", respectively. In addition, two other "symmetrical" triads are also obvious possible chords: a narrow symmetrical triad at 0 – 975 – 1950 ¢, and a wide symmetrical triad at 0 – 1050 – 2100 ¢. These are sort of analogous to "diminished" and "augmented" triads. The characteristic buzzy/metallic sound of these seventh-based triads inspired William Lynch to call them "Metallic triads".

MOS scales supporting metallic harmony in 16edo

The ssLsssL mode of Mavila[7] contains two hard triads on degrees 1 and 4 and two soft triads on degrees 2 and 6. The other three chords are wide symmetrical triads 0-1050-2025 ¢. In Mavila[9], hard and soft triads cease to share a triad class, as 975 ¢ is a major 8th, while 1050 ¢ is a minor 9th; the triads may still be used, but parallel harmonic motion will function differently.

Another possible MOS scales for this approach would be Lemba[6], which gives two each of the soft, hard, and narrow symmetric triads.

See: Metallic Harmony.

Diagrams

16-tone piano layout based on the mavila[7]/antidiatonic scale

This Layout places mavila[7] on the black keys and mavila[9] on the white keys, according to antidiatonic notation.

Un-annotated diagram

Please explain this image.

Lumatone mapping

See: Lumatone mapping for 16edo

Interval arithmetic examples

These examples show the correspondence between interval arithmetic using diatonic and antidiatonic notation.

Diatonic (i.e. 12edo)		Antidiatonic (i.e. 16edo)
Question	Result	Question	Result
M2 + M2	aug3	m2 + m2	dim3
D to F♯	aug3	D to F♭	dim3
D to F	M3	D to F	m3
E♭ + m3	Gbb	E♯ + M3	G♯♯
E♭ + P5	B♭	E♯ + P5	B♯
A minor chord	A C♭ E	A major chord	A C♯ E
E♭ major chord	E♭ G♭ D♭	E♯ minor chord	E♯ G♯ B♯
Gm7 = G + m3 + P5 + m7	G B D F♭	G + M3 + P5 + M7	G B D F♯
A♭7aug = A♭ + M3 + A5 + m7	A♭ C♭ E Gbb	A♯ + m3 + d5 + M7	A♯ C♯ E G♯♯
what chord is D F A♯?	D + M3 + A5 = Daug	D F A♭	D + m3 + d5
what chord is C E G♭ B♭?	C + m3 + d5 + d7 = Cdim7	C E G♯ B♯	C + M3 + A5 + A7
C major scale = C + M2 + M3 + P4 + P5 + M6 + M7 + P8	C D♯ E♯ F G A♯ B♯ C	C + m2 + m3 + P4 + P5 + m6 + m7 + P8	C D♭ E♭ F G A♭ B♭ C
C minor scale = C + M2 + m3 + P4 + P5 + m6 + m7 + P8	C D♯ E F G A B C	C + m2 + M3 + P4 + P5 + M6 + M7 + P8	C D♭ E F G A B C
what scale is A B♯ C♭ D E F G♭ A?	A + M2 + m3 + P4 + P5 + M6 + m7 = A dorian	A B♭ C♯ D E F G♯ A	A + m2 + M3 + P4 + P5 + m6 + M7