16edo
| ← 15edo | 16edo | 17edo → |
16 equal divisions of the octave (abbreviated 16edo or 16ed2), also called 16-tone equal temperament (16tet) or 16 equal temperament (16et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 16 equal parts of exactly 75 ¢ each. Each step represents a frequency ratio of 21/16, or the 16th root of 2.
16edo's step size is sometimes called an eka, a term proposed by Luca Attanasio, from Sanskrit एक (éka, "one", "unit"),[1] when used as an interval size unit, especially in the context of Armodue theory.
Theory
The perfect fifth of 16edo is 27 cents flat of 3/2, flatter than that of 7edo so that it generates an antidiatonic instead of diatonic scale, but sharper than 9edo's fifth, to which it similarly retains the characteristic of being a fifth while being distinctly flat of 3/2. If the fifth is interpreted as 3/2, this befits a tuning of mavila, the 5-limit temperament that tempers out 135/128, such that a stack of four fifths gives a 6/5 minor third instead of the familiar 5/4 major third as in meantone. A more accurate restriction is mabilic, which discards the inaccurate mapping of 3 while keeping the fifth as a generator.
This leads to some confusion in regards to interval names, as what would be major in diatonic now sounds minor; there are several ways to handle this (see in #Intervals).
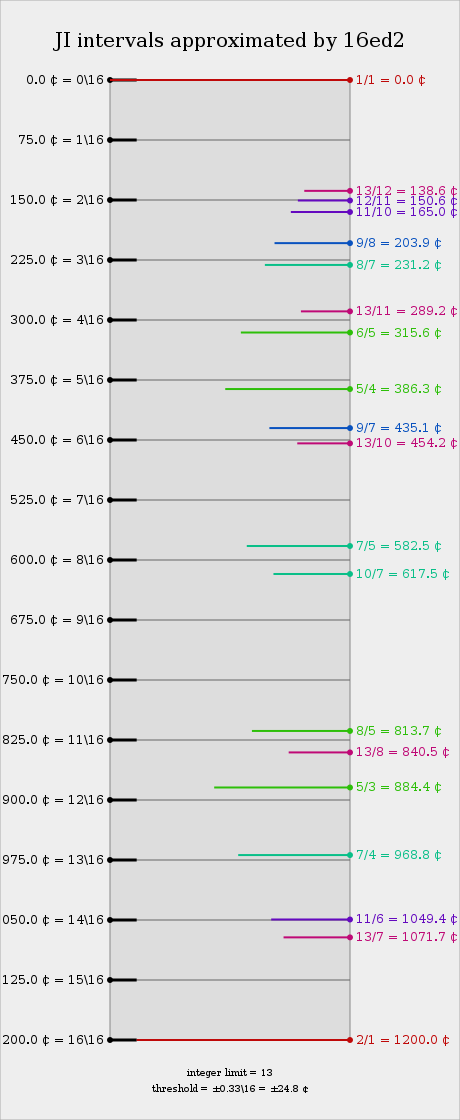
In general, 16edo tends to better approximate the differences between odd harmonics than odd harmonics themselves, though it has a 5th harmonic which is only 11 cents flat, and a 7th harmonic which is only 6 cents sharp. As such, 16edo can be seen as an approach to tuning that takes advantage of the idea that simpler ratios can be functionally approximated with greater error (i.e. a 3/2 that's 25 cents flat is still recognizable, but a 5/4 that's 25 cents flat loses much of its identity and a 7/4 that's 25 cents flat is completely unrecognizable). In essence, 16edo's 3, 5, and 7 are backwards from 12edo's, with 7 being nearly perfect, 5 being decent, and 3 being distinctly out-of-tune.
In terms of higher primes, both 11 and 13 are approximated very flat, with the 11/8 not distinguished from 4/3, and 13/8 not distinguished from 8/5. 16edo represents the no-9 no-15 25-odd-limit consistently, however.
Four steps of 16edo gives the 300 ¢ minor third interval shared by 12edo (and other multiples of 4edo), which approximates 6/5, and thus tempers out 648/625, the diminished comma. This means that the familiar diminished seventh chord may be built on any scale step with four unique tetrads up to octave equivalence. The minor third is of course not distinguished from the septimal subminor third, 7/6, so 36/35 and moreover 50/49 are tempered out, making 16edo a possible tuning for septimal diminished. Another possible interpretation for this interval is the 19th harmonic, 19/16.
16edo shares several similarities with 15edo. They both share mappings of 8/7, 5/4, and 3/2 in terms of edosteps – in fact, they are both valentine tunings, and thus slendric tunings. 16edo and 15edo also both have three types of seconds and two types of thirds (not including arto/tendo thirds). However, 15edo's fifth is sharp while 16's is flat.
16edo works as a tuning for extraclassical tonality, due to its ultramajor third of 450 cents.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -27.0 | -11.3 | +6.2 | +21.1 | -26.3 | -15.5 | +36.7 | -30.0 | +2.5 | -20.8 | -28.3 |
| Relative (%) | -35.9 | -15.1 | +8.2 | +28.1 | -35.1 | -20.7 | +49.0 | -39.9 | +3.3 | -27.7 | -37.7 | |
| Steps (reduced) |
25 (9) |
37 (5) |
45 (13) |
51 (3) |
55 (7) |
59 (11) |
63 (15) |
65 (1) |
68 (4) |
70 (6) |
72 (8) | |
Subsets and supersets
Since 16 factors into primes as 24, 16edo has subset edos 2, 4, and 8.
Composition theory
Intervals
16edo can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways.
The first, melodic notation, defines sharp/flat, major/minor, and aug/dim in terms of the antidiatonic scale, such that sharp is higher pitched than flat, and major/aug is wider than minor/dim, as would be expected. Because it does not follow diatonic conventions, conventional interval arithmetic no longer works, e.g. M2 + M2 is not M3, and D + M2 is not E. Because antidiatonic is the sister scale to diatonic, you can solve this by swapping major and minor in interval arithmetic rules. Note that the notes that form chords are different from in diatonic: for example, a major chord, P1–M3–P5, is approximately 4:5:6 as would be expected, but is notated C–E♯–G on C.
Alternatively, one can essentially pretend the antidiatonic scale is a normal diatonic, meaning that sharp is lower in pitch than flat (since the "S" step is larger than the "L" step) and major/aug is narrower than minor/dim, known as harmonic notation. The primary purpose of doing this is to allow music notated in 12edo or another diatonic system to be directly translated on the fly, or to allow support for 16edo in tools that only allow chain-of-fifths notation, and it carries over the way interval arithmetic works from diatonic notation, at the cost of notating the sizes of intervals and the shapes of chords incorrectly: that is, a major chord, P1–M3–P5, is notated C–E–G on C, but is no longer ~4:5:6 (since the third is closer to a minor third).
For the sake of clarity, the first notation is commonly called melodic notation, and the second is called harmonic notation, but this is a bit of a misnomer as both preserve different features of the notation of harmony.
| Notation | P1–M3–P5 ~ 4:5:6 | P1–M3–P5 = C–E–G on C |
|---|---|---|
| Diatonic | No | Yes |
| Antidiatonic | Yes | No |
Alternatively, one can use Armodue nine-nominal notation.
| Degree | Cents | Approximate ratios* |
Names | |||||
|---|---|---|---|---|---|---|---|---|
| Antidiatonic | Diatonic | Just | Simplified | |||||
| 0 | 0 | 1/1 | unison | D | unison | D | unison | unison |
| 1 | 75 | 28/27, 27/26 | aug 1, dim 2nd | D♯, E♭ | dim 1, aug 2nd | D♭, E♯ | subminor 2nd | min 2nd |
| 2 | 150 | 35/32 | minor 2nd | E | major 2nd | E | neutral 2nd | maj 2nd |
| 3 | 225 | 8/7 | major 2nd | E♯ | minor 2nd | E♭ | supermajor 2nd, septimal whole-tone |
perf 2nd |
| 4 | 300 | 19/16, 32/27 | minor 3rd | F♭ | major 3rd | F♯ | minor 3rd | min 3rd |
| 5 | 375 | 5/4, 16/13, 26/21 | major 3rd | F | minor 3rd | F | major 3rd | maj 3rd |
| 6 | 450 | 13/10, 35/27 | aug 3rd, dim 4th |
F♯, G♭ | dim 3rd, aug 4th |
F♭, G♯ | sub-4th, supermajor 3rd |
min 4th |
| 7 | 525 | 19/14, 27/20, 35/26, 256/189 | perfect 4th | G | perfect 4th | G | wide 4th | maj 4th |
| 8 | 600 | 7/5, 10/7 | aug 4th, dim 5th |
G♯, A♭ | dim 4th, aug 5th |
G♭, A♯ | tritone | aug 4th, dim 5th |
| 9 | 675 | 28/19, 40/27, 52/35, 189/128 | perfect 5th | A | perfect 5th | A | narrow 5th | min 5th |
| 10 | 750 | 20/13, 54/35 | aug 5th, dim 6th |
A♯, B♭ | dim 5th, aug 6th |
A♭, B♯ | super-5th, subminor 6th |
maj 5th |
| 11 | 825 | 8/5, 13/8, 21/13 | minor 6th | B | major 6th | B | minor 6th | min 6th |
| 12 | 900 | 27/16, 32/19 | major 6th | B♯ | minor 6th | B♭ | major 6th | maj 6th |
| 13 | 975 | 7/4 | minor 7th | C♭ | major 7th | C♯ | subminor 7th, septimal minor 7th |
perf 7th |
| 14 | 1050 | 64/35 | major 7th | C | minor 7th | C | neutral 7th | min 7th |
| 15 | 1125 | 27/14, 52/27 | aug 7th, dim 8ve |
C♯, D♭ | dim 7th, aug 8ve |
C♭, D♯ | supermajor 7th | maj 7th |
| 16 | 1200 | 2/1 | 8ve | D | 8ve | D | octave | octave |
* Based on treating 16edo as a 2.5.7.13.19.27 subgroup temperament; other approaches are possible.
Notation
16edo notation can be easy utilizing Goldsmith's Circle of keys, nominals, and respective notation[clarification needed]. The nominals for a 6 line staff can be switched for Erv Wilson's Beta and Epsilon additions to A–G. The Armodue model uses a 4-line staff for 16edo.
Mos scales like Mavila[7] (or "inverse/anti-diatonic" which reverses step sizes of diatonic from LLsLLLs to ssLsssL in the heptatonic variation) can work as an alternative to the traditional diatonic scale, while maintaining conventional A–G ♯/♭ notation as described above. Alternatively, one can utilize the Mavila[9] mos, for a sort of "hyper-diatonic" scale of 7 large steps and 2 small steps. Armodue notation of 16edo "Mavila[9] Staff" does just this, and places the arrangement (222122221) on nine white "natural" keys of the 16edo keyboard. If the 9-note (enneatonic) mos is adopted as a notational basis for 16edo, then we need an entirely different set of interval classes than any of the heptatonic classes described above; perhaps it even makes sense to refer to the octave (2/1) as the "decave". This is identical to the KISS notation for this scale when using numbers.
| Degree | Cents | Mavila[9] notation | |
|---|---|---|---|
| 0 | 0 | unison | 1 |
| 1 | 75 | aug unison, minor 2nd | 1♯, 2♭ |
| 2 | 150 | major 2nd | 2 |
| 3 | 225 | aug 2nd, minor 3rd | 2♯, 3♭ |
| 4 | 300 | major 3rd, dim 4th | 3, 4𝄫 |
| 5 | 375 | minor 4th | 4♭ |
| 6 | 450 | major 4th, dim 5th |
4, 5♭ |
| 7 | 525 | aug 4th, minor 5th | 4♯, 5 |
| 8 | 600 | aug 5th, dim 6th | 5♯, 6♭ |
| 9 | 675 | perfect 6th, dim 7th | 6, 7𝄫 |
| 10 | 750 | aug 6th, minor 7th | 6♯, 7♭ |
| 11 | 825 | major 7th | 7 |
| 12 | 900 | aug 7th, minor 8th | 7♯, 8♭ |
| 13 | 975 | major 8th, dim 9th | 8, 9𝄫 |
| 14 | 1050 | minor 9th | 9 |
| 15 | 1125 | major 9th, dim 10ve | 9♯, 1♭ |
| 16 | 1200 | 10ve (Decave) | 1 |
Sagittal notation
This notation uses the same sagittal sequence as 21edo.

Armodue notation (4-line staff)
Armodue: Pierpaolo Beretta's website for his Armodue theory for 16edo (esadekaphonic), including compositions.
For resources on the Armodue theory, see the Armodue on this wiki
Chord names
16edo chords can be named using ups and downs. Using diatonic interval names, chord names bear little relationship to the sound: a minor chord (spelled A – C – E) sounds like 4:5:6, the classical major triad, and a major chord (spelled C – E – G) sounds like 10:12:15, a classical minor triad! Instead, using antidiatonic names, the chord names will match the sound—but finding the name from the spelling follows the rules of antidiatonic rather than diatonic interval arithmetic.
| Chord | JI ratios | Name | |||||
|---|---|---|---|---|---|---|---|
| Diatonic | Antidiatonic | ||||||
| 0 – 5 – 9 | 4:5:6 | D F A | Dm | D minor | D F A | D | D major |
| 0 – 4 – 9 | 10:12:15 | D F♯ A | D | D major | D F♭ A | Dm | D minor |
| 0 – 4 – 8 | 5:6:7 | D F♯ A♯ | Daug | D augmented | D F♭ A♭ | Ddim | D diminished |
| 0 – 5 – 10 | D F A♭ | Ddim | D diminished | D F A♯ | Daug | D augmented | |
| 0 – 5 – 9 – 13 | 4:5:6:7 | D F A C♯ | Dm(M7) | D minor-major | D F A C♭ | D7 | D seven |
| 0 – 5 – 9 – 12 | D F A Bb | Dm(♭6) | D minor flat-six | D F A B♯ | D6 | D six | |
| 0 – 5 – 9 – 14 | D F A C | Dm7 | D minor seven | D F A C | DM7 | D major seven | |
| 0 – 4 – 9 – 13 | D F♯ A C♯ | DM7 | D major seven | D F♭ A C♭ | DM7 | D minor seven | |
Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6 – 1 – 3 – 5 – 7 – 9 – 11 – 13). See Ups and downs notation #Chords and chord progressions for more examples.
Using antidiatonic names, if you're used to diatonic interval arithmetic, you can do antidiatonic interval arithmetic by following the simple guideline that qualities are reversed from standard diatonic. As in, just as adding two major seconds gives you a major third in 12edo, adding two minor seconds gives a minor third in 16edo.
That is, reversing means exchanging major for minor, aug for dim, and sharp for flat. Perfect and natural are unaffected.
Examples can be found at the bottom of the page.
Approximation to JI
Selected just intervals by error
The following tables show how 15-odd-limit intervals are represented in 16edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/6, 12/11 | 0.637 | 0.8 |
| 13/10, 20/13 | 4.214 | 5.6 |
| 7/4, 8/7 | 6.174 | 8.2 |
| 13/11, 22/13 | 10.790 | 14.4 |
| 5/4, 8/5 | 11.314 | 15.1 |
| 13/12, 24/13 | 11.427 | 15.2 |
| 15/11, 22/15 | 11.951 | 15.9 |
| 9/7, 14/9 | 14.916 | 19.9 |
| 11/10, 20/11 | 15.004 | 20.0 |
| 13/8, 16/13 | 15.528 | 20.7 |
| 5/3, 6/5 | 15.641 | 20.9 |
| 7/5, 10/7 | 17.488 | 23.3 |
| 9/8, 16/9 | 21.090 | 28.1 |
| 13/7, 14/13 | 21.702 | 28.9 |
| 15/13, 26/15 | 22.741 | 30.3 |
| 11/8, 16/11 | 26.318 | 35.1 |
| 3/2, 4/3 | 26.955 | 35.9 |
| 11/9, 18/11 | 27.592 | 36.8 |
| 15/14, 28/15 | 30.557 | 40.7 |
| 9/5, 10/9 | 32.404 | 43.2 |
| 11/7, 14/11 | 32.492 | 43.3 |
| 7/6, 12/7 | 33.129 | 44.2 |
| 13/9, 18/13 | 36.618 | 48.8 |
| 15/8, 16/15 | 36.731 | 49.0 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/6, 12/11 | 0.637 | 0.8 |
| 13/10, 20/13 | 4.214 | 5.6 |
| 7/4, 8/7 | 6.174 | 8.2 |
| 13/11, 22/13 | 10.790 | 14.4 |
| 5/4, 8/5 | 11.314 | 15.1 |
| 13/12, 24/13 | 11.427 | 15.2 |
| 15/11, 22/15 | 11.951 | 15.9 |
| 11/10, 20/11 | 15.004 | 20.0 |
| 13/8, 16/13 | 15.528 | 20.7 |
| 5/3, 6/5 | 15.641 | 20.9 |
| 7/5, 10/7 | 17.488 | 23.3 |
| 13/7, 14/13 | 21.702 | 28.9 |
| 15/13, 26/15 | 22.741 | 30.3 |
| 11/8, 16/11 | 26.318 | 35.1 |
| 3/2, 4/3 | 26.955 | 35.9 |
| 11/9, 18/11 | 27.592 | 36.8 |
| 11/7, 14/11 | 32.492 | 43.3 |
| 7/6, 12/7 | 33.129 | 44.2 |
| 15/8, 16/15 | 38.269 | 51.0 |
| 13/9, 18/13 | 38.382 | 51.2 |
| 9/5, 10/9 | 42.596 | 56.8 |
| 15/14, 28/15 | 44.443 | 59.3 |
| 9/8, 16/9 | 53.910 | 71.9 |
| 9/7, 14/9 | 60.084 | 80.1 |
It's worth noting that the 525 ¢ interval is almost exactly halfway in between 4/3 and 11/8, making it very discordant, although playing this in the context of a larger chord, and with specialized timbres, can make this less noticeable.
Octave theory
The scale supports the diminished temperament with its 1/4 octave period, though its generator size, equal to its step size of 75 ¢, is smaller than ideal. Its very flat 3/2 of 675 ¢ supports Mavila temperament, where the mapping of major and minor is reversed. The temperament could be popular for its 150 ¢ "3/4-tone" equal division of the traditional 300 ¢ minor third.
16edo is also a tuning for the no-threes 7-limit temperament tempering out 50/49. This has a period of a half-octave (600 ¢), and a generator of a flat septimal major 2nd, for which 16edo uses 3\16. For this, there are mos scales of sizes 4, 6, and 10; extending this temperament to the full 7-limit can produce either Lemba or Astrology (16edo supports both, but is not a very accurate tuning of either).
16edo is also a tuning for the no-threes 7-limit temperament tempering out 546875:524288, which has a flat major third as generator, for which 16-EDO provides 5\16 octaves. For this, there are MOS of sizes 7, 10, and 13; these are shown below under "Magic family of scales".
Easley Blackwood Jr writes of 16edo:
"16 notes: This tuning is best thought of as a combination of four intertwined diminished seventh chords. Since 12-note tuning can be regarded as a combination of three diminished seventh chords, it is plain that the two tunings have elements in common. The most obvious difference in the way the two tunings sound and work is that triads in 16-note tuning, although recognizable, are too discordant to serve as the final harmony in cadences. Keys can still be established by successions of altered subdominant and dominant harmonies, however, and the Etude is based mainly upon this property. The fundamental consonant harmony employed is a minor triad with an added minor seventh."
From a harmonic series perspective, if we take 13\16 as a 7/4 ratio approximation, sharp by 6.174 ¢, and take the 300 ¢ minor third as an approximation of the harmonic 19th (19/16, approximately 297.5 ¢), that can combine with the approximation of the harmonic seventh to form a 16:19:28 triad .
The interval between the 28th & 19th harmonics, 28:19, measures approximately 671.3 ¢, which is 3.7 ¢ away from 16edo's "narrow fifth". Another voicing for this chord is 14:16:19, which features 19:14 as the outer interval (528.7 ¢ just, 525.0 ¢ in 16edo). A perhaps more consonant open voicing is 7:16:19
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 15.7540 | 15.8089 | 16dff | ⟨16 25 37 44 55 58] |
| 15.8089 | 15.8512 | 16d | ⟨16 25 37 44 55 59] |
| 15.8512 | 16.0431 | 16 | ⟨16 25 37 45 55 59] |
| 16.0431 | 16.0792 | 16e | ⟨16 25 37 45 56 59] |
| 16.0792 | 16.0887 | 16ef | ⟨16 25 37 45 56 60] |
| 16.0887 | 16.1504 | 16bef | ⟨16 26 37 45 56 60] |
| 16.1504 | 16.2074 | 16bcef | ⟨16 26 38 45 56 60] |
Commas
16et tempers out the following commas. (Note: This assumes val ⟨16 25 37 45 55 59].)
| Prime limit |
Ratio[note 1] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 5 | 135/128 | [-7 3 1⟩ | 92.18 | Layobi | Mavila comma, major chroma |
| 5 | 648/625 | [3 4 -4⟩ | 62.57 | Quadgu | Diminished comma, major diesis |
| 5 | 3125/3072 | [-10 -1 5⟩ | 29.61 | Laquinyo | Magic comma |
| 5 | (20 digits) | [23 6 -14⟩ | 3.34 | Sasepbiru | Vishnuzma |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Mint comma, septimal quartertone |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma |
| 7 | 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Jubilisma |
| 7 | 64827/64000 | [-9 3 -3 4⟩ | 22.23 | Laquadzo-atrigu | Squalentine comma |
| 7 | 3125/3087 | [0 -2 5 -3⟩ | 21.18 | Triru-aquinyo | Gariboh comma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.79 | Zotrigu | Starling comma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.43 | Latrizo | Gamelisma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutrigu | Porwell comma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
| 11 | 3025/3024 | [-4 -3 2 -1 2⟩ | 0.57 | Loloruyoyo | Lehmerisma |
Rank-2 temperaments
| Periods per 8ve |
Generator | Temperaments |
|---|---|---|
| 1 | 1\16 | Valentine, slurpee |
| 1 | 3\16 | Gorgo |
| 1 | 5\16 | Magic/muggles |
| 1 | 7\16 | Mavila/armodue |
| 2 | 1\16 | Bipelog |
| 2 | 3\16 | Lemba, astrology |
| 4 | 1\16 | Diminished/demolished |
| 8 | 1\16 | Semidim |
Octave stretch or compression
Having a flat tendency, 16et is best tuned with stretched octaves, which improve the accuracy of wide-voiced JI chords and rooted harmonics especially on inharmonic timbres such as bells and gamelan, with 57ed12 being a good option.
What follows is a comparison of stretched- and compressed-octave 16edo tunings.
- 16edo
- Step size: 75.000 ¢, octave size: 1200.0 ¢
Pure-octaves 16edo approximates all harmonics up to 16 within 36.7 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -27.0 | +0.0 | -11.3 | -27.0 | +6.2 | +0.0 | +21.1 | -11.3 | -26.3 | -27.0 |
| Relative (%) | +0.0 | -35.9 | +0.0 | -15.1 | -35.9 | +8.2 | +0.0 | +28.1 | -15.1 | -35.1 | -35.9 | |
| Steps (reduced) |
16 (0) |
25 (9) |
32 (0) |
37 (5) |
41 (9) |
45 (13) |
48 (0) |
51 (3) |
53 (5) |
55 (7) |
57 (9) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -15.5 | +6.2 | +36.7 | +0.0 | -30.0 | +21.1 | +2.5 | -11.3 | -20.8 | -26.3 | -28.3 | -27.0 |
| Relative (%) | -20.7 | +8.2 | +49.0 | +0.0 | -39.9 | +28.1 | +3.3 | -15.1 | -27.7 | -35.1 | -37.7 | -35.9 | |
| Steps (reduced) |
59 (11) |
61 (13) |
63 (15) |
64 (0) |
65 (1) |
67 (3) |
68 (4) |
69 (5) |
70 (6) |
71 (7) |
72 (8) |
73 (9) | |
- Step size: 75.105 ¢, octave size: 1201.7 ¢
Stretching the octave of 16edo by around 2 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 31.8 ¢. Its 2.5.7.13 WE tuning and 2.5.7.13 TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.7 | -24.3 | +3.4 | -7.4 | -22.7 | +10.9 | +5.0 | +26.4 | -5.7 | -20.5 | -21.0 |
| Relative (%) | +2.2 | -32.4 | +4.5 | -9.9 | -30.2 | +14.5 | +6.7 | +35.2 | -7.7 | -27.4 | -27.9 | |
| Step | 16 | 25 | 32 | 37 | 41 | 45 | 48 | 51 | 53 | 55 | 57 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -9.3 | +12.6 | -31.8 | +6.7 | -23.1 | +28.1 | +9.6 | -4.1 | -13.4 | -18.9 | -20.7 | -19.3 |
| Relative (%) | -12.4 | +16.7 | -42.3 | +8.9 | -30.8 | +37.4 | +12.8 | -5.4 | -17.9 | -25.1 | -27.6 | -25.7 | |
| Step | 59 | 61 | 62 | 64 | 65 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | |
- Step size: 75.262 ¢, octave size: 1204.2 ¢
Stretching the octave of 16edo by around 4 ¢ results in very improved primes 3, 5, 11 and 13, but much worse primes 2 and 7. This approximates all harmonics up to 16 within 34.5 ¢. The tunings 15zpi and 59ed13 both do this, their octaves differ from one another by less than 0.1 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +4.2 | -20.4 | +8.4 | -1.6 | -16.2 | +18.0 | +12.6 | +34.5 | +2.6 | -11.9 | -12.0 |
| Relative (%) | +5.6 | -27.1 | +11.1 | -2.2 | -21.5 | +23.9 | +16.7 | +45.8 | +3.4 | -15.8 | -16.0 | |
| Step | 16 | 25 | 32 | 37 | 41 | 45 | 48 | 51 | 53 | 55 | 57 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.1 | +22.2 | -22.0 | +16.8 | -12.9 | -36.6 | +20.3 | +6.8 | -2.4 | -7.7 | -9.4 | -7.8 |
| Relative (%) | -0.1 | +29.4 | -29.3 | +22.3 | -17.2 | -48.7 | +27.0 | +9.0 | -3.2 | -10.3 | -12.5 | -10.4 | |
| Step | 59 | 61 | 62 | 64 | 65 | 66 | 68 | 69 | 70 | 71 | 72 | 73 | |
- Step size: 75.315 ¢, octave size: 1205.0 ¢
Stretching the octave of 16edo by around 5 ¢ results in very improved primes 3, 5, 11 and 13, but much worse primes 2 and 7. This approximates all harmonics up to 16 within 37.2 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this. So does the tuning 37ed5, whose octave differs by only 0.1 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +5.0 | -19.1 | +10.1 | +0.3 | -14.0 | +20.3 | +15.1 | +37.2 | +5.4 | -9.0 | -9.0 |
| Relative (%) | +6.7 | -25.3 | +13.4 | +0.5 | -18.6 | +27.0 | +20.1 | +49.3 | +7.1 | -11.9 | -11.9 | |
| Step | 16 | 25 | 32 | 37 | 41 | 45 | 48 | 51 | 53 | 55 | 57 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.1 | +25.4 | -18.7 | +20.2 | -9.5 | -33.1 | +23.9 | +10.4 | +1.3 | -4.0 | -5.6 | -4.0 |
| Relative (%) | +4.1 | +33.7 | -24.9 | +26.8 | -12.6 | -44.0 | +31.7 | +13.8 | +1.7 | -5.2 | -7.4 | -5.3 | |
| Step | 59 | 61 | 62 | 64 | 65 | 66 | 68 | 69 | 70 | 71 | 72 | 73 | |
- Step size: 75.473 ¢, octave size: 1207.6 ¢
Stretching the octave of 16edo by around 7.5 ¢ results in especially improved primes 3, 5 and 11, but far worse primes 2 and 7. This approximates all harmonics up to 16 within 35.0 ¢. The tunings 57ed12 and 55ed11 both do this, their octaves differ from one another by only 0.1 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +7.6 | -15.1 | +15.1 | +6.2 | -7.6 | +27.5 | +22.7 | -30.3 | +13.7 | -0.3 | +0.0 |
| Relative (%) | +10.0 | -20.1 | +20.1 | +8.2 | -10.0 | +36.4 | +30.1 | -40.1 | +18.2 | -0.4 | +0.0 | |
| Steps (reduced) |
16 (16) |
25 (25) |
32 (32) |
37 (37) |
41 (41) |
45 (45) |
48 (48) |
50 (50) |
53 (53) |
55 (55) |
57 (0) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +12.4 | +35.0 | -8.9 | +30.3 | +0.8 | -22.7 | +34.6 | +21.3 | +12.3 | +7.3 | +5.8 | +7.6 |
| Relative (%) | +16.4 | +46.4 | -11.9 | +40.1 | +1.0 | -30.1 | +45.9 | +28.2 | +16.3 | +9.6 | +7.7 | +10.0 | |
| Steps (reduced) |
59 (2) |
61 (4) |
62 (5) |
64 (7) |
65 (8) |
66 (9) |
68 (11) |
69 (12) |
70 (13) |
71 (14) |
72 (15) |
73 (16) | |
Scales
Important mosses include:
- magic anti-diatonic 3L4s 1414141 (5\16, 1\1)
- magic superdiatonic 3L7s 1311311311 (5\16, 1\1)
- magic chromatic 11121121112 3L10s (5\16, 1\1)
- mavila anti-diatonic 2L5s 2223223 (9\16, 1\1)
- mavila superdiatonic 7L2s 222212221 (9\16, 1\1)
- gorgo 5L1s 333331 (3\16, 1\1)
- lemba 4L2s 332332 (3\16, 1\2)
Mavila
| [5]: | 5 2 5 2 2 | |
| [7]: | 3 2 2 3 2 2 2 | |
| [9]: | 1 2 2 2 1 2 2 2 2 |
See also Mavila Temperament Modal Harmony.
Diminished
| [8]: | 1 3 1 3 1 3 1 3 | |
| [12]: | 1 1 2 1 1 2 1 1 2 1 1 2 |
Magic
[7]: 1 4 1 4 1 4 1
[10]: 1 3 1 1 3 1 1 1 3 1
[13]: 1 1 2 1 1 1 2 1 1 1 2 1 1
Cynder/Gorgo
[5]: 3 3 4 3 3
[6]: 3 3 1 3 3 3
[11]: 1 2 1 2 1 2 1 2 1 2 1
Lemba/Astrology
[4]: 3 5 3 5
[6]: 3 2 3 3 2 3
[10]: 2 1 2 1 2 2 1 2 1 2
Metallic harmony
In 16edo, triadic harmony can be based on on heptatonic sevenths (or seconds) rather than thirds. For instance, 16edo approximates 7/4 well enough to use
it in place of the usual 3/2, and in Mavila[7] this 7/4 approximation shares an interval class with a well-approximated 11/6 (at 1050 ¢). Stacking these two intervals reaches 2025 ¢, or a minor 6th plus an octave. Thus the out-of-tune 675 ¢ interval is bypassed, and all the dyads in the triad are consonant.
Depending on whether the Mavila[7] major 7th or minor 7th is used, one of two triads is produced: a small one, 0 – 975 – 2025 ¢, and a large one, 0 – 1050 – 2025 ¢. William Lynch, a major proponent of this style of harmony, calls these two triads "hard" and "soft", respectively. In addition, two other "symmetrical" triads are also obvious possible chords: a narrow symmetrical triad at 0 – 975 – 1950 ¢, and a wide symmetrical triad at 0 – 1050 – 2100 ¢. These are sort of analogous to "diminished" and "augmented" triads. The characteristic buzzy/metallic sound of these seventh-based triads inspired William Lynch to call them "Metallic triads".
MOS scales supporting metallic harmony in 16edo
The ssLsssL mode of Mavila[7] contains two hard triads on degrees 1 and 4 and two soft triads on degrees 2 and 6. The other three chords are wide symmetrical triads 0-1050-2025 ¢. In Mavila[9], hard and soft triads cease to share a triad class, as 975 ¢ is a major 8th, while 1050 ¢ is a minor 9th; the triads may still be used, but parallel harmonic motion will function differently.
Another possible MOS scales for this approach would be Lemba[6], which gives two each of the soft, hard, and narrow symmetric triads.
See: Metallic Harmony.
Diagrams
16-tone piano layout based on the mavila[7]/antidiatonic scale
This Layout places mavila[7] on the black keys and mavila[9] on the white keys, according to antidiatonic notation.
Interleaved edos
A visualization of 16edo being two interleaved copies of 8edo and four interleaved copies of 4edo.
Lumatone mapping
See: Lumatone mapping for 16edo
Interval arithmetic examples
These examples show the correspondence between interval arithmetic using diatonic and antidiatonic notation.
| Diatonic (i.e. 12edo) | Antidiatonic (i.e. 16edo) | ||
|---|---|---|---|
| Question | Result | Question | Result |
| M2 + M2 | aug3 | m2 + m2 | dim3 |
| D to F♯ | aug3 | D to F♭ | dim3 |
| D to F | M3 | D to F | m3 |
| E♭ + m3 | Gbb | E♯ + M3 | G♯♯ |
| E♭ + P5 | B♭ | E♯ + P5 | B♯ |
| A minor chord | A C♭ E | A major chord | A C♯ E |
| E♭ major chord | E♭ G♭ D♭ | E♯ minor chord | E♯ G♯ B♯ |
| Gm7 = G + m3 + P5 + m7 | G B D F♭ | G + M3 + P5 + M7 | G B D F♯ |
| A♭7aug = A♭ + M3 + A5 + m7 | A♭ C♭ E Gbb | A♯ + m3 + d5 + M7 | A♯ C♯ E G♯♯ |
| what chord is D F A♯? | D + M3 + A5 = Daug | D F A♭ | D + m3 + d5 |
| what chord is C E G♭ B♭? | C + m3 + d5 + d7 = Cdim7 | C E G♯ B♯ | C + M3 + A5 + A7 |
| C major scale = C + M2 + M3 + P4 + P5 + M6 + M7 + P8 |
C D♯ E♯ F G A♯ B♯ C |
C + m2 + m3 + P4 + P5 + m6 + m7 + P8 |
C D♭ E♭ F G A♭ B♭ C |
| C minor scale = C + M2 + m3 + P4 + P5 + m6 + m7 + P8 |
C D♯ E F G A B C |
C + m2 + M3 + P4 + P5 + M6 + M7 + P8 |
C D♭ E F G A B C |
| what scale is A B♯ C♭ D E F G♭ A? |
A + M2 + m3 + P4 + P5 + M6 + m7 = A dorian |
A B♭ C♯ D E F G♯ A |
A + m2 + M3 + P4 + P5 + m6 + M7 |
Music
- See also: Category:16edo tracks
- it's not not opposite day (2023)
- nightfall (2024)
- 16edo jam (2025)
- Waltz in 16edo (2025)
- Enantiodromia (album) (from 2013)
- Maniacal Meditations (EP) (2013 EP)
- Mavila Fugue
- Canon at the Semitone on The Mother's Malison Theme, for Cor Anglais and Violin (for Organ)
- Canon on Twinkle Twinkle Little Star, for Organ (2023) (for Baroque Oboe and Viola)
- Baroque Micropiece in 16edo (2024)
- Edolian - Seventhic (2020)
- Finality (2021)
- Don't Take Five (2021)
- "Robotic Dialogue" from Microtones & Garden Gnomes (2017) Bandcamp | YouTube
- "Cognitive Climate" from Science Fraction (2022) Spotify | Bandcamp | YouTube
Notes
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
See also
- 57ed12 - octave stretched version of 16edo; 57ed12 improves 3.5.11.13.17 but damages 2.7
Approaches
References
Further reading
- Sword, Ron. Hexadecaphonic Scales for Guitar: A Microtonal Guitar Method Book, for Theory, Scales, and Information on the Sixteen Equal Division Octave System. 2009. (semi-diminished fourth tuning)
- Sword, Ron. Hexadecaphonic Scales for Guitar: Theory, Scales and Information on the Sixteen Equal Division Octave system. 2010? (superfourth tuning)
- Sword, Ron. "Thesaurus of Melodic Patterns and Intervals for 16-Tones" IAAA Press, USA. First Ed: August, 2011[citation needed]