Augmented family

From Xenharmonic Wiki
Revision as of 16:02, 21 August 2025 by FloraC (talk | contribs) (- CTE & POTE tunings)
Jump to navigation Jump to search
This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.

The 5-limit parent comma for the augmented family is 128/125, the diesis. The period is 1/3 octave, and this is what is used for 5/4, the classical major third. The generator can be taken as a fifth or a semitone, and 12edo, with its excellent fifth, is an obvious tuning for 5-limit augmented, though a sharper fifth might be preferred to go with the sharp third.

Augmented

Subgroup: 2.3.5

Comma list: 128/125

Mapping: [⟨3 0 7], ⟨0 1 0]]

mapping generators: ~5/4, ~3

Optimal tunings:

  • WE: ~5/4 = 399.0128 ¢, ~3/2 = 704.8937 ¢ (~16/15 = 93.1320 ¢)
error map: ⟨-2.962 -0.023 +6.776]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 705.0691 ¢ (~16/15 = 94.9309 ¢)
error map: ⟨0.000 +3.114 +13.686]

Optimal ET sequence: 3, 9, 12, 27, 39, 51c, 90cc

Badness (Sintel): 0.523

Overview to extensions

The second comma of the normal comma list defines which 7-limit family member we are looking at. August adds 36/35, augene 64/63, hexe 256/245, hemiaug 245/243, and triforce 49/48. Hexe splits the period to 1/6 octave, and hemiaug the generator, giving quartertones instead of semitones.

August

Subgroup: 2.3.5.7

Comma list: 36/35, 128/125

Mapping: [⟨3 0 7 -1], ⟨0 1 0 2]]

Optimal tunings:

  • WE: ~5/4 = 399.1036 ¢, ~3/2 = 694.4509 ¢ (~16/15 = 103.7564 ¢)
error map: ⟨-2.689 -10.193 +7.412 +15.594]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 694.6812 ¢ (~16/15 = 105.3188 ¢)
error map: ⟨0.000 -7.274 +13.686 +20.537]

Optimal ET sequence: 9, 12, 45cd

Badness (Sintel): 0.670

11-limit

Subgroup: 2.3.5.7.11

Comma list: 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1], ⟨0 1 0 2 2]]

Optimal tunings:

  • WE: ~5/4 = 398.9225 ¢, ~3/2 = 690.6486 ¢ (~16/15 = 107.1966 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 690.8519 ¢ (~16/15 = 109.1481 ¢)

Optimal ET sequence: 9, 12, 21, 33e

Badness (Sintel): 0.668

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 27/26, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 -3], ⟨0 1 0 2 2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.0956 ¢, ~3/2 = 687.2261 ¢ (~16/15 = 110.9651 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 687.5057 ¢ (~16/15 = 112.4943 ¢)

Optimal ET sequence: 9, 12f, 21, 33ef

Badness (Sintel): 0.762

Augustus

Subgroup: 2.3.5.7.11.13

Comma list: 26/25, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 11], ⟨0 1 0 2 2 0]]

Optimal tunings:

  • WE: ~5/4 = 400.4230 ¢, ~3/2 = 686.0809 ¢ (~16/15 = 114.7650 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 685.8446 ¢ (~16/15 = 114.1554 ¢)

Optimal ET sequence: 9, 12

Badness (Sintel): 0.919

Augene

Main article: Augene

Subgroup: 2.3.5.7

Comma list: 64/63, 126/125

Mapping: [⟨3 0 7 18], ⟨0 1 0 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.7461 ¢, ~3/2 = 707.0335 ¢ (~21/20 = 90.4587 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 709.3249 ¢ (~21/20 = 90.6751 ¢)
error map: ⟨0.000 +7.370 +13.686 +12.524]

Optimal ET sequence: 12, 27, 39d, 66cd

Badness (Sintel): 0.628

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 64/63, 100/99

Mapping: [⟨3 0 7 18 20], ⟨0 1 0 -2 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.4962 ¢, ~3/2 = 708.5030 ¢ (~21/20 = 88.4895 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 711.6031 ¢ (~21/20 = 88.3969 ¢)

Optimal ET sequence: 12, 15, 27e

Badness (Sintel): 0.648

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 40/39, 56/55, 64/63, 66/65

Mapping: [⟨3 0 7 18 20 16], ⟨0 1 0 -2 -2 -1]]

Optimal tunings:

  • WE: ~5/4 = 398.0488 ¢, ~3/2 = 708.5402 ¢ (~21/20 = 87.5574 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.6704 ¢ (~21/20 = 87.3296 ¢)

Optimal ET sequence: 12f, 15, 27eff

Badness (Sintel): 0.859

Ogene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 91/90, 100/99

Mapping: [⟨3 0 7 18 20 -8], ⟨0 1 0 -2 -2 4]]

Optimal tunings:

  • WE: ~5/4 = 398.6473 ¢, ~3/2 = 710.1987 ¢ (~21/20 = 87.0959 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.5057 ¢ (~21/20 = 87.4943 ¢)

Optimal ET sequence: 12, 15, 27e, 69bceef

Badness (Sintel): 0.946

Agene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 78/77, 100/99

Mapping: [⟨3 0 7 18 20 35], ⟨0 1 0 -2 -2 -5]]

Optimal tunings:

  • WE: ~5/4 = 398.5229 ¢, ~3/2 = 707.0562 ¢ (~21/20 = 89.9897 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 710.1903 ¢ (~21/20 = 89.8097 ¢)

Optimal ET sequence: 12f, 27e, 66cdeeef

Badness (Sintel): 0.955

Eugene

Subgroup: 2.3.5.7.11

Comma list: 55/54, 64/63, 77/75

Mapping: [⟨3 0 7 18 -4], ⟨0 1 0 -2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.1743 ¢, ~3/2 = 712.6763 ¢ (~21/20 = 85.6723 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 713.9414 ¢ (~21/20 = 86.0586 ¢)

Optimal ET sequence: 12e, 15, 27, 42

Badness (Sintel): 1.18

Inflated

Subgroup: 2.3.5.7

Comma list: 28/27, 128/125

Mapping: [⟨3 0 7 -6], ⟨0 1 0 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4023 ¢, ~3/2 = 719.8327 ¢ (~25/24 = 76.9719 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 721.0196 ¢ (~25/24 = 78.9804 ¢)
error map: ⟨0.000 +19.065 +13.686 -5.767]

Optimal ET sequence: 3d, 12d, 15

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 28/27, 55/54, 128/125

Mapping: [⟨3 0 7 -6 -4], ⟨0 1 0 3 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4016 ¢, ~3/2 = 719.7758 ¢ (~25/24 = 77.0275 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 720.9386 ¢ (~25/24 = 79.0614 ¢)

Optimal ET sequence: 3de, 12de, 15

Badness (Sintel): 1.03

Deflated

Subgroup: 2.3.5.7

Comma list: 21/20, 128/125

Mapping: [⟨3 0 7 13], ⟨0 1 0 -1]]

Optimal tunings:

  • WE: ~5/4 = 401.9566 ¢, ~3/2 = 684.9634 ¢ (~16/15 = 118.9497 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 682.2587 ¢ (~16/15 = 117.7413 ¢)
error map: ⟨0.000 -19.696 +13.686 -51.085]

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.50

11-limit

Subgroup: 2.3.5.7.11

Comma list: 21/20, 33/32, 128/125

Mapping: [⟨3 0 7 13 15], ⟨0 1 0 -1 -1]]

Optimal tunings:

  • WE: ~5/4 = 402.1799 ¢, ~3/2 = 683.7477 ¢ (~16/15 = 120.6120 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 680.0162 ¢ (~16/15 = 119.9838 ¢)

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.23

Hexe

Subgroup: 2.3.5.7

Comma list: 50/49, 128/125

Mapping: [⟨6 0 14 17], ⟨0 1 0 0]]

mapping generators: ~28/25, ~3

Optimal tunings:

  • WE: ~28/25 = 199.0488 ¢, ~3/2 = 707.5815 ¢ (~25/24 = 88.6137 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 708.6907 ¢ (~25/24 = 91.3093 ¢)
error map: ⟨0.000 +6.735 +13.686 +31.174]

Optimal ET sequence: 6, 12, 30d, 42dd, 54cdd

Badness (Sintel): 1.46

11-limit

Subgroup: 2.3.5.7.11

Comma list: 50/49, 56/55, 125/121

Mapping: [⟨6 0 14 17 21], ⟨0 1 0 0 0]]

Optimal tunings:

  • WE: ~28/25 = 198.6942 ¢, ~3/2 = 709.6404 ¢ (~25/24 = 85.1362 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 711.8043 ¢ (~25/24 = 88.1957 ¢)

Optimal ET sequence: 6, 12, 30dee, 42ddeee

Badness (Sintel): 1.27

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 50/49, 56/55, 66/65, 105/104

Mapping: [⟨6 0 14 17 21 13], ⟨0 1 0 0 0 1]]

Optimal tunings:

  • WE: ~28/25 = 198.4492 ¢, ~3/2 = 704.4994 ¢ (~25/24 = 89.2973 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 706.6050 ¢ (~16/15 = 93.3950 ¢)

Optimal ET sequence: 6f, 12f

Badness (Sintel): 1.49

Triforce

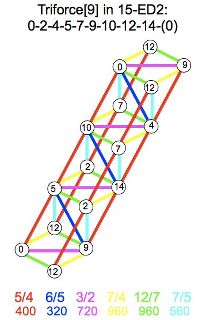
triforce9.jpg
Lattice of triforce

Subgroup: 2.3.5.7

Comma list: 49/48, 128/125

Mapping: [⟨3 0 7 6], ⟨0 2 0 1]]

mapping generators: ~5/4, ~7/4

Optimal tunings:

  • WE: ~5/4 = 399.7480 ¢, ~7/4 = 952.3507 ¢ (~35/32 = 152.8547 ¢)
error map: ⟨-0.756 +2.746 +11.922 -17.987]
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7463 ¢ (~35/32 = 152.7463 ¢)
error map: ⟨0.000 +3.538 +13.686 -16.080]

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 49/48, 56/55, 77/75

Mapping: [⟨3 0 7 6 8], ⟨0 2 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 399.7654 ¢, ~7/4 = 952.3730 ¢ (~12/11 = 152.8421 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7447 ¢ (~12/11 = 152.7447 ¢)

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 0.865

Music

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 66/65, 77/75

Mapping: [⟨3 0 7 6 8 4], ⟨0 2 0 1 1 3]]

Optimal tunings:

  • WE: ~5/4 = 399.7107 ¢, ~7/4 = 950.9983 ¢ (~12/11 = 151.5768 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 951.4465 ¢ (~12/11 = 151.4465 ¢)

Optimal ET sequence: 6f, 9, 15, 24

Badness (Sintel): 0.837

Scales
  • triphi, Triforce[9] with L:s = phi

Semitriforce

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 77/75, 507/500

Mapping: [⟨6 0 14 12 16 27], ⟨0 2 0 1 1 -1]]

mapping generators: ~44/39, ~7/4

Optimal tunings:

  • WE: ~44/39 = 199.8321 ¢, ~7/4 = 952.5580 ¢ (~40/39 = 46.6024 ¢)
  • CWE: ~44/39 = 200.0000 ¢, ~7/4 = 953.2005 ¢ (~40/39 = 46.7995 ¢)

Optimal ET sequence: 6, 18bd, 24

Badness (Sintel): 2.44

Hemiaug

Subgroup: 2.3.5.7

Comma list: 128/125, 245/243

Mapping: [⟨3 1 7 -1], ⟨0 2 0 5]]

mapping generators: ~5/4, ~14/9

Optimal tunings:

  • WE: ~5/4 = 398.9278 ¢, ~14/9 = 752.8583 ¢ (~36/35 = 44.9973 ¢)
error map: ⟨-3.217 +2.689 +6.181 -3.462]
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 754.2078 ¢ (~36/35 = 45.7922 ¢)
error map: ⟨0.000 +6.461 +13.686 +2.213]

Optimal ET sequence: 24, 27

Badness (Sintel): 1.78

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 243/242

Mapping: [⟨3 1 7 -1 1], ⟨0 2 0 5 5]]

Optimal tunings:

  • WE: ~5/4 = 398.8946 ¢, ~14/9 = 752.1272 ¢ (~36/35 = 45.6619 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.5000 ¢ (~36/35 = 46.5000 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.26

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 91/90, 128/125, 245/243

Mapping: [⟨3 1 7 -1 1 13], ⟨0 2 0 5 5 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.1053 ¢, ~14/9 = 752.0643 ¢ (~36/35 = 46.1463 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.3806 ¢ (~36/35 = 46.6194 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.25

Hemiug

Subgroup: 2.3.5.7

Comma list: 128/125, 1323/1250

Mapping: [⟨3 1 7 14], ⟨0 2 0 -3]]

mapping generators: ~5/4, ~32/21

Optimal tunings:

  • WE: ~5/4 = 400.1805 ¢, ~32/21 = 748.2436 ¢ (~21/20 = 52.1174 ¢)
error map: ⟨+0.542 -5.287 +14.950 -11.030]
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 747.9138 ¢ (~21/20 = 52.0862 ¢)
error map: ⟨0.000 -6.127 +13.686 -12.567]

Optimal ET sequence: 21, 24, 45c

Badness (Sintel): 3.49

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 1323/1250

Mapping: [⟨3 1 7 14 16], ⟨0 2 0 -3 -3]]

Optimal tunings:

  • WE: ~5/4 = 400.0637 ¢, ~32/21 = 748.4638 ¢ (~33/32 = 51.6637 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.3383 ¢ (~33/32 = 51.6617 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 2.25

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 66/65, 105/104, 507/500

Mapping: [⟨3 1 7 14 16 13], ⟨0 2 0 -3 -3 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.8855 ¢, ~32/21 = 748.2378 ¢ (~33/32 = 51.5332 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.4655 ¢ (~33/32 = 51.5345 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 1.75

Oodako

Subgroup: 2.3.5.7

Comma list: 128/125, 2401/2400

Mapping: [⟨3 3 7 8], ⟨0 4 0 1]]

mapping generators: ~5/4, ~28/25

Optimal tunings:

  • WE: ~5/4 = 399.0296 ¢, ~28/25 = 176.2174 ¢ (~49/48 = 46.5949 ¢)
error map: ⟨-2.911 +0.004 +6.894 -0.371]
  • CWE: ~5/4 = 400.0000 ¢, ~28/25 = 176.2984 ¢ (~49/48 = 47.4031 ¢)
error map: ⟨0.000 +3.239 +13.686 +7.473]

Optimal ET sequence: 6, 21, 27, 75c, 102ccd, 129bccd

Badness (Sintel): 2.86

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 2401/2400

Mapping: [⟨3 3 7 8 10], ⟨0 4 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 398.6615 ¢, ~11/10 = 176.3886 ¢ (~49/48 = 45.8843 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.5471 ¢ (~49/48 = 46.9059 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.96

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 128/125, 507/500

Mapping: [⟨3 3 7 8 10 12], ⟨0 4 0 1 1 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.8612 ¢, ~11/10 = 176.0486 ¢ (~49/48 = 46.7640 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.3326 ¢ (~49/48 = 47.3348 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.75

Hemisemiaug

Subgroup: 2.3.5.7

Comma list: 128/125, 12005/11664

Mapping: [⟨6 1 14 4], ⟨0 2 0 3]]

mapping generators: ~54/49, ~45/28

Optimal tunings:

  • WE: ~54/49 = 199.5469 ¢, ~45/28 = 853.5468 ¢ (~36/35 = 55.3594 ¢)
error map: ⟨-2.719 +4.686 +7.342 -9.998]
  • CWE: ~54/49 = 200.0000 ¢, ~45/28 = 854.7144 ¢ (~36/35 = 54.7144 ¢)
error map: ⟨0.000 +7.474 +13.686 -4.683]

Optimal ET sequence: 18, 24, 42

Badness (Sintel): 5.34

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 3773/3645

Mapping: [⟨6 1 14 4 8], ⟨0 2 0 3 3]]

Optimal tunings:

  • WE: ~54/49 = 199.5188 ¢, ~18/11 = 853.1623 ¢ (~36/35 = 55.0872 ¢)
  • CWE: ~54/49 = 200.0000 ¢, ~18/11 = 854.3545 ¢ (~36/35 = 54.3545 ¢)

Optimal ET sequence: 18e, 24, 42e, 66ce, 108bccee

Badness (Sintel): 2.67

Niner

Niner gives 9 as the complexity of an otonal tetrad, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads.

Subgroup: 2.3.5.7

Comma list: 128/125, 686/675

Mapping: [⟨9 0 21 11], ⟨0 1 0 1]]

mapping generators: ~49/45, ~3

Optimal tunings:

  • WE: ~49/45 = 133.0272 ¢, ~3/2 = 705.5438 ¢ (~36/35 = 40.4075 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~49/45 = 133.3333 ¢, ~3/2 = 705.5157 ¢ (~36/35 = 38.8490 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 9, 18, 27, 63c, 90cc

Badness (Sintel): 1.70

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 540/539

Mapping: [⟨9 0 21 11 17], ⟨0 1 0 1 1]]

Optimal tunings:

  • WE: ~12/11 = 132.9553 ¢, ~3/2 = 704.7217 ¢ (~36/35 = 39.9453 ¢)
  • CWE: ~12/11 = 133.3333 ¢, ~3/2 = 704.5723 ¢ (~36/35 = 37.9056 ¢)

Optimal ET sequence: 9, 18e, 27e, 63cee

Badness (Sintel): 1.15

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 91/90, 128/125

Mapping: [⟨9 0 21 11 17 19], ⟨0 1 0 1 1 1]]

Optimal tunings:

  • WE: ~14/13 = 133.0143 ¢, ~3/2 = 705.1969 ¢ (~36/35 = 40.1256 ¢)
  • CWE: ~14/13 = 133.3333 ¢, ~3/2 = 705.0176 ¢ (~36/35 = 38.3510 ¢)

Optimal ET sequence: 9, 18e, 27e

Badness (Sintel): 0.998

Trug

Subgroup: 2.3.5.7

Comma list: 128/125, 360/343

Mapping: [⟨3 1 7 6], ⟨0 3 0 2]]

mapping generators: ~5/4, ~48/35

Optimal tunings:

  • WE: ~5/4 = 398.2337 ¢, ~48/35 = 499.7635 ¢ (~15/14 = 101.5299 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~5/4 = 400.0000 ¢, ~48/35 = 500.9654 ¢ (~15/14 = 100.9654 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 3b, 9bd, 12

Badness (Sintel): 3.50

External links

Retrieved from "https://en.xen.wiki/index.php?title=Augmented_family&oldid=207913"