Augmented family: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
m Text replacement - "{{Technical data page}}<br><br>" to "{{Technical data page}}"
Tags: Mobile edit Mobile web edit
Intro to some of these temps
 
(8 intermediate revisions by 3 users not shown)
Line 4: Line 4:
}}
}}
{{Technical data page}}
{{Technical data page}}
The 5-limit parent comma for the '''augmented family''' is [[128/125]], the diesis. The [[period]] is 1/3 octave, and this is what is used for 5/4, the classical major third. The [[generator]] can be taken as a fifth or a semitone, and [[12edo]], with its excellent fifth, is an obvious tuning for [[5-limit]] augmented, though a sharper fifth might be preferred to go with the sharp third.
The '''augmented family''' of [[regular temperament|temperaments]] [[tempering out|tempers out]] the diesis a.k.a. augmented comma, [[128/125]], the amount by which three [[5/4]] major thirds fall short of an [[2/1|octave]], and so identifies the major third with the 1/3-octave. Hence it has the same 400-cent 5/4-approximations as [[12edo]].  


== Augmented ==
== Augmented ==
The [[period]] is 1/3 octave, and this is what is used for 5/4, the classical major third. The [[generator]] can be taken as a fifth or a semitone, and [[12edo]], with its excellent fifth, is an obvious tuning for [[5-limit]] augmented, though a sharper fifth might be preferred to go with the sharp third. Its [[ploidacot]] is triploid monocot.
[[Subgroup]]: 2.3.5
[[Subgroup]]: 2.3.5


Line 16: Line 18:


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~3/2 = 701.955 (~16/15 = 98.045)
* [[WE]]: ~5/4 = 399.0128{{c}}, ~3/2 = 704.8937{{c}} (~16/15 = 93.1320{{c}})
: [[error map]]: {{val| 0.000 0.000 +13.686 }}
: [[error map]]: {{val| -2.962 -0.023 +6.776 }}
* [[POTE]]: ~5/4 = 400.000, ~3/2 = 706.638 (~16/15 = 93.362)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 705.0691{{c}} (~16/15 = 94.9309{{c}})
: error map: {{val| 0.000 +4.683 +13.686 }}
: error map: {{val| 0.000 +3.114 +13.686 }}


{{Optimal ET sequence|legend=1| 3, 12, 27, 39, 51c, 90cc }}
{{Optimal ET sequence|legend=1| 3, 9, 12, 27, 39, 51c, 90cc }}


[[Badness]] (Smith): 0.022315
[[Badness]] (Sintel): 0.523


=== Overview to extensions ===
=== Overview to extensions ===
The second comma of the [[Normal lists #Normal interval list|normal comma list]] defines which [[7-limit]] family member we are looking at. August adds [[36/35]], augene [[64/63]], hexe [[256/245]], hemiaug [[245/243]], and triforce [[49/48]]. Hexe splits the [[period]] to 1/6 octave, and hemiaug the [[generator]], giving quartertones instead of semitones.
The second comma of the [[Normal lists #Normal interval list|normal comma list]] defines which [[7-limit]] family member we are looking at. Augene adds [[64/63]], august [[36/35]], hexe [[256/245]], hemiaug [[245/243]], and triforce [[49/48]]. Hexe splits the [[period]] to 1/6 octave, and hemiaug the [[generator]], giving quartertones instead of semitones.
 
== Augene ==
{{Main| Augene }}
 
Augene tempers out 64/63 and 126/125. It may be described as the {{nowrap| 12 & 15 }} temperament. [[27edo]] and [[39edo]] in the 39d val make for good tunings.  


== August ==
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


[[Comma list]]: 36/35, 128/125
[[Comma list]]: 64/63, 126/125


{{Mapping|legend=1| 3 0 7 -1 | 0 1 0 2 }}
{{Mapping|legend=1| 3 0 7 18 | 0 1 0 -2 }}


{{Multival|legend=1| 3 0 6 -7 1 14 }}
[[Optimal tuning]]s:
* [[WE]]: ~5/4 = 398.7461{{c}}, ~3/2 = 707.0335{{c}} (~21/20 = 90.4587{{c}})
: [[error map]]: {{val| -3.762 +1.317 +4.909 +2.060 }}
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 709.3249{{c}} (~21/20 = 90.6751{{c}})
: error map: {{val| 0.000 +7.370 +13.686 +12.524 }}


[[Optimal tuning]]s:
{{Optimal ET sequence|legend=1| 12, 27, 39d, 66cd }}
* [[CTE]]: ~5/4 = 400.000, ~3/2 = 692.124 (~16/15 = 107.876)
: [[error map]]: {{val| 0.000 -9.831 +13.686 +15.422 }}
* [[POTE]]: ~5/4 = 400.000, ~3/2 = 696.011 (~16/15 = 103.989)
: error map: {{val| 0.000 -5.944 +13.686 +23.195 }}
 
{{Optimal ET sequence|legend=1| 9, 12, 45cd }}


[[Badness]] (Smith): 0.026459
[[Badness]] (Sintel): 0.628


=== 11-limit ===
=== 11-limit ===
Subgroup: 2.3.5.7.11
Subgroup: 2.3.5.7.11


Comma list: 36/35, 45/44, 56/55
Comma list: 56/55, 64/63, 100/99


Mapping: {{mapping| 3 0 7 -1 1 | 0 1 0 2 2 }}
Mapping: {{mapping| 3 0 7 18 20 | 0 1 0 -2 -2 }}


Wedgie: {{multival| 3 0 6 6 -7 1 -1 14 14 -4 }}
Optimal tunings:  
* WE: ~5/4 = 398.4962{{c}}, ~3/2 = 708.5030{{c}} (~21/20 = 88.4895{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 711.6031{{c}} (~21/20 = 88.3969{{c}})


Optimal tunings:
{{Optimal ET sequence|legend=0| 12, 15, 27e }}
* CTE: ~5/4 = 400.000, ~3/2 = 687.685 (~16/15 = 112.315)
* POTE: ~5/4 = 400.000, ~3/2 = 692.514 (~16/15 = 107.486)
 
{{Optimal ET sequence|legend=0| 9, 12, 21, 33e, 45cde }}


Badness (Smith): 0.020191
Badness (Sintel): 0.648


==== 13-limit ====
==== 13-limit ====
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11.13


Comma list: 27/26, 36/35, 45/44, 56/55
Comma list: 40/39, 56/55, 64/63, 66/65


Mapping: {{mapping| 3 0 7 -1 1 -3 | 0 1 0 2 2 3 }}
Mapping: {{mapping| 3 0 7 18 20 16 | 0 1 0 -2 -2 -1 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 685.084 (~16/15 = 114.916)
* WE: ~5/4 = 398.0488{{c}}, ~3/2 = 708.5402{{c}} (~21/20 = 87.5574{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 688.783 (~16/15 = 111.217)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 712.6704{{c}} (~21/20 = 87.3296{{c}})


{{Optimal ET sequence|legend=0| 9, 12f, 21, 33ef, 54bceeff }}
{{Optimal ET sequence|legend=0| 12f, 15, 27eff }}


Badness (Smith): 0.018448
Badness (Sintel): 0.859


==== Augustus ====
==== Ogene ====
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11.13


Comma list: 26/25, 36/35, 45/44, 56/55
Comma list: 56/55, 64/63, 91/90, 100/99


Mapping: {{mapping| 3 0 7 -1 1 11 | 0 1 0 2 2 0 }}
Mapping: {{mapping| 3 0 7 18 20 -8 | 0 1 0 -2 -2 4 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 687.685 (~16/15 = 112.315)
* WE: ~5/4 = 398.6473{{c}}, ~3/2 = 710.1987{{c}} (~21/20 = 87.0959{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 685.356 (~16/15 = 114.644)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 712.5057{{c}} (~21/20 = 87.4943{{c}})


{{Optimal ET sequence|legend=0| 9, 12, 21f }}
{{Optimal ET sequence|legend=0| 12, 15, 27e, 69bceef }}


Badness (Smith): 0.022236
Badness (Sintel): 0.946


== Augene ==
==== Agene ====
{{Main| Augene }}
Subgroup: 2.3.5.7.11.13


[[Subgroup]]: 2.3.5.7
Comma list: 56/55, 64/63, 78/77, 100/99


[[Comma list]]: 64/63, 126/125
Mapping: {{mapping| 3 0 7 18 20 35 | 0 1 0 -2 -2 -5 }}


{{Mapping|legend=1| 3 0 7 18 | 0 1 0 -2 }}
Optimal tunings:
* WE: ~5/4 = 398.5229{{c}}, ~3/2 = 707.0562{{c}} (~21/20 = 89.9897{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 710.1903{{c}} (~21/20 = 89.8097{{c}})


{{Multival|legend=1| 3 0 -6 -7 -18 -14 }}
{{Optimal ET sequence|legend=0| 12f, 27e, 66cdeeef }}


[[Optimal tuning]]s:
Badness (Sintel): 0.955
* [[CTE]]: ~5/4 = 400.000, ~3/2 = 709.595 (~21/20 = 90.405)
: [[error map]]: {{val| 0.000 +7.640 +13.686 +11.984 }}
* [[POTE]]: ~5/4 = 400.000, ~3/2 = 709.257 (~21/20 = 90.743)
: error map: {{val| 0.000 +7.302 +13.686 +12.660 }}


{{Optimal ET sequence|legend=1| 12, 27, 39d, 66cd }}
=== Eugene ===
 
[[Badness]] (Smith): 0.024816
 
=== 11-limit ===
Subgroup: 2.3.5.7.11
Subgroup: 2.3.5.7.11


Comma list: 56/55, 64/63, 100/99
Comma list: 55/54, 64/63, 77/75


Mapping: {{mapping| 3 0 7 18 20 | 0 1 0 -2 -2 }}
Mapping: {{mapping| 3 0 7 18 -4 | 0 1 0 -2 3 }}


Wedgie: {{multival| 3 0 -6 -6 -7 -18 -20 -14 -14 4 }}
Optimal tunings:  
* WE: ~5/4 = 399.1743{{c}}, ~3/2 = 712.6763{{c}} (~21/20 = 85.6723{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 713.9414{{c}} (~21/20 = 86.0586{{c}})


Optimal tunings:
{{Optimal ET sequence|legend=0| 12e, 15, 27, 42 }}
* CTE: ~5/4 = 400.000, ~3/2 = 713.570 (~21/20 = 86.430)
* POTE: ~5/4 = 400.000, ~3/2 = 711.177 (~21/20 = 88.823)


{{Optimal ET sequence|legend=0| 12, 15, 27e }}
Badness (Sintel): 1.18


Badness (Smith): 0.019613
== August ==
August tempers out 36/35 and 225/224. It may be described as the {{nowrap| 9 & 12 }} temperament. Unlike augene, august calls for a flat tuning of the fifth, and besides [[12edo]], [[21edo]] is among the possible tunings.  


==== 13-limit ====
[[Subgroup]]: 2.3.5.7
Subgroup: 2.3.5.7.11.13


Comma list: 40/39, 56/55, 64/63, 66/65
[[Comma list]]: 36/35, 128/125


Mapping: {{mapping| 3 0 7 18 20 16 | 0 1 0 -2 -2 -1 }}
{{Mapping|legend=1| 3 0 7 -1 | 0 1 0 2 }}


Optimal tunings:  
[[Optimal tuning]]s:  
* CTE: ~5/4 = 400.000, ~3/2 = 716.123 (~21/20 = 83.877)
* [[WE]]: ~5/4 = 399.1036{{c}}, ~3/2 = 694.4509{{c}} (~16/15 = 103.7564{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 712.013 (~21/20 = 87.987)
: [[error map]]: {{val| -2.689 -10.193 +7.412 +15.594 }}
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 694.6812{{c}} (~16/15 = 105.3188{{c}})
: error map: {{val| 0.000 -7.274 +13.686 +20.537 }}


{{Optimal ET sequence|legend=0| 12f, 15, 27eff }}
{{Optimal ET sequence|legend=1| 9, 12, 45cd }}


Badness (Smith): 0.020785
[[Badness]] (Sintel): 0.670


==== Ogene ====
=== 11-limit ===
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11


Comma list: 56/55, 64/63, 91/90, 100/99
Comma list: 36/35, 45/44, 56/55


Mapping: {{mapping| 3 0 7 18 20 -8 | 0 1 0 -2 -2 4 }}
Mapping: {{mapping| 3 0 7 -1 1 | 0 1 0 2 2 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 711.902 (~21/20 = 88.098)
* WE: ~5/4 = 398.9225{{c}}, ~3/2 = 690.6486{{c}} (~16/15 = 107.1966{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 712.609 (~21/20 = 87.391)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 690.8519{{c}} (~16/15 = 109.1481{{c}})


{{Optimal ET sequence|legend=0| 12, 15, 27e, 69bceef }}
{{Optimal ET sequence|legend=0| 9, 12, 21, 33e }}


Badness (Smith): 0.022890
Badness (Sintel): 0.668


==== Agene ====
==== 13-limit ====
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11.13


Comma list: 56/55, 64/63, 78/77, 100/99
Comma list: 27/26, 36/35, 45/44, 56/55


Mapping: {{mapping| 3 0 7 18 20 35 | 0 1 0 -2 -2 -5 }}
Mapping: {{mapping| 3 0 7 -1 1 -3 | 0 1 0 2 2 3 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 712.572 (~21/20 = 87.428)
* WE: ~5/4 = 399.0956{{c}}, ~3/2 = 687.2261{{c}} (~16/15 = 110.9651{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 709.677 (~21/20 = 90.323)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 687.5057{{c}} (~16/15 = 112.4943{{c}})


{{Optimal ET sequence|legend=0| 12f, 27e }}
{{Optimal ET sequence|legend=0| 9, 12f, 21, 33ef }}


Badness (Smith): 0.023113
Badness (Sintel): 0.762


=== Eugene ===
==== Augustus ====
Subgroup: 2.3.5.7.11
Subgroup: 2.3.5.7.11.13


Comma list: 55/54, 64/63, 77/75
Comma list: 26/25, 36/35, 45/44, 56/55


Mapping: {{mapping| 3 0 7 18 -4 | 0 1 0 -2 3 }}
Mapping: {{mapping| 3 0 7 -1 1 11 | 0 1 0 2 2 0 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 713.002 (~21/20 = 86.998)
* WE: ~5/4 = 400.4230{{c}}, ~3/2 = 686.0809{{c}} (~16/15 = 114.7650{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 714.150 (~21/20 = 85.850)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 685.8446{{c}} (~16/15 = 114.1554{{c}})


{{Optimal ET sequence|legend=0| 12e, 15, 27, 42 }}
{{Optimal ET sequence|legend=0| 9, 12 }}


Badness (Smith): 0.035554
Badness (Sintel): 0.919


== Inflated ==
== Inflated ==
Line 198: Line 196:


{{Mapping|legend=1| 3 0 7 -6 | 0 1 0 3 }}
{{Mapping|legend=1| 3 0 7 -6 | 0 1 0 3 }}
{{Multival|legend=1| 3 0 9 -7 6 21 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~3/2 = 717.517 (~25/24 = 82.483)
* [[WE]]: ~5/4 = 398.4023{{c}}, ~3/2 = 719.8327{{c}} (~25/24 = 76.9719{{c}})
: [[error map]]: {{val| 0.000 +15.562 +13.686 -16.274 }}
: [[error map]]: {{val| -3.762 +1.317 +4.909 +2.060 }}
* [[POTE]]: ~5/4 = 400.000, ~3/2 = 722.719 (~25/24 = 77.281)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 721.0196{{c}} (~25/24 = 78.9804{{c}})
: error map: {{val| 0.000 +20.764 +13.686 -0.668 }}
: error map: {{val| 0.000 +19.065 +13.686 -5.767 }}


{{Optimal ET sequence|legend=1| 3d, 12d, 15 }}
{{Optimal ET sequence|legend=1| 3d, 12d, 15 }}


[[Badness]] (Smith): 0.054729
[[Badness]] (Sintel): 1.39


=== 11-limit ===
=== 11-limit ===
Line 219: Line 215:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 717.382 (~25/24 = 82.618)
* WE: ~5/4 = 398.4016{{c}}, ~3/2 = 719.7758{{c}} (~25/24 = 77.0275{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 722.663 (~25/24 = 77.337)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 720.9386{{c}} (~25/24 = 79.0614{{c}})


{{Optimal ET sequence|legend=0| 3de, 12de, 15 }}
{{Optimal ET sequence|legend=0| 3de, 12de, 15 }}


Badness (Smith): 0.031171
Badness (Sintel): 1.03


== Deflated ==
== Deflated ==
Line 232: Line 228:


{{Mapping|legend=1| 3 0 7 13 | 0 1 0 -1 }}
{{Mapping|legend=1| 3 0 7 13 | 0 1 0 -1 }}
{{Multival|legend=1| 3 0 -3 -7 -13 -7 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~3/2 = 684.847 (~16/15 = 115.153)
* [[WE]]: ~5/4 = 401.9566{{c}}, ~3/2 = 684.9634{{c}} (~16/15 = 118.9497{{c}})
: [[error map]]: {{val| 0.000 -17.108 +13.686 -53.673 }}
: [[error map]]: {{val| +5.870 -11.122 +27.382 -34.224 }}
* [[POTE]]: ~5/4 = 400.000, ~3/2 = 681.629 (~16/15 = 118.371)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 682.2587{{c}} (~16/15 = 117.7413{{c}})
: error map: {{val| 0.000 -20.326 +13.686 -50.455 }}
: error map: {{val| 0.000 -19.696 +13.686 -51.085 }}


{{Optimal ET sequence|legend=1| 3, 6b, 9 }}
{{Optimal ET sequence|legend=1| 3, 6b, 9 }}


[[Badness]] (Smith): 0.059079
[[Badness]] (Sintel): 1.50


=== 11-limit ===
=== 11-limit ===
Line 253: Line 247:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~3/2 = 679.881 (~16/15 = 120.119)
* WE: ~5/4 = 402.1799{{c}}, ~3/2 = 683.7477{{c}} (~16/15 = 120.6120{{c}})
* POTE: ~5/4 = 400.000, ~3/2 = 680.042 (~16/15 = 119.958)
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 680.0162{{c}} (~16/15 = 119.9838{{c}})


{{Optimal ET sequence|legend=0| 3, 9 }}
{{Optimal ET sequence|legend=0| 3, 6b, 9 }}


Badness (Smith): 0.037183
Badness (Sintel): 1.23


== Hexe ==
== Hexe ==
Hexe tempers out 50/49 and may be described as {{nowrap| 6 & 12 }}, viewed as [[6edo|6et]] with an independent generator for prime 3. Its ploidacot is hexaploid monocot.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 268: Line 264:


: mapping generators: ~28/25, ~3
: mapping generators: ~28/25, ~3
{{Multival|legend=1| 6 0 0 -14 -17 0 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~28/25 = 200.000, ~3/2 = 701.955 (~16/15 = 98.045)
* [[WE]]: ~28/25 = 199.0488{{c}}, ~3/2 = 707.5815{{c}} (~25/24 = 88.6137{{c}})
: [[error map]]: {{val| 0.000 0.000 +13.686 +31.174 }}
: [[error map]]: {{val| +5.870 -11.122 +27.382 -34.224 }}
* [[POTE]]: ~28/25 = 200.000, ~3/2 = 710.963 (~16/15 = 89.037)
* [[CWE]]: ~28/25 = 200.0000{{c}}, ~3/2 = 708.6907{{c}} (~25/24 = 91.3093{{c}})
: error map: {{val| 0.000 +9.008 +13.686 +31.174 }}
: error map: {{val| 0.000 +6.735 +13.686 +31.174 }}


{{Optimal ET sequence|legend=1| 6, 12, 30d, 42dd, 54cdd }}
{{Optimal ET sequence|legend=1| 6, 12, 30d, 42dd, 54cdd }}


[[Badness]] (Smith): 0.057730
[[Badness]] (Sintel): 1.46


=== 11-limit ===
=== 11-limit ===
Line 289: Line 283:


Optimal tunings:  
Optimal tunings:  
* CTE: ~28/25 = 200.000, ~3/2 = 701.955 (~16/15 = 98.045)
* WE: ~28/25 = 198.6942{{c}}, ~3/2 = 709.6404{{c}} (~25/24 = 85.1362{{c}})
* POTE: ~28/25 = 200.000, ~3/2 = 714.304 (~16/15 = 85.696)
* CWE: ~28/25 = 200.0000{{c}}, ~3/2 = 711.8043{{c}} (~25/24 = 88.1957{{c}})


{{Optimal ET sequence|legend=0| 6, 12, 30dee, 42ddeee }}
{{Optimal ET sequence|legend=0| 6, 12, 30dee, 42ddeee }}


Badness (Smith): 0.038412
Badness (Sintel): 1.27


=== 13-limit ===
=== 13-limit ===
Line 304: Line 298:


Optimal tunings:  
Optimal tunings:  
* CTE: ~28/25 = 200.000, ~3/2 = 692.433 (~21/20 = 92.433)
* WE: ~28/25 = 198.4492{{c}}, ~3/2 = 704.4994{{c}} (~25/24 = 89.2973{{c}})
* POTE: ~28/25 = 200.000, ~3/2 = 710.005 (~16/15 = 89.995)
* CWE: ~28/25 = 200.0000{{c}}, ~3/2 = 706.6050{{c}} (~16/15 = 93.3950{{c}})


{{Optimal ET sequence|legend=0| 6f, 12f }}
{{Optimal ET sequence|legend=0| 6f, 12f }}


Badness (Smith): 0.035946
Badness (Sintel): 1.49


== Triforce ==
== Triforce ==
[[File:triforce9.jpg|thumb|alt=triforce9.jpg|Lattice of triforce]]
[[File:triforce9.jpg|thumb|alt=triforce9.jpg|Lattice of triforce]]
Triforce tempers out 49/48 and may be described as {{nowrap| 9 & 15 }}. Its ploidacot is triploid alpha-dicot. [[24edo]] and [[39edo]] are among the possible tunings.


[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7
Line 321: Line 317:


: mapping generators: ~5/4, ~7/4
: mapping generators: ~5/4, ~7/4
{{Multival|legend=1| 6 0 3 -14 -12 7 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~7/4 = 952.295 (~35/32 = 152.295)
* [[WE]]: ~5/4 = 399.7480{{c}}, ~7/4 = 952.3507{{c}} (~35/32 = 152.8547{{c}})
: [[error map]]: {{val| 0.000 +2.635 +13.686 -16.531 }}
: [[error map]]: {{val| -0.756 +2.746 +11.922 -17.987 }}
* [[POTE]]: ~5/4 = 400.000, ~7/4 = 952.951 (~35/32 = 152.951)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~7/4 = 952.7463{{c}} (~35/32 = 152.7463{{c}})
: error map: {{val| 0.000 +3.947 +13.686 -15.875 }}
: error map: {{val| 0.000 +3.538 +13.686 -16.080 }}


{{Optimal ET sequence|legend=1| 6, 9, 15, 24, 39 }}
{{Optimal ET sequence|legend=1| 6, 9, 15, 24, 39 }}


[[Badness]] (Smith): 0.054988
[[Badness]] (Sintel): 1.39


=== 11-limit ===
=== 11-limit ===
Line 340: Line 334:


Mapping: {{mapping| 3 0 7 6 8 | 0 2 0 1 1 }}
Mapping: {{mapping| 3 0 7 6 8 | 0 2 0 1 1 }}
Wedgie: {{multival| 6 0 3 3 -14 -12 -16 7 7 -2 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~7/4 = 952.250 (~12/11 = 152.250)
* WE: ~5/4 = 399.7654{{c}}, ~7/4 = 952.3730{{c}} (~12/11 = 152.8421{{c}})
* POTE: ~5/4 = 400.000, ~7/4 = 952.932 (~12/11 = 152.932)
* CWE: ~5/4 = 400.0000{{c}}, ~7/4 = 952.7447{{c}} (~12/11 = 152.7447{{c}})


{{Optimal ET sequence|legend=0| 6, 9, 15, 24, 39 }}
{{Optimal ET sequence|legend=0| 6, 9, 15, 24, 39 }}


Badness (Smith): 0.026152
Badness (Sintel): 0.865


; Music
; Music
* [https://cityoftheasleep.bandcamp.com/track/the-triforce-of-courage-24edo ''The Triforce of Courage (24edo)''] by [[Igliashon Jones]] (2018)
* [https://cityoftheasleep.bandcamp.com/track/the-triforce-of-courage-24edo ''The Triforce of Courage (24edo)'']{{dead link}} by [[Igliashon Jones]] (2018)
* [http://chrisvaisvil.com/2-2-1-2-2-1-2-2-1-mode-of-15-edo/ ''2-2-1-2-2-1-2-2-1 mode of 15 edo''] [http://micro.soonlabel.com/15-ET/20130831_221of15.mp3 play] by [[Chris Vaisvil]]
* [https://www.chrisvaisvil.com/2-2-1-2-2-1-2-2-1-mode-of-15-edo/ ''2-2-1-2-2-1-2-2-1 mode of 15 edo''] [https://web.archive.org/web/20201127015017/http://micro.soonlabel.com/15-ET/20130831_221of15.mp3 play] by [[Chris Vaisvil]] (2013)


==== 13-limit ====
==== 13-limit ====
Line 363: Line 355:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~7/4 = 950.805 (~12/11 = 150.805)
* WE: ~5/4 = 399.7107{{c}}, ~7/4 = 950.9983{{c}} (~12/11 = 151.5768{{c}})
* POTE: ~5/4 = 400.000, ~7/4 = 951.687 (~12/11 = 151.687)
* CWE: ~5/4 = 400.0000{{c}}, ~7/4 = 951.4465{{c}} (~12/11 = 151.4465{{c}})


{{Optimal ET sequence|legend=0| 6, 9, 15, 24 }}
{{Optimal ET sequence|legend=0| 6f, 9, 15, 24 }}


Badness (Smith): 0.020248
Badness (Sintel): 0.837


; Scales
; Scales
Line 374: Line 366:


==== Semitriforce ====
==== Semitriforce ====
This extension splits the period into 1/6-octave for ~44/39. Its ploidacot is hexaploid dicot.
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11.13


Line 383: Line 377:


Optimal tunings:  
Optimal tunings:  
* CTE: ~44/39 = 200.000, ~7/4 = 952.531 (~40/39 = 47.469)
* WE: ~44/39 = 199.8321{{c}}, ~7/4 = 952.5580{{c}} (~40/39 = 46.6024{{c}})
* POTE: ~44/39 = 200.000, ~7/4 = 953.358 (~40/39 = 46.642)
* CWE: ~44/39 = 200.0000{{c}}, ~7/4 = 953.2005{{c}} (~40/39 = 46.7995{{c}})


{{Optimal ET sequence|legend=0| 6, 18bd, 24 }}
{{Optimal ET sequence|legend=0| 6, 18bd, 24 }}


Badness (Smith): 0.059160
Badness (Sintel): 2.44


== Hemiaug ==
== Hemiaug ==
Hemiaug tempers out 245/243 and may be described as {{nowrap| 24 & 27 }}. The generator may be taken as ~14/9, but also a neutral third or a neutral second that stand in for 11/9~16/13 and 12/11~13/12 in the higher limits, respectively. Hemiaug's ploidacot is triploid dicot. [[27edo]] makes for a recommendable tuning in the 7-limit, but [[51edo]] serves better in the higher limits.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 398: Line 394:


: mapping generators: ~5/4, ~14/9
: mapping generators: ~5/4, ~14/9
{{Multival|legend=1| 6 0 15 -14 7 35 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~14/9 = 752.834 (~36/35 = 47.166)
* [[WE]]: ~5/4 = 398.9278{{c}}, ~14/9 = 752.8583{{c}} (~36/35 = 44.9973{{c}})
: [[error map]]: {{val| 0.000 +3.712 +13.686 -4.658 }}
: [[error map]]: {{val| -3.217 +2.689 +6.181 -3.462 }}
* [[POTE]]: ~5/4 = 400.000, ~14/9 = 754.882 (~36/35 = 45.118)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~14/9 = 754.2078{{c}} (~36/35 = 45.7922{{c}})
: error map: {{val| 0.000 +7.808 +13.686 +5.583 }}
: error map: {{val| 0.000 +6.461 +13.686 +2.213 }}


{{Optimal ET sequence|legend=1| 24, 27 }}
{{Optimal ET sequence|legend=1| 24, 27 }}


[[Badness]] (Smith): 0.070463
[[Badness]] (Sintel): 1.78


=== 11-limit ===
=== 11-limit ===
Line 419: Line 413:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~14/9 = 752.051 (~36/35 = 47.949)
* WE: ~5/4 = 398.8946{{c}}, ~14/9 = 752.1272{{c}} (~36/35 = 45.6619{{c}})
* POTE: ~5/4 = 400.000, ~14/9 = 754.212 (~36/35 = 45.788)
* CWE: ~5/4 = 400.0000{{c}}, ~14/9 = 753.5000{{c}} (~36/35 = 46.5000{{c}})


{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}
{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}


Badness (Smith): 0.038232
Badness (Sintel): 1.26


=== 13-limit ===
=== 13-limit ===
Subgroup: 2.3.5.7.11.13
Subgroup: 2.3.5.7.11.13


Comma list: 56/55, 91/90, 128/125, 245/243
Comma list: 56/55, 91/90, 128/125, 243/242


Mapping: {{mapping| 3 1 7 -1 1 13 | 0 2 0 5 5 -1 }}
Mapping: {{mapping| 3 1 7 -1 1 13 | 0 2 0 5 5 -1 }}


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~14/9 = 752.128 (~36/35 = 47.872)
* WE: ~5/4 = 399.1053{{c}}, ~14/9 = 752.0643{{c}} (~36/35 = 46.1463{{c}})
* POTE: ~5/4 = 400.000, ~14/9 = 753.750 (~36/35 = 46.250)
* CWE: ~5/4 = 400.0000{{c}}, ~14/9 = 753.3806{{c}} (~36/35 = 46.6194{{c}})


{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}
{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}


Badness (Smith): 0.030159
Badness (Sintel): 1.25


== Hemiug ==
== Hemiug ==
Hemiug tempers out 1323/1250 and may be described as {{nowrap| 21 & 24 }}. The generator is a similar interval but for ~32/21 instead of ~14/9, and the ploidacot is triploid dicot, the same as hemiaug.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 449: Line 445:


: mapping generators: ~5/4, ~32/21
: mapping generators: ~5/4, ~32/21
{{Multival|legend=1| 6 0 -9 -14 -31 -21 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~32/21 = 747.948 (~21/20 = 52.052)
* [[WE]]: ~5/4 = 400.1805{{c}}, ~32/21 = 748.2436{{c}} (~21/20 = 52.1174{{c}})
: [[error map]]: {{val| 0.000 -6.058 +13.686 -12.671 }}
: [[error map]]: {{val| +0.542 -5.287 +14.950 -11.030 }}
* [[POTE]]: ~5/4 = 400.000, ~32/21 = 747.907 (~21/20 = 52.093)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~32/21 = 747.9138{{c}} (~21/20 = 52.0862{{c}})
: error map: {{val| 0.000 -6.143 +13.686 -12.544 }}
: error map: {{val| 0.000 -6.127 +13.686 -12.567 }}


{{Optimal ET sequence|legend=1| 21, 24, 45c }}
{{Optimal ET sequence|legend=1| 21, 24, 45c }}


[[Badness]] (Smith): 0.137764
[[Badness]] (Sintel): 3.49


=== 11-limit ===
=== 11-limit ===
Line 470: Line 464:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~32/21 = 748.296 (~33/32 = 51.704)
* WE: ~5/4 = 400.0637{{c}}, ~32/21 = 748.4638{{c}} (~33/32 = 51.6637{{c}})
* POTE: ~5/4 = 400.000, ~32/21 = 748.345 (~33/32 = 51.655)
* CWE: ~5/4 = 400.0000{{c}}, ~32/21 = 748.3383{{c}} (~33/32 = 51.6617{{c}})


{{Optimal ET sequence|legend=0| 21, 24 }}
{{Optimal ET sequence|legend=0| 21, 24 }}


Badness (Smith): 0.068062
Badness (Sintel): 2.25


=== 13-limit ===
=== 13-limit ===
Line 485: Line 479:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~32/21 = 748.525 (~33/32 = 51.475)
* WE: ~5/4 = 399.8855{{c}}, ~32/21 = 748.2378{{c}} (~33/32 = 51.5332{{c}})
* POTE: ~5/4 = 400.000, ~32/21 = 748.452 (~33/32 = 51.548)
* CWE: ~5/4 = 400.0000{{c}}, ~32/21 = 748.4655{{c}} (~33/32 = 51.5345{{c}})


{{Optimal ET sequence|legend=0| 21, 24 }}
{{Optimal ET sequence|legend=0| 21, 24 }}


Badness (Smith): 0.042289
Badness (Sintel): 1.75


== Oodako ==
== Oodako ==
Oodako tempers out 2401/2400 and may be described as {{nowrap| 21 & 27 }}. It is generated by a quarter of a fifth, which stands in for ~28/25. Its ploidacot is triploid tetracot.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 500: Line 496:


: mapping generators: ~5/4, ~28/25
: mapping generators: ~5/4, ~28/25
{{Multival|legend=1| 12 0 3 -28 -29 7 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~28/25 = 175.359
* [[WE]]: ~5/4 = 399.0296{{c}}, ~28/25 = 176.2174{{c}} (~49/48 = 46.5949{{c}})
: [[error map]]: {{val| 0.000 -0.521 +13.686 +6.533 }}
: [[error map]]: {{val| -2.911 +0.004 +6.894 -0.371 }}
* [[POTE]]: ~5/4 = 400.000, ~28/25 = 176.646
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~28/25 = 176.2984{{c}} (~49/48 = 47.4031{{c}})
: error map: {{val| 0.000 +4.629 +13.686 +7.820 }}
: error map: {{val| 0.000 +3.239 +13.686 +7.473 }}


{{Optimal ET sequence|legend=1| 6, 21, 27, 75c, 102ccd, 129bccd }}
{{Optimal ET sequence|legend=1| 6, 21, 27, 75c, 102ccd, 129bccd }}


[[Badness]] (Smith): 0.113209
[[Badness]] (Sintel): 2.86


=== 11-limit ===
=== 11-limit ===
Line 521: Line 515:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~11/10 = 175.053
* WE: ~5/4 = 398.6615{{c}}, ~11/10 = 176.3886{{c}} (~49/48 = 45.8843{{c}})
* POTE: ~5/4 = 400.000, ~11/10 = 176.981
* CWE: ~5/4 = 400.0000{{c}}, ~11/10 = 176.5471{{c}} (~49/48 = 46.9059{{c}})


{{Optimal ET sequence|legend=0| 6, 21, 27e }}
{{Optimal ET sequence|legend=0| 6, 21, 27e }}


Badness (Smith): 0.059192
Badness (Sintel): 1.96


=== 13-limit ===
=== 13-limit ===
Line 536: Line 530:


Optimal tunings:  
Optimal tunings:  
* CTE: ~5/4 = 400.000, ~11/10 = 175.252
* WE: ~5/4 = 398.8612{{c}}, ~11/10 = 176.0486{{c}} (~49/48 = 46.7640{{c}})
* POTE: ~5/4 = 400.000, ~11/10 = 176.551
* CWE: ~5/4 = 400.0000{{c}}, ~11/10 = 176.3326{{c}} (~49/48 = 47.3348{{c}})


{{Optimal ET sequence|legend=0| 6, 21, 27e }}
{{Optimal ET sequence|legend=0| 6, 21, 27e }}


Badness (Smith): 0.042323
Badness (Sintel): 1.75


== Hemisemiaug ==
== Hemisemiaug ==
Hemisemiaug tempers out 12005/11664 and splits both the period and generator of augmented in two. Its ploidacot is hexaploid alpha-dicot.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 551: Line 547:


: mapping generators: ~54/49, ~45/28
: mapping generators: ~54/49, ~45/28
{{Multival|legend=1| 12 0 18 -28 -5 42 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~54/49 = 200.000, ~45/28 = 853.190 (~36/35 = 53.190)
* [[WE]]: ~54/49 = 199.5469{{c}}, ~45/28 = 853.5468{{c}} (~36/35 = 55.3594{{c}})
: [[error map]]: {{val| 0.000 +4.425 +13.686 -9.256 }}
: [[error map]]: {{val| -2.719 +4.686 +7.342 -9.998 }}
* [[POTE]]: ~54/49 = 200.000, ~45/28 = 855.485 (~36/35 = 55.485)
* [[CWE]]: ~54/49 = 200.0000{{c}}, ~45/28 = 854.7144{{c}} (~36/35 = 54.7144{{c}})
: error map: {{val| 0.000 +9.015 +13.686 -2.371 }}
: error map: {{val| 0.000 +7.474 +13.686 -4.683 }}


{{Optimal ET sequence|legend=1| 18, 24, 42 }}
{{Optimal ET sequence|legend=1| 18, 24, 42 }}


[[Badness]] (Smith): 0.210984
[[Badness]] (Sintel): 5.34


=== 11-limit ===
=== 11-limit ===
Line 572: Line 566:


Optimal tunings:  
Optimal tunings:  
* CTE: ~54/49 = 200.000, ~18/11 = 852.597 (~36/35 = 52.597)
* WE: ~54/49 = 199.5188{{c}}, ~18/11 = 853.1623{{c}} (~36/35 = 55.0872{{c}})
* POTE: ~54/49 = 200.000, ~18/11 = 855.220 (~36/35 = 55.220)
* CWE: ~54/49 = 200.0000{{c}}, ~18/11 = 854.3545{{c}} (~36/35 = 54.3545{{c}})


{{Optimal ET sequence|legend=0| 24, 42e, 66ce, 108bccee }}
{{Optimal ET sequence|legend=0| 18e, 24, 42e, 66ce, 108bccee }}


Badness (Smith): 0.080738
Badness (Sintel): 2.67


== Niner ==
== Niner ==
Niner gives 9 as the complexity of an otonal tetrad, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads.
Niner tempers out 686/675 and may be described as the {{nowrap| 9 & 27 }} temperament. Its ploidacot is enneaploid monocot. It gives 9 as the complexity of a [[harmonic seventh chord]], tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads. 27edo, [[36edo]] and [[63edo]] in the 63c val are among the possible tunings.  


[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7
Line 589: Line 583:


: mapping generators: ~49/45, ~3
: mapping generators: ~49/45, ~3
{{Multival|legend=1| 9 0 9 -21 -11 21 }}


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~49/45 = 133.333, ~3/2 = 702.004 (~36/35 = 35.338)
* [[WE]]: ~49/45 = 133.0272{{c}}, ~3/2 = 705.5438{{c}} (~36/35 = 40.4075{{c}})
: [[error map]]: {{val| 0.000 +0.049 +13.686 -0.155 }}
: [[error map]]: {{val| -2.755 +0.834 +7.259 -2.737 }}
* [[POTE]]: ~49/45 = 133.333, ~3/2 = 707.167 (~36/35 = 40.501)
* [[CWE]]: ~49/45 = 133.3333{{c}}, ~3/2 = 705.5157{{c}} (~36/35 = 38.8490{{c}})
: error map: {{val| 0.000 +5.212 +13.686 +5.008 }}
: error map: {{val| 0.000 +3.561 +13.686 +3.356 }}


{{Optimal ET sequence|legend=1| 9, 18, 27, 63c, 90cc }}
{{Optimal ET sequence|legend=1| 9, 18, 27, 63c, 90cc }}


[[Badness]] (Smith): 0.067157
[[Badness]] (Sintel): 1.70


=== 11-limit ===
=== 11-limit ===
Line 610: Line 602:


Optimal tunings:  
Optimal tunings:  
* CTE: ~12/11 = 133.333, ~3/2 = 699.622 (~36/35 = 32.955)
* WE: ~12/11 = 132.9553{{c}}, ~3/2 = 704.7217{{c}} (~36/35 = 39.9453{{c}})
* POTE: ~12/11 = 133.333, ~3/2 = 706.726 (~36/35 = 40.059)
* CWE: ~12/11 = 133.3333{{c}}, ~3/2 = 704.5723{{c}} (~36/35 = 37.9056{{c}})


{{Optimal ET sequence|legend=0| 9, 18e, 27e, 63cee }}
{{Optimal ET sequence|legend=0| 9, 18e, 27e, 63cee }}


Badness (Smith): 0.034861
Badness (Sintel): 1.15


=== 13-limit ===
=== 13-limit ===
Line 625: Line 617:


Optimal tunings:  
Optimal tunings:  
* CTE: ~14/13 = 133.333, ~3/2 = 700.433 (~36/35 = 33.766)
* WE: ~14/13 = 133.0143{{c}}, ~3/2 = 705.1969{{c}} (~36/35 = 40.1256{{c}})
* POTE: ~14/13 = 133.333, ~3/2 = 706.889 (~36/35 = 40.222)
* CWE: ~14/13 = 133.3333{{c}}, ~3/2 = 705.0176{{c}} (~36/35 = 38.3510{{c}})


{{Optimal ET sequence|legend=0| 9, 18e, 27e }}
{{Optimal ET sequence|legend=0| 9, 18e, 27e }}


Badness (Smith): 0.024143
Badness (Sintel): 0.998


== Trug ==
== Trug ==
Trug tempers out 360/343. It is generated by an interval of ~48/35, tuned very close to a perfect fourth, but the perfect fourth is mapped to three generator steps and a period. Its ploidacot is triploid alpha-tricot. 12edo is about as accurate as it can be tuned.
[[Subgroup]]: 2.3.5.7
[[Subgroup]]: 2.3.5.7


Line 642: Line 636:


[[Optimal tuning]]s:  
[[Optimal tuning]]s:  
* [[CTE]]: ~5/4 = 400.000, ~48/35 = 498.637 (~15/14 = 98.637)
* [[WE]]: ~5/4 = 398.2337{{c}}, ~48/35 = 499.7635{{c}} (~15/14 = 101.5299{{c}})
: [[error map]]: {{val| 0.000 -6.045 +13.686 +28.447 }}
: [[error map]]: {{val| -2.755 +0.834 +7.259 -2.737 }}
* [[POTE]]: ~5/4 = 400.000, ~48/35 = 501.980 (~15/14 = 101.980)
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~48/35 = 500.9654{{c}} (~15/14 = 100.9654{{c}})
: error map: {{val| 0.000 +3.986 +13.686 +35.134 }}
: error map: {{val| 0.000 +3.561 +13.686 +3.356 }}


{{Optimal ET sequence|legend=1| 9bd, 12 }}
{{Optimal ET sequence|legend=1| 3b, 9bd, 12 }}


[[Badness]] (Smith): 0.138279
[[Badness]] (Sintel): 3.50


== External links ==
== External links ==
* [https://www.prismnet.com/~hmiller/music/temp-augmented.html Herman Miller's page about augmented temperament] {{dead link}}
* [https://web.archive.org/web/20211201070113/https://www.prismnet.com/~hmiller/music/temp-augmented.html Herman Miller's page about augmented temperament]


[[Category:Temperament families]]
[[Category:Temperament families]]
[[Category:Pages with mostly numerical content]]
[[Category:Augmented family| ]] <!-- main article -->
[[Category:Augmented family| ]] <!-- main article -->
[[Category:Rank 2]]
[[Category:Rank 2]]

Latest revision as of 16:58, 21 August 2025

This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.

The augmented family of temperaments tempers out the diesis a.k.a. augmented comma, 128/125, the amount by which three 5/4 major thirds fall short of an octave, and so identifies the major third with the 1/3-octave. Hence it has the same 400-cent 5/4-approximations as 12edo.

Augmented

The period is 1/3 octave, and this is what is used for 5/4, the classical major third. The generator can be taken as a fifth or a semitone, and 12edo, with its excellent fifth, is an obvious tuning for 5-limit augmented, though a sharper fifth might be preferred to go with the sharp third. Its ploidacot is triploid monocot.

Subgroup: 2.3.5

Comma list: 128/125

Mapping: [⟨3 0 7], ⟨0 1 0]]

mapping generators: ~5/4, ~3

Optimal tunings:

  • WE: ~5/4 = 399.0128 ¢, ~3/2 = 704.8937 ¢ (~16/15 = 93.1320 ¢)
error map: ⟨-2.962 -0.023 +6.776]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 705.0691 ¢ (~16/15 = 94.9309 ¢)
error map: ⟨0.000 +3.114 +13.686]

Optimal ET sequence: 3, 9, 12, 27, 39, 51c, 90cc

Badness (Sintel): 0.523

Overview to extensions

The second comma of the normal comma list defines which 7-limit family member we are looking at. Augene adds 64/63, august 36/35, hexe 256/245, hemiaug 245/243, and triforce 49/48. Hexe splits the period to 1/6 octave, and hemiaug the generator, giving quartertones instead of semitones.

Augene

Main article: Augene

Augene tempers out 64/63 and 126/125. It may be described as the 12 & 15 temperament. 27edo and 39edo in the 39d val make for good tunings.

Subgroup: 2.3.5.7

Comma list: 64/63, 126/125

Mapping: [⟨3 0 7 18], ⟨0 1 0 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.7461 ¢, ~3/2 = 707.0335 ¢ (~21/20 = 90.4587 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 709.3249 ¢ (~21/20 = 90.6751 ¢)
error map: ⟨0.000 +7.370 +13.686 +12.524]

Optimal ET sequence: 12, 27, 39d, 66cd

Badness (Sintel): 0.628

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 64/63, 100/99

Mapping: [⟨3 0 7 18 20], ⟨0 1 0 -2 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.4962 ¢, ~3/2 = 708.5030 ¢ (~21/20 = 88.4895 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 711.6031 ¢ (~21/20 = 88.3969 ¢)

Optimal ET sequence: 12, 15, 27e

Badness (Sintel): 0.648

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 40/39, 56/55, 64/63, 66/65

Mapping: [⟨3 0 7 18 20 16], ⟨0 1 0 -2 -2 -1]]

Optimal tunings:

  • WE: ~5/4 = 398.0488 ¢, ~3/2 = 708.5402 ¢ (~21/20 = 87.5574 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.6704 ¢ (~21/20 = 87.3296 ¢)

Optimal ET sequence: 12f, 15, 27eff

Badness (Sintel): 0.859

Ogene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 91/90, 100/99

Mapping: [⟨3 0 7 18 20 -8], ⟨0 1 0 -2 -2 4]]

Optimal tunings:

  • WE: ~5/4 = 398.6473 ¢, ~3/2 = 710.1987 ¢ (~21/20 = 87.0959 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.5057 ¢ (~21/20 = 87.4943 ¢)

Optimal ET sequence: 12, 15, 27e, 69bceef

Badness (Sintel): 0.946

Agene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 78/77, 100/99

Mapping: [⟨3 0 7 18 20 35], ⟨0 1 0 -2 -2 -5]]

Optimal tunings:

  • WE: ~5/4 = 398.5229 ¢, ~3/2 = 707.0562 ¢ (~21/20 = 89.9897 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 710.1903 ¢ (~21/20 = 89.8097 ¢)

Optimal ET sequence: 12f, 27e, 66cdeeef

Badness (Sintel): 0.955

Eugene

Subgroup: 2.3.5.7.11

Comma list: 55/54, 64/63, 77/75

Mapping: [⟨3 0 7 18 -4], ⟨0 1 0 -2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.1743 ¢, ~3/2 = 712.6763 ¢ (~21/20 = 85.6723 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 713.9414 ¢ (~21/20 = 86.0586 ¢)

Optimal ET sequence: 12e, 15, 27, 42

Badness (Sintel): 1.18

August

August tempers out 36/35 and 225/224. It may be described as the 9 & 12 temperament. Unlike augene, august calls for a flat tuning of the fifth, and besides 12edo, 21edo is among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 36/35, 128/125

Mapping: [⟨3 0 7 -1], ⟨0 1 0 2]]

Optimal tunings:

  • WE: ~5/4 = 399.1036 ¢, ~3/2 = 694.4509 ¢ (~16/15 = 103.7564 ¢)
error map: ⟨-2.689 -10.193 +7.412 +15.594]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 694.6812 ¢ (~16/15 = 105.3188 ¢)
error map: ⟨0.000 -7.274 +13.686 +20.537]

Optimal ET sequence: 9, 12, 45cd

Badness (Sintel): 0.670

11-limit

Subgroup: 2.3.5.7.11

Comma list: 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1], ⟨0 1 0 2 2]]

Optimal tunings:

  • WE: ~5/4 = 398.9225 ¢, ~3/2 = 690.6486 ¢ (~16/15 = 107.1966 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 690.8519 ¢ (~16/15 = 109.1481 ¢)

Optimal ET sequence: 9, 12, 21, 33e

Badness (Sintel): 0.668

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 27/26, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 -3], ⟨0 1 0 2 2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.0956 ¢, ~3/2 = 687.2261 ¢ (~16/15 = 110.9651 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 687.5057 ¢ (~16/15 = 112.4943 ¢)

Optimal ET sequence: 9, 12f, 21, 33ef

Badness (Sintel): 0.762

Augustus

Subgroup: 2.3.5.7.11.13

Comma list: 26/25, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 11], ⟨0 1 0 2 2 0]]

Optimal tunings:

  • WE: ~5/4 = 400.4230 ¢, ~3/2 = 686.0809 ¢ (~16/15 = 114.7650 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 685.8446 ¢ (~16/15 = 114.1554 ¢)

Optimal ET sequence: 9, 12

Badness (Sintel): 0.919

Inflated

Subgroup: 2.3.5.7

Comma list: 28/27, 128/125

Mapping: [⟨3 0 7 -6], ⟨0 1 0 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4023 ¢, ~3/2 = 719.8327 ¢ (~25/24 = 76.9719 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 721.0196 ¢ (~25/24 = 78.9804 ¢)
error map: ⟨0.000 +19.065 +13.686 -5.767]

Optimal ET sequence: 3d, 12d, 15

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 28/27, 55/54, 128/125

Mapping: [⟨3 0 7 -6 -4], ⟨0 1 0 3 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4016 ¢, ~3/2 = 719.7758 ¢ (~25/24 = 77.0275 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 720.9386 ¢ (~25/24 = 79.0614 ¢)

Optimal ET sequence: 3de, 12de, 15

Badness (Sintel): 1.03

Deflated

Subgroup: 2.3.5.7

Comma list: 21/20, 128/125

Mapping: [⟨3 0 7 13], ⟨0 1 0 -1]]

Optimal tunings:

  • WE: ~5/4 = 401.9566 ¢, ~3/2 = 684.9634 ¢ (~16/15 = 118.9497 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 682.2587 ¢ (~16/15 = 117.7413 ¢)
error map: ⟨0.000 -19.696 +13.686 -51.085]

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.50

11-limit

Subgroup: 2.3.5.7.11

Comma list: 21/20, 33/32, 128/125

Mapping: [⟨3 0 7 13 15], ⟨0 1 0 -1 -1]]

Optimal tunings:

  • WE: ~5/4 = 402.1799 ¢, ~3/2 = 683.7477 ¢ (~16/15 = 120.6120 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 680.0162 ¢ (~16/15 = 119.9838 ¢)

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.23

Hexe

Hexe tempers out 50/49 and may be described as 6 & 12, viewed as 6et with an independent generator for prime 3. Its ploidacot is hexaploid monocot.

Subgroup: 2.3.5.7

Comma list: 50/49, 128/125

Mapping: [⟨6 0 14 17], ⟨0 1 0 0]]

mapping generators: ~28/25, ~3

Optimal tunings:

  • WE: ~28/25 = 199.0488 ¢, ~3/2 = 707.5815 ¢ (~25/24 = 88.6137 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 708.6907 ¢ (~25/24 = 91.3093 ¢)
error map: ⟨0.000 +6.735 +13.686 +31.174]

Optimal ET sequence: 6, 12, 30d, 42dd, 54cdd

Badness (Sintel): 1.46

11-limit

Subgroup: 2.3.5.7.11

Comma list: 50/49, 56/55, 125/121

Mapping: [⟨6 0 14 17 21], ⟨0 1 0 0 0]]

Optimal tunings:

  • WE: ~28/25 = 198.6942 ¢, ~3/2 = 709.6404 ¢ (~25/24 = 85.1362 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 711.8043 ¢ (~25/24 = 88.1957 ¢)

Optimal ET sequence: 6, 12, 30dee, 42ddeee

Badness (Sintel): 1.27

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 50/49, 56/55, 66/65, 105/104

Mapping: [⟨6 0 14 17 21 13], ⟨0 1 0 0 0 1]]

Optimal tunings:

  • WE: ~28/25 = 198.4492 ¢, ~3/2 = 704.4994 ¢ (~25/24 = 89.2973 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 706.6050 ¢ (~16/15 = 93.3950 ¢)

Optimal ET sequence: 6f, 12f

Badness (Sintel): 1.49

Triforce

triforce9.jpg
Lattice of triforce

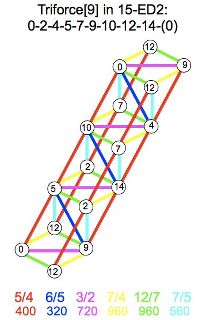
Triforce tempers out 49/48 and may be described as 9 & 15. Its ploidacot is triploid alpha-dicot. 24edo and 39edo are among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 49/48, 128/125

Mapping: [⟨3 0 7 6], ⟨0 2 0 1]]

mapping generators: ~5/4, ~7/4

Optimal tunings:

  • WE: ~5/4 = 399.7480 ¢, ~7/4 = 952.3507 ¢ (~35/32 = 152.8547 ¢)
error map: ⟨-0.756 +2.746 +11.922 -17.987]
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7463 ¢ (~35/32 = 152.7463 ¢)
error map: ⟨0.000 +3.538 +13.686 -16.080]

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 49/48, 56/55, 77/75

Mapping: [⟨3 0 7 6 8], ⟨0 2 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 399.7654 ¢, ~7/4 = 952.3730 ¢ (~12/11 = 152.8421 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7447 ¢ (~12/11 = 152.7447 ¢)

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 0.865

Music

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 66/65, 77/75

Mapping: [⟨3 0 7 6 8 4], ⟨0 2 0 1 1 3]]

Optimal tunings:

  • WE: ~5/4 = 399.7107 ¢, ~7/4 = 950.9983 ¢ (~12/11 = 151.5768 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 951.4465 ¢ (~12/11 = 151.4465 ¢)

Optimal ET sequence: 6f, 9, 15, 24

Badness (Sintel): 0.837

Scales
  • triphi, Triforce[9] with L:s = phi

Semitriforce

This extension splits the period into 1/6-octave for ~44/39. Its ploidacot is hexaploid dicot.

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 77/75, 507/500

Mapping: [⟨6 0 14 12 16 27], ⟨0 2 0 1 1 -1]]

mapping generators: ~44/39, ~7/4

Optimal tunings:

  • WE: ~44/39 = 199.8321 ¢, ~7/4 = 952.5580 ¢ (~40/39 = 46.6024 ¢)
  • CWE: ~44/39 = 200.0000 ¢, ~7/4 = 953.2005 ¢ (~40/39 = 46.7995 ¢)

Optimal ET sequence: 6, 18bd, 24

Badness (Sintel): 2.44

Hemiaug

Hemiaug tempers out 245/243 and may be described as 24 & 27. The generator may be taken as ~14/9, but also a neutral third or a neutral second that stand in for 11/9~16/13 and 12/11~13/12 in the higher limits, respectively. Hemiaug's ploidacot is triploid dicot. 27edo makes for a recommendable tuning in the 7-limit, but 51edo serves better in the higher limits.

Subgroup: 2.3.5.7

Comma list: 128/125, 245/243

Mapping: [⟨3 1 7 -1], ⟨0 2 0 5]]

mapping generators: ~5/4, ~14/9

Optimal tunings:

  • WE: ~5/4 = 398.9278 ¢, ~14/9 = 752.8583 ¢ (~36/35 = 44.9973 ¢)
error map: ⟨-3.217 +2.689 +6.181 -3.462]
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 754.2078 ¢ (~36/35 = 45.7922 ¢)
error map: ⟨0.000 +6.461 +13.686 +2.213]

Optimal ET sequence: 24, 27

Badness (Sintel): 1.78

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 243/242

Mapping: [⟨3 1 7 -1 1], ⟨0 2 0 5 5]]

Optimal tunings:

  • WE: ~5/4 = 398.8946 ¢, ~14/9 = 752.1272 ¢ (~36/35 = 45.6619 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.5000 ¢ (~36/35 = 46.5000 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.26

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 91/90, 128/125, 243/242

Mapping: [⟨3 1 7 -1 1 13], ⟨0 2 0 5 5 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.1053 ¢, ~14/9 = 752.0643 ¢ (~36/35 = 46.1463 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.3806 ¢ (~36/35 = 46.6194 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.25

Hemiug

Hemiug tempers out 1323/1250 and may be described as 21 & 24. The generator is a similar interval but for ~32/21 instead of ~14/9, and the ploidacot is triploid dicot, the same as hemiaug.

Subgroup: 2.3.5.7

Comma list: 128/125, 1323/1250

Mapping: [⟨3 1 7 14], ⟨0 2 0 -3]]

mapping generators: ~5/4, ~32/21

Optimal tunings:

  • WE: ~5/4 = 400.1805 ¢, ~32/21 = 748.2436 ¢ (~21/20 = 52.1174 ¢)
error map: ⟨+0.542 -5.287 +14.950 -11.030]
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 747.9138 ¢ (~21/20 = 52.0862 ¢)
error map: ⟨0.000 -6.127 +13.686 -12.567]

Optimal ET sequence: 21, 24, 45c

Badness (Sintel): 3.49

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 1323/1250

Mapping: [⟨3 1 7 14 16], ⟨0 2 0 -3 -3]]

Optimal tunings:

  • WE: ~5/4 = 400.0637 ¢, ~32/21 = 748.4638 ¢ (~33/32 = 51.6637 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.3383 ¢ (~33/32 = 51.6617 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 2.25

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 66/65, 105/104, 507/500

Mapping: [⟨3 1 7 14 16 13], ⟨0 2 0 -3 -3 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.8855 ¢, ~32/21 = 748.2378 ¢ (~33/32 = 51.5332 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.4655 ¢ (~33/32 = 51.5345 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 1.75

Oodako

Oodako tempers out 2401/2400 and may be described as 21 & 27. It is generated by a quarter of a fifth, which stands in for ~28/25. Its ploidacot is triploid tetracot.

Subgroup: 2.3.5.7

Comma list: 128/125, 2401/2400

Mapping: [⟨3 3 7 8], ⟨0 4 0 1]]

mapping generators: ~5/4, ~28/25

Optimal tunings:

  • WE: ~5/4 = 399.0296 ¢, ~28/25 = 176.2174 ¢ (~49/48 = 46.5949 ¢)
error map: ⟨-2.911 +0.004 +6.894 -0.371]
  • CWE: ~5/4 = 400.0000 ¢, ~28/25 = 176.2984 ¢ (~49/48 = 47.4031 ¢)
error map: ⟨0.000 +3.239 +13.686 +7.473]

Optimal ET sequence: 6, 21, 27, 75c, 102ccd, 129bccd

Badness (Sintel): 2.86

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 2401/2400

Mapping: [⟨3 3 7 8 10], ⟨0 4 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 398.6615 ¢, ~11/10 = 176.3886 ¢ (~49/48 = 45.8843 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.5471 ¢ (~49/48 = 46.9059 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.96

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 128/125, 507/500

Mapping: [⟨3 3 7 8 10 12], ⟨0 4 0 1 1 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.8612 ¢, ~11/10 = 176.0486 ¢ (~49/48 = 46.7640 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.3326 ¢ (~49/48 = 47.3348 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.75

Hemisemiaug

Hemisemiaug tempers out 12005/11664 and splits both the period and generator of augmented in two. Its ploidacot is hexaploid alpha-dicot.

Subgroup: 2.3.5.7

Comma list: 128/125, 12005/11664

Mapping: [⟨6 1 14 4], ⟨0 2 0 3]]

mapping generators: ~54/49, ~45/28

Optimal tunings:

  • WE: ~54/49 = 199.5469 ¢, ~45/28 = 853.5468 ¢ (~36/35 = 55.3594 ¢)
error map: ⟨-2.719 +4.686 +7.342 -9.998]
  • CWE: ~54/49 = 200.0000 ¢, ~45/28 = 854.7144 ¢ (~36/35 = 54.7144 ¢)
error map: ⟨0.000 +7.474 +13.686 -4.683]

Optimal ET sequence: 18, 24, 42

Badness (Sintel): 5.34

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 3773/3645

Mapping: [⟨6 1 14 4 8], ⟨0 2 0 3 3]]

Optimal tunings:

  • WE: ~54/49 = 199.5188 ¢, ~18/11 = 853.1623 ¢ (~36/35 = 55.0872 ¢)
  • CWE: ~54/49 = 200.0000 ¢, ~18/11 = 854.3545 ¢ (~36/35 = 54.3545 ¢)

Optimal ET sequence: 18e, 24, 42e, 66ce, 108bccee

Badness (Sintel): 2.67

Niner

Niner tempers out 686/675 and may be described as the 9 & 27 temperament. Its ploidacot is enneaploid monocot. It gives 9 as the complexity of a harmonic seventh chord, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads. 27edo, 36edo and 63edo in the 63c val are among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 128/125, 686/675

Mapping: [⟨9 0 21 11], ⟨0 1 0 1]]

mapping generators: ~49/45, ~3

Optimal tunings:

  • WE: ~49/45 = 133.0272 ¢, ~3/2 = 705.5438 ¢ (~36/35 = 40.4075 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~49/45 = 133.3333 ¢, ~3/2 = 705.5157 ¢ (~36/35 = 38.8490 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 9, 18, 27, 63c, 90cc

Badness (Sintel): 1.70

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 540/539

Mapping: [⟨9 0 21 11 17], ⟨0 1 0 1 1]]

Optimal tunings:

  • WE: ~12/11 = 132.9553 ¢, ~3/2 = 704.7217 ¢ (~36/35 = 39.9453 ¢)
  • CWE: ~12/11 = 133.3333 ¢, ~3/2 = 704.5723 ¢ (~36/35 = 37.9056 ¢)

Optimal ET sequence: 9, 18e, 27e, 63cee

Badness (Sintel): 1.15

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 91/90, 128/125

Mapping: [⟨9 0 21 11 17 19], ⟨0 1 0 1 1 1]]

Optimal tunings:

  • WE: ~14/13 = 133.0143 ¢, ~3/2 = 705.1969 ¢ (~36/35 = 40.1256 ¢)
  • CWE: ~14/13 = 133.3333 ¢, ~3/2 = 705.0176 ¢ (~36/35 = 38.3510 ¢)

Optimal ET sequence: 9, 18e, 27e

Badness (Sintel): 0.998

Trug

Trug tempers out 360/343. It is generated by an interval of ~48/35, tuned very close to a perfect fourth, but the perfect fourth is mapped to three generator steps and a period. Its ploidacot is triploid alpha-tricot. 12edo is about as accurate as it can be tuned.

Subgroup: 2.3.5.7

Comma list: 128/125, 360/343

Mapping: [⟨3 1 7 6], ⟨0 3 0 2]]

mapping generators: ~5/4, ~48/35

Optimal tunings:

  • WE: ~5/4 = 398.2337 ¢, ~48/35 = 499.7635 ¢ (~15/14 = 101.5299 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~5/4 = 400.0000 ¢, ~48/35 = 500.9654 ¢ (~15/14 = 100.9654 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 3b, 9bd, 12

Badness (Sintel): 3.50

External links

Retrieved from "https://en.xen.wiki/index.php?title=Augmented_family&oldid=207920"