Augmented family: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Wikispaces>hstraub
**Imported revision 622276421 - Original comment: **
Intro to some of these temps
 
(53 intermediate revisions by 15 users not shown)
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
{{Interwiki
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
| en = Augmented family
: This revision was by author [[User:hstraub|hstraub]] and made on <tt>2017-11-23 15:46:12 UTC</tt>.<br>
| de = Übermässige Temperaturen
: The original revision id was <tt>622276421</tt>.<br>
}}
: The revision comment was: <tt></tt><br>
{{Technical data page}}
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
The '''augmented family''' of [[regular temperament|temperaments]] [[tempering out|tempers out]] the diesis a.k.a. augmented comma, [[128/125]], the amount by which three [[5/4]] major thirds fall short of an [[2/1|octave]], and so identifies the major third with the 1/3-octave. Hence it has the same 400-cent 5/4-approximations as [[12edo]].  
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">&lt;span style="display: block; text-align: right;"&gt;[[toc]]
[[xenharmonie/übermässige Temperaturen|Deutsch]]
&lt;/span&gt;
The 5-limit parent comma for the **augmented family** is 128/125, the [[128_125|diesis]]. Its [[monzo]] is |7 0 -3&gt;, and flipping that yields &lt;&lt;3 0 -7|| for the [[wedgie]]. Hence the period is 1/3 octave, and this is what is used for a major third. The [[generator]] can be taken as a fifth or a semitone, and [[12edo]], with its excellent fifth, is an obvious tuning for [[5-limit]] augmented, though a sharper fifth might be preferred to go with the sharp third.


=Seven limit children=  
== Augmented ==
The second comma of the [[Normal lists|normal comma list]] defines which [[7-limit]] family member we are looking at. August adds 36/35, augene 64/63, hexe 256/245, hemiaug 245/243, and hemis 49/48. Hexe splits the period to 1/6 octave, and hemiaug the generator, giving quarter-tones instead of semitones.
The [[period]] is 1/3 octave, and this is what is used for 5/4, the classical major third. The [[generator]] can be taken as a fifth or a semitone, and [[12edo]], with its excellent fifth, is an obvious tuning for [[5-limit]] augmented, though a sharper fifth might be preferred to go with the sharp third. Its [[ploidacot]] is triploid monocot.  


=August=
[[Subgroup]]: 2.3.5
[[Comma]]s: 36/35, 128/125


[[POTE tuning|POTE generator]]: 696.011
[[Comma list]]: 128/125


[[Map]]: [&lt;3 0 7 -1|, &lt;0 1 0 2|]
{{Mapping|legend=1| 3 0 7 | 0 1 0 }}
[[Wedgie]]: &lt;&lt;3 0 6 -7 1 14||
[[edo|EDOs]]: [[9edo|9]], [[12edo|12]], [[45edo|45cd]], [[57edo|57cd]], [[69edo|69cd]]
[[Badness]]: 0.0265


==11-limit==
: mapping generators: ~5/4, ~3
Commas: 36/35, 45/44, 56/55


POTE generator: ~3/2 = 692.514
[[Optimal tuning]]s:
* [[WE]]: ~5/4 = 399.0128{{c}}, ~3/2 = 704.8937{{c}} (~16/15 = 93.1320{{c}})
: [[error map]]: {{val| -2.962 -0.023 +6.776 }}
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 705.0691{{c}} (~16/15 = 94.9309{{c}})
: error map: {{val| 0.000 +3.114 +13.686 }}


Map: [&lt;3 0 7 -1 1|, &lt;0 1 0 2 2|]
{{Optimal ET sequence|legend=1| 3, 9, 12, 27, 39, 51c, 90cc }}
EDOs: 9, 12, [[21edo|21]], [[33edo|33e]], [[45edo|45cde]]
Badness: 0.0202


==13-limit==
[[Badness]] (Sintel): 0.523
Commas: 27/26, 36/35, 45/44, 56/55


POTE generator: ~3/2 = 688.783
=== Overview to extensions ===
The second comma of the [[Normal lists #Normal interval list|normal comma list]] defines which [[7-limit]] family member we are looking at. Augene adds [[64/63]], august [[36/35]], hexe [[256/245]], hemiaug [[245/243]], and triforce [[49/48]]. Hexe splits the [[period]] to 1/6 octave, and hemiaug the [[generator]], giving quartertones instead of semitones.


Map: [&lt;3 0 7 -1 1 -3|, &lt;0 1 0 2 2 3|]
== Augene ==
EDOs: 9, 12, [[21edo|21]], [[33edo|33ef]], [[54edo|54bcef]]
{{Main| Augene }}
Badness: 0.0184


==Augustus==
Augene tempers out 64/63 and 126/125. It may be described as the {{nowrap| 12 & 15 }} temperament. [[27edo]] and [[39edo]] in the 39d val make for good tunings.
Commas: 26/25, 36/35, 45/44, 56/55


POTE generator: ~3/2 = 685.356
[[Subgroup]]: 2.3.5.7


Map: [&lt;3 0 7 -1 1 11|, &lt;0 1 0 2 2 0|]
[[Comma list]]: 64/63, 126/125
EDOs: 9, 12, 21f
Badness: 0.0222


=Augene=
{{Mapping|legend=1| 3 0 7 18 | 0 1 0 -2 }}
Commas: 64/63, 126/125


[[POTE tuning|POTE generator]]: 709.257
[[Optimal tuning]]s:
* [[WE]]: ~5/4 = 398.7461{{c}}, ~3/2 = 707.0335{{c}} (~21/20 = 90.4587{{c}})
: [[error map]]: {{val| -3.762 +1.317 +4.909 +2.060 }}
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 709.3249{{c}} (~21/20 = 90.6751{{c}})
: error map: {{val| 0.000 +7.370 +13.686 +12.524 }}


Map: [&lt;3 0 7 18|, &lt;0 1 0 -2|]
{{Optimal ET sequence|legend=1| 12, 27, 39d, 66cd }}
Wedgie: &lt;&lt;3 0 -6 -7 -18 -14||
EDOs: [[12edo|12]], [[27edo|27]], [[39edo|39d]], [[66edo|66cd]]
Badness: 0.0248


==11-limit==
[[Badness]] (Sintel): 0.628
Commas: 56/55, 64/63, 100/99


POTE generator: ~3/2 = 711.177
=== 11-limit ===
Subgroup: 2.3.5.7.11


Map: [&lt;3 0 7 18 20|, &lt;0 1 0 -2 -2|]
Comma list: 56/55, 64/63, 100/99
EDOs: 12, 15, 27e
Badness: 0.0196


===13-limit===
Mapping: {{mapping| 3 0 7 18 20 | 0 1 0 -2 -2 }}
Commas: 40/39, 56/55, 64/63, 66/65


POTE generator: ~3/2 = 712.013
Optimal tunings:  
* WE: ~5/4 = 398.4962{{c}}, ~3/2 = 708.5030{{c}} (~21/20 = 88.4895{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 711.6031{{c}} (~21/20 = 88.3969{{c}})


Map: [&lt;3 0 7 18 20 16|, &lt;0 1 0 -2 -2 -1|]
{{Optimal ET sequence|legend=0| 12, 15, 27e }}
EDOs: 12f, 15, 27ef
Badness: 0.0208


===Ogene===
Badness (Sintel): 0.648
Commas: 56/55, 64/63, 91/90, 100/99


POTE generator: ~3/2 = 712.609
==== 13-limit ====
Subgroup: 2.3.5.7.11.13


Map: [&lt;3 0 7 18 20 -8|, &lt;0 1 0 -2 -2 4|]
Comma list: 40/39, 56/55, 64/63, 66/65
EDOs: 12, 15, 27e, 69bcef
Badness: 0.0229


===Agene===
Mapping: {{mapping| 3 0 7 18 20 16 | 0 1 0 -2 -2 -1 }}
Commas: 56/55, 64/63, 78/77, 100/99


POTE generator: ~3/2 = 709.677
Optimal tunings:  
* WE: ~5/4 = 398.0488{{c}}, ~3/2 = 708.5402{{c}} (~21/20 = 87.5574{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 712.6704{{c}} (~21/20 = 87.3296{{c}})


Map: [&lt;3 0 7 18 20 35|, &lt;0 1 0 -2 -2 -5|]
{{Optimal ET sequence|legend=0| 12f, 15, 27eff }}
EDOs: 12f, 27e
Badness: 0.0231


==Eugene==
Badness (Sintel): 0.859
Commas: 55/54, 64/63, 77/75


POTE generator: ~3/2 = 714.150
==== Ogene ====
Subgroup: 2.3.5.7.11.13


Map: [&lt;3 0 7 18 -4|, &lt;0 1 0 -2 3|]
Comma list: 56/55, 64/63, 91/90, 100/99
EDOs: 15, 27, 42
Badness: 0.0356


[[http://micro.soonlabel.com/gene_ward_smith/Others/Igs/Sad%20Like%20Winter%20Leaves.mp3|Sad Like Winter Leaves]] by [[http://soundcloud.com/cityoftheasleep/sad-like-winter-trees|Igliashon Jones]]
Mapping: {{mapping| 3 0 7 18 20 -8 | 0 1 0 -2 -2 4 }}
[[http://micro.soonlabel.com/gene_ward_smith/Others/Taylor/12of27sonatina.mp3|Galticeran Sonatina]] by [[http://soundcloud.com/joelgranttaylor/galticeran_sonatina|Joel Taylor]]


=Inflated=  
Optimal tunings:
Commas: 28/27, 128/125
* WE: ~5/4 = 398.6473{{c}}, ~3/2 = 710.1987{{c}} (~21/20 = 87.0959{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 712.5057{{c}} (~21/20 = 87.4943{{c}})


POTE generator: ~3/2 = 722.719
{{Optimal ET sequence|legend=0| 12, 15, 27e, 69bceef }}


Map: [&lt;3 0 7 -6|, &lt;0 1 0 3|]
Badness (Sintel): 0.946
Wedgie: &lt;&lt;3 0 9 -7 6 21||
EDOs: 15, 48bc, 63bc, 78bc
Badness: 0.0547


==11-limit==  
==== Agene ====
Commas: 28/27, 55/54, 128/125
Subgroup: 2.3.5.7.11.13


POTE generator: ~3/2 = 722.663
Comma list: 56/55, 64/63, 78/77, 100/99


Map: [&lt;3 0 7 -6|, &lt;0 1 0 3|]
Mapping: {{mapping| 3 0 7 18 20 35 | 0 1 0 -2 -2 -5 }}
EDOs: 15, 48bce, 63bce, 78bce
Badness: 0.0312


=Deflated=  
Optimal tunings:
Commas: 21/20, 128/125
* WE: ~5/4 = 398.5229{{c}}, ~3/2 = 707.0562{{c}} (~21/20 = 89.9897{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 710.1903{{c}} (~21/20 = 89.8097{{c}})


POTE generator: ~3/2 = 681.629
{{Optimal ET sequence|legend=0| 12f, 27e, 66cdeeef }}


Map: [&lt;3 0 7 13|, &lt;0 1 0 -1|]
Badness (Sintel): 0.955
Wedgie: &lt;&lt;3 0 -3 -7 -13 -7||
EDOs: 3, 9, 18bd, 21d, 30bd
Badness: 0.0591


=Hexe=  
=== Eugene ===
Commas: 50/49, 128/125
Subgroup: 2.3.5.7.11


[[POTE tuning|POTE generator]]: 710.963
Comma list: 55/54, 64/63, 77/75


Map: [&lt;6 0 14 17|, &lt;0 1 0 0|]
Mapping: {{mapping| 3 0 7 18 -4 | 0 1 0 -2 3 }}
Wedgie: &lt;&lt;6 0 0 -14 -17 0||
EDOs: [[6edo|6]], [[12edo|12]], [[30edo|30d]], [[[42edo|42d]], [[54edo|54cd]]
Badness: 0.0577


==11-limit==  
Optimal tunings:
Commas: 50/49, 56/55, 125/121
* WE: ~5/4 = 399.1743{{c}}, ~3/2 = 712.6763{{c}} (~21/20 = 85.6723{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 713.9414{{c}} (~21/20 = 86.0586{{c}})


POTE generator: ~3/2 = 714.304
{{Optimal ET sequence|legend=0| 12e, 15, 27, 42 }}


Map: [&lt;6 0 14 17 21|, &lt;0 1 0 0 0|]
Badness (Sintel): 1.18
EDOs: 6, 12, 30de
Badness: 0.0384


==13-limit==  
== August ==
Commas: 50/49, 56/55, 66/65, 105/104
August tempers out 36/35 and 225/224. It may be described as the {{nowrap| 9 & 12 }} temperament. Unlike augene, august calls for a flat tuning of the fifth, and besides [[12edo]], [[21edo]] is among the possible tunings.


POTE generator: ~3/2 = 710.005
[[Subgroup]]: 2.3.5.7


Map: [&lt;6 0 14 17 21 13|, &lt;0 1 0 0 0 1|]
[[Comma list]]: 36/35, 128/125
EDOs: 12f
Badness: 0.0359


=Hemiaug=
{{Mapping|legend=1| 3 0 7 -1 | 0 1 0 2 }}
Commas: 128/125, 245/243


[[POTE tuning|POTE generator]]: ~28/27 = 45.118
[[Optimal tuning]]s:
* [[WE]]: ~5/4 = 399.1036{{c}}, ~3/2 = 694.4509{{c}} (~16/15 = 103.7564{{c}})
: [[error map]]: {{val| -2.689 -10.193 +7.412 +15.594 }}
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 694.6812{{c}} (~16/15 = 105.3188{{c}})
: error map: {{val| 0.000 -7.274 +13.686 +20.537 }}


Map: [&lt;3 1 7 -1|, &lt;0 2 0 5|]
{{Optimal ET sequence|legend=1| 9, 12, 45cd }}
Wedgie: &lt;&lt;6 0 15 -14 7 35||
EDOs: [[24edo|24]], [[27edo|27]], [[105edo|105bc]]
Badness: 0.0705


==11-limit==
[[Badness]] (Sintel): 0.670
Commas: 56/55, 128/125, 245/243


POTE generator: ~28/27 = 45.788
=== 11-limit ===
Subgroup: 2.3.5.7.11


Map: [&lt;3 1 7 -1 1|, &lt;0 2 0 5 5|]
Comma list: 36/35, 45/44, 56/55
EDOs: 24, 27e, 51ce, 78ce
Badness: 0.0382


==13-limit==
Mapping: {{mapping| 3 0 7 -1 1 | 0 1 0 2 2 }}
Commas: 56/55, 91/90, 128/125, 245/243


POTE generator: ~28/27 = 46.250
Optimal tunings:  
* WE: ~5/4 = 398.9225{{c}}, ~3/2 = 690.6486{{c}} (~16/15 = 107.1966{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 690.8519{{c}} (~16/15 = 109.1481{{c}})


Map: [&lt;3 1 7 -1 1 13|, &lt;0 2 0 5 5 -1|]
{{Optimal ET sequence|legend=0| 9, 12, 21, 33e }}
EDOs: 24, 27e, 51ce, 78ce
Badness: 0.0302


=Triforce=
Badness (Sintel): 0.668
Commas: 49/48, 128/125


[[POTE tuning|POTE generator]]: ~7/6 = 247.049
==== 13-limit ====
Subgroup: 2.3.5.7.11.13


Map: [&lt;3 0 7 6|, &lt;0 2 0 1|]
Comma list: 27/26, 36/35, 45/44, 56/55
Wedgie: &lt;&lt;6 0 3 -14 -12 7||
EDOs: 6, 9, [[15edo|15]], [[24edo|24]], [[39edo|39]], [[63edo|63cd]], [[102edo|102cd]]
Badness: 0.0202


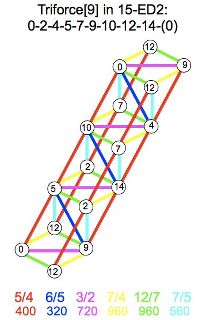
[[image:triforce9.jpg]]
Mapping: {{mapping| 3 0 7 -1 1 -3 | 0 1 0 2 2 3 }}


==11-limit==  
Optimal tunings:
Commas: 56/55, 77/75, 128/125
* WE: ~5/4 = 399.0956{{c}}, ~3/2 = 687.2261{{c}} (~16/15 = 110.9651{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 687.5057{{c}} (~16/15 = 112.4943{{c}})


[[POTE tuning|POTE generator]]: ~7/6 = 247.068
{{Optimal ET sequence|legend=0| 9, 12f, 21, 33ef }}


Map: [&lt;3 0 7 6 8|, &lt;0 2 0 1 1|]
Badness (Sintel): 0.762
EDOs: 6, 9, 15, 24, 39, [[63edo|63cd]], [[102edo|102cd]]
Badness: 0.0262


===Musical example:===  
==== Augustus ====
[[http://soundcloud.com/cityoftheasleep/the-triforce-of-courage15|The Triforce of Courage (tuned in 15edo)]] by Igliashon Jones
Subgroup: 2.3.5.7.11.13
==13-limit==
Commas: 49/48, 56/55, 66/65, 77/75


[[POTE tuning|POTE generator]]: ~7/6 = 248.313
Comma list: 26/25, 36/35, 45/44, 56/55


Map: [&lt;3 0 7 6 8 4|, &lt;0 2 0 1 1 3|]
Mapping: {{mapping| 3 0 7 -1 1 11 | 0 1 0 2 2 0 }}
EDOs: 6, 9, 15, 24, [[63edo|63cdf]], [[87edo|87cdf]]
Badness: 0.0202


[[triphi|Triforce(9) with L:s = phi]]
Optimal tunings:
* WE: ~5/4 = 400.4230{{c}}, ~3/2 = 686.0809{{c}} (~16/15 = 114.7650{{c}})
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 685.8446{{c}} (~16/15 = 114.1554{{c}})


==Semitriforce==
{{Optimal ET sequence|legend=0| 9, 12 }}
Commas: 49/48, 56/55, 77/75, 507/500


POTE generator: ~7/6 = 246.642
Badness (Sintel): 0.919


Map: [&lt;6 0 14 12 16 27|, &lt;0 2 0 1 1 -1|]
== Inflated ==
EDOs: 6, 24, 54cd, 78cd, 102cdf
[[Subgroup]]: 2.3.5.7
Badness: 0.0592


=== ===
[[Comma list]]: 28/27, 128/125
=Hemiug=
Commas: 128/125, 1323/1250


POTE generator: ~21/20 = 52.093
{{Mapping|legend=1| 3 0 7 -6 | 0 1 0 3 }}


Map: [&lt;3 1 7 14|, &lt;0 2 0 -3|]
[[Optimal tuning]]s:  
Wedgie: &lt;&lt;6 0 -9 -14 -31 -21||
* [[WE]]: ~5/4 = 398.4023{{c}}, ~3/2 = 719.8327{{c}} (~25/24 = 76.9719{{c}})
EDOs: 21, 24, 45c, 69cd
: [[error map]]: {{val| -3.762 +1.317 +4.909 +2.060 }}
Badness: 0.1378
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 721.0196{{c}} (~25/24 = 78.9804{{c}})
: error map: {{val| 0.000 +19.065 +13.686 -5.767 }}


==11-limit==
{{Optimal ET sequence|legend=1| 3d, 12d, 15 }}
Commas: 56/55, 128/125, 1323/1250


POTE generator: ~21/20 = 51.655
[[Badness]] (Sintel): 1.39


Map: [&lt;3 1 7 14 16|, &lt;0 2 0 -3 -3|]
=== 11-limit ===
EDOs: 21, 24, 69cd, 93cd
Subgroup: 2.3.5.7.11
Badness: 0.0681


==13-limit==
Comma list: 28/27, 55/54, 128/125
Commas: 56/55, 66/65, 105/104, 507/500


POTE generator: ~21/20 = 51.548
Mapping: {{mapping| 3 0 7 -6 -4 | 0 1 0 3 3 }}


Map: [&lt;3 1 7 14 16 13|, &lt;0 2 0 -3 -3 -1|]
Optimal tunings:  
EDOs: 21, 24, 69cdf, 93cdf
* WE: ~5/4 = 398.4016{{c}}, ~3/2 = 719.7758{{c}} (~25/24 = 77.0275{{c}})
Badness: 0.0423
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 720.9386{{c}} (~25/24 = 79.0614{{c}})


=Trug=
{{Optimal ET sequence|legend=0| 3de, 12de, 15 }}
Commas: 128/125, 360/343


POTE generator: ~48/35 = 501.980
Badness (Sintel): 1.03


Map: [&lt;3 1 7 6|, &lt;0 3 0 2|]
== Deflated ==
EDOs: 9bd, 12
[[Subgroup]]: 2.3.5.7
Badness: 0.1383


=Oodako=
[[Comma list]]: 21/20, 128/125
Commas: 128/125, 2401/2400


POTE generator: ~8/7 = 223.3540873874507317
{{Mapping|legend=1| 3 0 7 13 | 0 1 0 -1 }}


Map: [&lt;3 3 7 8|, &lt;0 4 0 1|]
[[Optimal tuning]]s:  
Wedgie: &lt;&lt;12 0 3 -28 -29 7||
* [[WE]]: ~5/4 = 401.9566{{c}}, ~3/2 = 684.9634{{c}} (~16/15 = 118.9497{{c}})
EDOs: 6, 21, 27, 75c, 102cd, 129bcd
: [[error map]]: {{val| +5.870 -11.122 +27.382 -34.224 }}
Badness: 0.1132
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~3/2 = 682.2587{{c}} (~16/15 = 117.7413{{c}})
: error map: {{val| 0.000 -19.696 +13.686 -51.085 }}


==11-limit==
{{Optimal ET sequence|legend=1| 3, 6b, 9 }}
Commas: 56/55, 128/125, 3773/3750


POTE generator: ~8/7 = 223.019
[[Badness]] (Sintel): 1.50


Map: [&lt;3 3 7 8 10|, &lt;0 4 0 1 1|]
=== 11-limit ===
EDOs: 6, 21, 27e
Subgroup: 2.3.5.7.11
Badness: 0.0592


==13-limit==
Comma list: 21/20, 33/32, 128/125
Commas: 56/55, 78/77, 128/125, 507/500


POTE generator: ~8/7 = 223.449
Mapping: {{mapping| 3 0 7 13 15 | 0 1 0 -1 -1 }}


Map: [&lt;3 3 7 8 10 12|, &lt;0 4 0 1 1 -2|]
Optimal tunings:  
EDOs: 6, 21, 27e
* WE: ~5/4 = 402.1799{{c}}, ~3/2 = 683.7477{{c}} (~16/15 = 120.6120{{c}})
Badness: 0.0423
* CWE: ~5/4 = 400.0000{{c}}, ~3/2 = 680.0162{{c}} (~16/15 = 119.9838{{c}})


=Hemisemiaug=
{{Optimal ET sequence|legend=0| 3, 6b, 9 }}
Commas: 128/125, 12005/11664


POTE generator: ~15/14 = 144.515
Badness (Sintel): 1.23


Map: [&lt;6 1 14 4|, &lt;0 2 0 3|]
== Hexe ==
Wedgie: &lt;&lt;12 0 18 -28 -5 42||
Hexe tempers out 50/49 and may be described as {{nowrap| 6 & 12 }}, viewed as [[6edo|6et]] with an independent generator for prime 3. Its ploidacot is hexaploid monocot.  
Edos: 18, 24, 42, 66c, 108bc
Badness: 0.2110


==11-limit==
[[Subgroup]]: 2.3.5.7
Commas: 56/55, 128/125, 3773/3645


POTE generator: ~15/14 = 144.780
[[Comma list]]: 50/49, 128/125


Map: [&lt;6 1 14 4 8|, &lt;0 2 0 3 3|]
{{Mapping|legend=1| 6 0 14 17 | 0 1 0 0 }}
EDOs: 24, 42e, 66ce, 108bce
Badness: 0.0807


=Niner=
: mapping generators: ~28/25, ~3
Niner gives 9 as the complexity of an otonal tetrad, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads.


Commas: 128/125, 686/675
[[Optimal tuning]]s:  
* [[WE]]: ~28/25 = 199.0488{{c}}, ~3/2 = 707.5815{{c}} (~25/24 = 88.6137{{c}})
: [[error map]]: {{val| +5.870 -11.122 +27.382 -34.224 }}
* [[CWE]]: ~28/25 = 200.0000{{c}}, ~3/2 = 708.6907{{c}} (~25/24 = 91.3093{{c}})
: error map: {{val| 0.000 +6.735 +13.686 +31.174 }}


POTE generator: ~3/2 = 707.167
{{Optimal ET sequence|legend=1| 6, 12, 30d, 42dd, 54cdd }}


Map: [&lt;9 0 21 11|, &lt;0 1 0 1|]
[[Badness]] (Sintel): 1.46
Wedgie: &lt;&lt;9 0 9 -21 -11 21||
EDOs: 9, 18, 27, 63c, 90c
Badness: 0.0672


==11-limit==  
=== 11-limit ===
Commas: 56/55, 128/125, 540/539
Subgroup: 2.3.5.7.11


POTE generator: ~3/2 = 706.726
Comma list: 50/49, 56/55, 125/121


Map: [&lt;9 0 21 11 17|, &lt;0 1 0 1 1|]
Mapping: {{mapping| 6 0 14 17 21 | 0 1 0 0 0 }}
EDOs: 9, 27e, 36, 63ce
Badness: 0.0349


==13-limit==  
Optimal tunings:
Commas: 56/55, 78/77, 91/90, 128/125
* WE: ~28/25 = 198.6942{{c}}, ~3/2 = 709.6404{{c}} (~25/24 = 85.1362{{c}})
* CWE: ~28/25 = 200.0000{{c}}, ~3/2 = 711.8043{{c}} (~25/24 = 88.1957{{c}})


POTE generator: ~3/2 = 706.889
{{Optimal ET sequence|legend=0| 6, 12, 30dee, 42ddeee }}


Map: [&lt;9 0 21 11 17 19|, &lt;0 1 0 1 1 1|]
Badness (Sintel): 1.27
EDOs: 9, 27e, 36, 63ce
Badness: 0.0241


==Music==  
=== 13-limit ===
[[https://www.prismnet.com/~hmiller/music/temp-augmented.html|Herman Miller's page about augmented temperament]]</pre></div>
Subgroup: 2.3.5.7.11.13
<h4>Original HTML content:</h4>
 
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;Augmented family&lt;/title&gt;&lt;/head&gt;&lt;body&gt;&lt;span style="display: block; text-align: right;"&gt;&lt;!-- ws:start:WikiTextTocRule:78:&amp;lt;img id=&amp;quot;wikitext@@toc@@normal&amp;quot; class=&amp;quot;WikiMedia WikiMediaToc&amp;quot; title=&amp;quot;Table of Contents&amp;quot; src=&amp;quot;/site/embedthumbnail/toc/normal?w=225&amp;amp;h=100&amp;quot;/&amp;gt; --&gt;&lt;div id="toc"&gt;&lt;h1 class="nopad"&gt;Table of Contents&lt;/h1&gt;&lt;!-- ws:end:WikiTextTocRule:78 --&gt;&lt;!-- ws:start:WikiTextTocRule:79: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Seven limit children"&gt;Seven limit children&lt;/a&gt;&lt;/div&gt;
Comma list: 50/49, 56/55, 66/65, 105/104
&lt;!-- ws:end:WikiTextTocRule:79 --&gt;&lt;!-- ws:start:WikiTextTocRule:80: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#August"&gt;August&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:80 --&gt;&lt;!-- ws:start:WikiTextTocRule:81: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#August-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
Mapping: {{mapping| 6 0 14 17 21 13 | 0 1 0 0 0 1 }}
&lt;!-- ws:end:WikiTextTocRule:81 --&gt;&lt;!-- ws:start:WikiTextTocRule:82: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#August-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:82 --&gt;&lt;!-- ws:start:WikiTextTocRule:83: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#August-Augustus"&gt;Augustus&lt;/a&gt;&lt;/div&gt;
Optimal tunings:
&lt;!-- ws:end:WikiTextTocRule:83 --&gt;&lt;!-- ws:start:WikiTextTocRule:84: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Augene"&gt;Augene&lt;/a&gt;&lt;/div&gt;
* WE: ~28/25 = 198.4492{{c}}, ~3/2 = 704.4994{{c}} (~25/24 = 89.2973{{c}})
&lt;!-- ws:end:WikiTextTocRule:84 --&gt;&lt;!-- ws:start:WikiTextTocRule:85: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Augene-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
* CWE: ~28/25 = 200.0000{{c}}, ~3/2 = 706.6050{{c}} (~16/15 = 93.3950{{c}})
&lt;!-- ws:end:WikiTextTocRule:85 --&gt;&lt;!-- ws:start:WikiTextTocRule:86: --&gt;&lt;div style="margin-left: 3em;"&gt;&lt;a href="#Augene-11-limit-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:86 --&gt;&lt;!-- ws:start:WikiTextTocRule:87: --&gt;&lt;div style="margin-left: 3em;"&gt;&lt;a href="#Augene-11-limit-Ogene"&gt;Ogene&lt;/a&gt;&lt;/div&gt;
{{Optimal ET sequence|legend=0| 6f, 12f }}
&lt;!-- ws:end:WikiTextTocRule:87 --&gt;&lt;!-- ws:start:WikiTextTocRule:88: --&gt;&lt;div style="margin-left: 3em;"&gt;&lt;a href="#Augene-11-limit-Agene"&gt;Agene&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:88 --&gt;&lt;!-- ws:start:WikiTextTocRule:89: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Augene-Eugene"&gt;Eugene&lt;/a&gt;&lt;/div&gt;
Badness (Sintel): 1.49
&lt;!-- ws:end:WikiTextTocRule:89 --&gt;&lt;!-- ws:start:WikiTextTocRule:90: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Inflated"&gt;Inflated&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:90 --&gt;&lt;!-- ws:start:WikiTextTocRule:91: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Inflated-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
== Triforce ==
&lt;!-- ws:end:WikiTextTocRule:91 --&gt;&lt;!-- ws:start:WikiTextTocRule:92: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Deflated"&gt;Deflated&lt;/a&gt;&lt;/div&gt;
[[File:triforce9.jpg|thumb|alt=triforce9.jpg|Lattice of triforce]]
&lt;!-- ws:end:WikiTextTocRule:92 --&gt;&lt;!-- ws:start:WikiTextTocRule:93: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Hexe"&gt;Hexe&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:93 --&gt;&lt;!-- ws:start:WikiTextTocRule:94: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hexe-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
Triforce tempers out 49/48 and may be described as {{nowrap| 9 & 15 }}. Its ploidacot is triploid alpha-dicot. [[24edo]] and [[39edo]] are among the possible tunings.
&lt;!-- ws:end:WikiTextTocRule:94 --&gt;&lt;!-- ws:start:WikiTextTocRule:95: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hexe-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:95 --&gt;&lt;!-- ws:start:WikiTextTocRule:96: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Hemiaug"&gt;Hemiaug&lt;/a&gt;&lt;/div&gt;
[[Subgroup]]: 2.3.5.7
&lt;!-- ws:end:WikiTextTocRule:96 --&gt;&lt;!-- ws:start:WikiTextTocRule:97: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hemiaug-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:97 --&gt;&lt;!-- ws:start:WikiTextTocRule:98: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hemiaug-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
[[Comma list]]: 49/48, 128/125
&lt;!-- ws:end:WikiTextTocRule:98 --&gt;&lt;!-- ws:start:WikiTextTocRule:99: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Triforce"&gt;Triforce&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:99 --&gt;&lt;!-- ws:start:WikiTextTocRule:100: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Triforce-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
{{Mapping|legend=1| 3 0 7 6 | 0 2 0 1 }}
&lt;!-- ws:end:WikiTextTocRule:100 --&gt;&lt;!-- ws:start:WikiTextTocRule:101: --&gt;&lt;div style="margin-left: 3em;"&gt;&lt;a href="#Triforce-11-limit-Musical example:"&gt;Musical example:&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:101 --&gt;&lt;!-- ws:start:WikiTextTocRule:102: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Triforce-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
: mapping generators: ~5/4, ~7/4
&lt;!-- ws:end:WikiTextTocRule:102 --&gt;&lt;!-- ws:start:WikiTextTocRule:103: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Triforce-Semitriforce"&gt;Semitriforce&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:103 --&gt;&lt;!-- ws:start:WikiTextTocRule:104: --&gt;&lt;div style="margin-left: 3em;"&gt;&lt;a href="#toc25"&gt; &lt;/a&gt;&lt;/div&gt;
[[Optimal tuning]]s:  
&lt;!-- ws:end:WikiTextTocRule:104 --&gt;&lt;!-- ws:start:WikiTextTocRule:105: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Hemiug"&gt;Hemiug&lt;/a&gt;&lt;/div&gt;
* [[WE]]: ~5/4 = 399.7480{{c}}, ~7/4 = 952.3507{{c}} (~35/32 = 152.8547{{c}})
&lt;!-- ws:end:WikiTextTocRule:105 --&gt;&lt;!-- ws:start:WikiTextTocRule:106: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hemiug-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
: [[error map]]: {{val| -0.756 +2.746 +11.922 -17.987 }}
&lt;!-- ws:end:WikiTextTocRule:106 --&gt;&lt;!-- ws:start:WikiTextTocRule:107: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hemiug-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~7/4 = 952.7463{{c}} (~35/32 = 152.7463{{c}})
&lt;!-- ws:end:WikiTextTocRule:107 --&gt;&lt;!-- ws:start:WikiTextTocRule:108: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Trug"&gt;Trug&lt;/a&gt;&lt;/div&gt;
: error map: {{val| 0.000 +3.538 +13.686 -16.080 }}
&lt;!-- ws:end:WikiTextTocRule:108 --&gt;&lt;!-- ws:start:WikiTextTocRule:109: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Oodako"&gt;Oodako&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:109 --&gt;&lt;!-- ws:start:WikiTextTocRule:110: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Oodako-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
{{Optimal ET sequence|legend=1| 6, 9, 15, 24, 39 }}
&lt;!-- ws:end:WikiTextTocRule:110 --&gt;&lt;!-- ws:start:WikiTextTocRule:111: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Oodako-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:111 --&gt;&lt;!-- ws:start:WikiTextTocRule:112: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Hemisemiaug"&gt;Hemisemiaug&lt;/a&gt;&lt;/div&gt;
[[Badness]] (Sintel): 1.39
&lt;!-- ws:end:WikiTextTocRule:112 --&gt;&lt;!-- ws:start:WikiTextTocRule:113: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Hemisemiaug-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:113 --&gt;&lt;!-- ws:start:WikiTextTocRule:114: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Niner"&gt;Niner&lt;/a&gt;&lt;/div&gt;
=== 11-limit ===
&lt;!-- ws:end:WikiTextTocRule:114 --&gt;&lt;!-- ws:start:WikiTextTocRule:115: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Niner-11-limit"&gt;11-limit&lt;/a&gt;&lt;/div&gt;
Subgroup: 2.3.5.7.11
&lt;!-- ws:end:WikiTextTocRule:115 --&gt;&lt;!-- ws:start:WikiTextTocRule:116: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Niner-13-limit"&gt;13-limit&lt;/a&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:116 --&gt;&lt;!-- ws:start:WikiTextTocRule:117: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Niner-Music"&gt;Music&lt;/a&gt;&lt;/div&gt;
Comma list: 49/48, 56/55, 77/75
&lt;!-- ws:end:WikiTextTocRule:117 --&gt;&lt;!-- ws:start:WikiTextTocRule:118: --&gt;&lt;/div&gt;
 
&lt;!-- ws:end:WikiTextTocRule:118 --&gt;&lt;br /&gt;
Mapping: {{mapping| 3 0 7 6 8 | 0 2 0 1 1 }}
&lt;a class="wiki_link" href="http://xenharmonie.wikispaces.com/%C3%BCberm%C3%A4ssige%20Temperaturen"&gt;Deutsch&lt;/a&gt;&lt;br /&gt;
 
&lt;/span&gt;&lt;br /&gt;
Optimal tunings:  
The 5-limit parent comma for the &lt;strong&gt;augmented family&lt;/strong&gt; is 128/125, the &lt;a class="wiki_link" href="/128_125"&gt;diesis&lt;/a&gt;. Its &lt;a class="wiki_link" href="/monzo"&gt;monzo&lt;/a&gt; is |7 0 -3&amp;gt;, and flipping that yields &amp;lt;&amp;lt;3 0 -7|| for the &lt;a class="wiki_link" href="/wedgie"&gt;wedgie&lt;/a&gt;. Hence the period is 1/3 octave, and this is what is used for a major third. The &lt;a class="wiki_link" href="/generator"&gt;generator&lt;/a&gt; can be taken as a fifth or a semitone, and &lt;a class="wiki_link" href="/12edo"&gt;12edo&lt;/a&gt;, with its excellent fifth, is an obvious tuning for &lt;a class="wiki_link" href="/5-limit"&gt;5-limit&lt;/a&gt; augmented, though a sharper fifth might be preferred to go with the sharp third.&lt;br /&gt;
* WE: ~5/4 = 399.7654{{c}}, ~7/4 = 952.3730{{c}} (~12/11 = 152.8421{{c}})
&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~7/4 = 952.7447{{c}} (~12/11 = 152.7447{{c}})
&lt;!-- ws:start:WikiTextHeadingRule:0:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc0"&gt;&lt;a name="Seven limit children"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:0 --&gt;Seven limit children&lt;/h1&gt;
 
The second comma of the &lt;a class="wiki_link" href="/Normal%20lists"&gt;normal comma list&lt;/a&gt; defines which &lt;a class="wiki_link" href="/7-limit"&gt;7-limit&lt;/a&gt; family member we are looking at. August adds 36/35, augene 64/63, hexe 256/245, hemiaug 245/243, and hemis 49/48. Hexe splits the period to 1/6 octave, and hemiaug the generator, giving quarter-tones instead of semitones.&lt;br /&gt;
{{Optimal ET sequence|legend=0| 6, 9, 15, 24, 39 }}
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:2:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc1"&gt;&lt;a name="August"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:2 --&gt;August&lt;/h1&gt;
Badness (Sintel): 0.865
&lt;a class="wiki_link" href="/Comma"&gt;Comma&lt;/a&gt;s: 36/35, 128/125&lt;br /&gt;
 
&lt;br /&gt;
; Music
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: 696.011&lt;br /&gt;
* [https://cityoftheasleep.bandcamp.com/track/the-triforce-of-courage-24edo ''The Triforce of Courage (24edo)'']{{dead link}} by [[Igliashon Jones]] (2018)
&lt;br /&gt;
* [https://www.chrisvaisvil.com/2-2-1-2-2-1-2-2-1-mode-of-15-edo/ ''2-2-1-2-2-1-2-2-1 mode of 15 edo''] [https://web.archive.org/web/20201127015017/http://micro.soonlabel.com/15-ET/20130831_221of15.mp3 play] by [[Chris Vaisvil]] (2013)
&lt;a class="wiki_link" href="/Map"&gt;Map&lt;/a&gt;: [&amp;lt;3 0 7 -1|, &amp;lt;0 1 0 2|]&lt;br /&gt;
 
&lt;a class="wiki_link" href="/Wedgie"&gt;Wedgie&lt;/a&gt;: &amp;lt;&amp;lt;3 0 6 -7 1 14||&lt;br /&gt;
==== 13-limit ====
&lt;a class="wiki_link" href="/edo"&gt;EDOs&lt;/a&gt;: &lt;a class="wiki_link" href="/9edo"&gt;9&lt;/a&gt;, &lt;a class="wiki_link" href="/12edo"&gt;12&lt;/a&gt;, &lt;a class="wiki_link" href="/45edo"&gt;45cd&lt;/a&gt;, &lt;a class="wiki_link" href="/57edo"&gt;57cd&lt;/a&gt;, &lt;a class="wiki_link" href="/69edo"&gt;69cd&lt;/a&gt;&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
&lt;a class="wiki_link" href="/Badness"&gt;Badness&lt;/a&gt;: 0.0265&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 49/48, 56/55, 66/65, 77/75
&lt;!-- ws:start:WikiTextHeadingRule:4:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc2"&gt;&lt;a name="August-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:4 --&gt;11-limit&lt;/h2&gt;
 
Commas: 36/35, 45/44, 56/55&lt;br /&gt;
Mapping: {{mapping| 3 0 7 6 8 4 | 0 2 0 1 1 3 }}
&lt;br /&gt;
 
POTE generator: ~3/2 = 692.514&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~5/4 = 399.7107{{c}}, ~7/4 = 950.9983{{c}} (~12/11 = 151.5768{{c}})
Map: [&amp;lt;3 0 7 -1 1|, &amp;lt;0 1 0 2 2|]&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~7/4 = 951.4465{{c}} (~12/11 = 151.4465{{c}})
EDOs: 9, 12, &lt;a class="wiki_link" href="/21edo"&gt;21&lt;/a&gt;, &lt;a class="wiki_link" href="/33edo"&gt;33e&lt;/a&gt;, &lt;a class="wiki_link" href="/45edo"&gt;45cde&lt;/a&gt;&lt;br /&gt;
 
Badness: 0.0202&lt;br /&gt;
{{Optimal ET sequence|legend=0| 6f, 9, 15, 24 }}
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:6:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc3"&gt;&lt;a name="August-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:6 --&gt;13-limit&lt;/h2&gt;
Badness (Sintel): 0.837
Commas: 27/26, 36/35, 45/44, 56/55&lt;br /&gt;
 
&lt;br /&gt;
; Scales
POTE generator: ~3/2 = 688.783&lt;br /&gt;
* [[triphi]], Triforce[9] with L:s = phi
&lt;br /&gt;
 
Map: [&amp;lt;3 0 7 -1 1 -3|, &amp;lt;0 1 0 2 2 3|]&lt;br /&gt;
==== Semitriforce ====
EDOs: 9, 12, &lt;a class="wiki_link" href="/21edo"&gt;21&lt;/a&gt;, &lt;a class="wiki_link" href="/33edo"&gt;33ef&lt;/a&gt;, &lt;a class="wiki_link" href="/54edo"&gt;54bcef&lt;/a&gt;&lt;br /&gt;
This extension splits the period into 1/6-octave for ~44/39. Its ploidacot is hexaploid dicot.
Badness: 0.0184&lt;br /&gt;
 
&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
&lt;!-- ws:start:WikiTextHeadingRule:8:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc4"&gt;&lt;a name="August-Augustus"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:8 --&gt;Augustus&lt;/h2&gt;
 
Commas: 26/25, 36/35, 45/44, 56/55&lt;br /&gt;
Comma list: 49/48, 56/55, 77/75, 507/500
&lt;br /&gt;
 
POTE generator: ~3/2 = 685.356&lt;br /&gt;
Mapping: {{mapping| 6 0 14 12 16 27 | 0 2 0 1 1 -1 }}
&lt;br /&gt;
 
Map: [&amp;lt;3 0 7 -1 1 11|, &amp;lt;0 1 0 2 2 0|]&lt;br /&gt;
: mapping generators: ~44/39, ~7/4
EDOs: 9, 12, 21f&lt;br /&gt;
 
Badness: 0.0222&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~44/39 = 199.8321{{c}}, ~7/4 = 952.5580{{c}} (~40/39 = 46.6024{{c}})
&lt;!-- ws:start:WikiTextHeadingRule:10:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc5"&gt;&lt;a name="Augene"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:10 --&gt;Augene&lt;/h1&gt;
* CWE: ~44/39 = 200.0000{{c}}, ~7/4 = 953.2005{{c}} (~40/39 = 46.7995{{c}})
Commas: 64/63, 126/125&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=0| 6, 18bd, 24 }}
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: 709.257&lt;br /&gt;
 
&lt;br /&gt;
Badness (Sintel): 2.44
Map: [&amp;lt;3 0 7 18|, &amp;lt;0 1 0 -2|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;3 0 -6 -7 -18 -14||&lt;br /&gt;
== Hemiaug ==
EDOs: &lt;a class="wiki_link" href="/12edo"&gt;12&lt;/a&gt;, &lt;a class="wiki_link" href="/27edo"&gt;27&lt;/a&gt;, &lt;a class="wiki_link" href="/39edo"&gt;39d&lt;/a&gt;, &lt;a class="wiki_link" href="/66edo"&gt;66cd&lt;/a&gt;&lt;br /&gt;
Hemiaug tempers out 245/243 and may be described as {{nowrap| 24 & 27 }}. The generator may be taken as ~14/9, but also a neutral third or a neutral second that stand in for 11/9~16/13 and 12/11~13/12 in the higher limits, respectively. Hemiaug's ploidacot is triploid dicot. [[27edo]] makes for a recommendable tuning in the 7-limit, but [[51edo]] serves better in the higher limits.
Badness: 0.0248&lt;br /&gt;
 
&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
&lt;!-- ws:start:WikiTextHeadingRule:12:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc6"&gt;&lt;a name="Augene-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:12 --&gt;11-limit&lt;/h2&gt;
 
Commas: 56/55, 64/63, 100/99&lt;br /&gt;
[[Comma list]]: 128/125, 245/243
&lt;br /&gt;
 
POTE generator: ~3/2 = 711.177&lt;br /&gt;
{{Mapping|legend=1| 3 1 7 -1 | 0 2 0 5 }}
&lt;br /&gt;
 
Map: [&amp;lt;3 0 7 18 20|, &amp;lt;0 1 0 -2 -2|]&lt;br /&gt;
: mapping generators: ~5/4, ~14/9
EDOs: 12, 15, 27e&lt;br /&gt;
 
Badness: 0.0196&lt;br /&gt;
[[Optimal tuning]]s:  
&lt;br /&gt;
* [[WE]]: ~5/4 = 398.9278{{c}}, ~14/9 = 752.8583{{c}} (~36/35 = 44.9973{{c}})
&lt;!-- ws:start:WikiTextHeadingRule:14:&amp;lt;h3&amp;gt; --&gt;&lt;h3 id="toc7"&gt;&lt;a name="Augene-11-limit-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:14 --&gt;13-limit&lt;/h3&gt;
: [[error map]]: {{val| -3.217 +2.689 +6.181 -3.462 }}
Commas: 40/39, 56/55, 64/63, 66/65&lt;br /&gt;
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~14/9 = 754.2078{{c}} (~36/35 = 45.7922{{c}})
&lt;br /&gt;
: error map: {{val| 0.000 +6.461 +13.686 +2.213 }}
POTE generator: ~3/2 = 712.013&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=1| 24, 27 }}
Map: [&amp;lt;3 0 7 18 20 16|, &amp;lt;0 1 0 -2 -2 -1|]&lt;br /&gt;
 
EDOs: 12f, 15, 27ef&lt;br /&gt;
[[Badness]] (Sintel): 1.78
Badness: 0.0208&lt;br /&gt;
 
&lt;br /&gt;
=== 11-limit ===
&lt;!-- ws:start:WikiTextHeadingRule:16:&amp;lt;h3&amp;gt; --&gt;&lt;h3 id="toc8"&gt;&lt;a name="Augene-11-limit-Ogene"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:16 --&gt;Ogene&lt;/h3&gt;
Subgroup: 2.3.5.7.11
Commas: 56/55, 64/63, 91/90, 100/99&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 128/125, 243/242
POTE generator: ~3/2 = 712.609&lt;br /&gt;
 
&lt;br /&gt;
Mapping: {{mapping| 3 1 7 -1 1 | 0 2 0 5 5 }}
Map: [&amp;lt;3 0 7 18 20 -8|, &amp;lt;0 1 0 -2 -2 4|]&lt;br /&gt;
 
EDOs: 12, 15, 27e, 69bcef&lt;br /&gt;
Optimal tunings:  
Badness: 0.0229&lt;br /&gt;
* WE: ~5/4 = 398.8946{{c}}, ~14/9 = 752.1272{{c}} (~36/35 = 45.6619{{c}})
&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~14/9 = 753.5000{{c}} (~36/35 = 46.5000{{c}})
&lt;!-- ws:start:WikiTextHeadingRule:18:&amp;lt;h3&amp;gt; --&gt;&lt;h3 id="toc9"&gt;&lt;a name="Augene-11-limit-Agene"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:18 --&gt;Agene&lt;/h3&gt;
 
Commas: 56/55, 64/63, 78/77, 100/99&lt;br /&gt;
{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}
&lt;br /&gt;
 
POTE generator: ~3/2 = 709.677&lt;br /&gt;
Badness (Sintel): 1.26
&lt;br /&gt;
 
Map: [&amp;lt;3 0 7 18 20 35|, &amp;lt;0 1 0 -2 -2 -5|]&lt;br /&gt;
=== 13-limit ===
EDOs: 12f, 27e&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
Badness: 0.0231&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 91/90, 128/125, 243/242
&lt;!-- ws:start:WikiTextHeadingRule:20:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc10"&gt;&lt;a name="Augene-Eugene"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:20 --&gt;Eugene&lt;/h2&gt;
 
Commas: 55/54, 64/63, 77/75&lt;br /&gt;
Mapping: {{mapping| 3 1 7 -1 1 13 | 0 2 0 5 5 -1 }}
&lt;br /&gt;
 
POTE generator: ~3/2 = 714.150&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~5/4 = 399.1053{{c}}, ~14/9 = 752.0643{{c}} (~36/35 = 46.1463{{c}})
Map: [&amp;lt;3 0 7 18 -4|, &amp;lt;0 1 0 -2 3|]&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~14/9 = 753.3806{{c}} (~36/35 = 46.6194{{c}})
EDOs: 15, 27, 42&lt;br /&gt;
 
Badness: 0.0356&lt;br /&gt;
{{Optimal ET sequence|legend=0| 24, 27e, 51ce }}
&lt;br /&gt;
 
&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Igs/Sad%20Like%20Winter%20Leaves.mp3" rel="nofollow"&gt;Sad Like Winter Leaves&lt;/a&gt; by &lt;a class="wiki_link_ext" href="http://soundcloud.com/cityoftheasleep/sad-like-winter-trees" rel="nofollow"&gt;Igliashon Jones&lt;/a&gt;&lt;br /&gt;
Badness (Sintel): 1.25
&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Taylor/12of27sonatina.mp3" rel="nofollow"&gt;Galticeran Sonatina&lt;/a&gt; by &lt;a class="wiki_link_ext" href="http://soundcloud.com/joelgranttaylor/galticeran_sonatina" rel="nofollow"&gt;Joel Taylor&lt;/a&gt;&lt;br /&gt;
 
&lt;br /&gt;
== Hemiug ==
&lt;!-- ws:start:WikiTextHeadingRule:22:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc11"&gt;&lt;a name="Inflated"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:22 --&gt;Inflated&lt;/h1&gt;
Hemiug tempers out 1323/1250 and may be described as {{nowrap| 21 & 24 }}. The generator is a similar interval but for ~32/21 instead of ~14/9, and the ploidacot is triploid dicot, the same as hemiaug.
Commas: 28/27, 128/125&lt;br /&gt;
 
&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
POTE generator: ~3/2 = 722.719&lt;br /&gt;
 
&lt;br /&gt;
[[Comma list]]: 128/125, 1323/1250
Map: [&amp;lt;3 0 7 -6|, &amp;lt;0 1 0 3|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;3 0 9 -7 6 21||&lt;br /&gt;
{{Mapping|legend=1| 3 1 7 14 | 0 2 0 -3 }}
EDOs: 15, 48bc, 63bc, 78bc&lt;br /&gt;
 
Badness: 0.0547&lt;br /&gt;
: mapping generators: ~5/4, ~32/21
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:24:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc12"&gt;&lt;a name="Inflated-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:24 --&gt;11-limit&lt;/h2&gt;
[[Optimal tuning]]s:  
Commas: 28/27, 55/54, 128/125&lt;br /&gt;
* [[WE]]: ~5/4 = 400.1805{{c}}, ~32/21 = 748.2436{{c}} (~21/20 = 52.1174{{c}})
&lt;br /&gt;
: [[error map]]: {{val| +0.542 -5.287 +14.950 -11.030 }}
POTE generator: ~3/2 = 722.663&lt;br /&gt;
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~32/21 = 747.9138{{c}} (~21/20 = 52.0862{{c}})
&lt;br /&gt;
: error map: {{val| 0.000 -6.127 +13.686 -12.567 }}
Map: [&amp;lt;3 0 7 -6|, &amp;lt;0 1 0 3|]&lt;br /&gt;
 
EDOs: 15, 48bce, 63bce, 78bce&lt;br /&gt;
{{Optimal ET sequence|legend=1| 21, 24, 45c }}
Badness: 0.0312&lt;br /&gt;
 
&lt;br /&gt;
[[Badness]] (Sintel): 3.49
&lt;!-- ws:start:WikiTextHeadingRule:26:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc13"&gt;&lt;a name="Deflated"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:26 --&gt;Deflated&lt;/h1&gt;
 
Commas: 21/20, 128/125&lt;br /&gt;
=== 11-limit ===
&lt;br /&gt;
Subgroup: 2.3.5.7.11
POTE generator: ~3/2 = 681.629&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 128/125, 1323/1250
Map: [&amp;lt;3 0 7 13|, &amp;lt;0 1 0 -1|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;3 0 -3 -7 -13 -7||&lt;br /&gt;
Mapping: {{mapping| 3 1 7 14 16 | 0 2 0 -3 -3 }}
EDOs: 3, 9, 18bd, 21d, 30bd&lt;br /&gt;
 
Badness: 0.0591&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~5/4 = 400.0637{{c}}, ~32/21 = 748.4638{{c}} (~33/32 = 51.6637{{c}})
&lt;!-- ws:start:WikiTextHeadingRule:28:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc14"&gt;&lt;a name="Hexe"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:28 --&gt;Hexe&lt;/h1&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~32/21 = 748.3383{{c}} (~33/32 = 51.6617{{c}})
Commas: 50/49, 128/125&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=0| 21, 24 }}
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: 710.963&lt;br /&gt;
 
&lt;br /&gt;
Badness (Sintel): 2.25
Map: [&amp;lt;6 0 14 17|, &amp;lt;0 1 0 0|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;6 0 0 -14 -17 0||&lt;br /&gt;
=== 13-limit ===
EDOs: &lt;a class="wiki_link" href="/6edo"&gt;6&lt;/a&gt;, &lt;a class="wiki_link" href="/12edo"&gt;12&lt;/a&gt;, &lt;a class="wiki_link" href="/30edo"&gt;30d&lt;/a&gt;, [&lt;a class="wiki_link" href="/42edo"&gt;42d&lt;/a&gt;, &lt;a class="wiki_link" href="/54edo"&gt;54cd&lt;/a&gt;&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
Badness: 0.0577&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 66/65, 105/104, 507/500
&lt;!-- ws:start:WikiTextHeadingRule:30:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc15"&gt;&lt;a name="Hexe-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:30 --&gt;11-limit&lt;/h2&gt;
 
Commas: 50/49, 56/55, 125/121&lt;br /&gt;
Mapping: {{mapping| 3 1 7 14 16 13 | 0 2 0 -3 -3 -1 }}
&lt;br /&gt;
 
POTE generator: ~3/2 = 714.304&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~5/4 = 399.8855{{c}}, ~32/21 = 748.2378{{c}} (~33/32 = 51.5332{{c}})
Map: [&amp;lt;6 0 14 17 21|, &amp;lt;0 1 0 0 0|]&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~32/21 = 748.4655{{c}} (~33/32 = 51.5345{{c}})
EDOs: 6, 12, 30de&lt;br /&gt;
 
Badness: 0.0384&lt;br /&gt;
{{Optimal ET sequence|legend=0| 21, 24 }}
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:32:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc16"&gt;&lt;a name="Hexe-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:32 --&gt;13-limit&lt;/h2&gt;
Badness (Sintel): 1.75
Commas: 50/49, 56/55, 66/65, 105/104&lt;br /&gt;
 
&lt;br /&gt;
== Oodako ==
POTE generator: ~3/2 = 710.005&lt;br /&gt;
Oodako tempers out 2401/2400 and may be described as {{nowrap| 21 & 27 }}. It is generated by a quarter of a fifth, which stands in for ~28/25. Its ploidacot is triploid tetracot.
&lt;br /&gt;
 
Map: [&amp;lt;6 0 14 17 21 13|, &amp;lt;0 1 0 0 0 1|]&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
EDOs: 12f&lt;br /&gt;
 
Badness: 0.0359&lt;br /&gt;
[[Comma list]]: 128/125, 2401/2400
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:34:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc17"&gt;&lt;a name="Hemiaug"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:34 --&gt;Hemiaug&lt;/h1&gt;
{{Mapping|legend=1| 3 3 7 8 | 0 4 0 1 }}
Commas: 128/125, 245/243&lt;br /&gt;
 
&lt;br /&gt;
: mapping generators: ~5/4, ~28/25
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: ~28/27 = 45.118&lt;br /&gt;
 
&lt;br /&gt;
[[Optimal tuning]]s:  
Map: [&amp;lt;3 1 7 -1|, &amp;lt;0 2 0 5|]&lt;br /&gt;
* [[WE]]: ~5/4 = 399.0296{{c}}, ~28/25 = 176.2174{{c}} (~49/48 = 46.5949{{c}})
Wedgie: &amp;lt;&amp;lt;6 0 15 -14 7 35||&lt;br /&gt;
: [[error map]]: {{val| -2.911 +0.004 +6.894 -0.371 }}
EDOs: &lt;a class="wiki_link" href="/24edo"&gt;24&lt;/a&gt;, &lt;a class="wiki_link" href="/27edo"&gt;27&lt;/a&gt;, &lt;a class="wiki_link" href="/105edo"&gt;105bc&lt;/a&gt;&lt;br /&gt;
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~28/25 = 176.2984{{c}} (~49/48 = 47.4031{{c}})
Badness: 0.0705&lt;br /&gt;
: error map: {{val| 0.000 +3.239 +13.686 +7.473 }}
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:36:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc18"&gt;&lt;a name="Hemiaug-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:36 --&gt;11-limit&lt;/h2&gt;
{{Optimal ET sequence|legend=1| 6, 21, 27, 75c, 102ccd, 129bccd }}
Commas: 56/55, 128/125, 245/243&lt;br /&gt;
 
&lt;br /&gt;
[[Badness]] (Sintel): 2.86
POTE generator: ~28/27 = 45.788&lt;br /&gt;
 
&lt;br /&gt;
=== 11-limit ===
Map: [&amp;lt;3 1 7 -1 1|, &amp;lt;0 2 0 5 5|]&lt;br /&gt;
Subgroup: 2.3.5.7.11
EDOs: 24, 27e, 51ce, 78ce&lt;br /&gt;
 
Badness: 0.0382&lt;br /&gt;
Comma list: 56/55, 128/125, 2401/2400
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:38:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc19"&gt;&lt;a name="Hemiaug-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:38 --&gt;13-limit&lt;/h2&gt;
Mapping: {{mapping| 3 3 7 8 10 | 0 4 0 1 1 }}
Commas: 56/55, 91/90, 128/125, 245/243&lt;br /&gt;
 
&lt;br /&gt;
Optimal tunings:  
POTE generator: ~28/27 = 46.250&lt;br /&gt;
* WE: ~5/4 = 398.6615{{c}}, ~11/10 = 176.3886{{c}} (~49/48 = 45.8843{{c}})
&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~11/10 = 176.5471{{c}} (~49/48 = 46.9059{{c}})
Map: [&amp;lt;3 1 7 -1 1 13|, &amp;lt;0 2 0 5 5 -1|]&lt;br /&gt;
 
EDOs: 24, 27e, 51ce, 78ce&lt;br /&gt;
{{Optimal ET sequence|legend=0| 6, 21, 27e }}
Badness: 0.0302&lt;br /&gt;
 
&lt;br /&gt;
Badness (Sintel): 1.96
&lt;!-- ws:start:WikiTextHeadingRule:40:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc20"&gt;&lt;a name="Triforce"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:40 --&gt;Triforce&lt;/h1&gt;
 
Commas: 49/48, 128/125&lt;br /&gt;
=== 13-limit ===
&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: ~7/6 = 247.049&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 78/77, 128/125, 507/500
Map: [&amp;lt;3 0 7 6|, &amp;lt;0 2 0 1|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;6 0 3 -14 -12 7||&lt;br /&gt;
Mapping: {{mapping| 3 3 7 8 10 12 | 0 4 0 1 1 -2 }}
EDOs: 6, 9, &lt;a class="wiki_link" href="/15edo"&gt;15&lt;/a&gt;, &lt;a class="wiki_link" href="/24edo"&gt;24&lt;/a&gt;, &lt;a class="wiki_link" href="/39edo"&gt;39&lt;/a&gt;, &lt;a class="wiki_link" href="/63edo"&gt;63cd&lt;/a&gt;, &lt;a class="wiki_link" href="/102edo"&gt;102cd&lt;/a&gt;&lt;br /&gt;
 
Badness: 0.0202&lt;br /&gt;
Optimal tunings:  
&lt;br /&gt;
* WE: ~5/4 = 398.8612{{c}}, ~11/10 = 176.0486{{c}} (~49/48 = 46.7640{{c}})
&lt;!-- ws:start:WikiTextLocalImageRule:119:&amp;lt;img src=&amp;quot;/file/view/triforce9.jpg/271381934/triforce9.jpg&amp;quot; alt=&amp;quot;&amp;quot; title=&amp;quot;&amp;quot; /&amp;gt; --&gt;&lt;img src="/file/view/triforce9.jpg/271381934/triforce9.jpg" alt="triforce9.jpg" title="triforce9.jpg" /&gt;&lt;!-- ws:end:WikiTextLocalImageRule:119 --&gt;&lt;br /&gt;
* CWE: ~5/4 = 400.0000{{c}}, ~11/10 = 176.3326{{c}} (~49/48 = 47.3348{{c}})
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:42:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc21"&gt;&lt;a name="Triforce-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:42 --&gt;11-limit&lt;/h2&gt;
{{Optimal ET sequence|legend=0| 6, 21, 27e }}
Commas: 56/55, 77/75, 128/125&lt;br /&gt;
 
&lt;br /&gt;
Badness (Sintel): 1.75
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: ~7/6 = 247.068&lt;br /&gt;
 
&lt;br /&gt;
== Hemisemiaug ==
Map: [&amp;lt;3 0 7 6 8|, &amp;lt;0 2 0 1 1|]&lt;br /&gt;
Hemisemiaug tempers out 12005/11664 and splits both the period and generator of augmented in two. Its ploidacot is hexaploid alpha-dicot.
EDOs: 6, 9, 15, 24, 39, &lt;a class="wiki_link" href="/63edo"&gt;63cd&lt;/a&gt;, &lt;a class="wiki_link" href="/102edo"&gt;102cd&lt;/a&gt;&lt;br /&gt;
 
Badness: 0.0262&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:44:&amp;lt;h3&amp;gt; --&gt;&lt;h3 id="toc22"&gt;&lt;a name="Triforce-11-limit-Musical example:"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:44 --&gt;Musical example:&lt;/h3&gt;
[[Comma list]]: 128/125, 12005/11664
&lt;a class="wiki_link_ext" href="http://soundcloud.com/cityoftheasleep/the-triforce-of-courage15" rel="nofollow"&gt;The Triforce of Courage (tuned in 15edo)&lt;/a&gt; by Igliashon Jones&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:46:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc23"&gt;&lt;a name="Triforce-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:46 --&gt;13-limit&lt;/h2&gt;
{{Mapping|legend=1| 6 1 14 4 | 0 2 0 3 }}
Commas: 49/48, 56/55, 66/65, 77/75&lt;br /&gt;
 
&lt;br /&gt;
: mapping generators: ~54/49, ~45/28
&lt;a class="wiki_link" href="/POTE%20tuning"&gt;POTE generator&lt;/a&gt;: ~7/6 = 248.313&lt;br /&gt;
 
&lt;br /&gt;
[[Optimal tuning]]s:  
Map: [&amp;lt;3 0 7 6 8 4|, &amp;lt;0 2 0 1 1 3|]&lt;br /&gt;
* [[WE]]: ~54/49 = 199.5469{{c}}, ~45/28 = 853.5468{{c}} (~36/35 = 55.3594{{c}})
EDOs: 6, 9, 15, 24, &lt;a class="wiki_link" href="/63edo"&gt;63cdf&lt;/a&gt;, &lt;a class="wiki_link" href="/87edo"&gt;87cdf&lt;/a&gt;&lt;br /&gt;
: [[error map]]: {{val| -2.719 +4.686 +7.342 -9.998 }}
Badness: 0.0202&lt;br /&gt;
* [[CWE]]: ~54/49 = 200.0000{{c}}, ~45/28 = 854.7144{{c}} (~36/35 = 54.7144{{c}})
&lt;br /&gt;
: error map: {{val| 0.000 +7.474 +13.686 -4.683 }}
&lt;a class="wiki_link" href="/triphi"&gt;Triforce(9) with L:s = phi&lt;/a&gt;&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=1| 18, 24, 42 }}
&lt;!-- ws:start:WikiTextHeadingRule:48:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc24"&gt;&lt;a name="Triforce-Semitriforce"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:48 --&gt;Semitriforce&lt;/h2&gt;
 
Commas: 49/48, 56/55, 77/75, 507/500&lt;br /&gt;
[[Badness]] (Sintel): 5.34
&lt;br /&gt;
 
POTE generator: ~7/6 = 246.642&lt;br /&gt;
=== 11-limit ===
&lt;br /&gt;
Subgroup: 2.3.5.7.11
Map: [&amp;lt;6 0 14 12 16 27|, &amp;lt;0 2 0 1 1 -1|]&lt;br /&gt;
 
EDOs: 6, 24, 54cd, 78cd, 102cdf&lt;br /&gt;
Comma list: 56/55, 128/125, 3773/3645
Badness: 0.0592&lt;br /&gt;
 
&lt;br /&gt;
Mapping: {{mapping| 6 1 14 4 8 | 0 2 0 3 3 }}
&lt;!-- ws:start:WikiTextHeadingRule:50:&amp;lt;h3&amp;gt; --&gt;&lt;h3 id="toc25"&gt;&lt;!-- ws:end:WikiTextHeadingRule:50 --&gt; &lt;/h3&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:52:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc26"&gt;&lt;a name="Hemiug"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:52 --&gt;Hemiug&lt;/h1&gt;
Optimal tunings:  
Commas: 128/125, 1323/1250&lt;br /&gt;
* WE: ~54/49 = 199.5188{{c}}, ~18/11 = 853.1623{{c}} (~36/35 = 55.0872{{c}})
&lt;br /&gt;
* CWE: ~54/49 = 200.0000{{c}}, ~18/11 = 854.3545{{c}} (~36/35 = 54.3545{{c}})
POTE generator: ~21/20 = 52.093&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=0| 18e, 24, 42e, 66ce, 108bccee }}
Map: [&amp;lt;3 1 7 14|, &amp;lt;0 2 0 -3|]&lt;br /&gt;
 
Wedgie: &amp;lt;&amp;lt;6 0 -9 -14 -31 -21||&lt;br /&gt;
Badness (Sintel): 2.67
EDOs: 21, 24, 45c, 69cd&lt;br /&gt;
 
Badness: 0.1378&lt;br /&gt;
== Niner ==
&lt;br /&gt;
Niner tempers out 686/675 and may be described as the {{nowrap| 9 & 27 }} temperament. Its ploidacot is enneaploid monocot. It gives 9 as the complexity of a [[harmonic seventh chord]], tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads. 27edo, [[36edo]] and [[63edo]] in the 63c val are among the possible tunings.
&lt;!-- ws:start:WikiTextHeadingRule:54:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc27"&gt;&lt;a name="Hemiug-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:54 --&gt;11-limit&lt;/h2&gt;
 
Commas: 56/55, 128/125, 1323/1250&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
&lt;br /&gt;
 
POTE generator: ~21/20 = 51.655&lt;br /&gt;
[[Comma list]]: 128/125, 686/675
&lt;br /&gt;
 
Map: [&amp;lt;3 1 7 14 16|, &amp;lt;0 2 0 -3 -3|]&lt;br /&gt;
{{Mapping|legend=1| 9 0 21 11 | 0 1 0 1 }}
EDOs: 21, 24, 69cd, 93cd&lt;br /&gt;
 
Badness: 0.0681&lt;br /&gt;
: mapping generators: ~49/45, ~3
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:56:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc28"&gt;&lt;a name="Hemiug-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:56 --&gt;13-limit&lt;/h2&gt;
[[Optimal tuning]]s:  
Commas: 56/55, 66/65, 105/104, 507/500&lt;br /&gt;
* [[WE]]: ~49/45 = 133.0272{{c}}, ~3/2 = 705.5438{{c}} (~36/35 = 40.4075{{c}})
&lt;br /&gt;
: [[error map]]: {{val| -2.755 +0.834 +7.259 -2.737 }}
POTE generator: ~21/20 = 51.548&lt;br /&gt;
* [[CWE]]: ~49/45 = 133.3333{{c}}, ~3/2 = 705.5157{{c}} (~36/35 = 38.8490{{c}})
&lt;br /&gt;
: error map: {{val| 0.000 +3.561 +13.686 +3.356 }}
Map: [&amp;lt;3 1 7 14 16 13|, &amp;lt;0 2 0 -3 -3 -1|]&lt;br /&gt;
 
EDOs: 21, 24, 69cdf, 93cdf&lt;br /&gt;
{{Optimal ET sequence|legend=1| 9, 18, 27, 63c, 90cc }}
Badness: 0.0423&lt;br /&gt;
 
&lt;br /&gt;
[[Badness]] (Sintel): 1.70
&lt;!-- ws:start:WikiTextHeadingRule:58:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc29"&gt;&lt;a name="Trug"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:58 --&gt;Trug&lt;/h1&gt;
 
Commas: 128/125, 360/343&lt;br /&gt;
=== 11-limit ===
&lt;br /&gt;
Subgroup: 2.3.5.7.11
POTE generator: ~48/35 = 501.980&lt;br /&gt;
 
&lt;br /&gt;
Comma list: 56/55, 128/125, 540/539
Map: [&amp;lt;3 1 7 6|, &amp;lt;0 3 0 2|]&lt;br /&gt;
 
EDOs: 9bd, 12&lt;br /&gt;
Mapping: {{mapping| 9 0 21 11 17 | 0 1 0 1 1 }}
Badness: 0.1383&lt;br /&gt;
 
&lt;br /&gt;
Optimal tunings:
&lt;!-- ws:start:WikiTextHeadingRule:60:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc30"&gt;&lt;a name="Oodako"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:60 --&gt;Oodako&lt;/h1&gt;
* WE: ~12/11 = 132.9553{{c}}, ~3/2 = 704.7217{{c}} (~36/35 = 39.9453{{c}})
Commas: 128/125, 2401/2400&lt;br /&gt;
* CWE: ~12/11 = 133.3333{{c}}, ~3/2 = 704.5723{{c}} (~36/35 = 37.9056{{c}})
&lt;br /&gt;
 
POTE generator: ~8/7 = 223.3540873874507317&lt;br /&gt;
{{Optimal ET sequence|legend=0| 9, 18e, 27e, 63cee }}
&lt;br /&gt;
 
Map: [&amp;lt;3 3 7 8|, &amp;lt;0 4 0 1|]&lt;br /&gt;
Badness (Sintel): 1.15
Wedgie: &amp;lt;&amp;lt;12 0 3 -28 -29 7||&lt;br /&gt;
 
EDOs: 6, 21, 27, 75c, 102cd, 129bcd&lt;br /&gt;
=== 13-limit ===
Badness: 0.1132&lt;br /&gt;
Subgroup: 2.3.5.7.11.13
&lt;br /&gt;
 
&lt;!-- ws:start:WikiTextHeadingRule:62:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc31"&gt;&lt;a name="Oodako-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:62 --&gt;11-limit&lt;/h2&gt;
Comma list: 56/55, 78/77, 91/90, 128/125
Commas: 56/55, 128/125, 3773/3750&lt;br /&gt;
 
&lt;br /&gt;
Mapping: {{mapping| 9 0 21 11 17 19 | 0 1 0 1 1 1 }}
POTE generator: ~8/7 = 223.019&lt;br /&gt;
 
&lt;br /&gt;
Optimal tunings:
Map: [&amp;lt;3 3 7 8 10|, &amp;lt;0 4 0 1 1|]&lt;br /&gt;
* WE: ~14/13 = 133.0143{{c}}, ~3/2 = 705.1969{{c}} (~36/35 = 40.1256{{c}})
EDOs: 6, 21, 27e&lt;br /&gt;
* CWE: ~14/13 = 133.3333{{c}}, ~3/2 = 705.0176{{c}} (~36/35 = 38.3510{{c}})
Badness: 0.0592&lt;br /&gt;
 
&lt;br /&gt;
{{Optimal ET sequence|legend=0| 9, 18e, 27e }}
&lt;!-- ws:start:WikiTextHeadingRule:64:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc32"&gt;&lt;a name="Oodako-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:64 --&gt;13-limit&lt;/h2&gt;
 
Commas: 56/55, 78/77, 128/125, 507/500&lt;br /&gt;
Badness (Sintel): 0.998
&lt;br /&gt;
 
POTE generator: ~8/7 = 223.449&lt;br /&gt;
== Trug ==
&lt;br /&gt;
Trug tempers out 360/343. It is generated by an interval of ~48/35, tuned very close to a perfect fourth, but the perfect fourth is mapped to three generator steps and a period. Its ploidacot is triploid alpha-tricot. 12edo is about as accurate as it can be tuned.  
Map: [&amp;lt;3 3 7 8 10 12|, &amp;lt;0 4 0 1 1 -2|]&lt;br /&gt;
 
EDOs: 6, 21, 27e&lt;br /&gt;
[[Subgroup]]: 2.3.5.7
Badness: 0.0423&lt;br /&gt;
 
&lt;br /&gt;
[[Comma list]]: 128/125, 360/343
&lt;!-- ws:start:WikiTextHeadingRule:66:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc33"&gt;&lt;a name="Hemisemiaug"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:66 --&gt;Hemisemiaug&lt;/h1&gt;
 
Commas: 128/125, 12005/11664&lt;br /&gt;
{{Mapping|legend=1| 3 1 7 6 | 0 3 0 2 }}
&lt;br /&gt;
 
POTE generator: ~15/14 = 144.515&lt;br /&gt;
: mapping generators: ~5/4, ~48/35
&lt;br /&gt;
 
Map: [&amp;lt;6 1 14 4|, &amp;lt;0 2 0 3|]&lt;br /&gt;
[[Optimal tuning]]s:  
Wedgie: &amp;lt;&amp;lt;12 0 18 -28 -5 42||&lt;br /&gt;
* [[WE]]: ~5/4 = 398.2337{{c}}, ~48/35 = 499.7635{{c}} (~15/14 = 101.5299{{c}})
Edos: 18, 24, 42, 66c, 108bc&lt;br /&gt;
: [[error map]]: {{val| -2.755 +0.834 +7.259 -2.737 }}
Badness: 0.2110&lt;br /&gt;
* [[CWE]]: ~5/4 = 400.0000{{c}}, ~48/35 = 500.9654{{c}} (~15/14 = 100.9654{{c}})
&lt;br /&gt;
: error map: {{val| 0.000 +3.561 +13.686 +3.356 }}
&lt;!-- ws:start:WikiTextHeadingRule:68:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc34"&gt;&lt;a name="Hemisemiaug-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:68 --&gt;11-limit&lt;/h2&gt;
 
Commas: 56/55, 128/125, 3773/3645&lt;br /&gt;
{{Optimal ET sequence|legend=1| 3b, 9bd, 12 }}
&lt;br /&gt;
 
POTE generator: ~15/14 = 144.780&lt;br /&gt;
[[Badness]] (Sintel): 3.50
&lt;br /&gt;
 
Map: [&amp;lt;6 1 14 4 8|, &amp;lt;0 2 0 3 3|]&lt;br /&gt;
== External links ==
EDOs: 24, 42e, 66ce, 108bce&lt;br /&gt;
* [https://web.archive.org/web/20211201070113/https://www.prismnet.com/~hmiller/music/temp-augmented.html Herman Miller's page about augmented temperament]
Badness: 0.0807&lt;br /&gt;
 
&lt;br /&gt;
[[Category:Temperament families]]
&lt;!-- ws:start:WikiTextHeadingRule:70:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc35"&gt;&lt;a name="Niner"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:70 --&gt;Niner&lt;/h1&gt;
[[Category:Pages with mostly numerical content]]
Niner gives 9 as the complexity of an otonal tetrad, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads.&lt;br /&gt;
[[Category:Augmented family| ]] <!-- main article -->
&lt;br /&gt;
[[Category:Rank 2]]
Commas: 128/125, 686/675&lt;br /&gt;
&lt;br /&gt;
POTE generator: ~3/2 = 707.167&lt;br /&gt;
&lt;br /&gt;
Map: [&amp;lt;9 0 21 11|, &amp;lt;0 1 0 1|]&lt;br /&gt;
Wedgie: &amp;lt;&amp;lt;9 0 9 -21 -11 21||&lt;br /&gt;
EDOs: 9, 18, 27, 63c, 90c&lt;br /&gt;
Badness: 0.0672&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:72:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc36"&gt;&lt;a name="Niner-11-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:72 --&gt;11-limit&lt;/h2&gt;
Commas: 56/55, 128/125, 540/539&lt;br /&gt;
&lt;br /&gt;
POTE generator: ~3/2 = 706.726&lt;br /&gt;
&lt;br /&gt;
Map: [&amp;lt;9 0 21 11 17|, &amp;lt;0 1 0 1 1|]&lt;br /&gt;
EDOs: 9, 27e, 36, 63ce&lt;br /&gt;
Badness: 0.0349&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:74:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc37"&gt;&lt;a name="Niner-13-limit"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:74 --&gt;13-limit&lt;/h2&gt;
Commas: 56/55, 78/77, 91/90, 128/125&lt;br /&gt;
&lt;br /&gt;
POTE generator: ~3/2 = 706.889&lt;br /&gt;
&lt;br /&gt;
Map: [&amp;lt;9 0 21 11 17 19|, &amp;lt;0 1 0 1 1 1|]&lt;br /&gt;
EDOs: 9, 27e, 36, 63ce&lt;br /&gt;
Badness: 0.0241&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:76:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc38"&gt;&lt;a name="Niner-Music"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:76 --&gt;Music&lt;/h2&gt;
&lt;a class="wiki_link_ext" href="https://www.prismnet.com/~hmiller/music/temp-augmented.html" rel="nofollow"&gt;Herman Miller's page about augmented temperament&lt;/a&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>

Latest revision as of 16:58, 21 August 2025

This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.

The augmented family of temperaments tempers out the diesis a.k.a. augmented comma, 128/125, the amount by which three 5/4 major thirds fall short of an octave, and so identifies the major third with the 1/3-octave. Hence it has the same 400-cent 5/4-approximations as 12edo.

Augmented

The period is 1/3 octave, and this is what is used for 5/4, the classical major third. The generator can be taken as a fifth or a semitone, and 12edo, with its excellent fifth, is an obvious tuning for 5-limit augmented, though a sharper fifth might be preferred to go with the sharp third. Its ploidacot is triploid monocot.

Subgroup: 2.3.5

Comma list: 128/125

Mapping: [⟨3 0 7], ⟨0 1 0]]

mapping generators: ~5/4, ~3

Optimal tunings:

  • WE: ~5/4 = 399.0128 ¢, ~3/2 = 704.8937 ¢ (~16/15 = 93.1320 ¢)
error map: ⟨-2.962 -0.023 +6.776]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 705.0691 ¢ (~16/15 = 94.9309 ¢)
error map: ⟨0.000 +3.114 +13.686]

Optimal ET sequence: 3, 9, 12, 27, 39, 51c, 90cc

Badness (Sintel): 0.523

Overview to extensions

The second comma of the normal comma list defines which 7-limit family member we are looking at. Augene adds 64/63, august 36/35, hexe 256/245, hemiaug 245/243, and triforce 49/48. Hexe splits the period to 1/6 octave, and hemiaug the generator, giving quartertones instead of semitones.

Augene

Main article: Augene

Augene tempers out 64/63 and 126/125. It may be described as the 12 & 15 temperament. 27edo and 39edo in the 39d val make for good tunings.

Subgroup: 2.3.5.7

Comma list: 64/63, 126/125

Mapping: [⟨3 0 7 18], ⟨0 1 0 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.7461 ¢, ~3/2 = 707.0335 ¢ (~21/20 = 90.4587 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 709.3249 ¢ (~21/20 = 90.6751 ¢)
error map: ⟨0.000 +7.370 +13.686 +12.524]

Optimal ET sequence: 12, 27, 39d, 66cd

Badness (Sintel): 0.628

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 64/63, 100/99

Mapping: [⟨3 0 7 18 20], ⟨0 1 0 -2 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.4962 ¢, ~3/2 = 708.5030 ¢ (~21/20 = 88.4895 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 711.6031 ¢ (~21/20 = 88.3969 ¢)

Optimal ET sequence: 12, 15, 27e

Badness (Sintel): 0.648

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 40/39, 56/55, 64/63, 66/65

Mapping: [⟨3 0 7 18 20 16], ⟨0 1 0 -2 -2 -1]]

Optimal tunings:

  • WE: ~5/4 = 398.0488 ¢, ~3/2 = 708.5402 ¢ (~21/20 = 87.5574 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.6704 ¢ (~21/20 = 87.3296 ¢)

Optimal ET sequence: 12f, 15, 27eff

Badness (Sintel): 0.859

Ogene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 91/90, 100/99

Mapping: [⟨3 0 7 18 20 -8], ⟨0 1 0 -2 -2 4]]

Optimal tunings:

  • WE: ~5/4 = 398.6473 ¢, ~3/2 = 710.1987 ¢ (~21/20 = 87.0959 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 712.5057 ¢ (~21/20 = 87.4943 ¢)

Optimal ET sequence: 12, 15, 27e, 69bceef

Badness (Sintel): 0.946

Agene

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 64/63, 78/77, 100/99

Mapping: [⟨3 0 7 18 20 35], ⟨0 1 0 -2 -2 -5]]

Optimal tunings:

  • WE: ~5/4 = 398.5229 ¢, ~3/2 = 707.0562 ¢ (~21/20 = 89.9897 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 710.1903 ¢ (~21/20 = 89.8097 ¢)

Optimal ET sequence: 12f, 27e, 66cdeeef

Badness (Sintel): 0.955

Eugene

Subgroup: 2.3.5.7.11

Comma list: 55/54, 64/63, 77/75

Mapping: [⟨3 0 7 18 -4], ⟨0 1 0 -2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.1743 ¢, ~3/2 = 712.6763 ¢ (~21/20 = 85.6723 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 713.9414 ¢ (~21/20 = 86.0586 ¢)

Optimal ET sequence: 12e, 15, 27, 42

Badness (Sintel): 1.18

August

August tempers out 36/35 and 225/224. It may be described as the 9 & 12 temperament. Unlike augene, august calls for a flat tuning of the fifth, and besides 12edo, 21edo is among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 36/35, 128/125

Mapping: [⟨3 0 7 -1], ⟨0 1 0 2]]

Optimal tunings:

  • WE: ~5/4 = 399.1036 ¢, ~3/2 = 694.4509 ¢ (~16/15 = 103.7564 ¢)
error map: ⟨-2.689 -10.193 +7.412 +15.594]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 694.6812 ¢ (~16/15 = 105.3188 ¢)
error map: ⟨0.000 -7.274 +13.686 +20.537]

Optimal ET sequence: 9, 12, 45cd

Badness (Sintel): 0.670

11-limit

Subgroup: 2.3.5.7.11

Comma list: 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1], ⟨0 1 0 2 2]]

Optimal tunings:

  • WE: ~5/4 = 398.9225 ¢, ~3/2 = 690.6486 ¢ (~16/15 = 107.1966 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 690.8519 ¢ (~16/15 = 109.1481 ¢)

Optimal ET sequence: 9, 12, 21, 33e

Badness (Sintel): 0.668

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 27/26, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 -3], ⟨0 1 0 2 2 3]]

Optimal tunings:

  • WE: ~5/4 = 399.0956 ¢, ~3/2 = 687.2261 ¢ (~16/15 = 110.9651 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 687.5057 ¢ (~16/15 = 112.4943 ¢)

Optimal ET sequence: 9, 12f, 21, 33ef

Badness (Sintel): 0.762

Augustus

Subgroup: 2.3.5.7.11.13

Comma list: 26/25, 36/35, 45/44, 56/55

Mapping: [⟨3 0 7 -1 1 11], ⟨0 1 0 2 2 0]]

Optimal tunings:

  • WE: ~5/4 = 400.4230 ¢, ~3/2 = 686.0809 ¢ (~16/15 = 114.7650 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 685.8446 ¢ (~16/15 = 114.1554 ¢)

Optimal ET sequence: 9, 12

Badness (Sintel): 0.919

Inflated

Subgroup: 2.3.5.7

Comma list: 28/27, 128/125

Mapping: [⟨3 0 7 -6], ⟨0 1 0 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4023 ¢, ~3/2 = 719.8327 ¢ (~25/24 = 76.9719 ¢)
error map: ⟨-3.762 +1.317 +4.909 +2.060]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 721.0196 ¢ (~25/24 = 78.9804 ¢)
error map: ⟨0.000 +19.065 +13.686 -5.767]

Optimal ET sequence: 3d, 12d, 15

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 28/27, 55/54, 128/125

Mapping: [⟨3 0 7 -6 -4], ⟨0 1 0 3 3]]

Optimal tunings:

  • WE: ~5/4 = 398.4016 ¢, ~3/2 = 719.7758 ¢ (~25/24 = 77.0275 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 720.9386 ¢ (~25/24 = 79.0614 ¢)

Optimal ET sequence: 3de, 12de, 15

Badness (Sintel): 1.03

Deflated

Subgroup: 2.3.5.7

Comma list: 21/20, 128/125

Mapping: [⟨3 0 7 13], ⟨0 1 0 -1]]

Optimal tunings:

  • WE: ~5/4 = 401.9566 ¢, ~3/2 = 684.9634 ¢ (~16/15 = 118.9497 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 682.2587 ¢ (~16/15 = 117.7413 ¢)
error map: ⟨0.000 -19.696 +13.686 -51.085]

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.50

11-limit

Subgroup: 2.3.5.7.11

Comma list: 21/20, 33/32, 128/125

Mapping: [⟨3 0 7 13 15], ⟨0 1 0 -1 -1]]

Optimal tunings:

  • WE: ~5/4 = 402.1799 ¢, ~3/2 = 683.7477 ¢ (~16/15 = 120.6120 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~3/2 = 680.0162 ¢ (~16/15 = 119.9838 ¢)

Optimal ET sequence: 3, 6b, 9

Badness (Sintel): 1.23

Hexe

Hexe tempers out 50/49 and may be described as 6 & 12, viewed as 6et with an independent generator for prime 3. Its ploidacot is hexaploid monocot.

Subgroup: 2.3.5.7

Comma list: 50/49, 128/125

Mapping: [⟨6 0 14 17], ⟨0 1 0 0]]

mapping generators: ~28/25, ~3

Optimal tunings:

  • WE: ~28/25 = 199.0488 ¢, ~3/2 = 707.5815 ¢ (~25/24 = 88.6137 ¢)
error map: ⟨+5.870 -11.122 +27.382 -34.224]
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 708.6907 ¢ (~25/24 = 91.3093 ¢)
error map: ⟨0.000 +6.735 +13.686 +31.174]

Optimal ET sequence: 6, 12, 30d, 42dd, 54cdd

Badness (Sintel): 1.46

11-limit

Subgroup: 2.3.5.7.11

Comma list: 50/49, 56/55, 125/121

Mapping: [⟨6 0 14 17 21], ⟨0 1 0 0 0]]

Optimal tunings:

  • WE: ~28/25 = 198.6942 ¢, ~3/2 = 709.6404 ¢ (~25/24 = 85.1362 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 711.8043 ¢ (~25/24 = 88.1957 ¢)

Optimal ET sequence: 6, 12, 30dee, 42ddeee

Badness (Sintel): 1.27

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 50/49, 56/55, 66/65, 105/104

Mapping: [⟨6 0 14 17 21 13], ⟨0 1 0 0 0 1]]

Optimal tunings:

  • WE: ~28/25 = 198.4492 ¢, ~3/2 = 704.4994 ¢ (~25/24 = 89.2973 ¢)
  • CWE: ~28/25 = 200.0000 ¢, ~3/2 = 706.6050 ¢ (~16/15 = 93.3950 ¢)

Optimal ET sequence: 6f, 12f

Badness (Sintel): 1.49

Triforce

triforce9.jpg
Lattice of triforce

Triforce tempers out 49/48 and may be described as 9 & 15. Its ploidacot is triploid alpha-dicot. 24edo and 39edo are among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 49/48, 128/125

Mapping: [⟨3 0 7 6], ⟨0 2 0 1]]

mapping generators: ~5/4, ~7/4

Optimal tunings:

  • WE: ~5/4 = 399.7480 ¢, ~7/4 = 952.3507 ¢ (~35/32 = 152.8547 ¢)
error map: ⟨-0.756 +2.746 +11.922 -17.987]
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7463 ¢ (~35/32 = 152.7463 ¢)
error map: ⟨0.000 +3.538 +13.686 -16.080]

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 1.39

11-limit

Subgroup: 2.3.5.7.11

Comma list: 49/48, 56/55, 77/75

Mapping: [⟨3 0 7 6 8], ⟨0 2 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 399.7654 ¢, ~7/4 = 952.3730 ¢ (~12/11 = 152.8421 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 952.7447 ¢ (~12/11 = 152.7447 ¢)

Optimal ET sequence: 6, 9, 15, 24, 39

Badness (Sintel): 0.865

Music

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 66/65, 77/75

Mapping: [⟨3 0 7 6 8 4], ⟨0 2 0 1 1 3]]

Optimal tunings:

  • WE: ~5/4 = 399.7107 ¢, ~7/4 = 950.9983 ¢ (~12/11 = 151.5768 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~7/4 = 951.4465 ¢ (~12/11 = 151.4465 ¢)

Optimal ET sequence: 6f, 9, 15, 24

Badness (Sintel): 0.837

Scales
  • triphi, Triforce[9] with L:s = phi

Semitriforce

This extension splits the period into 1/6-octave for ~44/39. Its ploidacot is hexaploid dicot.

Subgroup: 2.3.5.7.11.13

Comma list: 49/48, 56/55, 77/75, 507/500

Mapping: [⟨6 0 14 12 16 27], ⟨0 2 0 1 1 -1]]

mapping generators: ~44/39, ~7/4

Optimal tunings:

  • WE: ~44/39 = 199.8321 ¢, ~7/4 = 952.5580 ¢ (~40/39 = 46.6024 ¢)
  • CWE: ~44/39 = 200.0000 ¢, ~7/4 = 953.2005 ¢ (~40/39 = 46.7995 ¢)

Optimal ET sequence: 6, 18bd, 24

Badness (Sintel): 2.44

Hemiaug

Hemiaug tempers out 245/243 and may be described as 24 & 27. The generator may be taken as ~14/9, but also a neutral third or a neutral second that stand in for 11/9~16/13 and 12/11~13/12 in the higher limits, respectively. Hemiaug's ploidacot is triploid dicot. 27edo makes for a recommendable tuning in the 7-limit, but 51edo serves better in the higher limits.

Subgroup: 2.3.5.7

Comma list: 128/125, 245/243

Mapping: [⟨3 1 7 -1], ⟨0 2 0 5]]

mapping generators: ~5/4, ~14/9

Optimal tunings:

  • WE: ~5/4 = 398.9278 ¢, ~14/9 = 752.8583 ¢ (~36/35 = 44.9973 ¢)
error map: ⟨-3.217 +2.689 +6.181 -3.462]
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 754.2078 ¢ (~36/35 = 45.7922 ¢)
error map: ⟨0.000 +6.461 +13.686 +2.213]

Optimal ET sequence: 24, 27

Badness (Sintel): 1.78

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 243/242

Mapping: [⟨3 1 7 -1 1], ⟨0 2 0 5 5]]

Optimal tunings:

  • WE: ~5/4 = 398.8946 ¢, ~14/9 = 752.1272 ¢ (~36/35 = 45.6619 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.5000 ¢ (~36/35 = 46.5000 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.26

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 91/90, 128/125, 243/242

Mapping: [⟨3 1 7 -1 1 13], ⟨0 2 0 5 5 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.1053 ¢, ~14/9 = 752.0643 ¢ (~36/35 = 46.1463 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~14/9 = 753.3806 ¢ (~36/35 = 46.6194 ¢)

Optimal ET sequence: 24, 27e, 51ce

Badness (Sintel): 1.25

Hemiug

Hemiug tempers out 1323/1250 and may be described as 21 & 24. The generator is a similar interval but for ~32/21 instead of ~14/9, and the ploidacot is triploid dicot, the same as hemiaug.

Subgroup: 2.3.5.7

Comma list: 128/125, 1323/1250

Mapping: [⟨3 1 7 14], ⟨0 2 0 -3]]

mapping generators: ~5/4, ~32/21

Optimal tunings:

  • WE: ~5/4 = 400.1805 ¢, ~32/21 = 748.2436 ¢ (~21/20 = 52.1174 ¢)
error map: ⟨+0.542 -5.287 +14.950 -11.030]
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 747.9138 ¢ (~21/20 = 52.0862 ¢)
error map: ⟨0.000 -6.127 +13.686 -12.567]

Optimal ET sequence: 21, 24, 45c

Badness (Sintel): 3.49

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 1323/1250

Mapping: [⟨3 1 7 14 16], ⟨0 2 0 -3 -3]]

Optimal tunings:

  • WE: ~5/4 = 400.0637 ¢, ~32/21 = 748.4638 ¢ (~33/32 = 51.6637 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.3383 ¢ (~33/32 = 51.6617 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 2.25

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 66/65, 105/104, 507/500

Mapping: [⟨3 1 7 14 16 13], ⟨0 2 0 -3 -3 -1]]

Optimal tunings:

  • WE: ~5/4 = 399.8855 ¢, ~32/21 = 748.2378 ¢ (~33/32 = 51.5332 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~32/21 = 748.4655 ¢ (~33/32 = 51.5345 ¢)

Optimal ET sequence: 21, 24

Badness (Sintel): 1.75

Oodako

Oodako tempers out 2401/2400 and may be described as 21 & 27. It is generated by a quarter of a fifth, which stands in for ~28/25. Its ploidacot is triploid tetracot.

Subgroup: 2.3.5.7

Comma list: 128/125, 2401/2400

Mapping: [⟨3 3 7 8], ⟨0 4 0 1]]

mapping generators: ~5/4, ~28/25

Optimal tunings:

  • WE: ~5/4 = 399.0296 ¢, ~28/25 = 176.2174 ¢ (~49/48 = 46.5949 ¢)
error map: ⟨-2.911 +0.004 +6.894 -0.371]
  • CWE: ~5/4 = 400.0000 ¢, ~28/25 = 176.2984 ¢ (~49/48 = 47.4031 ¢)
error map: ⟨0.000 +3.239 +13.686 +7.473]

Optimal ET sequence: 6, 21, 27, 75c, 102ccd, 129bccd

Badness (Sintel): 2.86

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 2401/2400

Mapping: [⟨3 3 7 8 10], ⟨0 4 0 1 1]]

Optimal tunings:

  • WE: ~5/4 = 398.6615 ¢, ~11/10 = 176.3886 ¢ (~49/48 = 45.8843 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.5471 ¢ (~49/48 = 46.9059 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.96

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 128/125, 507/500

Mapping: [⟨3 3 7 8 10 12], ⟨0 4 0 1 1 -2]]

Optimal tunings:

  • WE: ~5/4 = 398.8612 ¢, ~11/10 = 176.0486 ¢ (~49/48 = 46.7640 ¢)
  • CWE: ~5/4 = 400.0000 ¢, ~11/10 = 176.3326 ¢ (~49/48 = 47.3348 ¢)

Optimal ET sequence: 6, 21, 27e

Badness (Sintel): 1.75

Hemisemiaug

Hemisemiaug tempers out 12005/11664 and splits both the period and generator of augmented in two. Its ploidacot is hexaploid alpha-dicot.

Subgroup: 2.3.5.7

Comma list: 128/125, 12005/11664

Mapping: [⟨6 1 14 4], ⟨0 2 0 3]]

mapping generators: ~54/49, ~45/28

Optimal tunings:

  • WE: ~54/49 = 199.5469 ¢, ~45/28 = 853.5468 ¢ (~36/35 = 55.3594 ¢)
error map: ⟨-2.719 +4.686 +7.342 -9.998]
  • CWE: ~54/49 = 200.0000 ¢, ~45/28 = 854.7144 ¢ (~36/35 = 54.7144 ¢)
error map: ⟨0.000 +7.474 +13.686 -4.683]

Optimal ET sequence: 18, 24, 42

Badness (Sintel): 5.34

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 3773/3645

Mapping: [⟨6 1 14 4 8], ⟨0 2 0 3 3]]

Optimal tunings:

  • WE: ~54/49 = 199.5188 ¢, ~18/11 = 853.1623 ¢ (~36/35 = 55.0872 ¢)
  • CWE: ~54/49 = 200.0000 ¢, ~18/11 = 854.3545 ¢ (~36/35 = 54.3545 ¢)

Optimal ET sequence: 18e, 24, 42e, 66ce, 108bccee

Badness (Sintel): 2.67

Niner

Niner tempers out 686/675 and may be described as the 9 & 27 temperament. Its ploidacot is enneaploid monocot. It gives 9 as the complexity of a harmonic seventh chord, tying it with augene as a temperament supported by 27edo. Niner[18], therefore, has nine such tetrads. 27edo, 36edo and 63edo in the 63c val are among the possible tunings.

Subgroup: 2.3.5.7

Comma list: 128/125, 686/675

Mapping: [⟨9 0 21 11], ⟨0 1 0 1]]

mapping generators: ~49/45, ~3

Optimal tunings:

  • WE: ~49/45 = 133.0272 ¢, ~3/2 = 705.5438 ¢ (~36/35 = 40.4075 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~49/45 = 133.3333 ¢, ~3/2 = 705.5157 ¢ (~36/35 = 38.8490 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 9, 18, 27, 63c, 90cc

Badness (Sintel): 1.70

11-limit

Subgroup: 2.3.5.7.11

Comma list: 56/55, 128/125, 540/539

Mapping: [⟨9 0 21 11 17], ⟨0 1 0 1 1]]

Optimal tunings:

  • WE: ~12/11 = 132.9553 ¢, ~3/2 = 704.7217 ¢ (~36/35 = 39.9453 ¢)
  • CWE: ~12/11 = 133.3333 ¢, ~3/2 = 704.5723 ¢ (~36/35 = 37.9056 ¢)

Optimal ET sequence: 9, 18e, 27e, 63cee

Badness (Sintel): 1.15

13-limit

Subgroup: 2.3.5.7.11.13

Comma list: 56/55, 78/77, 91/90, 128/125

Mapping: [⟨9 0 21 11 17 19], ⟨0 1 0 1 1 1]]

Optimal tunings:

  • WE: ~14/13 = 133.0143 ¢, ~3/2 = 705.1969 ¢ (~36/35 = 40.1256 ¢)
  • CWE: ~14/13 = 133.3333 ¢, ~3/2 = 705.0176 ¢ (~36/35 = 38.3510 ¢)

Optimal ET sequence: 9, 18e, 27e

Badness (Sintel): 0.998

Trug

Trug tempers out 360/343. It is generated by an interval of ~48/35, tuned very close to a perfect fourth, but the perfect fourth is mapped to three generator steps and a period. Its ploidacot is triploid alpha-tricot. 12edo is about as accurate as it can be tuned.

Subgroup: 2.3.5.7

Comma list: 128/125, 360/343

Mapping: [⟨3 1 7 6], ⟨0 3 0 2]]

mapping generators: ~5/4, ~48/35

Optimal tunings:

  • WE: ~5/4 = 398.2337 ¢, ~48/35 = 499.7635 ¢ (~15/14 = 101.5299 ¢)
error map: ⟨-2.755 +0.834 +7.259 -2.737]
  • CWE: ~5/4 = 400.0000 ¢, ~48/35 = 500.9654 ¢ (~15/14 = 100.9654 ¢)
error map: ⟨0.000 +3.561 +13.686 +3.356]

Optimal ET sequence: 3b, 9bd, 12

Badness (Sintel): 3.50

External links

Retrieved from "https://en.xen.wiki/index.php?title=Augmented_family&oldid=207920"