Extended-diatonic interval names
Besides the octave, which is treated as an interval of equivalence in almost all musics globally, the perfect fifth and perfect fourth are strongest consonances. Reasonable approximations to those intervals that can be found by dividing the octave equally into 5 notes, or into 7 notes, and excellent approximations can be found by dividing the octave equally into 12 notes (corresponding to the system of 12-tone equal temperament that sees persistent global use today). Given this, along with the limited capacity of human short-term memory, pentatonic and heptatonic (5-note and 7-note) scales are extremely common, from antiquity, to, again, almost all musics globally. The heptatonic scale in which the most number of perfect fifths and fourths is called the diatonic scale, and of all pentatonic or heptatonic scales has seen more application as a basis for music notation and interval names. This article details the development of Western diatonic-based interval names. Where today a small number of competing diatonic-based interval naming schemes exist for the description of microtonal music (music that is not tuned to 12-tone Equal Temperament (12-tET), a critical review of current proposed schemes is also undertaken.
The origin of diatonic interval names

Music theory describing the use of heptatonic-diatonic scales, including interval names, has been traced back as far as 2000BC, deciphered from a Sumerian cuneiform tablet from Nippur by Kilmer (1986). From Kummel (1970) we know that 'the names given to the seven tunings/scales were derived from the specific intervals on which the tuning procedure started' (Kilmer, 1986). This formed the basis of their musical notation (Kilmer, 2016). The table to the right following table displays the Ancient Mesopotamian interval names accompanied by their modern names.
Kilmer also writes that 'the ancient Mesopotamian musicians/“musicologists” knew what we call today the Pythagorean series of fifths, and that the series could be accomplished within a single octave by means of “inversion” '. The Mesopotamian's music and theory was passed down through the Babylonians and the Assyrians to the Ancient Greeks, as well as their mathematics, particularly concerning musical and acoustical sound ratios (Ibid, Hodgekin, 2005).
Such mathematical and musical ideas are attributed to Pythagoras, who undoubtedly made them popular., although many scholars suggest he may have learned these ideas from his Babylonian and Egyptian mentors. Nonetheless, Pythagoras' idea that that by dividing the length of a string into ratios of halves, thirds, quarters and fifths created the musical intervals of an octave, a perfect fifth, an octave again, and a major third form the basis of Ancient Greek music theory (http://www.historyofmusictheory.com/?page_id=20). His tuning of the diatonic scale by only octaves and perfect fifths (Pythagorean tuning) is influential through to today.
Ancient Greek interval names
Intervals in Ancient Greek music were written either as string length ratios, after Pythagoras, or as positions in a tetrachord.
2/1, the octave was named diapason meaning 'through all [strings]'
3/2, the perfect fifth was labelled diapente, meaning 'through 5 [strings]'
4/3, the perfect fourth, was labelled diatessaron, meaning 'through 4 [strings]'
dieses, 'sending through', refers to any interval smaller than about 1/3 of a perfect fourth
tonos referred both to the interval of a whole tone, and something more akin to mode or key in the modern sense (Chalmers, 1993)
ditone referred to the interval made by stacking two 9/8 whole tones, resulting in 81/64, the Pythagorean major third. (Monzo, http://www.tonalsoft.com)
256/243 - the limma, which is the ratio between left over after subtracting two 9/8 tones (together making a ditone) a perfect fourth, the diatonic semitone of the Pythagorean diatonic scale
2187/2048 - the apotome, which is the ratio between the tone and the limma, the chromatic semitone of the Pythagorean diatonic scale
The Ancient Greek term diatonon, meaning 'through tones', refers to the genus with two whole tones and a semitone, or any genus in which no interval is greater than one half of the fourth (Chalmers, 1993). The Pythaogrean diatonic scale is the scale that may be built from one two Pythagorean tetrachords, and the left over interval of 9/8.
Zarlino and meantone
Intervals were referred to by the Ancient Greek names through the 18th century, as Latin names. By the Renaissance it had been discovered that a Pythagorean diminished fourth sounded sweet, and approximated the string length ratio 5/4. This just tuning for the major third was sought after, along with the complementary 6/5 tuning for the minor third, and octave complements to both - 8/5 for the minor sixth and 5/3 for the major sixth. Influential Italian music theorist and composer Gioseffo Zarlino put forth that choirs tuned the diatonic scale to the tuning built from this tetrachord, the intense diatonic scale, also known as the syntonic or syntonus diatonic scale or the Ptolemaic sequence:
1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1
Included in this scale, however, were wolf intervals: imperfect consonances that occurred as tunings of the same interval as perfect consonances. For example, between 1/1 and 3/2, 4/3 and 1/1, 5/3 and 5/4; and 5/4 and 15/8 occurs the perfect fifth, 3/2, whereas between 9/8 and 5/3 occurs the wolf fifth, 40/27, flat of 3/2 by 81/80. This was also the interval by which four 3/2 fifths missed 5/1 (the interval two octaves above 5/4). It was named the syntonic comma after Ptolemy's syntonus or intense diatonic tetrachord which consists of the intervals 9/8, 10/9 and 16/15, where 9/8 and 10/9 differ by this interval. By making the syntonic comma a unison the wolf fifth could be made a perfect fifth. It was discovered that this could be achieved by flattening (tempering) the perfect fifth by some fraction of this comma such that four of these fifths less two octaves gave an approximation of 5/4. Where two fifths less an octave give 9/8, the next two add another 10/9 to result in the 5/4. 9/8 and 10/9 were referred to as the major tone (tunono maggiore) and minor tone (tunono minore), respectively, and where this tuning led to them being equated, it was referred to as Meantone temperament, which is said to 'temper out' the syntonic comma. Zarlino advocated the flattening of the fifth by 2/7 of a comma, leading to 2/7-comma meantone, but also described 1/3-comma and 1/4-comma Meantone as usable (Zarlino, 1558).
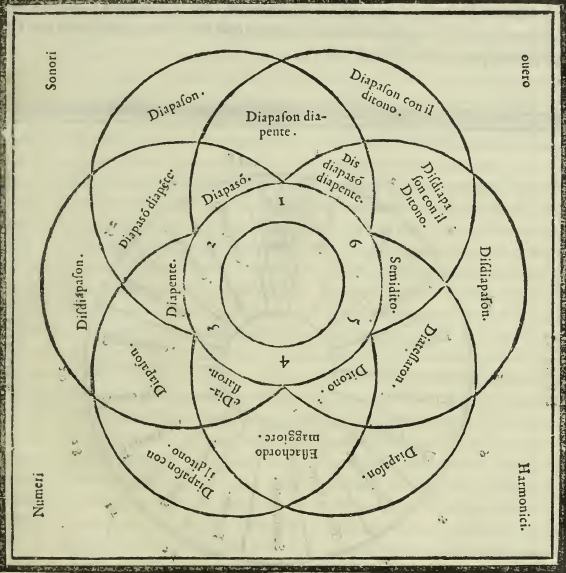
The diagram on the right, from Zarlino's 1558 treatise Le istitutioni harmoniche associates many intervals with their tuning as perfect consonances. The perfect tuning for the ditone was considered then to be 5/4, rather than 81/64. The minor third, referred to as a semiditone (labelled also in Le istitutioni harmoniche by as Trihemituono) was considered to be 6/5, and not 32/27. Additionally the semitone possessed two alternative perfect tunings: 16/15, the difference between 15/8 and 2/1, or 5/4 and 4/3, and 25/24, the difference between 6/5 and 5/4. 16/15 was referred to as the major semitone (semituono maggiore) and 25/24 as the minor semitone (semituono minore).
In addition to the Latin interval names, derived from the Ancient Greek interval names, we see on the diagram a single interval name in Italian: Essachordo maggiore, referring to the ratio 5/3. Chapter 16 of Part 1, Quel che sia Consonanze semplice, e Composta; & che nel Senario si ritouano le sorme di tutte le somplici consonanze; & onde habbia origine l'Essachordo minore, puts forward that the Essachordo minore, be tuned to 8/5.
In Part 3, Zarlino writes that the Unison, Fourth, Fifth and Octave (and, by extension, 11th, 12th, 15th, 18th, 19th and 22nd) are considered perfect consonances, and that Thirds and Sixths (and, by extension, 10ths, 13ths, 17ths and 20ths) are considered imperfect consonances, after Aristotle. Seconds, Sevenths (and, by extension, 9ths, 14ths, 16ths and 21sts) are considered dissonances. He adds that the imperfect consonances come in two types, 'maggiore' and 'minore', where, for each interval class, the minor is the smaller interval, and the major, the larger, defining therefore, the ditone and essachord as the major Third and Sixth respectively, and the semiditone and minor essachord as the minor Third and Sixth. The major and minor Seconds are then equated to the tone and semitone. Here we begin to see today's interval names.
He adds further,
Et la Quarta è di tre sorti cioè la Diatessaron consonanza; il Tritono, che è una compositione di tre Tuoni; & la Semidiatessaron, che è una compositione di un Tuono, & di due Semituoni; i quali intervalli ne i loro estremi sono dissonanti. Questo istosso si potrebbe etiandio dire della Quinta, della Ottava, & della replicate, le quali si lassano per non andare in lungo.
defining the two 'extremely dissonant' other types of Fourth as the Tritono, consisting of three tones, and the Semidiatessaron, consisting of a tone and two semitones, and suggesting that similar could be said of the Fifth and Octave, and their (octave) replicates, but will not be, in order that he does not go on too much. These two dissonant fourths correspond to today's augmented and diminished fourth. If the definitions Zarlino alludes to for the fifth, octave and replicates were completed, they would define today's augmented and diminished fifth and octave, augmented unison, and other octave replicates.
In the 1691 Lettre de Monsieur Huygens à l'Auteur [Henri Basnage de Beauval] touchant le Cycle Harmonique, theorist Christiaan Huygens gave names and ratios to common intervals and mapped them to 31-tET, which very closely approximates 1/4-comma Meantone. Translated from French, 3/2 was labelled a Fifth, 4/3 a Fourth, 5/4 a major Third, 6/5 and minor Third, 5/3 a major Sixth and 8/5 a minor Sixth, we can see that these names and definitions match those of Zarlino.
English interval names in the Baroque

We see these names translated into English music theorist and mathematician Robert Smith's 1749 Harmonics, or, The Philosophy of Musical Sounds (referenced figures shown on the right):
Fig. 2. If a musical string CO and it's parts DO, EO, FO, GO, AO, BO, cO, be in proportion to one another as the numbers 1, 8/9, 4/5, 3/4, 2/3, 3/5, 8/15, 1/2, their vibrations will exhibit the system of 8 sounds which musicians donate by the letters C, D, E, F, G, A, B, c.
Fig. 3. And supposing those strings to be ranged like ordinates to a right line Cc, and their distances CD, DE, EF, FG, GA, AB, BC, not to be the differences of their lengths, as in fig. 2. but to be the magnitudes proportional to the intervals of their sounds, the received Names of these intervals are shewn in the following Table; and are taken from the numbers of the strings or sounds in each interval inclusively; as a Second, Third, Fourth, Fifth, &c, with the epithet of major or minor, according as the name or number belongs to a greater of smaller total interval; the difference of which results chiefly from the different magnitudes of the major and minor second, called the Tone and Hemitone.
In contrast to Zarlino and Huygens, Smith applies the 'major' and 'minor' qualifiers also to fourths and fifths. Where they, like all other intervals of the scale but octaves and unisons, come in two different sizes in the diatonic scale, we can see this is a more consistent scheme. I believe it to be unfortunate that Smith's scheme was not favoured over the names we saw first from Zarlino, which we see still today. Smith adds that
Any one of the ratios in the third column of the foregoing Table, except 80 to 81, or any one of them compounded once of oftener with the ratio 2 to 1 or 1 to 2, is called a Perfect ratio when reduced to it's least terms. And when the times of the single vibrations of any two sounds have a perfect ratio, the consonance and it's interval too after called Perfect; and is called Imperfect or Tempered when that perfect ratio and interval is a little increased or decreased.
...
Any small increment of decrement of a perfect interval is called respectively the Sharp or Flat Temperament of the imperfect consonance, and is measured most conveniently by the proportion it bears to the comma
Therefore, in this system 3/2 is the Perfect major Fifth and 5/4 the Perfect major Third. 81/64 might be labelled a comma sharp major Third, 32/27 a comma flat minor Third, and the 1/4-comma Meantone fifth a 1/4-comma flat major Fifth. The interval naming scheme Smith describes may be immediately applied to 5-limit microtonal systems. There is an inconsistency, however, where it seems that 9/8 should be called a Perfect major Second, but that, while 9/5 be named a comma sharp minor Seventh, it's inverse, 10/9, is a Perfect minor Tone.
In An Elementary Treatise on Musical Intervals and Temperament, published in 1876, R. H. M Bosanquet refers to 5/4 as the perfect third, and 81/64 as the Pythagorean third. Bosanquet also labels other intervals of the Pythagorean diatonic scale similarly, i.e. 256/243, the limma, is labelled the Pythagorean semitone, and 27/16 the Pythagorean sixth. 81/80 is labelled the ordinary comma, or simple the comma, and the Pythagorean comma is defined as the difference between twelve fifths and seven octaves. The apotome of 2187/2048 is referred to as Apatomè Pythagoria. The following relationships are then described:
Diatonic Semitone = Pythagorean Semitone + Comma
= Apatomè Pythagoria - Skhisma
Chromatic Semitone = Apatomè Pythagoria - Comma
= Pythagorean Semitone + Skhisma
Pythagorean Semitone = Comma + Skhisma
= Apatomè Pythagoria - Pythagorean Semitone
Helmholtz and Ellis
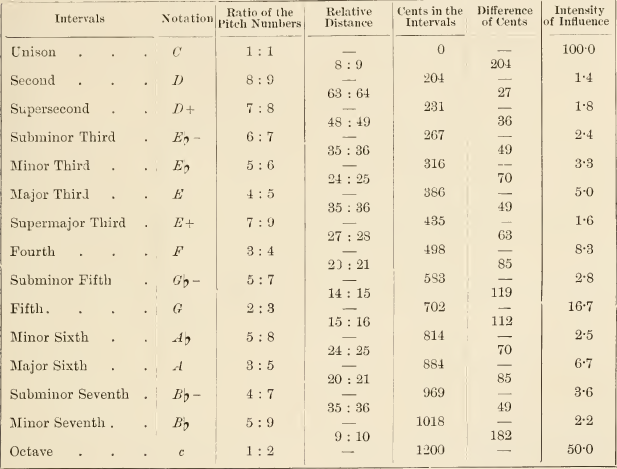
Through the investigations of Galileo (1638), Newton, Euler (1729), and Bernoulli (1771), theorist Hermann von Helmholtz was aware that ratios governing the lengths of strings existed also for the vibrations of the tones they produced. His investigation of the harmonic series associated with these ratios of vibration led him to the consideration of ratios above the 5-limit. In his seminal On the Sensations of Tone as a Physiological Basis for the Theory of Music, published in German in 1863 and translated into English in 1875 by Alexander Ellis, he listed just intervals as show in the table to the right. It is interesting to note that 8:9 is labelled a 'Second' rather than a 'major Second'. The minor Seventh is shown as 5:9 rather than as 9:16 seemingly because of the 9 partial limit imposed on the table. It is also worth noting that 5:7 is labelled a subminor Fifth. 'Super', indicated in notation with a '+', raises an interval by 35:36, the septimal quarter tone, and 'sub', indicated with a '-' lowers by the same interval with the exception of the Supersecond 7:8, which lies 63:64, the septimal comma above the Second. The subminor fifth is not included in this as no minor Fifth is shown. If we assume that 'sub' lowers an interval 35:36, then the minor Fifth would be 18:25, 80:81 above Smith's 45:64 minor Fifth, however in table 2 below, Ellis labels 18:25 a superfluous Fourth, and it's inverse, 25:32, an acute diminished Fifth, whilst 64:45 is labelled a diminished Fifth and its inverse 32:45 a false Fourth or Tritone. If we label 9:10 as a 'major Second', and 7:8 as a 'supermajor Second' then they differ by 35:36, the major Second is the inverse of the minor Seventh, and the supermajor Second is the octave inverse of the subminor Seventh. We can assume that Smith's 'major Fifth' and 'minor Fourth' names for 3/2 and 4/3 were not wholly taken up. We can add to this table the remaining octave inversions as well as the super Fourth and sub Fifth.
| Intervals | Notation | Ratio | Cents in the interval |
|---|---|---|---|
| Major Second | D | 9:10 | 182 |
| Sub Fourth | F- | 16:21 | 471 |
| Supermajor Fourth | F#+ | 7:10 | 617 |
| Super Fifth | G+ | 21:32 | 729 |
| Subminor Sixth | A♭- | 9:14 | 765 |
| Supermajor Sixth | A+ | 7:12 | 933 |
Helmholtz defined the perfect consonances as the Octave, Twelfth and Double Octave as well as Fourth and Fifth. The major Sixth and major Third are next called medial consonances, considered to in the era of Pythagorean tuning to be imperfect consonances, which Helmholtz defined instead to be the minor Third and the minor Sixth.
Regarding the tuning of the intervals however, those corresponding to simple ratios of vibration are, as in Smith, referred to as perfect, however hey are also described as 'justly-intoned', or by Ellis as 'just'. The perfect tuning for the semitone is listed as 16/15, or 112c. The perfect tunings are compared to the Pythagorean tunings, where the Pythagorean tuning of the major Third and sixth are described as 81/80 above the perfect tunings, and of the minor Third, minor Sixth and semitone to be 81/80 below the perfect tunings. Helmholtz notes that the Pythagorean tunings are closer to the equal tempered tunings than the perfect tunings. Helmholtz also describes the Pythagorean Tritone as of 612c.
Ellis includes an additional table providing names for many different just and tempered intervals, perfect and imperfect. The interval names do not appear to follow any sort of consistent naming system, rather intervals seem to be named case-by-case. They also largely do not correspond to the interval names used by Helmholtz.
In Notes on the Observations of Musical Beats, Proc. R. Soc. Lond. 1880, Ellis named many just intervals of the 7-limit (including 3 and 5-limit intervals):
Fifth 3:2, Fourth 4:3, Major Third 5:4, Minor Third 6:5, Major Sixth 5:3, Sub-Fifth 7:5, Super-Fourth 10:7, Super-major Third 9:7, Sub-minor Sixth 14:9, Sub-minor Third 7:6, Super-major Sixth 12:7, Sub-minor or Harmonic Seventh 7:4, Super-major Second 8:7, Major Tone 9:8, Minor Tone 10:9, Small Major Seventh 9:5 and Diatomic (sic.) Semitone 16:15
He later lists ‘The Major Sevenths 16:9 and 15:8’. The labeling of 16:9 as a Major Seventh and 9:5 as a Small Major Seventh is interesting and at odds with Smith's interval names. Given that 9:5 is larger than 16:9, and no Minor Seventh is mentioned, we can assume 16:9 was mislabeled as a Major Seventh and was understood to be a Minor Seventh, as referred to by Smith.
There is an inconsistency associated with the labeling of 9:5 as a Small Major Seventh also, as it lies a 3:2 Fifth above the 6:5 Minor Third, and we know a fifth and a minor third when added together to give a minor, rather than major seventh.
Ellis here uses the name for 8:7 we suggested above, Super-major Second, and includes our suggested Sub-minor Sixth and Super-major Sixth, however rather than Subminor Fifth and Supermajor Fourth, 7:5 and 10:7 are labelled Sub-Fifth and Super-Fourth, where in this instance sub and super are seen to raise and lower by 21:20 instead of by 36:35.
Ellis, in a footnote to his translation of Helmholtz,'s treatise also provides names for a single 11-limit interval. The interval 22:27, of 355c, introduced by Zalzal, says Ellis was termed a neutral Third by Herr J. P. N. Land originally in Over de Toonladders der Arabische Musiek (On the Scales of Arabic Music) in 1880. An interval a fourth higher than this is mentioned, but a ratio is not given, and it is not named. We can ourselves however find it's ratio as 11:18, and guess it's name to be a neutral Sixth, given that it lies a perfect Fourth above the neutral Third. Following a similar process as in our completion of Helmholtz table above, and assuming that the octave inverse of a neutral Third should be a neutral Sixth we may introduce the following 11-limit intervals that see common use among music theorists and microtonal musicians through to today:
| Intervals | Notation | Ratio | Cents in the interval |
|---|---|---|---|
| Neutral Second | D♭^ | 81:88 | 143 |
| Neutral Second | Dv | 11:12 | 151 |
| Neutral Third | E♭^ | 9:11 | 347 |
| Neutral Third | Ev | 22:27 | 355 |
| Neutral Sixth | A♭^ | 27:44 | 845 |
| Neutral Sixth | Av | 11:18 | 853 |
| Neutral Seventh | B♭^ | 6:11 | 1049 |
| Neutral Seventh | Bv | 44:81 | 1057 |
Each interval name has two sizes that differ by the comma 243/242. The notation included in the table is from HEWM notation, developed as an extension to the Helmholtz-Ellis use of '+' and '-' by Joseph Monzo (http://www.tonalsoft.com/enc/h/hewm.aspx).'^' indicates raising 'v' a lowered of 33/32. In HEWM notation '+' and '-' are refined to mean raising and lowering of 81/80 respectively and '>' and '<' are added instead to indicate raising and lowering of 64/63. Letter names correspond instead of the Ptolemaic sequence, as in Smith's and Helmholtz' descriptions, but to a Pythagorean tuning of the diatonic scale, where '#' and '♭' and respectively raise and lower the apotome, 2187/2048. HEWM notation is not accompanied by an interval naming system.
Common interval names today
These interval names are used by theorists and microtonal musicians today, though 7/5 and 10/7 are given many different names, today also considered to be an augmented fourth and diminished fifth, lesser septimal tritone and greater septimal tritone, or simply as tritones. The fourth and fifth are today called perfect fourth and perfect fifth, and Smith's major Fourth and minor Fifth referred to as augmented fourth and diminished fifth respectively. As can be seen in Tchaikovsky's A Guide to the Practical Study of Harmony, by the beginning of end of the 19th century the familiar conventions for the naming of intervals were set, wherein
- Seconds, thirds, sixths and sevenths appear in the diatonic in two sizes, the larger labelled 'major' and the smaller, 'minor'.
- Major, when raised by a semitone, becomes 'augmented', and minor, lowered by a semitone, 'diminished'.
- The smaller of the two sizes of fourth and the larger of the two sizes of fifth are labelled 'perfect', along with the unison and octave.
- A perfect interval, when raised a semitone is labelled 'augmented', and when lowered a semitone, 'diminished'.
Fokker/Keenan extended-diatonic interval-names
Considering the 11-limit otonal chord 4:5:6:7:9:11 a chain of thirds, in addition to the familiar major, minor, subminor, supermajor and neutral thirds, Dave Kennan labelled 5:7 a sub-diminished fifth and 7:11 an augmented fifth. 7:10, the inversion of 5:7, is labelled a diminished. 5:7, therefore, is also an augmented fourth. In terms of sevenths, 4:7 is subminor, 5:9 is minor and 11:6 is neutral.
From this, Keenan defines a consistent interval naming system, meaning one which obeys diatonic interval arithmetic (In each column, the parenthesised prefix is the one that is implied when there is no prefix). When adding intervals the indexes are added together to give the index of the resulting interval. Keenan also adds corrections for each interval class to the indexes in order to account for inconsistencies that occur within diatonic interval arithmetic when concerning intervals greater than an octave, so that his system, unlike regular diatonic interval names, may be completely consistent.
As can be seen above, sub, super, augmented and diminished have also carried inconsistent meaning historically, where in Keenan's system they always alter intervals by the same amount.
| Index | Prefix for unisons, fourths, fifths, octaves | Prefix for seconds, thirds, sixths, sevenths, ninths |
|---|---|---|
| -4 | double diminished | subdiminished |
| -3 | subdiminished | diminished |
| -2 | diminished | subminor |
| -1 | sub | minor |
| 0 | (perfect) | neutral |
| 1 | super | (major) |
| 2 | augmented | supermajor |
| 3 | superaugmented | augmented |
| 4 | double augmented | superaugmented |
The index values correspond most directly to degrees of 31-tET, whose interval names by this method are given in the following table:
| 31-tET degree | Ratios | Names | |
|---|---|---|---|
| 0 | 1:1 | unison | |
| 1 | 48:49 44:45 36:35 33:32 | (diminished second) | super unison |
| 2 | 27:28 24:25 20:21 | subminor second | (augmented unison) |
| 3 | 15:16 14:15 | minor second | |
| 4 | 11:12 10:11 | neutral second | |
| 5 | 9:10 8:9 | major second | |
| 6 | 7:8 | supermajor second | (diminished third) |
| 7 | 6:7 | (augmented second) | subminor third |
| 8 | 5:6 | minor third | |
| 9 | 9:11 | neutral third | |
| 10 | 4:5 | (subdiminished fourth) | major third |
| 11 | 11:14 7:9 | (diminished fourth) | supermajor third |
| 12 | 16:21 | subfourth | (augmented third) |
| 13 | 3:4 | perfect fourth | |
| 14 | 8:11 | super fourth | |
| 15 | 5:7 | augmented fourth | (subdiminished fifth) |
| 16 | 7:10 | (superaugmented fourth) | diminished fifth |
| 17 | 11:16 | sub fifth | |
| 18 | 2:3 | perfect fifth | |
| 19 | 21:32 | (diminished sixth) | super fifth |
| 20 | 9:14 7:11 | subminor sixth | (augmented fifth) |
| 21 | 5:8 | minor sixth | (superaugmented fifth) |
| 22 | 11:18 | neutral sixth | |
| 23 | 3:5 | major sixth | |
| 24 | 7:12 | supermajor sixth | (diminished seventh) |
| 25 | 4:7 | (augmented sixth) | subminor seventh |
| 26 | 9:16 5:9 | minor seventh | |
| 27 | 11:20 6:11 | neutral seventh | |
| 28 | 8:15 | major seventh | |
| 29 | 14:27 | (diminished octave) | supermajor seventh |
| 30 | 18:35 | sub octave | (augmented seventh) |
| 31 | 1:2 | octave |
The interval names shown in brackets could be said to be 'secondary', the others, 'primary'.
After releasing his system Keenan was informed that is was identical to the extended-diatonic interval-naming scheme of Adriaan Fokker but for the acknowledgment of more 11-limit ratios.This system depends on the tempering out of 81/80, where the diatonic major third, from four stacked fifths, approximates the just major third, 5/4. It also depends on the existence of neutral intervals, i.e., that the perfect fifth or equivalently, the chromatic semitone, subtends an even number of degrees of the ET. To simply to our familiar naming scheme for 12-tET, we observe that it applies to 24-tET equally as directly as in 31-tET, where the prefixes correspond to degrees of the ET. Exactly the same is also true for 38-tET, twice 19-tET, a meantone which very closely approximates 1/3-comma Meantone. Meantone temperament wherein the fifth is divided into two equally sized neutral thirds is referred to as neutral temperament. Whereas meantone temperament is generated by the fifth, in neutral temperament the generator is half this interval, the neutral third. Where it was seen above that there are two neutral thirds, 9:11 and 22:27 that differ by 243/242, neutral temperament is at its most simple the temperament defined by this equivalence: the tempering out of 243/242, as meantone is defined by the tempering out of 81/80. The temperament that tempers out both 81/80 and 243/242 is called Mohajira, upon which Keenan's scheme can be said to be based. As well as 24-tET, 31-tET and 38-tET, Mohajira is supported by 7-tET and 17-tET.
The primary interval names resulting in this system's application to these ETs is now show for easy comparison, where 'M', 'm', 'P', 'N', 'A', 'd', 'S' and 's' are shorthand for major, minor, perfect, neutral, augmented, diminished, super and sub, respectively:
7-tET: P1 N2 N3 P4 P5 N6 N7 P8
17-tET: P1 m2 N2 M2 m3 N3 M3 P4 S4 s5 P5 m6 N6 M6 m7 N7 M7 P8
24-tET: P1 S1/sm2 m2 N2 M2 SM2/sm3 m3 N3 M3 SM3/s4 P4 S4 A4/d5 s5 P5 S5/sm6 m6 N6 M6 SM6/sm7 m7 N7 M7 SM7/s8 P8
31-tET: P1 S1 sm2 m2 N2 M2 SM2 sm3 m3 N3 M3 SM3 s4 P4 S4 A4 d5 s5 P5 S5 sm6 m6 N6 M6 SM6 sm7 m7 N7 M7 SM7 s8 P8
38-tET: P1 S1 A1 sm2 m2 N2 M2 SM2 A2/d3 sm3 m3 N3 M3 SM3 d4 s4 P4 S4 A4 SA4/sd5 d5 s5 P5 S5 A5 sm6 m6 N6 M6 SM6 A6/d7 sm7 m7 N7 M7 SM7 d8 s8 P8
to Meantone tunings that are not Mohajira tunings, the regular diatonic interval names can be applied, but with the addition of double augmented and double diminished from Fokker/Keenan's system.
19-tET: P1 A1 m2 M2 A2/d3 m3 M3 d4 P4 A4 d5 P5 A5 m6 M6 A6/d7 m7 d8 P8 (every second step of 38edo)
26-tET: P1 A2 d2 m2 M2 A2 d3 m3 M3 A3 d4 P4 A4 AA4/AA5 d5 P5 A5 d6 m6 M6 A6 d7 m7 M7 A7 d8 P8
In the above primary interval names for equal tunings, it should be noted that no interval of interval-class n-1 is subtended by a larger number of degrees than an interval of class n. I define that an interval-name set for which this is true is said to be well-ordered. The possibility for well-ordered interval-name sets is a desirable property for interval naming schemes to possess and is possess by all proposals discussed in this paper.
Keenan adds further that if it is desired to distinguish between ratios that are in 31-tET approximated by the same number of steps, an addition prefix be added to describe the prime limit of the approximated interval. For 3-limit intervals, the obvious choice is 'Pythagorean', for 5-limit Keenan chooses 'classic', for 7, 'septimal, 11, 'undecimal' and 13, 'tridecimal'. When the highest prime is the same, Keenan suggests adding 'small' and 'large' as final prefixes for this purpose.
The modern interval names were built on the assumption of meantone tempering, where the major third built from four fifths is the approximation of 5/4. In non-Meantone tunings, these two definitions of major third, just (or classic) and Pythagorean major thirds no longer correspond. If intervals are to receive unique names then to one or both of these major thirds must be added a prefix. A prefix to a major third might suggest it is not considered the 'true' major third. Keenan has been involved with the development of both types of systems. Only when the major is defined by its mapping as fourth fifths, i.e. 81/64, can conserve interval arithmetic, but that may lead to a scheme that goes against what people believe the intervals to sound like.
Miracle interval naming
Keenan later describes how the scheme can be extended to also cover 72-tET and 41-tET. In 31-tET the fifth may divided into six minor seconds. This temperament is called Miracle, and is also supported by 41-tET and 72-tET. The first six generators of Miracle give the following intervals: P1 m2 SM2 m3 S4 P5, as can be seen in the table above. 31-tET may be covered by 15 generators downwards and 15 generators upwards from 1:1. In 72-tET, either side of the intervals that that result from these 31 notes, called Miracle[31] 15|15, lie unnamed intervals that may be found first at either 31 or 41 generators further upwards or downwards and in 41-tET, either at 10 or 31 generators. If, one degree of 41 or 72-tET above an interval or Miracle[31] 15|15 lies an unnamed interval that can be first found by an additional 31 generators upwards, it is given the same name as the interval directly below it, with the addition of the prefix 'n', for 'narrow'. Similarly, 'W' for 'wide' prefixes an unnamed interval one degree, 31 generators below.
41-tET: P1 S1 nsm2 sm2 m2 N2 nM2 M2 SM2 sm3 nm3 m3 N3 M3 nSM3 SM3 s4 P4 nS4 S4 A4 d5 s5 Ws5 P5 S5 sm6 Wsm6 m6 N6 M6 Wm6 SM6 sm7 m7 Wm7 N7 M7 SM7 WSM7 s8 P8
In 41-tET, fourth fifths make a wide major third, rather than a major third, and interval arithmetic is no longer conserved. The same is true for 72-tET, so we are still yet to find a scheme able to conserve interval arithmetic in non-meantone ETs. Though many edos can be covered, many still cannot, including the Superpythagorean edos, where the fifth is sharper than just, and four fifths give an approximation to 7:9, the super major third, tempering out the septimal comma, 63:64.
Sagittal and sagispeak
Sagispeak, one system which in its naming of meantone and non-meantone edos is able to conserve interval arithmetic was developed initially by George Secor as a way to pronounce accidentals used in Saggital notation, a generalised diatonic-based notation system applicable equally to just intonation, equal tunings and rank-n temperaments. With input from Dave Keenan and others, Cam Taylor extended it for use as an interval naming system. In Saggital, dozens of different accidentals can be used on a regular diatonic staff to notate up to extremely fine divisions, however in most cases only a handful are needed. In Sagispeak, each accidental is presented by a prefix, made up of a single letter, in most cases, followed by either 'ai' if the accidental raises a note, or 'ao' if it lowers a note. As in HEWM notation, Pythagorean intonation is assumed as a basis. Then prefixes depart from Pythaogrean intonation, altering by commas and introducing other primes. In place of the prefixes 'sub' and 'super', generally signifying an alteration of 36/35 from 5-limit intervals or 64/63 from 3-limit, Sagittal features an accidental of 64/63, which may be used to take a Pythagorean major interval to a supermajor, minor to subminor, or perfect to super or sub. The prefix 'tao' indicates a decrease of 64/63 and the prefix 'tai' an increase. Whereas in previous interval naming schemes 'major' and 'minor' were synonymous with the 5-limit tunings, in Sagispeak they map instead to Pythagorean. A prefix is needed then to take a Pythagorean intoned interval to a 5-limit tuning. Where 5/4 is 81/80 below the Pythagorean third, the prefixes 'pai' and 'pao' (where 'p' is for 'pental', as in, involving prime 5), which raise or lower a note by 81/80 respectively. Similarly, 'vai' and 'vao', which raise or lower a note by 33/32 respectively, leading to ratios of 11.
Because it is built off of the diatonic scale, Sagispeak conserves diatonic interval arithmetic, i.e. familiar relations in the diatonic scale, i.e. M2 + m3 = P4. As in Fokker/Keenan Extended-diatonic Interval-names, diatonic interval arithmetic is also extended, where, for example, tai-major 2 + tao-minor 3 = P4 (8/7 + 7/6 = 4/3), where opposite alterations cancel each other out, and diatonic interval arithmetic is conserved, a very useful property for a microtonal interval naming system to possess. Another helpful property of Sagispeak is its generalised applicability to edos, just intonation and other tunings, where the same intervals maintain their spelling across different tunings. Despite these benefits however, many see Sagittal and Sagispeak as overly complex (even though the entire extended system need hardly ever be applied), and requiring too many new terms to be learnt. It is also worth noting that since 5/4 is in his system referred to as a pao-M3, and the major third, in systems with sharper fifth particularly, may be fairly sharp of this familiar tuning for a major third, intervals names may no longer correspond to what they 'sound like'. In superpythagorean systems, for example, the major third approximates 9/7, which is familiar from meantone-based naming as a super major third. This is true of any scheme in which the major third is defined by its generation from fifths. On the other hand, any scheme in which the major third is defined instead as an approximation to 5/4 does not preserve interval arithmetic in non-meantone systems, but may conserve existing associations between interval names and sound / size.
For comparison, 31-tET, is shown below in sagispeak:
31-tET: P1 tai-1/vai-1 tao-m2 m2 vai-m2/vao-M2 M2 tai-M2 tao-m3 m3 vai-m3/vao-M3 M3 tai-M3 tao-4 P4 vai-4 A4 d5 vao-5 P5 tai-5 tao-m6 m6 vai-m6/vao-M6 M6 tai-M6 tao-m7 m7 vai-m7.vao-M7 M7 tai-M7 vao-8/tao-8 P8
Dave Keenan's most recent system

In 2016 Dave Keenan proposed an alternative generalised microtonal interval naming system for edos. In what might be understood as a generalisation of his extended-diatonic interval-naming system described above onto any equal tuning. Employing as prefixes the familiar 'sub', 'super', and 'neutral'. His scheme is based on the diatonic scale, however the diatonic interval names are not defined by their position in a cycle of fifths like is Sagispeak. In Keenan's system the ET's best 3/2 is first labelled P5, and the fourth P4. The interval half-way between the tonic and fifth is labelled the neutral third, or 'N3', and halfway between the fourth and the octave N6. Then the interval a perfect fifth larger than N3 is labelled N7, and the interval a fifth smaller than N6 labelled N2. The neutral intervals then lie either at a step of the ET, or between two steps. After this the remaining interval names are decided based on the distance they lie in pitch from the 7 labelled intervals, which make up the Neutral scale, P1 N2 N3 P4 P5 N6 N7, which, like the diatonic, is an MOS scale, which may be labelled Neutral[7] 3|3 using Modal UDP notation. This results in the conservation of symmetry about the tetrachord and the octave, and the symmetry of 3rds in a fifth. The interval arithmetic associated with these symmetries which may be summarised by the rule 'x + y = Pz and x + Pz = y where x and y are both perfect, both major/minor, or both dim/aug', is also conserved. To name an interval in an ET, the number of steps of 72-tET that most closely approximate the size of the interval difference from a note of the neutral scale is first found. Then the prefix corresponding to that number of steps of 72-tET is applied to the interval name. The diagram to the right details this process. An interval just smaller than a major third in Keenan's system is labelled a narrow major third, and an interval just wider than a 6/5 minor third a wide minor third, however he notes that 'narrow' and 'wide' are only necessary in edos greater than 31. This system is equivalent to the Fokker/Keenan Extended-diatonic interval-naming system and Miracle interval naming when applied to any of the ETs they were able to cover. In application to ETs whose best fifth lies outside of the regular diatonic range (between 4 degrees of 7-tET, and 3 degrees of 5-tET)
Keenan's system is an elegant way to keep the 'major 3rd' label for 5/4 in application to non-meantone edos, while conserving interval arithmetic that results from symmetry about the tetrachord and the octave. However, much interval arithmetic remains unconserved in non-meantone ETs. A potentially undesirable result of the system is that the major second approximates 10/9, and a wide major second 9/8, where as 9/8 is almost always considered a major second, and 10/9 often a narrow or small major second. One such system that considers 10/9 a narrow major second is that of Aaron Hunt.
Size-based systems
Microtonal theorist Aaron Andrew Hunt devised the Hunt system, which includes interval name assignments for JI (just intonation) and edos based on 41edo. Compared to Keenan's 72 interval names, Aaron's system includes 41. His system is based directly on 41-tET, and unlike Keenan's system, interval are given the name of the closest step of 41-tET, and no account is taken of the size of the edos fifth. In 41-tET, Major, minor, augmented and diminished intervals are those obtained through the approximately Pythagorean cycle of fifths. Intervals one step of 41-tET above these are given the prefix 'small', one step larger are given the prefix 'large', two steps smaller the prefix 'narrow' and two larger the prefix 'wide'. As a result, 5/4 is labelled a 'small major 3rd', or SM3 (not to be confused with a super major third, a label that does not exist in this system).
Neo-medieval musician and early music historian and theorist Margo Schulter described her own interval naming scheme built on approximations to JI intervals. Each interval names corresponds to an approximate size, and no particular ET is referenced. In her scheme middle major thirds range in size from 400-423 cents, and small major thirds from 372-400c. 5/4 is labelled a small major third, 81/64 a middle major third and 9/7 a large major third. Margo's scheme includes small, middle and large varieties of major, minor and neutral 2nds, 3rds, 6ths, 7ths; perfect fourth and fifths; and tritones, as well as a sub fifth and super fourth; a dieses and comma and an octave less dieses and comma; and interseptimals, which correspond to intermediates, her name referencing the fact that they may each approximate two ratios of 7.
In Hunt's system when used in 41-tET or JI diatonic interval arithmetic is conserved, but in other tunings it may not be, and Margo's system may not conserve diatonic interval arithmetic either. Both systems may be applied to arbitrary tunings, but the same intervals (defined, perhaps by a MOS scale) may not be given the same interval names across different tunings. Other size-based systems also exist, but are less thoroughly described and less well known. In all these systems, interval arithmetic is not conserved across all tunings.
Ups and Downs
One final interval naming system, associated with the Ups and downs notation system, belonging to microtonal theorist and musician Kite Giedraitis, like Sagittal is based on deviations from pythagorean intervals. In this system however, deviations (from major, minor, perfect, augmented and diminished) are notated simply by the addition of up or down arrows: '^' or 'v', corresponding to raising or lowering of a single step of an edo. In some tunings (12-tET, 19-tET or 31-tET for example) 5/4 may be a M3, and in others a vM3 (downmajor 3rd) (e.g. 15-tET, 22-tET, 41-tET, 72-tET), or even an up-major 3rd (e.g. 21-tET). Ups and downs also includes neutrals, which lay exactly in-between major and minor intervals of the same degree, labelled '~' (mid). The mid-4th ~4 is halfway between P4 and A4, and ~5 is likewise half-way diminished. 'Up' and 'down' prefixes may be used before mid also, e.g. 'v~ 3' in 72-tET. P1, P4, P5 and P8 when upped or downed (or midded, in the case of P4 and P5) are simply labelled '1', '4', '5' and '8'. This system benefits from its simplicity as well as its conservation of interval arithmetic. The latter makes possible the naming of chords, e.g. downminor 7th. Rank-2 temperaments may also be described, with the possible addition of an additional pair of qualifiers, lifts and drops - '/' and '\'. A rank-2 scale, such as a MOS scale may appear different than this rank-2 notation when approximated in an equal (rank-1) tuning. Another criticism of Kite's system that does not apply to the others is the fact that when an edo is doubled or multiplied by some simple fraction, and the best fifth is constant across the two edos, the same intervals may be given different names.
Igliashon Jones is a supporter of this system, but for the relabeling of 'down' as 'sub' and 'up' as 'super' and 'mid' as 'neutral', so that more common names are used, wherein 'super' infers a raise of 1 step of the edo, and 'sub' a lowering of one step. In this 'Extra-diatonic' system 'super' and 'sub' may be doubly applied, as in Ups and Downs, but they may not be applied before 'neutral' where in Ups and Downs they may be applied before 'mid'.
31-tET in Ups and Downs:
P1 ^1 A1/vm2 m2 ~2 M2 ^M2 vm3 m3 ~3 M3 ^M3 v4 P4 ^4 A4 d5 v5 P5 ^5 A5/vm6 m6 ~6 M6 ^M6 vm7 m7 ~7 M7 ^M7 v8 P8
In Jones' relabeling 31edo appears as in Fokker/Keenan Extended-diatonic Interval-names.
FKH Extended-diatonic interval names
This review was both motivated by, and has been integral to, the development of the author's own interval naming scheme. FKH (Fokker/Keenan/Hearne) Extended-diatonic interval names, are essentially an extension of Fokker/Keenan Extended-diatonic interval-names (with a nod to Smith, Helmholtz and Ellis), redesigned with Pythagorean intonation at the core, from Sagittal/Sagispeak, where prefixes correspond to alteration by specific commas, into non-meantone edos, keeping interval arithmetic conserved. 'S' and 's', for 'super' and 'sub' suggest alteration by 64/63, and for seconds, thirds, sixths and sevenths, sub and super intervals remain the same as they have been since Helmholtz/Ellis. Similarly, 'C' and 'c' suggest alteration by 81/80. For perfect intervals 'C' and 'c' are short for 'comma-wide' and 'comma-narrow' respectively, derivative of part of Smith's interval naming scheme, and for all other intervals they are short for 'classic', after Keenan's use of the word. In this way the 5/4 major third in non-meantone system receives a label that is still suggestive of it being a familiar major third.
As in Keenan/Fokker Extended-diatonic interval-names, N lies exactly between M and m, splitting the apotome. 'hA' and 'hd' for 'hemi-augmented' and 'hemi-diminished' are added for similar use from perfect intervals as N from major and minor, e.g. in 31-tET 11/8 is labelled hA4 rather than S4, and 33/32 hA1 rather than S1. 'Intermediates' are also included when the limma, is split, rather than the apotome. Where neutrals are associated with the tempering out of 243/242, intermediates are associated with the tempering out of 676/675, where 13/15 is equated with half of 4/3, labeled '2-3'. Finally, 'wide' and 'narrow', with short-form 'W' and 'n' fill the role of ups and downs from Ups and Downs, and a similar role to their namesake in Fokker/Keenan Extended-interval names. This scheme conserves interval arithmetic wherever it may be applied, which is to all edos and many, but not all MOS and JI scales, where names for the intervals of scales are conserved across different tunings.
In addition to the 'primary names' seen below, secondary names can be included which may reveal commas tempered out, and in turn what the diatonic intervals 'sound like', as well as the correspondence between chromatic and enharmonic movement and commatic movement. For example, in 22-tet, listed below, the secondary names for the diatonic intervals show 'S' and 's' subscripts, suggesting the tempering out of 64/63 and providing the information that in 22-tET the 'structural' major third is also, or 'sound like' a super major third, for example. The classic major third is secondarily named as an augmented second, so we know how to chromatically 'find it' / how it derives from the diatonic scale. These equivalences define 7-limit Superpyth temperament.
16-tET, 22-tET, 41-tET and 50-tET are given below as examples:
16-tET: P1 S1 Cm2 cM2 Cm3 cM3 s4 P4 S4/s5 P5 S5 Cm6 cM6 Cm7 cM7 s8 P8
22-tET: P1 m2 Cm2 cM2 M2 m3 Cm3 cM3 M3 P4 C4 cA4/Cd5 c5 P5 m6 Cm6 cM6 M6 m7 Cm7 cM7 M7 P8
41-tET: P1 C1/S1 sm2 m2 Cm2 N2 cM2 M2 SM2 sm3 m3 Cm3 N3 cM3 M3 SM3 s4 P4 C4 hA4 cA4 Cd5 hd5 c5 P5 S5 sm6 m6 Cm6 N6 cM6 M6 SM6 sm7 m7 Cm7 N7 cM7 M7 SM7 c8/s8 P8
53-tET: P1 C1/S1 1-2 sm2 m2 Cm2 SCm2 scM2 sM2 M2 SM2 2-3 sm3 m3 Cm3 SCm3 scM3 cM3 M3 SM3 3-4 s4 P4 C4 SC4 scA4 cA4 Cd5 SCd5 SA4/sc5 c5 P5 S5 5-6 sm6 m6 Cm6 SCm6 scM6 sM6 M6 SM6 6-7 sm7 m7 Cm7 SCm7 scM7 cM7 M7 SM7 7-8 c8/s8 P8