7edo
| ← 6edo | 7edo | 8edo → |
(semiconvergent)
7 equal divisions of the octave (abbreviated 7edo or 7ed2), also called 7-tone equal temperament (7tet) or 7 equal temperament (7et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 7 equal parts of about 171 ¢ each. Each step represents a frequency ratio of 21/7, or the 7th root of 2.
Theory
7edo is the basic example of an equiheptatonic scale, and in terms of tunings with perfect fifths, is essentially the next size up from 5edo. The 7-form is notable as a common structure for many 5-limit systems, including all seven modes of the diatonic scale—Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian; in 7edo itself, the two sizes of interval in any heptatonic MOS scale are equated, resulting in a neutral feel. All triads are neutral (except if you use suspended triads, which are particularly harsh in 7edo due to the narrowed major second), so functional harmony is almost entirely based on the positions of the chords in the 7edo scale.
The second (171.429 ¢) works well as a basic step for melodic progression. The step from seventh to octave is too large as a leading tone - possibly lending itself to a "sevenplus" scale similar to elevenplus.
In terms of just intonation, the 3/2 is flat but usable, but we don't find particularly accurate intervals in pure harmonics outside the 3-limit, which suggests a more melodic approach to just intonation; intervals approximated by each of 7edo's steps include 10/9 for 1 step, 11/9 for 2 steps, 4/3 for 3 steps, and their octave complements. Interestingly, this renders an 8:9:10:11:12 pentad equidistant, from which it can be derived that 7edo supports meantone (equating the major seconds 10/9 and 9/8) and porcupine (splitting 4/3 into three equal submajor seconds which simultaneously represent 12/11, 11/10, and 10/9), and is the unique system to do so.
Due to 7edo's inaccurately tuned 5/4 major third (which is flat by over 40 cents), it supports several exotemperaments in the 5-limit, such as dicot (which splits the fifth into two equal neutral thirds, simultaneously representing 5/4 and the minor third 6/5) and mavila (which flattens the fifth so that the diatonic "major third" actually approximates 6/5); 6/5 is a slightly more reasonable interpretation of 7edo's third than 5/4, leading to an overall slightly minor sound.
In higher limits, this third takes on a new role: as a neutral third, it is a decent approximation of the 13th subharmonic, and as such 7edo can be seen as a 2.3.13 temperament. This third is a near perfect approximation of the interval 39/32; the equation of 16/13 and 39/32 is called harmoneutral temperament. In general, the inclusion of 13 allows the pentad discussed earlier to be continued to an 8:9:10:11:12:13 hexad, although the specific interval 13/12 is inaccurate due to the errors adding up in the same direction.
The seventh of 7edo is almost exactly the 29th harmonic (29/16), which can have a very agreeable sound with harmonic timbres. However it also finds itself nested between ratios such as 20/11 and 9/5, which gives it considerably higher harmonic entropy than 7/4, a much simpler overtone seventh.
7edo represents a 7-step closed circle of fifths, tempering out the Pythagorean chromatic semitone. However, it can also be seen as a circle of neutral thirds, which can be interpreted as 11/9; this is called neutron temperament.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -16.2 | -43.5 | +59.7 | -37.0 | +16.6 | +66.5 | +45.3 | +57.4 | -1.0 | +55.0 |
| Relative (%) | +0.0 | -9.5 | -25.3 | +34.9 | -21.6 | +9.7 | +38.8 | +26.5 | +33.5 | -0.6 | +32.1 | |
| Steps (reduced) |
7 (0) |
11 (4) |
16 (2) |
20 (6) |
24 (3) |
26 (5) |
29 (1) |
30 (2) |
32 (4) |
34 (6) |
35 (0) | |
In non-Western traditions
Equiheptatonic scales close to 7edo are used in non-western music in some African cultures[1] as well as an integral part of early Chinese music[2]. Also Georgian music seems to be based on near-equal 7-step scales.
It has been speculated in Indian music: history and structure[3] that the Indian three-sruti interval of 165 cents is very similar to one 171-cent step of 7edo.
In equiheptatonic systems the desire for harmonic sound may dictate constant adjustments of intonation away from the theoretical interval of 171 cents. (Similar to adaptive just intonation but with equal tuning instead).
One region of Africa in which a pen-equidistant heptatonic scale is combined with a distinctively harmonic style based on singing in intervals of thirds plus fifths, or thirds plus fourths, is the eastern Angolan area. This music is heptatonic and non-modal; i.e., there is no concept of major or minor thirds as distinctive intervals. In principle all the thirds are neutral, but in practice the thirds rendered by the singers often approximate natural major thirds (5/4, 386 ¢), especially at points of rest. In this manner, the principles of equidistance and harmonic euphony are accommodated within one tonal-harmonic system.
A Ugandan, Chopi xylophone measured by Haddon (1952) was also tuned something close to this.
It has often been stated that 7edo approximates tunings used in Thai classical music, though this is a myth unsupported by empirical studies of the instruments.[4]
Subsets and supersets
7edo is the 4th prime edo, after 5edo and before 11edo. It does not contain any nontrivial subset edos, though it contains 7ed4. Multiples such as 14edo, 21edo, … up to 35edo, share the same tuning of the perfect fifth as 7edo, while improving on other intervals.
Intervals
| Degree | Cents | Interval region | Approximated JI intervals (error in ¢) | Audio | |||
|---|---|---|---|---|---|---|---|
| 3-limit | 5-limit | 7-limit | Other | ||||
| 0 | 0 | Unison (prime) | 1/1 (just) | ||||
| 1 | 171.429 | Submajor second | 10/9 (-10.975) | 54/49 (+3.215) | 11/10 (+6.424) 32/29 (-1.006) |
||
| 2 | 342.857 | Neutral third | 128/105 (+0.048) | 39/32 (+0.374) 16/13 (-16.6) 11/9 (-4.551) |
|||
| 3 | 514.286 | Fourth | 4/3 (+16.241) | 27/20 (-5.265) | 35/26 (-0.326) | ||
| 4 | 685.714 | Fifth | 3/2 (-16.241) | 40/27 (+5.265) | 52/35 (+0.326) | ||
| 5 | 857.143 | Neutral sixth | 105/64 (-0.048) | 18/11 (+4.551) 13/8 (+16.6) 64/39 (-0.374) |
|||
| 6 | 1028.571 | Supraminor seventh | 9/5 (+10.975) | 49/27 (-3.215) | 29/16 (-1.006) 20/11 (-6.424) |
||
| 7 | 1200 | Octave | 2/1 (just) | ||||
Notation
The usual notation system for 7edo is the chain-of-fifths notation, which is directly derived from the standard notation used in 12edo.
Because the Pythagorean apotome (2187/2048) is tempered out, sharps (♯) and flats (♭) are redundant in 7edo. Therefore, 7edo can be notated on a five-line staff without accidentals. Alternatively, a seven-line stave can be used, with each horizontal line representing one pitch level. There is no distinction between major or minor, so every interval has the interval quality "perfect" instead.
| Degree | Cents | Chain-of-fifths notation | |
|---|---|---|---|
| Diatonic interval names | Note names (on D) | ||
| 0 | 0 | Perfect unison (P1) | D |
| 1 | 171.429 | Perfect second (P2) | E |
| 2 | 342.857 | Perfect third (P3) | F |
| 3 | 514.286 | Perfect fourth (P4) | G |
| 4 | 685.714 | Perfect fifth (P5) | A |
| 5 | 857.143 | Perfect sixth (P6) | B |
| 6 | 1028.571 | Perfect seventh (P7) | C |
| 7 | 1200 | Perfect octave (P8) | D |
In 7edo:
- Ups and downs notation is identical to circle-of-fifths notation;
- Mixed and pure sagittal notation are identical to circle-of-fifths notation.
Sagittal notation
This notation is a subset of the notations for EDOs 14, 21, 28, 35, and 42b.
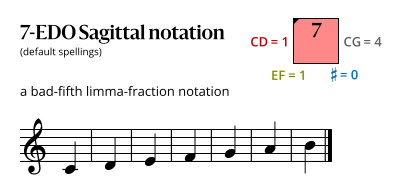
Because it includes no Sagittal symbols, this Sagittal notation is also a conventional notation.
Alternative notations
William Lynch proposes using numbers 1 through 7 as the nominals of 7edo with sharp signs being possible to expand to 14edo or even 21edo.
Solfege
| Degree | Cents | Standard solfege (movable do) |
Uniform solfege (1 vowel) |
|---|---|---|---|
| 0 | 0 | Do | Da |
| 1 | 171.429 | Re | Ra |
| 2 | 342.857 | Mi | Ma |
| 3 | 514.286 | Fa | Fa |
| 4 | 685.714 | So | Sa |
| 5 | 857.143 | La | La |
| 6 | 1028.571 | Ti | Ta |
| 7 | 1200 | Do | Da |
Approximation to JI
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 6.7930 | 6.8911 | 7df | ⟨7 11 16 19 24 25] |
| 6.8911 | 6.9460 | 7d | ⟨7 11 16 19 24 26] |
| 6.9460 | 7.0821 | 7 | ⟨7 11 16 20 24 26] |
| 7.0821 | 7.1062 | 7e | ⟨7 11 16 20 25 26] |
| 7.1062 | 7.1613 | 7ce | ⟨7 11 17 20 25 26] |
| 7.1613 | 7.2557 | 7ceff | ⟨7 11 17 20 25 27] |
Commas
7et tempers out the following commas. This assumes val ⟨7 11 16 20 24 26].
| Prime limit |
Ratio[note 1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 2187/2048 | [-11 7⟩ | 113.69 | Lawa | Whitewood comma, apotome, Pythagorean chroma |
| 5 | 135/128 | [-7 3 1⟩ | 92.18 | Layobi | Mavila comma, major chroma |
| 5 | 25/24 | [-3 -1 2⟩ | 70.67 | Yoyo | Dicot comma, classic chroma |
| 5 | 250/243 | [1 -5 3⟩ | 49.17 | Triyo | Porcupine comma, maximal diesis |
| 5 | 20000/19683 | [5 -9 4⟩ | 27.66 | Saquadyo | Tetracot comma, minimal diesis |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic comma, Didymus' comma, meantone comma |
| 5 | (14 digits) | [9 -13 5⟩ | 6.15 | Saquinyo | Amity comma |
| 7 | (14 digits) | [9 7 -5 -3⟩ | 75.64 | Triru-aquingu | Superpine comma |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Mint comma, septimal quartertone |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's enharmonic diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | 875/864 | [-5 -3 3 1⟩ | 21.90 | Zotriyo | Keema |
| 7 | 5120/5103 | [10 -6 1 -1⟩ | 5.76 | Saruyo | Hemifamity comma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutriyo | Porwell comma |
| 7 | 4375/4374 | [-1 -7 4 1⟩ | 0.40 | Zoquadyo | Ragisma |
| 7 | (30 digits) | [47 -7 -7 -7⟩ | 0.34 | Trisa-rugu | Akjaysma |
| 11 | 33/32 | [-5 1 0 0 1⟩ | 53.27 | Ilo | Io comma, undecimal quartertone |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lurugugu | Valinorsma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.39 | Satrilu-aruru | Orgonisma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Triluyo | Wizardharry comma |
| 13 | 14641/13312 | [-10 0 0 0 4 -1⟩ | 164.74 | ||
| 13 | 52/49 | [2 0 0 -2 0 1⟩ | 102.87 | thoruru unison | Hammerisma |
| 13 | 27/26 | [-1 3 0 0 0 -1⟩ | 65.33 | Thu | Small tridecimal third tone |
| 13 | 65/64 | [-6 0 1 0 0 1⟩ | 26.84 | Wilsorma |
Temperaments
7edo is the first edo in which regular temperament theory starts to make sense as a way of subdividing the steps into mos scales, with three different ways of dividing it, although there is still quite a lot of ambiguity as each step can be considered as the sharp extreme of one temperament or the flat end of another.
1/7 can be considered the intersection of sharp porcupine and flat tetracot temperaments, as three steps makes a 4th and four a 5th. 2/7 can be interpreted as critically flat Mohajira or critically sharp amity, and creates mosses of 322 and 2221.
3/7 is on the intersection of meantone and mavila, and has MOS's of 331 and 21211, making 7edo the first edo with a non-equalized, non-1Lns pentatonic mos. This is in part because 7edo is close to low-complexity JI for its size, and is the second edo with a good fifth for its size (after 5edo), the fifth serving as a generator for the edo's meantone and mavila interpertations.
Octave stretch or compression
Stretched-octaves tunings such as 11edt, 18ed6 or 7ed257/128 greatly improves 7edo's approximation of harmonics 3, 5 and 11, at the cost of slightly worsening 2 and 7, and greatly worsening 13. If one is hoping to use 7edo for 11-limit harmonies, then these are good choices to make that easier.
- 7edo
- Step size: 171.429 ¢, octave size: 1200.000 ¢
Pure-octaves 7edo approximates the 2nd, 3rd, 11th and 13th harmonics well for its size, but it is arguable whether it approximates 5 – if it does it does so poorly. It does not approximate 7.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -16.2 | +0.0 | -43.5 | -16.2 | +59.7 | +0.0 | -32.5 | -43.5 | -37.0 | -16.2 |
| Relative (%) | +0.0 | -9.5 | +0.0 | -25.3 | -9.5 | +34.9 | +0.0 | -18.9 | -25.3 | -21.6 | -9.5 | |
| Steps (reduced) |
7 (0) |
11 (4) |
14 (0) |
16 (2) |
18 (4) |
20 (6) |
21 (0) |
22 (1) |
23 (2) |
24 (3) |
25 (4) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +16.6 | +59.7 | -59.7 | +0.0 | +66.5 | -32.5 | +45.3 | -43.5 | +43.5 | -37.0 | +57.4 | -16.2 |
| Relative (%) | +9.7 | +34.9 | -34.8 | +0.0 | +38.8 | -18.9 | +26.5 | -25.3 | +25.4 | -21.6 | +33.5 | -9.5 | |
| Steps (reduced) |
26 (5) |
27 (6) |
27 (6) |
28 (0) |
29 (1) |
29 (1) |
30 (2) |
30 (2) |
31 (3) |
31 (3) |
32 (4) |
32 (4) | |
- Step size: 171.993 ¢, octave size: 1203.948 ¢
Stretching the octave of 7edo by around 3.9 ¢ results in much improved primes 3, 5 and 11, but much worse primes 2, 7 and 13. The 2.3.11.13 WE tuning and 2.3.11.13 TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.9 | -10.0 | +7.9 | -34.4 | -6.1 | +71.0 | +11.8 | -20.1 | -30.5 | -23.5 | -2.1 |
| Relative (%) | +2.3 | -5.8 | +4.6 | -20.0 | -3.5 | +41.3 | +6.9 | -11.7 | -17.7 | -13.7 | -1.2 | |
| Step | 7 | 11 | 14 | 16 | 18 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +31.3 | +75.0 | -44.5 | +15.8 | +82.8 | -16.1 | +62.3 | -26.5 | +61.0 | -19.5 | +75.5 | +1.8 |
| Relative (%) | +18.2 | +43.6 | -25.9 | +9.2 | +48.2 | -9.4 | +36.2 | -15.4 | +35.5 | -11.4 | +43.9 | +1.1 | |
| Step | 26 | 27 | 27 | 28 | 29 | 29 | 30 | 30 | 31 | 31 | 32 | 32 | |
- Step size: 172.331 ¢, octave size: 1206.316 ¢
Stretching the octave of 7edo by around 6.3 ¢ results in much improved primes 3, 5 and 11, but much worse primes 2, 7 and 13. The tuning 18ed6 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +6.3 | -6.3 | +12.6 | -29.0 | +0.0 | +77.8 | +18.9 | -12.6 | -22.7 | -15.4 | +6.3 |
| Relative (%) | +3.7 | -3.7 | +7.3 | -16.8 | +0.0 | +45.1 | +11.0 | -7.3 | -13.2 | -8.9 | +3.7 | |
| Steps (reduced) |
7 (7) |
11 (11) |
14 (14) |
16 (16) |
18 (0) |
20 (2) |
21 (3) |
22 (4) |
23 (5) |
24 (6) |
25 (7) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +40.1 | +84.1 | -35.3 | +25.3 | -79.7 | -6.3 | +72.4 | -16.4 | +71.5 | -9.1 | -86.0 | +12.6 |
| Relative (%) | +23.3 | +48.8 | -20.5 | +14.7 | -46.2 | -3.7 | +42.0 | -9.5 | +41.5 | -5.3 | -49.9 | +7.3 | |
| Steps (reduced) |
26 (8) |
27 (9) |
27 (9) |
28 (10) |
28 (10) |
29 (11) |
30 (12) |
30 (12) |
31 (13) |
31 (13) |
31 (13) |
32 (14) | |
- Step size: 172.390 ¢, octave size: 1206.728 ¢
Stretching the octave of 7edo by around 7.3 ¢ results in much improved primes 3, 5 and 11, but much worse primes 2, 7 and 13. Its 2.3.5.11.13 WE tuning and 2.3.5.11.13 TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +6.7 | -5.7 | +13.5 | -28.1 | +1.1 | +79.0 | +20.2 | -11.3 | -21.3 | -14.0 | +7.8 |
| Relative (%) | +3.9 | -3.3 | +7.8 | -16.3 | +0.6 | +45.8 | +11.7 | -6.6 | -12.4 | -8.1 | +4.5 | |
| Step | 7 | 11 | 14 | 16 | 18 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +41.6 | +85.7 | -33.7 | +26.9 | -78.0 | -4.6 | +74.2 | -14.6 | +73.3 | -7.2 | -84.2 | +14.5 |
| Relative (%) | +24.1 | +49.7 | -19.6 | +15.6 | -45.3 | -2.7 | +43.0 | -8.5 | +42.5 | -4.2 | -48.8 | +8.4 | |
| Step | 26 | 27 | 27 | 28 | 28 | 29 | 30 | 30 | 31 | 31 | 31 | 32 | |
- Step size: 172.495 ¢, octave size: 1207.471 ¢
Stretching the octave of 7edo by around 7.5 ¢ results in much improved primes 3, 5 and 11, but much worse primes 2, 7 and 13. The tuning 15zpi does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +7.5 | -4.5 | +14.9 | -26.4 | +3.0 | +81.1 | +22.4 | -9.0 | -18.9 | -11.4 | +10.4 |
| Relative (%) | +4.3 | -2.6 | +8.7 | -15.3 | +1.7 | +47.0 | +13.0 | -5.2 | -11.0 | -6.6 | +6.1 | |
| Step | 7 | 11 | 14 | 16 | 18 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +44.4 | -83.9 | -30.9 | +29.9 | -75.1 | -1.5 | +77.4 | -11.4 | +76.6 | -3.9 | -80.9 | +17.9 |
| Relative (%) | +25.7 | -48.7 | -17.9 | +17.3 | -43.5 | -0.9 | +44.8 | -6.6 | +44.4 | -2.3 | -46.9 | +10.4 | |
| Step | 26 | 26 | 27 | 28 | 28 | 29 | 30 | 30 | 31 | 31 | 31 | 32 | |
- Step size: 172.905 ¢, octave size: 1210.335 ¢
Stretching the octave of 7edo by around 10.3 ¢ results in much improved primes 3, 5 and 11, but much worse primes 2, 7 and 13. The tuning 11edt does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +10.3 | +0.0 | +20.7 | -19.8 | +10.3 | -83.6 | +31.0 | +0.0 | -9.5 | -1.6 | +20.7 |
| Relative (%) | +6.0 | +0.0 | +12.0 | -11.5 | +6.0 | -48.4 | +17.9 | +0.0 | -5.5 | -0.9 | +12.0 | |
| Steps (reduced) |
7 (7) |
11 (0) |
14 (3) |
16 (5) |
18 (7) |
19 (8) |
21 (10) |
22 (0) |
23 (1) |
24 (2) |
25 (3) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +55.0 | -73.3 | -19.8 | +41.3 | -63.6 | +10.3 | -83.3 | +0.8 | -83.6 | +8.7 | -68.2 | +31.0 |
| Relative (%) | +31.8 | -42.4 | -11.5 | +23.9 | -36.8 | +6.0 | -48.2 | +0.5 | -48.4 | +5.1 | -39.5 | +17.9 | |
| Steps (reduced) |
26 (4) |
26 (4) |
27 (5) |
28 (6) |
28 (6) |
29 (7) |
29 (7) |
30 (8) |
30 (8) |
31 (9) |
31 (9) |
32 (10) | |
Instruments
Music
- See also: Category:7edo tracks
Ear training
7edo ear-training exercises by Alex Ness available here.
Notes
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
References
- ↑ African music, Encyclopedia Britannica.
- ↑ Robotham, Donald Keith and Gerhard Kubik.
- ↑ Nambiyathiri, Tarjani. Indian Music History And Structure Emmie Te Nijenhuis Brill
- ↑ Garzoli, John. The Myth of Equidistance in Thai Tuning.
