21edo

Prime factorization

3 × 7

Step size

57.1429¢

Fifth

12\21 (685.714¢) (→4\7)

Semitones (A1:m2)

0:3 (0¢ : 171.4¢)

Consistency limit

3

Distinct consistency limit

3

21 equal divisions of the octave (abbreviated 21edo or 21ed2), also called 21-tone equal temperament (21tet) or 21 equal temperament (21et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 21 equal parts of about 57.1 ¢ each. Each step represents a frequency ratio of 2^1/21, or the 21st root of 2.

Theory

Approximation of odd harmonics in 21edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23	25	27	29
Error	Absolute (¢)	-16.2	+13.7	+2.6	+24.7	+20.1	+16.6	-2.6	+9.3	-11.8	-13.6	+0.3	+27.4	+8.4	-1.0
Error	Relative (%)	-28.4	+24.0	+4.6	+43.2	+35.2	+29.1	-4.5	+16.3	-20.6	-23.9	+0.5	+47.9	+14.7	-1.8
Steps (reduced)		33 (12)	49 (7)	59 (17)	67 (4)	73 (10)	78 (15)	82 (19)	86 (2)	89 (5)	92 (8)	95 (11)	98 (14)	100 (16)	102 (18)

21edo provides both 7edo as a subset and the familiar 400-cent major third, while also giving some higher-limit JI possibilities. The system can be treated as three intertwining 7edo or "equiheptatonic" scales, or as seven 3edo augmented triads. The 7/4 at 971.43 ¢ is only off in 21edo by 2.60 ¢ from just (968.83 ¢), which is better than any other edo below 26.

In diatonically-related terms, 21edo possesses four types of 2nd (subminor, minor, submajor, and supermajor), three types of 3rd (subminor, neutral, and major), a "third-fourth" (an interval that can function as either a supermajor 3rd or a narrow 4th), a wide (or acute) 4th, and a narrow tritone, as well as the octave-inversions of all of these intervals.

Of harmonics 3, 5, 7, 11, and 13, the only harmonic 21edo approximates with anything approaching a near-just flavor is the 7th harmonic. On the other hand, 21edo provides exceptionally accurate tunings of the 15th, 23rd, and 29th harmonics (within 3 ¢ or less), as well as a very reasonable approximation of the 27th harmonic (around 8 ¢ sharp). As such, treating 21edo as a 2.7.15.23.27.29 subgroup temperament allows for a more accurate JI interpretation of the tuning, since almost every interval in 21edo can be described as a ratio within the 29-odd-limit. 21edo also works well on the 2.9/5.11/5.13/5.17/5.35/5 subgroup, which is possibly a more sensible way to treat it.

Intervals

Degree	Cents	Ups and downs notation			5L 3s octotonic notation	Extended-diatonic interval name	Approximate Ratios *1	Approximate Ratios *2	Approximate Ratios *3
0	0.00	1	unison	C	C	Unison	1/1	1/1	1/1
1	57.14	^1 vv2	up unison, dud 2nd	^C vvD	C#	Subminor 2nd	28/27, 30/29	35/34, 36/35	64/63
2	114.29	^^1 v2	dup unison, down 2nd	^^C vD	Db	Minor 2nd	16/15, 15/14, 29/27	18/17	16/15, 25/24
3	171.43	2	2nd	D	D	Submajor 2nd	10/9, 32/29	10/9,11/10	9/8
4	228.57	^2 vv3	up 2nd, dud 3rd	^D vvE	D#	Supermajor 2nd	8/7	8/7	8/7, 10/9, 11/10
5	285.71	^^2 v3	dup 2nd, down 3rd	^^D vE	Eb	Subminor 3rd	27/23, 32/27	13/11, 20/17	6/5, 7/6
6	342.86	3	3rd	E	E	Neutral 3rd	28/23	11/9	16/13
7	400.00	^3 vv4	up 3rd, dud 4th	^E vvF	E#/Fb	Major 3rd	29/23	44/35	5/4, 9/7, 11/9, 14/11
8	457.14	^^3 v4	dup 3rd, down 4th	^^E vF	F	Third-fourth (naiadic)	30/23	13/10, 17/13, 22/17	13/10
9	514.29	4	4th	F	F#	Acute 4th	161/120, 256/189	35/26	4/3, 18/13
10	571.43	^4 vv5	up 4th, dud 5th	^F vvG	Gb	Narrow tritone	32/23	18/13	7/5, 11/8
11	628.57	^^4 v5	dup 4th, down 5th	^^F vG	G	Wide tritone	23/16	13/9	10/7, 16/11
12	685.71	5	5th	G	G#	Grave 5th	189/128, 240/161	52/35	3/2, 13/9
13	742.86	^5 vv6	up 5th, dud 6th	^G vvA	Hb	Fifth-sixth (cocytic)	23/15	17/11, 20/13, 26/17	20/13
14	800.00	^^5 v6	dup 5th, down 6th	^^G vA	H	Minor 6th	46/29	35/22	8/5, 11/7, 14/9, 18/11
15	857.14	6	6th	A	H#/Ab	Neutral 6th	23/14	18/11	13/8
16	914.29	^6 vv7	up 6th, dud 7th	^A vvB	A	Supermajor 6th	27/16, 46/27	17/10, 22/13	5/3, 12/7
17	971.43	^^6 v7	dup 6th, down 7th	^^A vB	A#	Subminor 7th	7/4	7/4	7/4, 9/5, 20/11
18	1028.57	7	7th	B	Bb	Supraminor 7th	29/16, 9/5	9/5, 20/11	16/9
19	1085.71	^7 vv8	up 7th, dud 8ve	^B vvC	B	Major 7th	15/8	17/9	15/8, 48/25
20	1142.86	^^7 v8	dup 7th, down 8ve	^^B vC	B#/Cb	Supermajor 7th	27/14, 29/15	35/18, 68/35	63/32
21	1200.00	8	8ve	C	C	Octave	2/1	2/1	2/1

∗1: based on treating 21edo as a 2.7.15.23.27.29 subgroup temperament

∗2: based on treating 21edo as a 2.9/5.11/5.13/5.17/5.35/5 subgroup temperament

∗3: based on treating 21edo as 13-limit laconic temperament

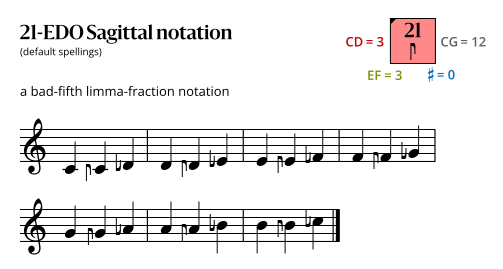
Chords

Chord names

Ups and downs can be used to name 21edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

0-6-12 = C E G = C = C or C perfect

0-5-12 = C vE G = Cv = C down

0-7-12 = C ^E G = C^ = C up

0-6-11 = C E vG = C(v5) = C down-five

0-7-13 = C ^E ^G = C^(^5) = C up up-five

0-6-12-18 = C E G B = C7 = C seven

0-6-12-17 = C E G vB = C,v7 = C add down-seven

0-5-12-18 = C vE G B = Cv,7 = C down add seven

0-5-12-17 = C vE G vB = Cv7 = C down-seven

For a more complete list, see Ups and downs notation#Chords and Chord Progressions.

Triadic harmony

One interesting feature of 21edo is the variety of triads it offers. Five of its intervals--228.6¢, 285.7¢, 342.9¢, 400¢, and 457.1¢ can function categorically as "3rds" for those whose ears are accustomed to diatonic interval categories, representing inframinor, minor, neutral, major, and ultramajor 3rds respectively (or dud, down, perfect, up and dup). One can couple these with 21edo's narrow fifth to form five types of triad. In addition to these, there are a few noteworthy "altered" triads that stand out as representations to parts of the harmonic series:

Steps	Cents	Ratio	Example in C	Written name	Spoken name
0-5-10	0-286-571	23:27:32	C vE vvG	Cv(vv5)	C down, dud five
0-4-11	0-229-629	7:8:10	C vvE vG	Cvv(v5)	C dud, down five
0-6-11	0-343-629	9:11:13	C E vG	C(v5)	C down-five
0-5-13	0-286-743	11:13:17	C vE ^G	Cv(^5)	C down up-five
0-8-13	0-457-743	13:17:20	C vF ^G	Cv4(^5)	C (sus) down-four up-five

Scales

MOS scales

Since 21edo contains sub-edos of 3 and 7, it contains no heptatonic MOS scales (other than 7edo and a few very hard scales) and a wealth of scales that repeat at a 1/3-octave period.

For 7-limit harmony (based on a chord of 0-7-12-17 approximating 4:5:6:7), using 1/3-octave period scales (i.e. those related to augmented temperament) yields the most harmonically-efficient scales. The 9-tone 3L 6s scale (related to Tcherepnin's scale in 12edo) is an excellent example.

For scales with a full-octave period, only 6 degrees of 21edo generate unique scales: 1\21, 2\21, 4\21, 5\21, 8\21, and 10\21. Other degrees generate either 7edo, 3edo, or a repetition of one of the other scales.

21edo has the soft oneirotonic (5L 3s) MOS with generator 8\21; in addition to the naiadics that generate it, it has neutral thirds (instead of major thirds as in 13edo oneirotonic), neogothic minor thirds, and Baroque diatonic semitones. The 4-oneirosteps are more tritone-like than fifth-like, unlike in 13edo, although they do have a consonant, even JI-like quality to them. In terms of JI, it mainly approximates 16:23:30, 16:23:29 and their inversions.

Periods per octave	Generator	MOSes
1	2\21	1L 9s 10L 1s
1	4\21	5L 1s 5L 6s
1	5\21	4L 1s 4L 5s 4L 9s
1	8\21	3L 2s 5L 3s 8L 5s
3	2\21	3L 3s 3L 6s 9L 3s
3	3\21	3L 3s 6L 3s 6L 9s
7	1\21	7L 7s

Rank-3 scales

The rank-3 scale diasem (323132313 or 313231323 in 21edo) is the 21edo tempering of Zarlino diatonic with 1\21 comma steps added, resulting in two "major seconds" (171 ¢ and 228 ¢), two "minor thirds" (286 ¢ and 343 ¢) and two "fourths" (457 ¢ and 514 ¢). 21edo is the smallest edo to support a non-degenerate diasem (with L:M:S ratio 3:2:1).

Tetrachordal scales

While 21edo lacks any 7-note MOS scales, one can still construct a variety of interesting and useful 7-note scales using tetrachords instead of MOS generators. The 21edo fourth is 9 steps, which can be divided into three parts in the following ways:

Step pattern	Cents	Example	Name*	Ups/downs name
3, 3, 3	(0)-171-343-(514)	C D E F	Equable diatonic	C perfect
4, 3, 2	(0)-229-400-(514)	C ^D ^E F	Soft diatonic	C up, up-2
4, 4, 1	(0)-229-457-(514)	C ^D ^^E F	Intense diatonic	C dup, up-2 & 6
5, 3, 1	(0)-286-457-(514)	C ^^D ^^E F	Archytas chromatic	C dup, dup-2
5, 2, 2	(0)-286-400-(514)	C ^^D ^E F	Weak chromatic	C up, dup 2 & 6
6, 2, 1	(0)-343-457-(514)	C ^3D ^^E F	Strong enharmonic	C dup, trup 2 & 6
7, 1, 1	(0)-400-457-(514)	C ^4D ^^E F	Pythagorean enharmonic	C dup, quadruple-up 2 & 6

∗These names may not be correct in relating to the ancient Greek tetrachordal genera; please change them if you know better!

The steps of these 7 basic patterns can also be permuted/rotated to give a total of 28 tetrachords, which can then be combined in either conjunct or disjunct form to yield a staggering number of scales. Thus 21 EDO can do reasonably-convincing imitations of the melodic forms of various tetrachordal musical traditions, such as ancient Greek, maqam, and dastgah.

Other scales

The subset 2 3 7 2 7 of 21edo (Pelog21) sounds similar to the Pelog lima mode of the Pelog scale.

The subset 2 5 5 6 3 of 21edo is a good tuning for the magnetosphere scale.

Regular temperament properties

The patent val for 21 EDO tempers out 128/125 and 2187/2000 in the 5-limit, and supplies the optimal patent val for the 5-limit laconic temperament tempering out 2187/2000, and also the optimal patent val for 7-, 11- and 13-limit gorgo, and 11- and 13-limit spartan. These temperaments lead to some "interesting" mappings, where 10/9 is larger than 9/8, 11/9 is larger than 16/13, and 8/7 maps to the same interval as 10/9, for instance.

Uniform maps

13-limit uniform maps between 20.5 and 21.5
Min. size	Max. size	Wart notation	Map
20.5000	20.5052	21bbcdeeefff	⟨21 32 48 58 71 76]
20.5052	20.6681	21cdeeefff	⟨21 33 48 58 71 76]
20.6681	20.6732	21cdefff	⟨21 33 48 58 72 76]
20.6732	20.8381	21cdef	⟨21 33 48 58 72 77]
20.8381	20.8878	21cef	⟨21 33 48 59 72 77]
20.8878	20.9435	21ef	⟨21 33 49 59 72 77]
20.9435	20.9572	21e	⟨21 33 49 59 72 78]
20.9572	21.1361	21	⟨21 33 49 59 73 78]
21.1361	21.1943	21b	⟨21 34 49 59 73 78]
21.1943	21.2137	21bdd	⟨21 34 49 60 73 78]
21.2137	21.2463	21bddff	⟨21 34 49 60 73 79]
21.2463	21.3185	21bddeeff	⟨21 34 49 60 74 79]
21.3185	21.4839	21bccddeeff	⟨21 34 50 60 74 79]
21.4839	21.5000	21bccddeeffff	⟨21 34 50 60 74 80]

Commas

21edo tempers out the following commas. (Note: This assumes the val ⟨21 33 49 59 73 78].)

Prime Limit	Ratio^[1]	Monzo	Cents	Color name	Name(s)
3	2187/2048	[-11 7⟩	113.69	Lawa	Apotome
5	128/125	[7 0 -3⟩	41.06	Trigu	Diesis, Augmented Comma
5	(16 digits)	[-25 7 6⟩	31.57	Lala-tribiyo	Ampersand, Ampersand's Comma
5	(20 digits)	[32 -7 -9⟩	9.49	Sasa-tritrigu	Escapade Comma
7	1029/1000	[-3 1 -3 3⟩	49.49	Trizogu	Keega
7	36/35	[2 2 -1 -1⟩	48.77	Rugu	Septimal Quarter Tone
7	(18 digits)	[-10 7 8 -7⟩	22.41	Lasepru-aquadbiyo	Blackjackisma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Septimal Kleisma, Marvel Comma
7	16875/16807	[0 3 4 -5⟩	6.99	Quinru-aquadyo	Mirkwai
7	2401/2400	[-5 -1 -2 4⟩	0.72	Bizozogu	Breedsma
7	(30 digits)	[47 -7 -7 -7⟩	0.34	Trisa-seprugu	Akjaysma, 5\7 Octave Comma
11	99/98	[-1 2 0 -2 1⟩	17.58	Loruru	Mothwellsma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Triluyo	Wizardharry