10edo

Prime factorization

2 × 5

Step size

120¢

Fifth

6\10 (720¢) (→3\5)

Semitones (A1:m2)

2:0 (240¢ : 0¢)

Consistency limit

7

Distinct consistency limit

3

Special properties

zeta peak
zeta peak integer

10 equal divisions of the octave (abbreviated 10edo or 10ed2), also called 10-tone equal temperament (10tet) or 10 equal temperament (10et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 10 equal parts of exactly 120 ¢ each. Each step represents a frequency ratio of 2^1/10, or the 10th root of 2.

Theory

10edo can be thought of as two circles of 5edo separated by 120 cents (or 5 circles of 2edo). It adds to 5edo a small neutral second (or large minor 2nd) and its inversion a large neutral seventh (or small major 7th); an excellent approximation of 13/8 and its inversion 16/13; and the familiar 600-cent tritone that appears in every even-numbered edo. Taking the the 360 cent large neutral third as a generator produces a heptatonic moment of symmetry scale of the form 1 2 1 2 1 2 1 (3L 4s - mosh), which is the most diatonic-like scale in 10edo excluding the 5edo degenerate diatonic scale. While not an integral or gap edo, it is a zeta peak edo. One way to interpret it in terms of a temperament of just intonation is as a 2.7.13.15 subgroup, such that 105/104, 225/224, 43904/43875 and 16807/16384 are tempered out. It can also be treated as a full 13-limit temperament, but it is a closer match to the aforementioned subgroup.

Prime harmonics

Approximation of prime harmonics in 10edo
Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	absolute (¢)	+0.0	+18.0	-26.3	-8.8	+48.7	-0.5	+15.0	-57.5	-28.3	+50.4	+55.0
Error	relative (%)	+0	+15	-22	-7	+41	-0	+13	-48	-24	+42	+46
Steps (reduced)		10 (0)	16 (6)	23 (3)	28 (8)	35 (5)	37 (7)	41 (1)	42 (2)	45 (5)	49 (9)	50 (0)

Intervals

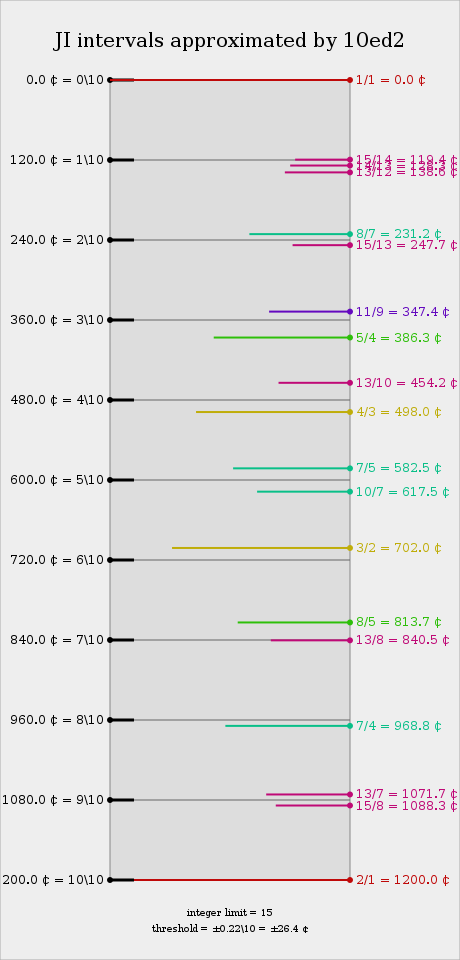
Degree	Cents	Approximate Ratios^[1]	Additional Ratios of 3, 5 and 9^[2]	Interval Names	Ups and Downs Notation			3L 4s notation
0	0	1/1	256/243, 50/49, 25/24	unison	unison, min 2nd	P1, m2	D, Eb	unison	C
1	120	16/15, 15/14, 14/13	10/9, 13/12, 81/80	neutral second	mid 2nd	~2	^D, vE	minor second	Db
2	240	8/7, 15/13, 144/125, 224/195	9/8, 7/6	hemifourth, major second, minor third	maj 2nd, min 3rd	M2, m3	E, F	major second, diminished third	D, Eb
3	360	16/13	5/4	neutral third	mid 3rd	~3	^F, vG	perfect/neutral third	E
4	480	64/49, 169/128	4/3, 9/7, 13/10	perfect fourth	maj 3rd, perf 4th	M3, P4	F#, G	minor fourth	Fb
5	600	91/64, 128/91, 169/120, 240/169	7/5, 10/7, 13/9, 18/13	hemioctave, tritone	up 4th, down 5th	^4, v5	^G, vA	major fourth, minor fifth	F, Gb
6	720	49/32, 256/169	3/2, 14/9, 20/13	perfect fifth	perf 5th, min 6th	P5, m6	A, Bb	major fifth	G
7	840	13/8	8/5	neutral sixth	mid 6th	~6	^A, vB	perfect/neutral sixth	A
8	960	7/4, 26/15, 125/72, 195/112	16/9, 12/7	hemitwelfth, major sixth, minor seventh	maj 6th, min 7th	M6, m7	B, C	augmented sixth, minor seventh	A#, Bb
9	1080	15/8, 28/15, 13/7	9/5, 24/13, 160/81	neutral seventh	mid 7th	~7	^C, vD	major seventh	B
10	1200	2/1	243/128, 49/25, 48/25	octave	maj 7th, octave	M7, P8	C#, D	octave	C

↑ based on treating 10edo as a 2.7.13.15 subgroup temperament
↑ adding the ratios of 3, 5 and 9 introduces greater error while giving several more harmonic identities to the 10-edo intervals

This is the diatonic notation, generated by 5ths (6\10, representing 3/2). Alternative notations include pentatonic fifth-generated and heptatonic 3rd-generated.

Pentatonic 5th-generated: D * E * G * A * C * D (generator = 3/2 = 6\10 = perfect 5thoid)

D - D^/Ev - E - E^/Gv - G - G^/Av - A - A^/Cv - C - C^/Dv - D

1 - ^1/vs3 - s3 - ^s3/v4d - 4d - ^4d/v5d - 5d - ^5d/vs7 - s7 - ^s7/v8d - 8d (s = sub-, d = -oid)

pentatonic gencircles of fifths: ...D - A - E - C - G - D... and ...^D - ^A - ^E - ^C - ^G - ^D... (or equivalently ...vD - vA - vE - vC - vG - vD...)

pentatonic gencircles of fifths: ...1 - 5d - s3 - s7 - 4d - 1... and ...^1 - ^5d - ^s3 - ^s7 - ^4d - ^1... (or equivalently ...v1 - v5d - vs3 - vs7 - v4d - v1...) (s = sub-, d = -oid)

Heptatonic 3rd-generated: D E * F G * A B * C D (generator = 3\10 = perfect 3rd)

D - E - E#/Fb - F - G - G#/Ab - A - B - B#/Cb - C - D

P1 - m2 - M2 - P3 - m4 - M4/m5 - M5 - P6 - m7 - M7 - P8

genchain of 3rds: ...Db - Fb - Ab - Cb - E - G - B - D - F - A - C - E# - G# - B# - D#... ("Every good boy deserves fudge and candy")

genchain of 3rds: ...d8 - d3 - m5 - m7 - m2 - m4 - P6 - P1 - P3 - M5 - M7 - M2 - M4 - A6 - A1...

Approximation to JI

Selected just intervals by error

Selected 13-limit intervals

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
Subgroup	Comma list	Mapping	Optimal 8ve Stretch (¢)	Absolute (¢)	Relative (%)
2.3.5	25/24, 256/243	[⟨10 16 23]]	-0.09	9.27	7.73
2.3.5.7	25/24, 28/27, 49/48	[⟨10 16 23 28]]	+0.72	8.15	6.79

10et is lower in relative error than any previous equal temperaments in the 7- and 17-limit. The next equal temperaments doing better in those subgroups are 12 and 19eg, respectively.
10et is prominent in the 2.3.7.13, 2.3.5.7.13, 2.3.7.13.17, and 2.3.5.7.13.17 subgroup. The next equal temperaments doing better in those subgroups are 17, 19, 36 and 31, respectively.

Uniform maps

13-limit uniform maps between 9.5 and 10.5
Min. size	Max. size	Wart notation	Map
9.5000	9.5935	10bccddeeeffff	⟨10 15 22 27 33 35]
9.5935	9.6837	10bccddeeeff	⟨10 15 22 27 33 36]
9.6837	9.6902	10bccddeff	⟨10 15 22 27 34 36]
9.6902	9.7794	10bddeff	⟨10 15 23 27 34 36]
9.7794	9.7957	10ddeff	⟨10 16 23 27 34 36]
9.7957	9.8637	10eff	⟨10 16 23 28 34 36]
9.8637	9.9727	10e	⟨10 16 23 28 34 37]
9.9727	10.1209	10	⟨10 16 23 28 35 37]
10.1209	10.1339	10c	⟨10 16 24 28 35 37]
10.1339	10.1519	10cf	⟨10 16 24 28 35 38]
10.1519	10.2618	10cdf	⟨10 16 24 29 35 38]
10.2618	10.4042	10cdeef	⟨10 16 24 29 36 38]
10.4042	10.4103	10cdeefff	⟨10 16 24 29 36 39]
10.4103	10.5000	10bbcdeefff	⟨10 17 24 29 36 39]

Commas

10et tempers out the following commas. This assumes the val ⟨10 16 23 28 35 37].

Prime Limit	Ratio^[1]	Monzo	Cents	Color Name	Name(s)
3	256/243	[8 -5⟩	90.22	Sawa	Limma, Pythagorean diatonic semitone
5	25/24	[-3 -1 2⟩	70.67	Yoyo	Classic chromatic semitone, dicot comma
5	16875/16384	[-14 3 4⟩	51.12	Laquadyo	Negri comma, double augmentation diesis
5	(16 digits)	[-25 7 6⟩	31.57	Lala-tribiyo	Ampersand, Ampersand's comma
5	2048/2025	[11 -4 -2⟩	19.55	Sagugu	Diaschisma
7	525/512	[-9 1 2 1⟩	43.41	Lazoyoyo	Avicennma, Avicenna's enharmonic diesis
7	49/48	[-4 -1 0 2⟩	35.70	Zozo	Slendro diesis
7	50/49	[1 0 2 -2⟩	34.98	Biruyo	Tritonic diesis, jubilisma
7	686/675	[1 -3 -2 3⟩	27.99	Trizo-agugu	Senga
7	64/63	[6 -2 0 -1⟩	27.26	Ru	Septimal comma, Archytas' comma, Leipziger Komma
7	(18 digits)	[-10 7 8 -7⟩	22.41	Lasepru-aquadbiyo	Blackjackisma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Septimal kleisma, marvel comma
7	16875/16807	[0 3 4 -5⟩	6.99	Quinru-aquadyo	Mirkwai
7	(24 digits)	[11 -10 -10 10⟩	5.57	Saquinbizogu	Linus
7	2401/2400	[-5 -1 -2 4⟩	0.72	Bizozogu	Breedsma
11	243/242	[-1 5 0 0 -2⟩	7.14	Lulu	Rastma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	441/440	[-3 2 -1 2 -1⟩	3.93	Luzozogu	Werckisma
11	540/539	[2 3 1 -2 -1⟩	3.21	Lururuyo	Swetisma
11	3025/3024	[-4 -3 2 -1 2⟩	0.57	Loloruyoyo	Lehmerisma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap
13	196/195	[2 -1 -1 2 0 -1⟩	8.86	Thuzozogu	Mynucuma
13	676/675	[2 -3 -2 0 0 2⟩	2.56	Bithogu	Island comma, parizeksma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Rank-2 temperaments

Periods per 8ve	Generator	Temperament(s)
1	1\10	Negri, miracle (out-of-tune)
1	3\10	Dicot / beatles / neutral
2	1\10	Pajara (out-of-tune)
2	2\10	Decimal, lemba (out-of-tune)
5	1\10	Blackwood / blacksmith

Scales

MOS scales

Decimal/Lemba[6] 4L 2s (period = 5\10, gen = 2\10): 2 2 1 2 2 1
Dicot[7] 3L 4s (gen = 3\10): 1 2 1 2 1 2 1
Negri[9] 1L 8s (gen = 1\10): 1 1 1 1 2 1 1 1 1

Other scales

Pinetone major pentatonic (subset of Dicot[7]): 2 1 3 1 3
Pinetone minor pentatonic (subset of Dicot[7]): 3 1 2 3 1
Marvel augmented hexatonic (subset of Dicot[7]): 2 1 3 1 2 1
Marvel double harmonic hexatonic (subset of Dicot[7]): 1 2 1 3 2 1, 1 2 3 1 2 1
Decimal/Lemba[6] 4M: 2 1 2 2 2 1
Dicot[7] 4M: 2 1 1 2 2 1 1

Horagrams

$1\10 MOS$

1\10 mos with 1L 1s, 1L 2s, 1L 3s, 1L 4s, 1L 5s, 1L 6s, 1L 7s, and 1L 8s

3\10 mos with 1L 1s, 1L 2s, 3L 1s, 3L 4s

Diagrams

Instruments

10edo lends itself exceptionally well to guitar (and other fretted strings), on account of the fact that five of its flat 4ths (at 480 cents) exactly spans two octaves (480 × 5 = 2400), meaning the open strings can be uniformly tuned in 4ths. This allows for greater uniformity in chord and scale fingering patterns than in 12edo, making it exceptionally easy to learn. For instance, the fingering for an "E" chord would be 0-2-2-1-0-0 (low to high), an "A" chord would be 0-0-2-2-1-0, and a "D" chord would be 1-0-0-2-2-1. This is also the case in all edos which are multiples of 5, but in 10-edo it is particularly simple.

Retuning a conventional keyboard to 10edo may be done in many ways, but neglecting or making redundant the Eb and Ab keys preserves the sLsLsLs scale on the white keys. Redundancy may make modulation easier, but another option is tuning the superfluous keys to selections from 20edo which approximates the 11th harmonic with relative accuracy, among other features.


A Decaphonic (10edo) Classical Guitar

Music

Main article: 10edo/Music

See also: Category:10edo tracks

[1] sed on treating 10edo as a 2.7.13.15 subgroup temperament

[2] the ratios of 3, 5 and 9 introduces greater error while giving several more harmonic identities to the 10-edo intervals

[3] Ratios longer than 10 digits are presented by placeholders with informative hints

[1]

[2]

[1]