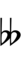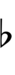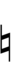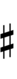33edo

← 32edo

33edo

34edo →

Prime factorization

3 × 11

Step size

36.3636 ¢

Fifth

19\33 (690.909 ¢)

Semitones (A1:m2)

1:4 (36.36 ¢ : 145.5 ¢)

Consistency limit

3

Distinct consistency limit

3

33 equal divisions of the octave (abbreviated 33edo or 33ed2), also called 33-tone equal temperament (33tet) or 33 equal temperament (33et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 33 equal parts of about 36.4 ¢ each. Each step represents a frequency ratio of 2^1/33, or the 33rd root of 2.

Theory

Structural properties

While relatively uncommon, 33edo is actually quite an interesting system. As a multiple of 11edo, it approximates the 7th and 11th harmonics via orgone temperament (see 26edo). 33edo also tunes the 13th harmonic slightly flat, allowing it to approximate the 21st and 17th harmonics as well, having a 3L 7s with L = 4, s = 3. The 33c (⟨33 52 76 93]) and 33cd (⟨33 52 76 92]) mappings temper out 81/80 and can be used to represent 1/2-comma meantone, a "flattertone" tuning where the whole tone is 10/9 in size. Indeed, the perfect fifth is tuned about 11 ¢ flat, and two stacked fifths fall only 0.6 ¢ flat of 10/9. Leaving the scale be would result in the standard diatonic scale (5L 2s) having minor seconds of four steps and whole tones of five steps. This also results in common practice minor and major chords becoming more supraminor and submajor in character, making everything sound almost neutral in quality.

Instead of the flat 19-step fifth you may use the 20-step sharp fifth, over 25 ¢ sharp. Two of these lead to a 9/8 of 7\33, which is about 22/19 in size and may be counted as a small third. Between the flat 5\33 version of 9/8 and the sharp 7\33 version there is, of course, a 6\33 = 2\11 interval of 218 ¢. Together, these add up to 6\33 + 5\33 = 11\33 = 1\3, or 400 ¢, the same major third as 12edo. We also have both a 327 ¢ minor third (9\33 = 6\22 = 3\11), the same as that of 22edo, and a flatter 8\33 third of 291 ¢, which if you like could also be called a flat 19th harmonic, but much more accurately a 13/11 sharp by 1.7 ¢ (if you use the patent val it is an extremely inaccurate 6/5). Another talent it has is that 7/5 is tuned quite accurately by 16\33, and we may put two 8\33 versions of 13/11 together to produce the cuthbert triad. The 8\33 generator, with MOS of size 5, 9, and 13, gives plenty of scope for these, as well as the 11th, 13th, and 19th harmonics (taking the generator as a 19/16) which are relatively well in tune.

33edo contains an accurate approximation of the Bohlen–Pierce scale with 4\33 near 1\13edt.

Other notable 33edo scales are diasem with L:m:s = 5:3:1 and 5L 4s with L:s = 5:2. This step ratio for 5L 4s is great for its semitone size of 72.7 ¢.

Odd harmonics

Approximation of odd harmonics in 33edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-11.0	+13.7	+13.0	+14.3	-5.9	-4.2	+2.6	+4.1	-6.6	+1.9	-10.1
Error	Relative (%)	-30.4	+37.6	+35.7	+39.2	-16.1	-11.5	+7.3	+11.4	-18.2	+5.4	-27.8
Steps (reduced)		52 (19)	77 (11)	93 (27)	105 (6)	114 (15)	122 (23)	129 (30)	135 (3)	140 (8)	145 (13)	149 (17)

33edo is not especially good at representing all rational intervals in the 7-limit, but it does very well on the 7-limit 3*33 subgroup 2.27.15.21.11.13. On this subgroup it tunes things to the same tuning as 99edo, and as a subgroup patent val it tempers out the same commas. The 99 equal temperaments hemififths, amity, parakleismic, hemiwuerschmidt, ennealimmal and hendecatonic can be reduced to this subgroup and give various possibilities for MOS scales, etc. In particular, the terrain 2.7/5.9/5 subgroup temperament can be tuned via the 5\33 generator. The full system of harmony provides the optimal patent val for slurpee temperament in the 5-, 7-, 11-, and 13-limits.

While it might not be the most harmonically accurate temperament, it is structurally quite interesting, and it approximates the full 19-limit consort in its own way. You could even say it tunes the 23rd and 29th harmonics ten cents flat if you were so inclined; as well as getting within two cents of the 37th.

Miscellany

33 is also the number of years in the Iranian calendar's leap cycle, where leap year is inserted once every 4 or 5 years. This corresponds to the 1L 7s with the step ratio of 5:4.

Intervals

Step #	ET	Just		Difference (ET minus Just)	Extended Pythagorean notation
Step #	Cents	Interval	Cents	Difference (ET minus Just)	Extended Pythagorean notation
0	0	1/1	0	0	Perfect Unison	P1	D
1	36.364	48/47	36.448	−0.085	Augmented Unison	A1	D#
2	72.727	24/23	73.681	−0.953	Double-aug 1sn	AA1	Dx
3	109.091	16/15	111.731	−2.640	Diminished 2nd	d2	Ebb
4	145.455	12/11	150.637	−5.183	Minor 2nd	m2	Eb
5	181.818	10/9	182.404	−0.586	Major 2nd	M2	E
6	218.182	17/15	216.687	+1.495	Augmented 2nd	A2	E#
7	254.545	15/13	247.741	+6.804	Double-aug 2nd/Double-dim 3rd	AA2/dd3	Ex/Fbb
8	290.909	13/11	289.210	+1.699	Diminished 3rd	d3	Fb
9	327.273	6/5	315.641	+11.631	Minor 3rd	m3	F
10	363.636	16/13	359.472	+4.164	Major 3rd	M3	F#
11	400.000	5/4	386.314	+13.686	Augmented 3rd	A3	Fx
12	436.364	9/7	435.084	+1.280	Double-dim 4th	dd4	Gbb
13	472.727	21/16	470.781	+1.946	Diminished 4th	d4	Gb
14	509.091	4/3	498.045	+11.046	Perfect 4th	P4	G
15	545.455	11/8	551.318	−5.863	Augmented 4th	A4	G#
16	581.818	7/5	582.513	−0.694	Double-aug 4th	AA4	Gx
17	618.182	10/7	617.488	+0.694	Double-dim 5th	dd5	Abb
18	654.545	16/11	648.682	+5.863	Diminished 5th	d5	Ab
19	690.909	3/2	701.955	−11.046	Perfect 5th	P5	A
20	727.273	32/21	729.219	-1.946	Augmented 5th	A5	A#
21	763.636	14/9	764.916	−1.280	Double-aug 5th	AA5	Ax
22	800.000	8/5	813.686	−13.686	Double-dim 6th	d6	Bbb
23	836.364	13/8	840.528	−4.164	Minor 6th	m6	Bb
24	872.727	5/3	884.359	−11.631	Major 6th	M6	B
25	909.091	22/13	910.790	−1.699	Augmented 6th	A6	B#
26	945.455	12/7	933.129	+12.325	Double-aug 6th/Double-dim 7th	AA6/dd7	Bx/Cbb
27	981.818	30/17	983.313	−1.495	Diminished 7th	d7	Cb
28	1018.182	9/5	1017.596	+0.586	Minor 7th	m7	C
29	1054.545	11/6	1049.363	+5.183	Major 7th	M7	C#
30	1090.909	15/8	1088.268	+2.640	Augmented 7th	A7	Cx
31	1127.273	23/12	1126.319	−0.953	Double-dim 8ve	dd8	Dbb
32	1163.636	47/24	1163.551	+0.085	Diminished 8ve	d8	Db
33	1200	2/1	1200	0	Perfect Octave	P8	D

Notation

Standard notation

Because the chromatic semitone in 33edo is 1 step, 33edo can be notated using only naturals, sharps, and flats. However, many key signatures will require double- and triple-sharps and flats, which means that notation in distant keys can be very unwieldy.

Step offset	−2	−1	0	+1	+2
Symbol

Sagittal notation

This notation uses the same sagittal sequence as EDOs 23 and 28.

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 33edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 33edo (direct approximation, even if inconsistent)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
9/5, 10/9	0.586	1.6
7/5, 10/7	0.694	1.9
9/7, 14/9	1.280	3.5
13/11, 22/13	1.699	4.7
15/8, 16/15	2.640	7.3
13/8, 16/13	4.164	11.5
11/6, 12/11	5.183	14.3
11/8, 16/11	5.863	16.1
15/13, 26/15	6.804	18.7
13/12, 24/13	6.882	18.9
15/11, 22/15	8.504	23.4
15/14, 28/15	10.352	28.5
3/2, 4/3	11.046	30.4
5/3, 6/5	11.631	32.0
7/6, 12/7	12.325	33.9
7/4, 8/7	12.992	35.7
5/4, 8/5	13.686	37.6
9/8, 16/9	14.272	39.2
11/9, 18/11	16.228	44.6
11/10, 20/11	16.814	46.2
13/7, 14/13	17.156	47.2
11/7, 14/11	17.508	48.1
13/10, 20/13	17.850	49.1
13/9, 18/13	17.928	49.3

15-odd-limit intervals in 33edo (patent val mapping)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
7/5, 10/7	0.694	1.9
13/11, 22/13	1.699	4.7
15/8, 16/15	2.640	7.3
13/8, 16/13	4.164	11.5
11/6, 12/11	5.183	14.3
11/8, 16/11	5.863	16.1
15/13, 26/15	6.804	18.7
13/12, 24/13	6.882	18.9
15/11, 22/15	8.504	23.4
15/14, 28/15	10.352	28.5
3/2, 4/3	11.046	30.4
7/4, 8/7	12.992	35.7
5/4, 8/5	13.686	37.6
11/9, 18/11	16.228	44.6
13/7, 14/13	17.156	47.2
13/10, 20/13	17.850	49.1
13/9, 18/13	17.928	49.3
11/7, 14/11	18.856	51.9
11/10, 20/11	19.550	53.8
9/8, 16/9	22.092	60.8
7/6, 12/7	24.038	66.1
5/3, 6/5	24.732	68.0
9/7, 14/9	35.084	96.5
9/5, 10/9	35.778	98.4

15-odd-limit intervals by 33cd val mapping
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
9/5, 10/9	0.586	1.6
7/5, 10/7	0.694	1.9
9/7, 14/9	1.280	3.5
13/11, 22/13	1.699	4.7
13/8, 16/13	4.164	11.5
11/6, 12/11	5.183	14.3
11/8, 16/11	5.863	16.1
13/12, 24/13	6.882	18.9
15/14, 28/15	10.352	28.5
3/2, 4/3	11.046	30.4
5/3, 6/5	11.631	32.0
7/6, 12/7	12.325	33.9
11/9, 18/11	16.228	44.6
11/10, 20/11	16.814	46.2
11/7, 14/11	17.508	48.1
13/9, 18/13	17.928	49.3
13/10, 20/13	18.513	50.9
13/7, 14/13	19.207	52.8
9/8, 16/9	22.092	60.8
5/4, 8/5	22.677	62.4
7/4, 8/7	23.371	64.3
15/11, 22/15	27.860	76.6
15/13, 26/15	29.559	81.3
15/8, 16/15	33.723	92.7

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Absolute (¢)	Relative (%)
2.3	[-52 33⟩	[⟨33 52]]	+3.48	3.49	9.59
2.3.5	81/80, 1171875/1048576	[⟨33 52 76]] (33c)	+5.59	4.13	11.29
2.3.5.7	49/48, 81/80, 1875/1792	[⟨33 52 76 92]] (33cd)	+6.29	3.77	10.31
2.3.5.7.11	45/44, 49/48, 81/80, 1375/1344	[⟨33 52 76 92 114]] (33cd)	+5.36	3.84	10.50
2.3.5.7.11.13	45/44, 49/48, 65/64, 81/80, 275/273	[⟨33 52 76 92 114 122]] (33cd)	+4.65	3.84	10.52

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperaments
1	2\33	72.73	21/20	Slurpee (33)
1	4\33	145.45	12/11	Bohpier (33cd)
1	7\33	254.55	8/7	Godzilla (33cd)
1	8\33	290.91	25/21	Quasitemp (33b)
1	10\33	363.64	49/40	Submajor (33ee) / interpental (33e)
1	14\33	509.09	4/3	Flattertone (33cd) Deeptone a.k.a. tragicomical (33)
1	16\33	581.82	7/5	Tritonic (33)
3	7\33 (4\33)	254.55 (145.45)	8/7 (12/11)	Triforce (33d)
3	13\33 (2\33)	472.73 (72.73)	4/3 (25/24)	Inflated (33bcddd)
3	14\33 (3\33)	509.09 (98.09)	4/3 (16/15)	August (33cd)

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Octave stretch or compression

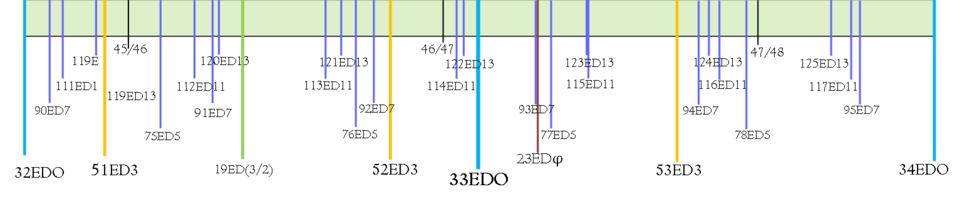
33edo is nearby to many other equal tunings which can act as stretched or compressed versions of 33edo, improving some of its harmonics at the expense of others.

What follows is a comparison of stretched- and compressed-octave 33edo tunings.

76ed5

Octave size: 1209.8 ¢

Stretching the octave of 33edo by around 10 ¢ results in improved primes 3 and 7, but worse primes 2 and 11. This approximates all harmonics up to 16 within 17.0 ¢. The tuning 76ed5 does this.

Approximation of harmonics in 76ed5
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+9.8	+4.5	-17.0	+0.0	+14.3	+4.1	-7.1	+8.9	+9.8	-8.5	-12.5
Error	Relative (%)	+26.9	+12.2	-46.3	+0.0	+39.1	+11.1	-19.4	+24.4	+26.9	-23.2	-34.1
Steps (reduced)		33 (33)	52 (52)	65 (65)	76 (0)	85 (9)	92 (16)	98 (22)	104 (28)	109 (33)	113 (37)	117 (41)

Approximation of harmonics in 76ed5 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-4.4	+13.9	+4.5	+2.7	+7.8	-17.9	-1.5	-17.0	+8.6	+1.3	-2.3	-2.7
Error	Relative (%)	-12.1	+38.0	+12.2	+7.4	+21.2	-48.8	-4.1	-46.3	+23.3	+3.6	-6.3	-7.2
Steps (reduced)		121 (45)	125 (49)	128 (52)	131 (55)	134 (58)	136 (60)	139 (63)	141 (65)	144 (68)	146 (70)	148 (72)	150 (74)

92ed7

Octave size: 1208.4 ¢

Stretching the octave of 33edo by around 8.5 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 17.7 ¢. The tuning 92ed7 does this. So does the tuning 137zpi whose octave differs by only 0.3 ¢.

Approximation of harmonics in 92ed7
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+8.4	+2.2	+16.8	-3.4	+10.5	+0.0	-11.5	+4.3	+5.0	-13.5	-17.7
Error	Relative (%)	+22.9	+5.9	+45.8	-9.2	+28.8	+0.0	-31.3	+11.8	+13.7	-36.9	-48.3
Steps (reduced)		33 (33)	52 (52)	66 (66)	76 (76)	85 (85)	92 (0)	98 (6)	104 (12)	109 (17)	113 (21)	117 (25)

Approximation of harmonics in 92ed7 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-9.8	+8.4	-1.2	-3.1	+1.8	+12.7	-7.7	+13.4	+2.2	-5.1	-8.9	-9.3
Error	Relative (%)	-26.7	+22.9	-3.3	-8.4	+5.0	+34.7	-20.9	+36.6	+5.9	-14.0	-24.2	-25.4
Steps (reduced)		121 (29)	125 (33)	128 (36)	131 (39)	134 (42)	137 (45)	139 (47)	142 (50)	144 (52)	146 (54)	148 (56)	150 (58)

52edt

Step size: 36.576, octave size: 1207.0 ¢

Stretching the octave of 33edo by around 7 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 14. This approximates all harmonics up to 16 within 18.2 ¢. The tuning 52edt does this.

Approximation of harmonics in 76ed5
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+7.0	+0.0	+14.0	-6.5	+7.0	-3.8	-15.5	+0.0	+0.5	-18.2	+14.0
Error	Relative (%)	+19.2	+0.0	+38.3	-17.9	+19.2	-10.5	-42.5	+0.0	+1.3	-49.8	+38.3
Steps (reduced)		33 (33)	52 (0)	66 (14)	76 (24)	85 (33)	92 (40)	98 (46)	104 (0)	109 (5)	113 (9)	118 (14)

Approximation of harmonics in 52edt (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-14.8	+3.2	-6.5	-8.5	-3.8	+7.0	-13.4	+7.5	-3.8	-11.2	-15.0	-15.5
Error	Relative (%)	-40.5	+8.7	-17.9	-23.3	-10.3	+19.2	-36.7	+20.5	-10.5	-30.7	-41.1	-42.5
Steps (reduced)		121 (17)	125 (21)	128 (24)	131 (27)	134 (30)	137 (33)	139 (35)	142 (38)	144 (40)	146 (42)	148 (44)	150 (46)

114ed11

Octave size: 1201.7 ¢

Stretching the octave of 33edo by around 2 ¢ results in improved primes 3, 11 and 13, but worse primes 2, 5 and 7. This approximates all harmonics up to 16 within 17.8 ¢. The tuning 114ed11 does this.

Approximation of harmonics in 114ed11
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+1.7	-8.4	+3.4	+17.6	-6.7	+17.8	+5.1	-16.7	-17.1	+0.0	-5.0
Error	Relative (%)	+4.7	-23.0	+9.3	+48.5	-18.3	+48.8	+14.0	-46.0	-46.9	+0.0	-13.7
Steps (reduced)		33 (33)	52 (52)	66 (66)	77 (77)	85 (85)	93 (93)	99 (99)	104 (104)	109 (109)	114 (0)	118 (4)

Approximation of harmonics in 114ed11 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+2.1	-16.9	+9.3	+6.8	+11.1	-15.0	+0.6	-15.4	+9.4	+1.7	-2.4	-3.3
Error	Relative (%)	+5.8	-46.5	+25.5	+18.6	+30.4	-41.3	+1.6	-42.2	+25.8	+4.7	-6.7	-9.0
Steps (reduced)		122 (8)	125 (11)	129 (15)	132 (18)	135 (21)	137 (23)	140 (26)	142 (28)	145 (31)	147 (33)	149 (35)	151 (37)

138zpi

Step size: 36.394 ¢, octave size: 1201.0 ¢

Stretching the octave of 33edo by around 1 ¢ results in improved primes 3, 11 and 13, but worse primes 2, 5 and 7. This approximates all harmonics up to 16 within 17.5 ¢. The tuning 138zpi does this. So does the tuning 122ed13 whose octave differs by only 0.1 ¢.

Approximation of harmonics in 138zpi
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+1.0	-9.5	+2.0	+16.0	-8.5	+15.8	+3.0	+17.5	+17.0	-2.4	-7.5
Error	Relative (%)	+2.8	-26.0	+5.5	+44.0	-23.3	+43.5	+8.3	+48.0	+46.8	-6.6	-20.5
Step		33	52	66	77	85	93	99	105	110	114	118

Approximation of harmonics in 138zpi (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-0.5	+16.8	+6.6	+4.0	+8.2	-17.9	-2.4	+18.0	+6.3	-1.4	-5.6	-6.5
Error	Relative (%)	-1.3	+46.2	+18.0	+11.0	+22.6	-49.3	-6.5	+49.5	+17.4	-3.8	-15.3	-17.8
Step		122	126	129	132	135	137	140	143	145	147	149	151

33edo

Step size: 36.363 ¢, octave size: 1200.0 ¢

Pure-octaves 33edo approximates all harmonics up to 16 within 14.3 ¢.

Approximation of harmonics in 33edo
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+0.0	-11.0	+0.0	+13.7	-11.0	+13.0	+0.0	+14.3	+13.7	-5.9	-11.0
Error	Relative (%)	+0.0	-30.4	+0.0	+37.6	-30.4	+35.7	+0.0	+39.2	+37.6	-16.1	-30.4
Steps (reduced)		33 (0)	52 (19)	66 (0)	77 (11)	85 (19)	93 (27)	99 (0)	105 (6)	110 (11)	114 (15)	118 (19)

Approximation of harmonics in 33edo (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-4.2	+13.0	+2.6	+0.0	+4.1	+14.3	-6.6	+13.7	+1.9	-5.9	-10.1	-11.0
Error	Relative (%)	-11.5	+35.7	+7.3	+0.0	+11.4	+39.2	-18.2	+37.6	+5.4	-16.1	-27.8	-30.4
Steps (reduced)		122 (23)	126 (27)	129 (30)	132 (0)	135 (3)	138 (6)	140 (8)	143 (11)	145 (13)	147 (15)	149 (17)	151 (19)

33et, 13-limit WE tuning

Step size: 36.357 ¢, octave size: 1199.8 ¢

Compressing the octave of 33edo by a fifth of a cent results in improved primes 5 and 7, but worse primes 2, 3, 11 and 13. This approximates all harmonics up to 16 within 13.6 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.

Approximation of harmonics in 33et, 13-limit WE tuning
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-0.2	-11.4	-0.4	+13.2	-11.6	+12.4	-0.7	+13.6	+13.0	-6.6	-11.8
Error	Relative (%)	-0.6	-31.3	-1.2	+36.2	-31.9	+34.0	-1.8	+37.3	+35.6	-18.2	-32.5
Step		33	52	66	77	85	93	99	105	110	114	118

Approximation of harmonics in 33et, 13-limit WE tuning (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-5.0	+12.2	+1.8	-0.9	+3.2	+13.4	-7.5	+12.7	+1.0	-6.8	-11.1	-12.0
Error	Relative (%)	-13.7	+33.4	+4.9	-2.4	+8.9	+36.7	-20.7	+35.0	+2.7	-18.8	-30.5	-33.1
Step		122	126	129	132	135	138	140	143	145	147	149	151

93ed7

Octave size: 1196.4 ¢

Compressing the octave of 33edo by around 4.5 ¢ results in improved primes 5 and 7, but worse primes 2, 3, 11 and 13. This approximates all harmonics up to 16 within 17.9 ¢. If one wishes to use both 33edo's sharp and flat fifths simultaneously (see dual-fifth tuning), then this amount of stretch is ideal, because it evenly shares error between the two fifths. The tuning 93ed7 does this. So does the tuning 52ed13 whose octave differs by only 0.1 ¢.

Approximation of harmonics in 93ed7
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-4.6	+17.9	-9.2	+2.9	+13.3	+0.0	-13.8	-0.4	-1.7	+14.4	+8.7
Error	Relative (%)	-12.7	+49.5	-25.5	+8.1	+36.7	+0.0	-38.2	-1.1	-4.6	+39.8	+24.0
Steps (reduced)		33 (33)	53 (53)	66 (66)	77 (77)	86 (86)	93 (0)	99 (6)	105 (12)	110 (17)	115 (22)	119 (26)

Approximation of harmonics in 93ed7 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+15.0	-4.6	-15.4	+17.8	-14.7	-5.0	+10.1	-6.3	+17.9	+9.8	+5.3	+4.1
Error	Relative (%)	+41.5	-12.7	-42.5	+49.1	-40.6	-13.8	+27.8	-17.4	+49.5	+27.1	+14.7	+11.3
Steps (reduced)		123 (30)	126 (33)	129 (36)	133 (40)	135 (42)	138 (45)	141 (48)	143 (50)	146 (53)	148 (55)	150 (57)	152 (59)

77ed5

Octave size: 1194.1 ¢

Compressing the octave of 33edo by around 6 ¢ results in improved primes 5 and 7, but worse primes 2, 3, 11 and 13. This approximates all harmonics up to 16 within 17.6 ¢. The tuning 77ed5 does this. So does the tuning 139zpi whose octave differs by only 0.2 ¢.

Approximation of harmonics in 77ed5
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-5.9	+15.9	-11.7	+0.0	+10.0	-3.5	-17.6	-4.4	-5.9	+10.1	+4.2
Error	Relative (%)	-16.2	+43.9	-32.4	+0.0	+27.7	-9.8	-48.6	-12.1	-16.2	+27.8	+11.5
Steps (reduced)		33 (33)	53 (53)	66 (66)	77 (0)	86 (9)	93 (16)	99 (22)	105 (28)	110 (33)	115 (38)	119 (42)

Approximation of harmonics in 77ed5 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+10.3	-9.4	+15.9	+12.7	+16.3	-10.3	+4.7	-11.7	+12.4	+4.2	-0.4	-1.7
Error	Relative (%)	+28.6	-26.0	+43.9	+35.2	+45.1	-28.3	+13.0	-32.4	+34.2	+11.6	-1.1	-4.7
Steps (reduced)		123 (46)	126 (49)	130 (53)	133 (56)	136 (59)	138 (61)	141 (64)	143 (66)	146 (69)	148 (71)	150 (73)	152 (75)

115ed11

Octave size: 1191.2 ¢

Compressing the octave of 33edo by around 9 ¢ results in improved primes 5, 7, 11 and 13, but a worse prime 2. This approximates all harmonics up to 16 within 17.5 ¢. The tuning 115ed11 does this. So do the tunings 123ed13 and 1ed47/46 whose octaves are within 0.3 ¢ of 115ed11.

Approximation of harmonics in 115ed11
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-8.8	+11.3	-17.5	-6.7	+2.5	-11.7	+9.8	-13.6	-15.5	+0.0	-6.2
Error	Relative (%)	-24.2	+31.2	-48.5	-18.7	+7.0	-32.3	+27.3	-37.6	-42.9	+0.0	-17.3
Steps (reduced)		33 (33)	53 (53)	66 (66)	77 (77)	86 (86)	93 (93)	100 (100)	105 (105)	110 (110)	115 (0)	119 (4)

Approximation of harmonics in 115ed11 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-0.4	+15.7	+4.5	+1.1	+4.4	+13.8	-7.6	+11.9	-0.4	-8.8	-13.5	-15.0
Error	Relative (%)	-1.2	+43.4	+12.5	+3.0	+12.3	+38.1	-21.2	+32.8	-1.1	-24.2	-37.4	-41.5
Steps (reduced)		123 (8)	127 (12)	130 (15)	133 (18)	136 (21)	139 (24)	141 (26)	144 (29)	146 (31)	148 (33)	150 (35)	152 (37)

Scales

Main article: List of MOS scales in 33edo

Brightest mode is listed except where noted.

Deeptone[7], 5 5 5 4 5 5 4 (diatonic)
- Fun 5-tone subset of Deeptone[7] 9 5 5 4 10
Deeptone[12], 4 4 1 4 1 4 4 1 4 1 4 1 (chromatic)
Deeptone[19], 3 1 3 1 1 3 1 1 3 1 3 1 1 3 1 1 3 1 1 (enharmonic)
Semiquartal, 5 5 2 5 2 5 2 5 2
Semiquartal[14], 3 2 3 2 2 3 2 2 3 2 2
Iranian Calendar, 5 4 4 4 4 4 4 4
Diasem, 5 3 5 1 5 3 5 1 5 (*right-handed)
Diasem, 5 1 5 3 5 1 5 3 5 (*left-handed)
Diaslen (4sR), 1 5 1 5 2 5 1 5 1 5 2
Diaslen (4sL), 2 5 1 5 1 5 2 5 1 5 1
Diaslen (4sC), 1 5 2 5 1 5 1 5 2 5 1

Delta-rational harmony

The tables below show chords that approximate 3-integer-limit delta-rational chords with least-squares error less than 0.001.

Fully delta-rational triads

Steps	Delta signature	Least-squares error
0,1,2	+1+1	0.00021
0,1,3	+1+2	0.00048
0,1,4	+1+3	0.00078
0,2,3	+2+1	0.00039
0,2,4	+1+1	0.00087
0,3,4	+3+1	0.00056
0,3,11	+1+3	0.00007
0,5,8	+3+2	0.00084
0,8,18	+2+3	0.00082
0,9,20	+2+3	0.00076
0,12,17	+2+1	0.00048
0,13,20	+3+2	0.00063
0,15,21	+2+1	0.00063
0,16,28	+1+1	0.00082
0,18,25	+2+1	0.00081
0,18,31	+1+1	0.00058
0,19,24	+3+1	0.00095

Partially delta-rational tetrads

Steps	Delta signature	Least-squares error
0,1,2,3	+1+?+1	0.00053
0,1,2,4	+1+?+2	0.00094
0,1,3,4	+1+?+1	0.00080
0,1,17,18	+2+?+3	0.00073
0,1,17,19	+1+?+3	0.00071
0,1,18,19	+2+?+3	0.00042
0,1,18,20	+1+?+3	0.00032
0,1,19,20	+2+?+3	0.00010
0,1,19,21	+1+?+3	0.00008
0,1,20,21	+2+?+3	0.00023
0,1,20,22	+1+?+3	0.00049
0,1,21,22	+2+?+3	0.00056
0,1,21,23	+1+?+3	0.00091
0,1,22,23	+2+?+3	0.00090
0,1,31,32	+1+?+2	0.00071
0,2,3,4	+2+?+1	0.00077
0,2,6,11	+1+?+3	0.00094
0,2,7,12	+1+?+3	0.00013
0,2,8,13	+1+?+3	0.00069
0,2,12,13	+3+?+2	0.00083
0,2,12,15	+1+?+2	0.00087
0,2,13,14	+3+?+2	0.00045
0,2,13,16	+1+?+2	0.00014
0,2,14,15	+3+?+2	0.00008
0,2,14,17	+1+?+2	0.00060
0,2,15,16	+3+?+2	0.00031
0,2,16,17	+3+?+2	0.00071
0,2,18,20	+2+?+3	0.00084
0,2,18,22	+1+?+3	0.00024
0,2,19,21	+2+?+3	0.00020
0,2,19,23	+1+?+3	0.00058
0,2,20,22	+2+?+3	0.00046
0,3,4,5	+3+?+1	0.00097
0,3,5,9	+2+?+3	0.00010
0,3,6,10	+2+?+3	0.00090
0,3,7,12	+1+?+2	0.00074
0,3,8,13	+1+?+2	0.00037
0,3,10,17	+1+?+3	0.00009
0,3,17,23	+1+?+3	0.00096
0,3,18,22	+1+?+2	0.00088
0,3,18,24	+1+?+3	0.00027
0,3,19,20	+2+?+1	0.00059
0,3,19,21	+1+?+1	0.00063
0,3,19,22	+2+?+3	0.00030
0,3,19,23	+1+?+2	0.00023
0,3,20,21	+2+?+1	0.00014
0,3,20,22	+1+?+1	0.00015
0,3,20,23	+2+?+3	0.00070
0,3,21,22	+2+?+1	0.00032
0,3,21,23	+1+?+1	0.00095
0,3,22,23	+2+?+1	0.00078
0,3,27,32	+1+?+3	0.00004
0,4,5,12	+1+?+2	0.00026
0,4,6,16	+1+?+3	0.00066
0,4,8,13	+2+?+3	0.00023
0,4,11,20	+1+?+3	0.00023
0,4,13,14	+3+?+1	0.00091
0,4,13,19	+1+?+2	0.00048
0,4,14,15	+3+?+1	0.00050
0,4,14,16	+3+?+2	0.00055
0,4,14,17	+1+?+1	0.00021
0,4,15,16	+3+?+1	0.00009
0,4,15,17	+3+?+2	0.00023
0,4,15,18	+1+?+1	0.00085
0,4,16,17	+3+?+1	0.00034
0,4,17,18	+3+?+1	0.00077
0,4,17,25	+1+?+3	0.00043
0,4,19,23	+2+?+3	0.00041
0,4,20,24	+2+?+3	0.00094
0,4,22,27	+1+?+2	0.00020
0,4,24,31	+1+?+3	0.00022
0,5,6,9	+3+?+2	0.00003
0,5,7,10	+3+?+2	0.00097
0,5,7,19	+1+?+3	0.00004
0,5,9,17	+1+?+2	0.00017
0,5,10,16	+2+?+3	0.00019
0,5,11,13	+2+?+1	0.00087
0,5,11,15	+1+?+1	0.00018
0,5,12,14	+2+?+1	0.00011
0,5,12,23	+1+?+3	0.00067
0,5,13,15	+2+?+1	0.00067
0,5,16,23	+1+?+2	0.00008
0,5,17,27	+1+?+3	0.00055
0,5,19,24	+2+?+3	0.00051
0,5,22,31	+1+?+3	0.00057
0,5,24,30	+1+?+2	0.00036
0,5,25,26	+3+?+1	0.00071
0,5,25,27	+3+?+2	0.00082
0,5,25,28	+1+?+1	0.00045
0,5,26,27	+3+?+1	0.00018
0,5,26,28	+3+?+2	0.00016
0,5,26,29	+1+?+1	0.00090
0,5,27,28	+3+?+1	0.00035
0,5,28,29	+3+?+1	0.00090
0,6,7,17	+1+?+2	0.00087
0,6,8,22	+1+?+3	0.00045
0,6,9,14	+1+?+1	0.00031
0,6,11,18	+2+?+3	0.00093
0,6,12,21	+1+?+2	0.00036
0,6,12,25	+1+?+3	0.00032
0,6,15,18	+3+?+2	0.00026
0,6,16,19	+3+?+2	0.00095
0,6,16,28	+1+?+3	0.00053
0,6,18,26	+1+?+2	0.00064
0,6,19,25	+2+?+3	0.00062
0,6,20,24	+1+?+1	0.00052
0,6,21,23	+2+?+1	0.00031
0,6,21,32	+1+?+3	0.00033
0,6,22,24	+2+?+1	0.00063
0,6,25,32	+1+?+2	0.00034
0,7,8,14	+1+?+1	0.00029
0,7,8,24	+1+?+3	0.00080
0,7,9,11	+3+?+1	0.00066
0,7,9,12	+2+?+1	0.00041
0,7,9,13	+3+?+2	0.00019
0,7,10,12	+3+?+1	0.00009
0,7,10,13	+2+?+1	0.00070
0,7,11,13	+3+?+1	0.00087
0,7,12,27	+1+?+3	0.00041
0,7,16,30	+1+?+3	0.00098
0,7,17,22	+1+?+1	0.00008
0,7,19,26	+2+?+3	0.00073
0,7,20,29	+1+?+2	0.00002
0,7,23,26	+3+?+2	0.00010
0,7,28,32	+1+?+1	0.00033
0,7,29,31	+2+?+1	0.00020
0,7,30,32	+2+?+1	0.00091
0,8,12,29	+1+?+3	0.00097
0,8,13,22	+2+?+3	0.00051
0,8,15,21	+1+?+1	0.00062
0,8,15,31	+1+?+3	0.00047
0,8,16,18	+3+?+1	0.00066
0,8,16,19	+2+?+1	0.00031
0,8,16,20	+3+?+2	0.00043
0,8,16,27	+1+?+2	0.00090
0,8,17,19	+3+?+1	0.00022
0,8,17,20	+2+?+1	0.00098
0,8,19,27	+2+?+3	0.00085
0,8,24,29	+1+?+1	0.00020
0,9,11,16	+3+?+2	0.00051
0,9,13,20	+1+?+1	0.00002
0,9,14,24	+2+?+3	0.00073
0,9,18,30	+1+?+2	0.00090
0,9,19,28	+2+?+3	0.00096
0,9,21,27	+1+?+1	0.00040
0,9,22,24	+3+?+1	0.00087
0,9,22,25	+2+?+1	0.00053
0,9,22,26	+3+?+2	0.00026
0,9,23,25	+3+?+1	0.00013
0,9,23,26	+2+?+1	0.00093
0,10,11,26	+1+?+2	0.00035
0,10,11,32	+1+?+3	0.00081
0,10,12,20	+1+?+1	0.00098
0,10,14,18	+2+?+1	0.00050
0,10,14,25	+2+?+3	0.00088
0,10,15,29	+1+?+2	0.00041
0,10,16,21	+3+?+2	0.00055
0,10,19,32	+1+?+2	0.00021
0,10,27,31	+3+?+2	0.00082
0,10,28,30	+3+?+1	0.00045
0,10,28,31	+2+?+1	0.00016
0,10,29,31	+3+?+1	0.00068
0,11,12,18	+3+?+2	0.00030
0,11,13,16	+3+?+1	0.00081
0,11,14,17	+3+?+1	0.00044
0,11,16,31	+1+?+2	0.00064
0,11,17,25	+1+?+1	0.00091
0,11,19,23	+2+?+1	0.00045
0,11,21,26	+3+?+2	0.00074
0,12,15,24	+1+?+1	0.00087
0,12,15,28	+2+?+3	0.00013
0,12,17,23	+3+?+2	0.00054
0,12,18,21	+3+?+1	0.00043
0,12,19,22	+3+?+1	0.00095
0,12,23,27	+2+?+1	0.00083
0,12,26,31	+3+?+2	0.00005
0,13,14,24	+1+?+1	0.00019
0,13,17,22	+2+?+1	0.00085
0,13,21,27	+3+?+2	0.00035
0,13,22,25	+3+?+1	0.00097
0,13,23,26	+3+?+1	0.00054
0,13,28,32	+2+?+1	0.00055
0,14,17,24	+3+?+2	0.00099
0,14,18,28	+1+?+1	0.00043
0,14,21,26	+2+?+1	0.00080
0,14,25,31	+3+?+2	0.00054
0,14,27,30	+3+?+1	0.00050
0,15,16,20	+3+?+1	0.00055
0,15,17,28	+1+?+1	0.00064
0,15,21,28	+3+?+2	0.00045
0,15,22,32	+1+?+1	0.00039
0,16,18,26	+3+?+2	0.00049
0,16,19,25	+2+?+1	0.00031
0,16,20,24	+3+?+1	0.00018
0,16,25,32	+3+?+2	0.00095
0,17,22,28	+2+?+1	0.00091
0,17,23,27	+3+?+1	0.00066
0,18,27,31	+3+?+1	0.00095
0,19,21,28	+2+?+1	0.00065
0,20,24,31	+2+?+1	0.00078
0,21,22,32	+3+?+2	0.00091
0,22,27,32	+3+?+1	0.00038