Middle Path table of seven-limit rank two temperaments
This table is an updated version of Table 2 of Paul Erlich's A Middle Path. The complexity is now measured a different way (which, however, is proportional to the original complexity for this table), and some temperament names have been updated.
This table comprises all possible 7-limit rank-2 cases where complexity/7.65 + damage/10 < 1.
| Vanishing interval's ratios | Temperament name |
TOP period |
TOP generator |
Mapp. of 2 |
Mapp. of 3 |
Mapp. of 5 |
Mapp. of 7 |
Cmplx | TOP Dmg |
ETs |
|---|---|---|---|---|---|---|---|---|---|---|
| 28/27, 49/48, 64/63, 256/243, 343/324, … | Blacksmith | 239.18 | 155.35 | 5,0 | 8,0 | 11,1 | 14,0 | 2.01 | 7.24 | 15, 25, (30), 35bc, 40b, (45bc), 50bc, (50b), … |
| 36/35, 50/49, 126/125, 360/343, 648/625, … | Diminished | 298.53 | 197.08 | 4,0 | 7,-1 | 10,-1 | 12,-1 | 2.46 | 5.87 | 12, (24d), (36d), (48cdd), 56cddd, (60cddd), … |
| 36/35, 64/63, 81/80, 256/245, 729/700, … | Dominant | 1195.23 | 495.88 | 1,0 | 2,-1 | 4,-4 | 2,2 | 2.47 | 4.77 | 12, (24d), 29cd, (36d), 41cd, 46ccd, (48cdd), … |
| 36/35, 128/125, 225/224, 405/392, 729/686, … | August | 399.99 | 107.31 | 3,0 | 5,-1 | 7,0 | 9,-2 | 2.58 | 5.87 | 12, (24d), 33, (36d), 45cd, (48cdd), 57cd, … |
| 50/49, 64/63, 225/224, 2048/2025, … | Pajara | 598.45 | 491.88 | 2,0 | 4,-1 | 3,2 | 4,2 | 3.23 | 3.11 | 22, 32, 34d, (44), 46d, 54, 56d, 58dd, (64bc), … |
| 49/48, 81/80, 245/243, 1323/1280, … | Semaphore | 1203.67 | 252.48 | 1,0 | 2,-2 | 4,-8 | 3,-1 | 3.48 | 3.67 | 19, 33cd, (38d), 43d, 52cd, (57dd), 62dd, … |
| 81/80, 126/125, 225/224, 3136/3125, … | Meantone | 1201.70 | 504.13 | 1,0 | 2,-1 | 4,-4 | 7,-10 | 3.65 | 1.70 | 19, 31, (38d), 43, 50, 55d, (57dd), (62), 67d, … |
| 50/49, 81/80, 405/392, 4000/3969, … | Injera | 600.89 | 507.28 | 2,0 | 4,-1 | 8,-4 | 9,-4 | 3.70 | 3.58 | 26, 38, 50d, (52c), 62d, 64c, 66bcc, 74dd, … |
| 49/48, 225/224, 525/512, 686/675, … | Negri | 1203.19 | 1078.35 | 1,0 | -2,4 | 5,-3 | 1,2 | 3.76 | 3.19 | 19, 29, (38d), 47d, 48d, (57dd), (58cd), … |
| 64/63, 126/125, 128/125, 4000/3969, … | Augene | 399.02 | 90.59* | 3,0 | 5,-1 | 7,0 | 8,2 | 3.76 | 2.94 | 27, 39d, 42, 51cd, (54c), 57bc, 63cdd, 66cd, … |
| 49/48, 126/125, 875/864, 1029/1000, … | Keemun | 1203.19 | 317.84 | 1,0 | 0,6 | 1,5 | 2,3 | 3.85 | 3.19 | 19, 34, (38d), 53d, (57dd), 61bcdd, (68d), … |
| 81/80, 128/125, 648/625, 2048/2025, … | Catler | 99.81 | 75.22 | 12,0 | 19,0 | 28,0 | 33,1 | 3.98 | 3.56 | 36, 48c, 60cd, 60c, 72cd, (72c), 84cdd, 84c, … |
| 50/49, 245/243, 250/243, 2430/2401, … | Hedgehog | 598.45 | 436.13 | 2,0 | 1,3 | 1,5 | 2,5 | 4.09 | 3.11 | 22, 36c, (44), 52bdd, 58c, (66d), (72cc), … |
| 64/63, 245/243, 1728/1715, 2240/2187, … | Superpyth | 1197.60 | 708.17 | 1,0 | 1,1 | -3,9 | 4,-2 | 4.48 | 2.40 | 22, 27, (44), 49, (54c), (66d), 71d, 76bcd, … |
| 126/125, 245/243, 686/675, 4375/4374, … | Sensi | 1198.39 | 755.23 | 1,0 | 6,-7 | 8,-9 | 11,-13 | 4.49 | 1.61 | 19, 27, (38d), 46, (54c), (57dd), 65, 73, 76dd, … |
| 50/49, 525/512, 1029/1024, 1875/1792, … | Lemba | 601.70 | 230.87 | 2,0 | 2,3 | 5,-1 | 6,-1 | 4.54 | 3.74 | 26, (52c), 62c, (78bcc), 88cc, 104bcc, … |
| 64/63, 250/243, 875/864, 6144/6125, … | Porcupine | 1196.91 | 1034.59 | 1,0 | -1,3 | -2,5 | 8,-6 | 4.59 | 3.09 | 22, 37, (44), 59, (66d), (74b), 81bd, (88bd), … |
| 81/80, 525/512, 875/864, 4375/4374, … | Flattone | 1202.54 | 507.14 | 1,0 | 2,-1 | 4,-4 | -1,9 | 4.77 | 2.54 | 26, 45, (52c), 64cd, 71bc, (78bcc), 83bcdd, … |
| 225/224, 245/243, 875/864, 3125/3072, … | Magic | 1201.28 | 380.80 | 1,0 | 0,5 | 2,1 | -1,12 | 4.82 | 1.28 | 22, 41, (44), 60, 63, (66d), 79d, (82), 85, … |
| 50/49, 875/864, 1728/1715, 3125/3024, … | Doublewide | 599.28 | 326.96 | 2,0 | 1,4 | 3,3 | 4,3 | 4.84 | 3.27 | 22, (44), 48, (66d), 70c, 74c, (88bd), 92cd, … |
| 49/48, 250/243, 4000/3969, 6125/5832, … | Nautilus | 1202.99 | 1119.69 | 1,0 | -4,6 | -7,10 | 0,3 | 4.85 | 3.48 | 29, (58cd), (87ccdd), (116ccddd), … |
| 64/63, 686/675, 2401/2400, 6272/6075, … | Beatles | 1197.10 | 842.38 | 1,0 | 3,-2 | -4,9 | 0,4 | 5.24 | 2.90 | 27, (54c), (81bcd), (108bccd), 118bccd, … |
| 81/80, 686/675, 1029/1000, 10976/10935, … | Liese | 1202.62 | 569.05 | 1,0 | 3,-3 | 8,-12 | 8,-11 | 5.43 | 2.62 | [almost 19], 74d, 93dd, 112bdd, 129dd, … |
| 81/80, 1029/1024, 1728/1715, 8748/8575, … | Cynder | 1201.7 | 969.18 | 1,0 | 4,-3 | 12,-12 | 2,1 | 5.72 | 1.70 | 31, 57, (62), 88, (93), 98, (114bc), 119b, … |
| 225/224, 1728/1715, 2430/2401, 6144/6125, … | Orwell | 1199.53 | 271.49 | 1,0 | 0,7 | 3,-3 | 1,8 | 6.20 | 0.95 | 31, 53, (62), 75, 84, (93), (106), 115, (124b), … |
| 225/224, 3125/3087, 4000/3969, 5120/5103, … | Garibaldi | 1200.76 | 702.64 | 1,0 | 1,1 | 7,-8 | 11,-14 | 6.30 | 0.91 | 41, 53, (82), 94, (106), 118d, (123c), 135, 147, … |
| 126/125, 1728/1715, 2401/2400, 31104/30625, … | Myna | 1198.83 | 888.94 | 1,0 | 9,-10 | 9,-9 | 8,-7 | 6.31 | 1.17 | 58, 89, (116c), 120, 143cd, 147c, 151, 174cd, … |
| 225/224, 1029/1024, 2401/2400, 16875/16807, … | Miracle | 1200.63 | 116.72 | 1,0 | 1,6 | 3,-7 | 3,-2 | 6.55 | 0.63 | 41, 72, (82), 103, 113, (123c), 134, (144), … |
| A BONUS TEMPERAMENT: | ||||||||||
| 2401/2400, 4375/4374, 250047/250000, … | Ennealimmal | 133.337 | 84.313 | 9,0 | 13,2 | 19,3 | 24,2 | 12.36 | 0.04 | |
∗ Correction from the Xenharmonikon version, which gives the corner case generator 92.46 erroneously.
| ET | TOP damage | TOP octave | Rank-2 temperaments supported |
|---|---|---|---|
| 12 | Diminished, dominant, august | ||
| 15 | Blacksmith | ||
| 19 | Semaphore, meantone, negri, keemun, sensi | ||
| 22 | Pajara, hedgehog, superpyth, porcupine, magic, doublewide | ||
| 24d* | Diminished, dominant, august | ||
| 25 | Blacksmith | ||
| 26 | Injera, lemba, flattone | ||
| 27 | Augene, superpyth, sensi, beatles | ||
| 29 | Negri, nautilus | ||
| 29cd | Dominant | ||
| 30* | Blacksmith | ||
| 31 | Meantone, cynder, orwell | ||
| 32 | Pajara | ||
| 33 | August | ||
| 33cd | Semaphore | ||
| 34 | Keemun | ||
| 34d | Pajara | ||
| 35bc | Blacksmith | ||
| 36 | Catler | ||
| 36c | Hedgehog | ||
| 36d* | Diminished, dominant, august | ||
| 37 | Porcupine | ||
| 38 | Injera | ||
| 38d* | Semaphore, meantone, negri, keemun, sensi | ||
| 39d | Augene | ||
| 40b | Blacksmith | ||
| 41 | Magic, garibaldi, miracle | ||
| 41cd | Dominant | ||
| 42 | Augene | ||
| 43 | Meantone | ||
| 43d | Semaphore | ||
| 44* | Pajara, hedgehog, superpyth, porcupine, magic, doublewide | ||
| 45 | Flattone | ||
| 45bc | Blacksmith | ||
| 45cd | August | ||
| 46 | Sensi | ||
| 46ccd | Dominant | ||
| 46d | Pajara | ||
| 47d | Negri | ||
| 48 | Doublewide | ||
| 48c | Catler | ||
| 48cdd* | Diminished, dominant, august | ||
| 48d | Negri | ||
| 49 | Superpyth | ||
| 50 | Meantone | ||
| 50b* | Blacksmith | ||
| 50bc | Blacksmith | ||
| 50d | Injera | ||
| 51cd | Augene | ||
| 52bdd | Hedgehog | ||
| 52c* | Injera, lemba, flattone | ||
| 52cd | Semaphore | ||
| 53 | Orwell, garibaldi | ||
| 53cdd | Dominant | ||
| 53d | Keemun | ||
| 54 | Pajara | ||
| 54c* | Augene, superpyth, sensi, beatles | ||
| 55b | Blacksmith | ||
| 55d | Meantone | ||
| 56cddd | Diminished | ||
| 56d | Pajara | ||
| 57 | Cynder | ||
| 57bc | Augene | ||
| 57cd | August | ||
| 57dd* | Semaphore, meantone, negri, keemun, sensi | ||
| 58 | Myna | ||
| 58c | Hedgehog | ||
| 58ccdd* | Dominant | ||
| 58cd* | Negri, nautilus | ||
| 58dd | Pajara | ||
| 59 | Porcupine | ||
| 60 | Magic | ||
| 60b | Blacksmith | ||
| 60bc* | Blacksmith | ||
| 60c | Catler | ||
| 60cd | Catler | ||
| 60cddd* | Diminished, dominant, august |
* contorted
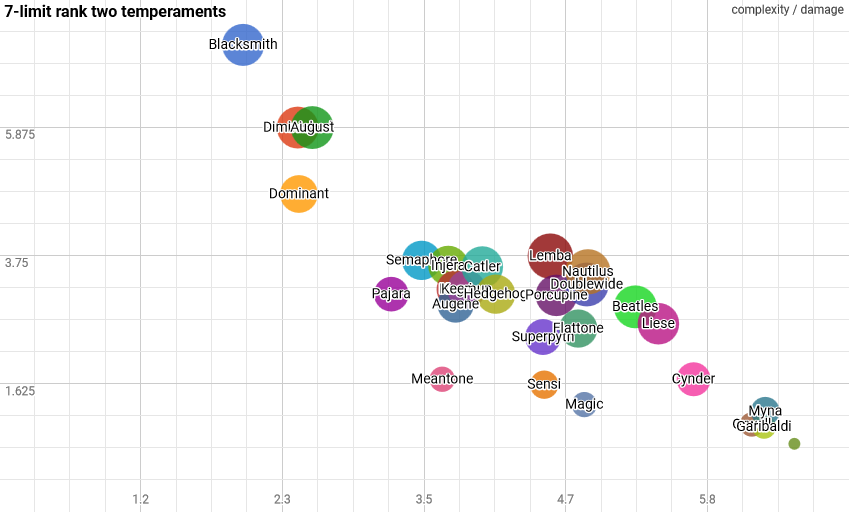
The bubble chart above (source) arranges the temperaments by complexity (x-axis) vs. damage (y-axis). Colors are arbitrary. The size of the bubble is proportional to (complexity × damage). Note that the "bonus temperament" ennealimmal is not shown (a much larger range would be needed to make it visible).
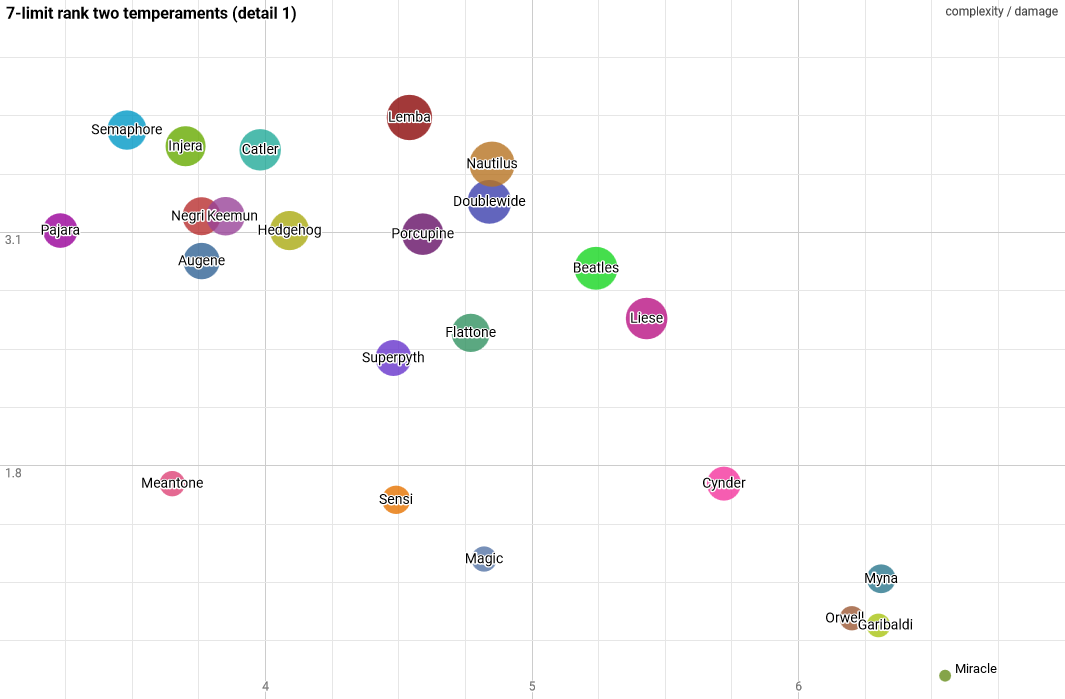
The same chart, only "zoomed in".