Middle Path table of five-limit rank two temperaments
This table is an an updated version of Table 1 of Paul Erlich's A Middle Path. The complexity is now measured a different way (which, however, is proportional to the original complexity for this table), and some temperament names have been updated.
The "main sequence" of this table comprises all possible five-limit 2-D cases where complexity/7.65 + damage/10 < 1. The 'exotemperaments' have larger damage and lend themselves to special measures such as custom inharmonic timbres in order to aid harmoniousness. The 'bonus temperaments' are more complex but have exceedingly small damage and sound like JI.
See also Middle Path table of seven-limit rank two temperaments, Middle Path table of eleven-limit rank two temperaments.
| Vanishing Interval's Ratio | V.I. Vector | V.I. cents | Temperament name |
TOP period |
TOP generator |
Mapp. of 2 |
Mapp. of 3 |
Mapp. of 5 |
Cmplx. | TOP Dmg. |
ETs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TWO EXOTEMPERAMENTS: | |||||||||||
| 16/15 | [4, -1, -1> | 111.7 | Father | 1185.9 | 447.4 | 1, 0 | 2, -1 | 2, 1 | 1.37 | 14.13 | |
| 27/25 | [0, 3, -2> | 133.2 | Bug | 1200.0 | 260.3 | 1, 0 | 2, -2 | 3, -3 | 1.63 | 14.18 | |
| MAIN SEQUENCE: | |||||||||||
| 25/24 | [-3, -1, 2> | 70.7 | Dicot | 1207.66 | 353.22 | 1, 0 | 1, 2 | 2, 1 | 1.60 | 7.66 | 24c, 41cc, (48cc), 65ccc... |
| 81/80 | [-4, 4, -1> | 21.5 | Meantone | 1201.70 | 504.13 | 1, 0 | 2, -1 | 4, -4 | 2.19 | 1.70 | 12, 19, (24), 26, 29c, 31, 33c, (36)... |
| 128/125 | [7, 0, -3> | 41.1 | Augmented | 399.02 | 93.15 | 3, 0 | 5, -1 | 7, 0 | 2.42 | 2.94 | 12, 15, (24), 27, (30), 33, (36), 39... |
| 135/128 | [-7, 3, 1> | 92.2 | Mavila | 1206.55 | 685.03 | 1, 0 | 1, 1 | 4, -3 | 2.44 | 6.55 | 37bc, 67bbccc, (74bbccc), 81bbcccc... |
| 250/243 | [1, -5, 3> | 49.2 | Porcupine | 1196.91 | 1034.59 | 1, 0 | -1, 3 | -2, 5 | 2.75 | 3.09 | 15, 22, 29, (30), 36c, 37, 43c, (44)... |
| 256/243 | [8, -5, 0> | 90.2 | Blackwood | 238.87 | 158.78 | 5, 0 | 8, 0 | 11, 1 | 2.76 | 5.67 | 15, 25, (30), 35bc, 40b, (45bc)... |
| 648/625 | [3, 4, -4> | 62.6 | Diminished | 299.16 | 197.49 | 4, 0 | 7, -1 | 10, -1 | 3.23 | 3.36 | 12, (24), 28, 32c, (36), 40, 44c, (48c)... |
| 2048/2025 | [11, -4, -2> | 19.6 | Srutal | 599.56 | 494.86 | 2, 0 | 4, -1 | 3, 2 | 3.81 | 0.89 | 12, 22, (24), 34, (36), (44), 46, (48c), 54... |
| 3125/3072 | [-10, -1, 5> | 29.6 | Magic | 1201.28 | 380.80 | 1, 0 | 0, 5 | 2, 1 | 4.02 | 1.28 | 19, 22, (38), 41, (44), 54b, (57), 60... |
| 6561/6250 | [-1, 8, -5> | 84.1 | Ripple | 1203.32 | 101.99 | 1, 0 | 2, -5 | 3, -8 | 4.38 | 3.32 | 12, (24), (36), 47, (48c), 59b, (60c)... |
| 15625/15552 | [-6, -5, 6> | 8.11 | Hanson | 1200.29 | 317.07 | 1, 0 | 0, 6 | 1, 5 | 4.83 | 0.29 | 19, 34, (38), 49, 53, (57), 64b, (68)... |
| 16875/16384 | [-14, 3, 4> | 51.1 | Negri | 1201.82 | 1075.68 | 1, 0 | -2, 4 | 5, -3 | 4.86 | 1.82 | 19, 29, (38), 48, (57), (58c), 66b, 67c... |
| 20000/19683 | [5, -9, 4> | 27.7 | Tetracot | 1199.03 | 176.11 | 1, 0 | 1, 4 | 1, 9 | 4.95 | 0.97 | 27, 34, 41, 48, (54c), 55c, 61, (68), 75... |
| 20480/19683 | [12, -9, 1> | 68.7 | Superpyth | 1197.60 | 708.17 | 1, 0 | 1, 1 | -3, 9 | 4.95 | 2.40 | 22, 27, (44), 49, (54c), (66), 71, 76bc... |
| 32805/32768 | [-15, 8, 1> | 1.95 | Helmholtz | 1200.07 | 701.79 | 1, 0 | 1, 1 | 7, -8 | 5.20 | 0.07 | 41, 53, 65, 70c, 77, (82), 89, 94, 99c... |
| 78732/78125 | [2, 9, -7> | 13.4 | Sensi | 1199.59 | 756.60 | 1, 0 | 6, -7 | 8, -9 | 5.63 | 0.41 | 19, (38), 46, (57), 65, 73, (76), 84... |
| 262144/253125 | [18, -4, -5> | 60.6 | Passion | 1198.31 | 98.40 | 1, 0 | 2, -5 | 2, 4 | 6.23 | 1.69 | 73, 134bc, (146bc), 158bcc... |
| 393216/390625 | [17, 1, -8> | 11.4 | Würschmidt | 1199.69 | 812.05 | 1, 0 | 7, -8 | 3, -1 | 6.44 | 0.31 | 34, 65, (68), 96, 99, (102)... |
| 531441/524288 | [-19, 12, 0> | 23.5 | Compton | 100.05 | 15.13 | 12, 0 | 19, 0 | 28, -1 | 6.59 | 0.62 | 60, 72, 84, 96, 108, (120c), 132... |
| 1600000/1594323 | [9, -13, 5> | 6.15 | Amity | 1199.85 | 860.38 | 1, 0 | -2, 5 | -7, 13 | 7.14 | 0.15 | 53, 99, (106), 145, 152, (159)... |
| 2109375/2097152 | [-21, 3, 7> | 10.1 | Orson | 1200.24 | 271.65 | 1, 0 | 0, 7 | 3, -3 | 7.28 | 0.24 | 53, (106), 137, (159), 190... |
| TWO BONUS TEMPERAMENTS: | |||||||||||
| 6115295232/6103515625 | [23, 6, -14> | 3.34 | Vishnu | 599.97 | 71.15 | 2, 0 | 4, -7 | 5, -3 | 11.27 | 0.05 | |
| 274877906944/274658203125 | [38, -2, -15> | 1.38 | Luna | 1199.98 | 193.196 | 1, 0 | 4, -15 | 2, 2 | 13.17 | 0.02 | |
| ET | TOP damage | TOP octave | Rank-2 temperaments supported |
|---|---|---|---|
| 12 | 3.56 | 1197.67 | meantone, augmented, diminished, srutal, ripple |
| 15 | 5.67 | 1194.33 | augmented, porcupine, blackwood |
| 19 | 2.28 | 1202.28 | meantone, magic, hanson, negri, sensi |
| 22 | 3.22 | 1198.72 | porcupine, srutal, magic, superpyth |
| 24 (contorted) | 3.56 | 1197.67 | meantone, augmented, diminished, srutal, ripple |
| 24c | 7.87 | 1207.87 | dicot |
| 25 | 6.16 | 1194.83 | blackwood |
| 26 | 3.69 | 1203.69 | meantone |
| 27 | 2.94 | 1197.06 | augmented, tetracot, superpyth |
| 28 | 5.15 | 1205.15 | diminished |
| 29 | 3.47 | 1202.53 | porcupine, negri |
| 29c | 5.89 | 1194.11 | meantone |
| 30 (contorted) | 5.67 | 1194.33 | augmented, porcupine, blackwood |
| 31 | 1.81 | 1201.47 | meantone |
| 32c | 5.61 | 1194.39 | diminished |
| 33 | 6.43 | 1200.54 | augmented |
| 33c | 4.90 | 1204.90 | meantone |
| 34 | 1.24 | 1198.76 | srutal, hanson, tetracot, wuerschmidt |
| 35bc | 9.43 | 1209.43 | blackwood |
| 36 (contorted) | 3.56 | 1197.67 | meantone, augmented, diminished, srutal, ripple |
| 36c | 4.25 | 1204.25 | porcupine |
| 37 | 3.64 | 1196.36 | porcupine |
| 37bc | 6.62 | 1206.62 | mavila |
| 38 (contorted) | 2.28 | 1202.28 | meantone, magic, hanson, negri, sensi |
|
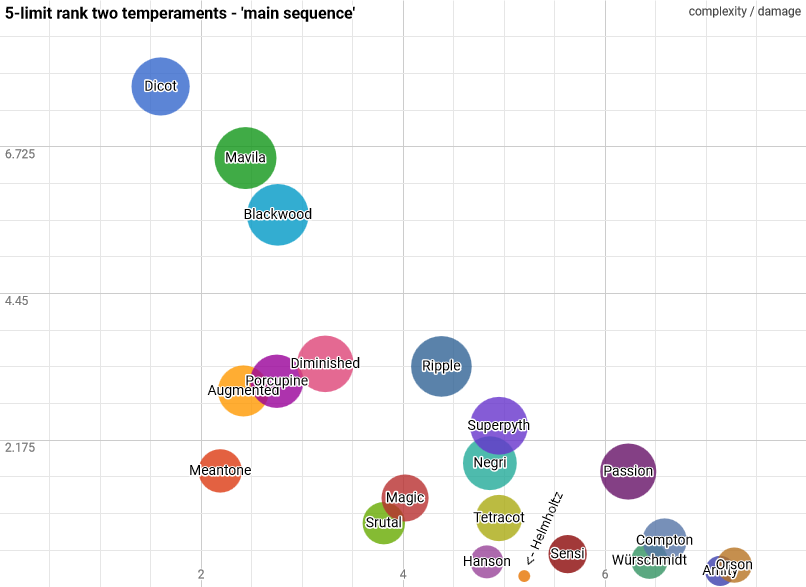
The bubble chart above (source) arranges the temperaments by complexity (x-axis) vs. damage (y-axis). Colors are arbitrary. The size of the bubble is proportional to the size of the comma (vanishing interval). Note that the "exotemperaments" and "bonus temperaments" are not shown (a much larger range is needed to make them visible).