6edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Fredg999 (talk | contribs)
autopatrolled, Interface administrators, Sysops
6,129 edits
m →Music: Misc. edits (details include lyrics, to simplify)
Yourmusic Productions (talk | contribs)
autopatrolled, emailconfirmed
891 edits
→Instruments: expansion.
 
(25 intermediate revisions by 11 users not shown)
Line 5: Line 5:
| ja = 6平均律
| ja = 6平均律
}}
}}
{{Infobox ET}}
{{Wikipedia|Whole tone scale}}
{{Wikipedia|Whole tone scale}}
'''6 equal divisions of the octave''' ('''6edo''') is the [[tuning system]] derived by dividing the [[octave]] into 6 equal steps of 200 [[cent]]s each, or the sixth root of 2. It is also known as the '''whole tone scale'''.  
{{ED intro}} It is also known as the '''whole tone scale'''.  


== Theory ==
== Theory ==
{{Harmonics in equal|6|intervals=odd}}
6edo is identical to the 12edo whole-tone scale, however, it does have xenharmonic theoretical appeal. The 6-form is a simple basis for harmony in the [[2.5.7 subgroup]], somewhat like the [[Heptatonic|7-form]] for 2.3.5 and the [[Pentatonic|5-form]] for 2.3.7. This means that 6edo itself can be seen as a particularly crude tuning of temperaments like [[didacus]], in the same way as 7edo for [[meantone]] or 5edo for [[superpyth]]. The root chord in this harmonic system can be seen as:
 
* [0 2 5] = 4:5:7, with the harmonic seventh as a bounding interval
* [0 3 4] = 5:7:8, with the minor sixth as a bounding interval
* [0 1 3] = 7:8:10, with the large septimal tritone as a bounding interval
 
Whichever way, this is very different from standard functional harmony.
 
If the prime 3 is added, it leads to absurd interpretations such as [[father]], as it is almost 100 cents sharp. However, in a composite subgroup, the 9th harmonic can be introduced, being directly approximated by 1 step of 6edo. In 2.9.5.7, the most salient fact about 6edo is that both [[64/63]] and [[81/80]] are tempered out, implying the restriction of both 2.3.7 [[superpyth]] and 2.3.5 [[meantone]] temperament (that is, [[Dominant (temperament)|dominant]] temperament) to 2.9.5.7.


As a subset of [[12edo]], 6edo can be notated on a five-line staff with standard notation. It is the first [[edo]] that is not a [[The Riemann zeta function and tuning #Zeta edo lists|zeta peak]], has lower [[Consistency limits of small EDOs|consistency]] than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12 tone instrument.
6edo is the first edo to have lower [[Consistency limits of small EDOs|consistency]] than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.


While 6edo does not well approximate the 3rd harmonic, it does contain a good approximation of the 9th harmonic. Therefore, 6edo can be treated as a 2.5.7.9 subgroup temperament.
=== Notation ===
As a subset of [[12edo]], 6edo can be notated on a five-line staff with standard notation.  


Related edos:
=== Odd harmonics ===
* Subsets: [[2edo]], [[3edo]]
{{Harmonics in equal|6|intervals=odd}}
 
=== Subsets and supersets ===
* Subsets: [[2edo]] and [[3edo]]
* Supersets: [[12edo]], [[18edo]], [[24edo]] …
* Supersets: [[12edo]], [[18edo]], [[24edo]] …
* Neighbours: [[5edo]], [[7edo]]


== Intervals ==
== Intervals ==
{| class="wikitable right-1 right-2"
{| class="wikitable center-all"
! Steps
|+ style="font-size: 105%;" | Intervals of 6edo
! Cents
|-
! colspan="3" | Interval
! rowspan="2" | [[Degree]]
! Approximate JI Ratios*
! rowspan="2" | [[Cent]]s
! rowspan="2" | [[Interval region]]
! colspan="4" | Approximated [[JI]] intervals<ref group="note">{{sg|limit=subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup}} For example, for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).</ref>
! rowspan="2" | Audio
|-
! [[3-limit]]
! [[5-limit]]
! [[7-limit]]
! Other
|-
| 0
| 0
| Unison (prime)
| [[1/1]] (just)
|
|
|
| [[File:piano_0_1edo.mp3]]
|-
| 1
| 200
| Major second
| [[9/8]] (−3.910)
| [[10/9]] (+17.596)
| [[28/25]] (+3.802)<br />[[8/7]] (−31.174)
| [[19/17]] (+7.442)<br />[[55/49]] (+0.020)<br />[[64/57]] (−0.532)<br />[[17/15]] (−16.687)
| [[File:piano_1_6edo.mp3]]
|-
| 2
| 400
| Major third
| [[81/64]] (−7.820)
| [[5/4]] (+13.686)
| [[63/50]] (−0.108)<br />[[9/7]] (−35.084)
| [[34/27]] (+0.910)
| [[File:piano_1_3edo.mp3]]
|-
| 3
| 600
| [[Tritone]]
|
|
| [[7/5]] (+17.488)<br />[[10/7]] (−17.488)
| [[24/17]] (+3.000)<br />[[99/70]] (−0.088)<br />[[17/12]] (−3.000)
| [[File:piano_1_2edo.mp3]]
|-
| 4
| 800
| Minor sixth
| [[128/81]] (+7.820)
| [[8/5]] (−13.686)
| [[14/9]] (+35.084)<br />[[100/63]] (+0.108)
| [[27/17]] (−0.910)
| [[File:piano_2_3edo.mp3]]
|-
| 5
| 1000
| Minor seventh
| [[16/9]] (+3.910)
| [[9/5]] (−17.596)
| [[7/4]] (+31.174)<br />[[25/14]] (−3.802)
| [[30/17]] (+16.687)<br />[[57/32]] (+0.532)<br />[[98/55]] (−0.020)<br />[[34/19]] (−7.442)
| [[File:piano_5_6edo.mp3]]
|-
| 6
| 1200
| Octave
| [[2/1]] (just)
|
|
|
| [[File:piano_1_1edo.mp3]]
|}
 
== Notation ==
{| class="wikitable center-all"
|+ style="font-size: 105%;" | Notation of 6edo
|-
! rowspan="2" | [[Degree]]
! rowspan="2" | [[Cent]]s
! colspan="2" | [[12edo]] [[subset notation]]
|-
! [[5L 2s|Diatonic]] interval names
! Note names (on D)
|-
| 0
| 0
| '''Perfect unison (P1)'''
| '''D'''
|-
| 1
| 200
| '''Major second (M2)'''<br />Diminished third (d3)
| '''E'''<br />Fb
|-
| 2
| 400
| Major third (M3)<br />Diminished fourth (d4)
| F#<br />Gb
|-
| 3
| 600
| Augmented fourth (A4)<br />Diminished fifth (d5)
| G#<br />Ab
|-
| 4
| 800
| Augmented fifth (A5)<br />Minor sixth (m6)
| A#<br />Bb
|-
| 5
| 1000
| Augmented sixth (A6)<br />'''Minor seventh (m7)'''
| B#<br />'''C'''
|-
| 6
| 1200
| '''Perfect octave (P8)'''
| '''D'''
|}
 
In 6edo:
* [[ups and downs notation]] is identical to standard notation;
* mixed [[sagittal notation]] is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp ([[File:Sagittal sharp.png]]) and sagittal flat ([[File:Sagittal flat.png]]) respectively.
 
=== Sagittal notation ===
This notation is a subset of the notations for EDOs [[12edo#Sagittal notation|12]], [[18edo#Sagittal notation|18]], [[24edo#Sagittal notation|24]], [[36edo#Sagittal notation|36]], [[48edo#Sagittal notation|48]], [[60edo#Sagittal notation|60]], [[72edo#Sagittal notation|72]], and [[84edo#Sagittal notation|84]].
 
==== Evo flavor ====
<imagemap>
File:6-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 368 0 528 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 368 106 [[12-EDO#Sagittal_notation| 12-EDO notation]]
default [[File:6-EDO_Evo_Sagittal.svg]]
</imagemap>
 
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
 
==== Revo flavor ====
<imagemap>
File:6-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 376 0 536 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 376 106 [[12-EDO#Sagittal_notation | 12-EDO notation]]
default [[File:6-EDO_Revo_Sagittal.svg]]
</imagemap>
 
== Solfege ==
{| class="wikitable center-all"
|+ style="font-size: 105%;" | Solfege of 6edo
|-
! [[Degree]]
! [[Cents]]
! 12edo subset<br />standard [[solfege]]<br />(movable do)
! 12edo subset<br />[[uniform solfege]]<br />(2–3 vowels)
|-
|-
| 0
| 0
| 0
| 0
| unison
| Do
| P1
| Da
| D
| [[1/1]]
|-
|-
| 1
| 1
| 200
| 200
| major 2nd
| Re
| M2
| Ra
| E
| [[8/7]], [[9/8]], [[10/9]]
|-
|-
| 2
| 2
| 400
| 400
| major 3rd
| Mi
| M3
| Ma (M3)<br />Fo (d4)
| F#
| [[5/4]], [[9/7]]
|-
|-
| 3
| 3
| 600
| 600
| aug 4th, dim 5th
| Fi (A4)<br />Se (d5)
| A4, d5
| Pa (A4)<br />Sha (d5)
| G#, Ab
| [[7/5]], [[10/7]]
|-
|-
| 4
| 4
| 800
| 800
| minor 6th
| Si (A5)<br />Le (m6)
| m6
| Su (A5)<br />Fla (m6)
| Bb
| [[8/5]], [[14/9]]
|-
|-
| 5
| 5
| 1000
| 1000
| minor 7th
| Li (A6)<br />Te (m7)
| m7
| Lu (A6)<br />Tha (m7)
| C
| [[7/4]], [[9/5]], [[16/9]]
|-
|-
| 6
| 6
| 1200
| 1200
| perfect 8ve
| Do
| P8
| Da
| D
| [[2/1]]
|}
|}
<nowiki>*</nowiki> based on treating 6edo as a 2.5.7.9 subgroup temperament; other approaches are possible.


== Commas ==
== Regular temperament properties ==
6edo [[tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 6 10 14 17 21 22 }}.  
=== Uniform maps ===
{{Uniform map|edo=6}}
 
=== Commas ===
6et [[tempering out|tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 6 10 14 17 21 22 }}.  


{| class="commatable wikitable center-1 center-2 right-4 center-5"
{| class="commatable wikitable center-1 center-2 right-4 center-5"
|-
|-
! [[Harmonic limit|Prime<br>Limit]]
! [[Harmonic limit|Prime<br />limit]]
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Ratio]]<ref group="note">{{rd}}</ref>
! [[Monzo]]
! [[Monzo]]
! [[Cent]]s
! [[Cent]]s
Line 102: Line 260:
| 70.67
| 70.67
| Yoyo
| Yoyo
| Classic chromatic semitone
| Dicot comma, classic chroma
|-
|-
| 5
| 5
Line 109: Line 267:
| 41.06
| 41.06
| Trigu
| Trigu
| Diesis, augmented comma
| Augmented comma, diesis
|-
|-
| 5
| 5
Line 116: Line 274:
| 29.61
| 29.61
| Laquinyo
| Laquinyo
| Small diesis, magic comma
| Magic comma, small diesis
|-
|-
| 5
| 5
Line 137: Line 295:
| 35.70
| 35.70
| Zozo
| Zozo
| Slendro diesis
| Semaphoresma, slendro diesis
|-
|-
| 7
| 7
Line 144: Line 302:
| 34.98
| 34.98
| Biruyo
| Biruyo
| Tritonic diesis, jubilisma
| Jubilisma, tritonic diesis
|-
|-
| 7
| 7
Line 151: Line 309:
| 6.08
| 6.08
| Zozoquingu
| Zozoquingu
| Hemimean
| Hemimean comma
|-
|-
| 7
| 7
Line 158: Line 316:
| 5.36
| 5.36
| Sarurutrigu
| Sarurutrigu
| Porwell
| Porwell comma
|-
|-
| 7
| 7
Line 195: Line 353:
| Tridecimal neutral second
| Tridecimal neutral second
|}
|}
<references/>
 
== Instruments ==
Any instruments that can play the full gamut of 12edo (ie, not diatonic harmonicas, dulcimers or harps) can obviously also play 6edo as well, although it is significantly more ergonomic on some instruments than others.
 
If you want a more specialist design making 6edo music easy to play without having to worry about hitting out of key 12edo notes, a [[Lumatone mapping for 6edo]] is available, or you could remove all the unwanted bars on a xylophone or marimba.


== Music ==
== Music ==
'''Chimeratio'''
; [[Bryan Deister]]
* "[https://soundcloud.com/sexytoadsandfrogsfriendcircle/6-chimeratio-bowser-breaks Bowser breaks into Arnold Schoenberg's house and steals six of the twelve Tone Crystals (every other one), activating The 666666-Year-Curse Mechanism]", from [https://soundcloud.com/sexytoadsandfrogsfriendcircle/sets/staffcirc-vol-7-terra-octava ''STAFFcirc vol. 7''] (2021) ([https://sexytoadsandfrogsfriendcircle.bandcamp.com/track/6-bowser-breaks-into-arnold-schoenbergs-house-and-steals-six-of-the-twelve-tone-crystals-every-other-one-activating-the-666666-year-curse-mechanism Bandcamp])
* [https://www.youtube.com/watch?v=knvdNFjKj-o ''6edo improvisation''] (2024)
 
; [[Chimeratio]]
* "Bowser breaks into Arnold Schoenberg's house and steals six of the twelve Tone Crystals (every other one), activating The 666666-Year-Curse Mechanism", from [https://soundcloud.com/sexytoadsandfrogsfriendcircle/sets/staffcirc-vol-7-terra-octava ''STAFFcirc vol. 7''] (2021) – [https://soundcloud.com/sexytoadsandfrogsfriendcircle/6-chimeratio-bowser-breaks SoundCloud] | [https://sexytoadsandfrogsfriendcircle.bandcamp.com/track/6-bowser-breaks-into-arnold-schoenbergs-house-and-steals-six-of-the-twelve-tone-crystals-every-other-one-activating-the-666666-year-curse-mechanism Bandcamp]


'''Milan Guštar'''
; [[Milan Guštar]]
* [http://www.uvnitr.cz/flaoyg/forgotten_works/dvandva.html "Dvandva"] (1987/2007)
* [http://www.uvnitr.cz/flaoyg/forgotten_works/dvandva.html ''Dvandva''] (1987/2007)


'''[[Aaron Andrew Hunt]]'''
; [[Aaron Andrew Hunt]]
* "[https://aaronandrewhunt.bandcamp.com/track/prelude-in-6et Prelude in 6ET]", from ''[https://aaronandrewhunt.bandcamp.com/album/the-equal-tempered-keyboard The Equal-Tempered Keyboard]'' (1999-2022) ([https://soundcloud.com/uz1kt3k/prelude-in-6et SoundCloud])
* From [https://aaronandrewhunt.bandcamp.com/album/the-equal-tempered-keyboard ''The Equal-Tempered Keyboard''] (1999–2022)
* "[https://aaronandrewhunt.bandcamp.com/track/invention-in-6et Invention in 6ET]", from ''The Equal-Tempered Keyboard'' (1999-2022) ([https://soundcloud.com/uz1kt3k/invention-in-6et SoundCloud])
** "Prelude in 6ET" – [https://aaronandrewhunt.bandcamp.com/track/prelude-in-6et Bandcamp] | [https://soundcloud.com/uz1kt3k/prelude-in-6et SoundCloud]{{dead link}}
** "Invention in 6ET" – [https://aaronandrewhunt.bandcamp.com/track/invention-in-6et Bandcamp] | [https://soundcloud.com/uz1kt3k/invention-in-6et SoundCloud]{{dead link}}


'''NullPointerException Music'''
; [[NullPointerException Music]]
* [https://www.youtube.com/watch?v=AleKBhXifzY "Exiting"], from [https://www.youtube.com/playlist?list=PLg1YtcJbLxnwTJkG4m0BWZWxIHj7ScdNn ''Edolian''] (2020)
* [https://www.youtube.com/watch?v=AleKBhXifzY "Exiting"], from [https://www.youtube.com/playlist?list=PLg1YtcJbLxnwTJkG4m0BWZWxIHj7ScdNn ''Edolian''] (2020)


'''[[Chris Vaisvil]]'''
; [[User:Phanomium|Phanomium]]
* [http://micro.soonlabel.com/6edo/the-good-boundless-03.mp3 ''The Good Boundless''] (2011) ([http://chrisvaisvil.com/the-good-boundless/ details])
* [https://www.youtube.com/watch?v=6V97NrhUaps ''Heximal''] (2024)
 
; [[Chris Vaisvil]]
* ''The Good Boundless'' (2011) – [https://www.chrisvaisvil.com/the-good-boundless/ blog] | [https://web.archive.org/web/20230530111053/http://micro.soonlabel.com/6edo/the-good-boundless-03.mp3 play]
 
== Notes ==
<references group="note" />


[[Category:6edo| ]] <!-- main article -->
[[Category:Equal divisions of the octave|#]] <!-- 1-digit number -->
[[Category:6-tone scales]]
[[Category:6-tone scales]]
[[Category:Listen]]
[[Category:Listen]]
[[Category:Macrotonal]]
[[Category:Subgroup]]

Latest revision as of 09:37, 6 August 2025

← 5edo 6edo 7edo →
Prime factorization 2 × 3
Step size 200 ¢ 
Fifth 4\6 (800 ¢) (→ 2\3)
Semitones (A1:m2) 4:-2 (800 ¢ : -400 ¢)
Dual sharp fifth 4\6 (800 ¢) (→ 2\3)
Dual flat fifth 3\6 (600 ¢) (→ 1\2)
Dual major 2nd 1\6 (200 ¢)
(convergent)
Consistency limit 7
Distinct consistency limit 3
Special properties
English Wikipedia has an article on:

6 equal divisions of the octave (abbreviated 6edo or 6ed2), also called 6-tone equal temperament (6tet) or 6 equal temperament (6et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 6 equal parts of exactly 200 ¢ each. Each step represents a frequency ratio of 21/6, or the 6th root of 2. It is also known as the whole tone scale.

Theory

6edo is identical to the 12edo whole-tone scale, however, it does have xenharmonic theoretical appeal. The 6-form is a simple basis for harmony in the 2.5.7 subgroup, somewhat like the 7-form for 2.3.5 and the 5-form for 2.3.7. This means that 6edo itself can be seen as a particularly crude tuning of temperaments like didacus, in the same way as 7edo for meantone or 5edo for superpyth. The root chord in this harmonic system can be seen as:

  • [0 2 5] = 4:5:7, with the harmonic seventh as a bounding interval
  • [0 3 4] = 5:7:8, with the minor sixth as a bounding interval
  • [0 1 3] = 7:8:10, with the large septimal tritone as a bounding interval

Whichever way, this is very different from standard functional harmony.

If the prime 3 is added, it leads to absurd interpretations such as father, as it is almost 100 cents sharp. However, in a composite subgroup, the 9th harmonic can be introduced, being directly approximated by 1 step of 6edo. In 2.9.5.7, the most salient fact about 6edo is that both 64/63 and 81/80 are tempered out, implying the restriction of both 2.3.7 superpyth and 2.3.5 meantone temperament (that is, dominant temperament) to 2.9.5.7.

6edo is the first edo to have lower consistency than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.

Notation

As a subset of 12edo, 6edo can be notated on a five-line staff with standard notation.

Odd harmonics

Approximation of odd harmonics in 6edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +98.0 +13.7 +31.2 -3.9 +48.7 -40.5 -88.3 +95.0 -97.5 -70.8 -28.3
Relative (%) +49.0 +6.8 +15.6 -2.0 +24.3 -20.3 -44.1 +47.5 -48.8 -35.4 -14.1
Steps
(reduced) 		10
(4) 		14
(2) 		17
(5) 		19
(1) 		21
(3) 		22
(4) 		23
(5) 		25
(1) 		25
(1) 		26
(2) 		27
(3)

Subsets and supersets

Intervals

Intervals of 6edo
Degree Cents Interval region Approximated JI intervals[note 1] Audio
3-limit 5-limit 7-limit Other
0 0 Unison (prime) 1/1 (just)
1 200 Major second 9/8 (−3.910) 10/9 (+17.596) 28/25 (+3.802)
8/7 (−31.174) 		19/17 (+7.442)
55/49 (+0.020)
64/57 (−0.532)
17/15 (−16.687)
2 400 Major third 81/64 (−7.820) 5/4 (+13.686) 63/50 (−0.108)
9/7 (−35.084) 		34/27 (+0.910)
3 600 Tritone 7/5 (+17.488)
10/7 (−17.488) 		24/17 (+3.000)
99/70 (−0.088)
17/12 (−3.000)
4 800 Minor sixth 128/81 (+7.820) 8/5 (−13.686) 14/9 (+35.084)
100/63 (+0.108) 		27/17 (−0.910)
5 1000 Minor seventh 16/9 (+3.910) 9/5 (−17.596) 7/4 (+31.174)
25/14 (−3.802) 		30/17 (+16.687)
57/32 (+0.532)
98/55 (−0.020)
34/19 (−7.442)
6 1200 Octave 2/1 (just)

Notation

Notation of 6edo
Degree Cents 12edo subset notation
Diatonic interval names Note names (on D)
0 0 Perfect unison (P1) D
1 200 Major second (M2)
Diminished third (d3) 		E
Fb
2 400 Major third (M3)
Diminished fourth (d4) 		F#
Gb
3 600 Augmented fourth (A4)
Diminished fifth (d5) 		G#
Ab
4 800 Augmented fifth (A5)
Minor sixth (m6) 		A#
Bb
5 1000 Augmented sixth (A6)
Minor seventh (m7) 		B#
C
6 1200 Perfect octave (P8) D

In 6edo:

  • ups and downs notation is identical to standard notation;
  • mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp (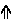) and sagittal flat (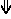) respectively.

Sagittal notation

This notation is a subset of the notations for EDOs 12, 18, 24, 36, 48, 60, 72, and 84.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation12-EDO notation

Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation12-EDO notation

Solfege

Solfege of 6edo
Degree Cents 12edo subset
standard solfege
(movable do) 		12edo subset
uniform solfege
(2–3 vowels)
0 0 Do Da
1 200 Re Ra
2 400 Mi Ma (M3)
Fo (d4)
3 600 Fi (A4)
Se (d5) 		Pa (A4)
Sha (d5)
4 800 Si (A5)
Le (m6) 		Su (A5)
Fla (m6)
5 1000 Li (A6)
Te (m7) 		Lu (A6)
Tha (m7)
6 1200 Do Da

Regular temperament properties

Uniform maps

13-limit uniform maps between 5.8 and 6.2
Min. size Max. size Wart notation Map
5.6368 5.8101 6bcdeff ⟨6 9 13 16 20 21]
5.8101 5.8141 6bcde ⟨6 9 13 16 20 22]
5.8141 5.8774 6bde ⟨6 9 14 16 20 22]
5.8774 5.9258 6be ⟨6 9 14 17 20 22]
5.9258 5.9938 6b ⟨6 9 14 17 21 22]
5.9938 6.0804 6 ⟨6 10 14 17 21 22]
6.0804 6.2149 6f ⟨6 10 14 17 21 23]

Commas

6et tempers out the following commas. This assumes val ⟨6 10 14 17 21 22].

Prime
limit 		Ratio[note 2] Monzo Cents Color name Name(s)
3 32/27 [5 -3⟩ 294.13 Wa Pythagorean minor third
5 25/24 [-3 -1 2⟩ 70.67 Yoyo Dicot comma, classic chroma
5 128/125 [7 0 -3⟩ 41.06 Trigu Augmented comma, diesis
5 3125/3072 [-10 -1 5⟩ 29.61 Laquinyo Magic comma, small diesis
5 (12 digits) [17 1 -8⟩ 11.45 Saquadbigu Würschmidt comma
5 (30 digits) [-44 -3 21⟩ 6.72 Trila-septriyo Mutt comma
7 49/48 [-4 -1 0 2⟩ 35.70 Zozo Semaphoresma, slendro diesis
7 50/49 [1 0 2 -2⟩ 34.98 Biruyo Jubilisma, tritonic diesis
7 3136/3125 [6 0 -5 2⟩ 6.08 Zozoquingu Hemimean comma
7 6144/6125 [11 1 -3 -2⟩ 5.36 Sarurutrigu Porwell comma
7 2401/2400 [-5 -1 -2 4⟩ 0.72 Bizozogu Breedsma
11 121/120 [-3 -1 -1 0 2⟩ 14.37 Lologu Biyatisma
11 176/175 [4 0 -2 -1 1⟩ 9.86 Lorugugu Valinorsma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
13 13/12 [-2 -1 0 0 0 1⟩ 138.57 tho 2nd Tridecimal neutral second

Instruments

Any instruments that can play the full gamut of 12edo (ie, not diatonic harmonicas, dulcimers or harps) can obviously also play 6edo as well, although it is significantly more ergonomic on some instruments than others.

If you want a more specialist design making 6edo music easy to play without having to worry about hitting out of key 12edo notes, a Lumatone mapping for 6edo is available, or you could remove all the unwanted bars on a xylophone or marimba.

Music

Bryan Deister
Chimeratio
  • "Bowser breaks into Arnold Schoenberg's house and steals six of the twelve Tone Crystals (every other one), activating The 666666-Year-Curse Mechanism", from STAFFcirc vol. 7 (2021) – SoundCloud | Bandcamp
Milan Guštar
Aaron Andrew Hunt
NullPointerException Music
Phanomium
Chris Vaisvil
  • The Good Boundless (2011) – blog | play

Notes

  1. ↑ Based on treating 6edo as a subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup temperament; other approaches are also possible. For example, for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).
  2. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Retrieved from "https://en.xen.wiki/index.php?title=6edo&oldid=206396"