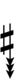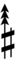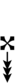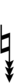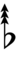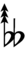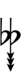89edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Cleanup
→Music: Add Bryan Deister's ''microtonal improvisation in 89edo'' (2025)
 
(16 intermediate revisions by 5 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|89}}
{{ED intro}}


== Theory ==
== Theory ==
89edo has a [[3/1|harmonic 3]] less than a cent flat and a [[5/1|harmonic 5]] less than five cents sharp, with a [[7/1|7]] two cents sharp and an [[11/1|11]] 1.5 cents sharp. It thus delivers reasonably good 11-limit harmony and very good no-fives harmony along with the very useful approximations represented by its commas. On a related note, a notable characteristic of this edo is that it is the lowest in a series of four consecutive edos to temper out [[quartisma]].
89edo has a [[3/1|harmonic 3]] less than a cent flat and a [[5/1|harmonic 5]] less than five cents sharp, with a [[7/1|7]] two cents sharp and an [[11/1|11]] 1.5 cents sharp. It thus delivers reasonably good 11-limit harmony and very good no-fives harmony along with the very useful approximations represented by its commas. On a related note, a notable characteristic of this edo is that it is the lowest in a series of four consecutive edos to temper out [[quartisma]].


89et [[tempering out|tempers out]] the commas 32805/32768 ([[schisma]]) in the 5-limit; [[126/125]], [[1728/1715]], and [[2401/2400]] in the 7-limit; and [[176/175]], [[243/242]], [[441/440]] and [[540/539]] in the 11-limit. It is an especially good tuning for the [[myna]] temperament, both in the [[7-limit]], tempering out 126/125 and 1728/1715, and in the [[11-limit]], where 176/175 is tempered out also. It is likewise a good tuning for the rank-3 temperament [[thrush]], tempering out 126/125 and 176/175.
It [[tempering out|tempers out]] 32805/32768 ([[schisma]]) in the 5-limit; [[126/125]], [[1728/1715]], and [[2401/2400]] in the 7-limit; and [[176/175]], [[243/242]], [[441/440]] and [[540/539]] in the 11-limit. It is an especially good tuning for the [[myna]] temperament, both in the [[7-limit]], tempering out 126/125 and 1728/1715, and in the [[11-limit]], where 176/175 is tempered out also. It is likewise a good tuning for the rank-3 temperament [[thrush]], tempering out 126/125 and 176/175.
 
The [[13-limit]] is a little tricky as [[13/1|13]] is tuned distinctly flat, tempering out [[169/168]], [[364/363]], [[729/728]], [[832/825]], and [[1287/1280]]. [[13/10]] and [[15/13]] are particularly out of tune in this system, each being about 9 cents off. The alternative 89f val fixes that but tunes [[13/8]] much sharper, conflating it with [[18/11]]. It tempers out [[144/143]], [[196/195]], [[351/350]], and [[352/351]] instead, and [[support]]s 13-limit myna and thrush. However, [[58edo]] is a better tuning for those purposes.
 
The [[17/1|17]] and [[19/1|19]] are tuned fairly well, making it [[consistent]] to the no-13 [[21-odd-limit]]. The equal temperament tempers out [[256/255]] and [[561/560]] in the 17-limit; and [[171/170]], [[361/360]], [[513/512]], and [[1216/1215]] in the 19-limit.
 
89edo is the 11th in the {{w|Fibonacci sequence}}, which means its 55th step approximates logarithmic φ (i.e. 1200{{nowrap|(φ − 1)}}{{c}} within a fraction of a cent.


=== Prime harmonics ===
=== Prime harmonics ===
Line 11: Line 17:


=== Subsets and supersets ===
=== Subsets and supersets ===
89edo is the 24th [[prime edo]], and the 11th in the Fibonacci sequence, which means its 55th step approximates logarithmic φ (i.e. (φ - 1)×1200 cents) within a fraction of a cent.
89edo is the 24th [[prime edo]], following [[83edo]] and before [[97edo]].


== Interval table ==
== Intervals ==
{{Interval table}}
{{Interval table}}
== Notation ==
=== Ups and downs notation ===
89edo can be notated using [[ups and downs notation]] using [[Helmholtz–Ellis]] accidentals:
{{Sharpness-sharp8}}
== Approximation to JI ==
=== Zeta peak index ===
{{ZPI
| zpi = 497
| steps = 89.0229355804124
| step size = 13.4796723133902
| tempered height = 7.567368
| pure height = 7.158697
| integral = 1.124501
| gap = 16.042570
| octave = 1199.69083589172
| consistent = 12
| distinct = 12
}}


== Regular temperament properties ==
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list|Comma List]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve Stretch (¢)
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning Error
! colspan="2" | Tuning error
|-
|-
! [[TE error|Absolute]] (¢)
! [[TE error|Absolute]] (¢)
Line 37: Line 65:
| 32805/32768, 10077696/9765625
| 32805/32768, 10077696/9765625
| {{mapping| 89 141 207 }}
| {{mapping| 89 141 207 }}
| -0.500
| −0.500
| 1.098
| 1.098
| 8.15
| 8.15
Line 44: Line 72:
| 126/125, 1728/1715, 32805/32768
| 126/125, 1728/1715, 32805/32768
| {{mapping| 89 141 207 250 }}
| {{mapping| 89 141 207 250 }}
| -0.550
| −0.550
| 0.955
| 0.955
| 7.08
| 7.08
Line 51: Line 79:
| 126/125, 176/175, 243/242, 16384/16335
| 126/125, 176/175, 243/242, 16384/16335
| {{mapping| 89 141 207 250 308 }}
| {{mapping| 89 141 207 250 308 }}
| -0.526
| −0.526
| 0.855
| 0.855
| 6.35
| 6.35
Line 58: Line 86:
=== Rank-2 temperaments ===
=== Rank-2 temperaments ===
{| class="wikitable center-all left-5"
{| class="wikitable center-all left-5"
|+ Table of rank-2 temperaments by generator
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator
|-
|-
! Periods<br>per 8ve
! Periods<br />per 8ve
! Generator*
! Generator*
! Cents*
! Cents*
! Associated<br>Ratio*
! Associated<br />ratio*
! Temperament
! Temperaments
|-
|-
| 1
| 1
Line 70: Line 98:
| 175.28
| 175.28
| 72/65
| 72/65
| [[Sesquiquartififths]] / [[Sesquart]]
| [[Sesquiquartififths]] / [[sesquart]]
|-
|-
| 1
| 1
Line 96: Line 124:
| [[Grackle]]
| [[Grackle]]
|}
|}
<nowiki>*</nowiki> [[Normal lists|octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if it is distinct
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct


== Scales ==
== Scales ==
Line 102: Line 130:
* [[Myna11]]
* [[Myna11]]
* [[Myna15]]
* [[Myna15]]
== Instruments ==
; Lumatone
''See [[Lumatone mapping for 89edo]].''


== Music ==
== Music ==
; [[Bryan Deister]]
* [https://www.youtube.com/watch?v=2JNIeqvXKlM ''microtonal improvisation in 89edo''] (2025)
; [[Francium]]
; [[Francium]]
* [https://www.youtube.com/watch?v=5Du9RfDUqCs ''Singing Golden Myna''] (2022) – myna[11] in 89edo
* [https://www.youtube.com/watch?v=5Du9RfDUqCs ''Singing Golden Myna''] (2022) – myna[11] in 89edo


[[Category:Listen]]
[[Category:Myna]]
[[Category:Myna]]
[[Category:Thrush]]
[[Category:Thrush]]
[[Category:Listen]]

Latest revision as of 17:30, 31 July 2025

← 88edo 89edo 90edo →
Prime factorization 89 (prime)
Step size 13.4831 ¢ 
Fifth 52\89 (701.124 ¢)
Semitones (A1:m2) 8:7 (107.9 ¢ : 94.38 ¢)
Consistency limit 11
Distinct consistency limit 11

89 equal divisions of the octave (abbreviated 89edo or 89ed2), also called 89-tone equal temperament (89tet) or 89 equal temperament (89et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 89 equal parts of about 13.5 ¢ each. Each step represents a frequency ratio of 21/89, or the 89th root of 2.

Theory

89edo has a harmonic 3 less than a cent flat and a harmonic 5 less than five cents sharp, with a 7 two cents sharp and an 11 1.5 cents sharp. It thus delivers reasonably good 11-limit harmony and very good no-fives harmony along with the very useful approximations represented by its commas. On a related note, a notable characteristic of this edo is that it is the lowest in a series of four consecutive edos to temper out quartisma.

It tempers out 32805/32768 (schisma) in the 5-limit; 126/125, 1728/1715, and 2401/2400 in the 7-limit; and 176/175, 243/242, 441/440 and 540/539 in the 11-limit. It is an especially good tuning for the myna temperament, both in the 7-limit, tempering out 126/125 and 1728/1715, and in the 11-limit, where 176/175 is tempered out also. It is likewise a good tuning for the rank-3 temperament thrush, tempering out 126/125 and 176/175.

The 13-limit is a little tricky as 13 is tuned distinctly flat, tempering out 169/168, 364/363, 729/728, 832/825, and 1287/1280. 13/10 and 15/13 are particularly out of tune in this system, each being about 9 cents off. The alternative 89f val fixes that but tunes 13/8 much sharper, conflating it with 18/11. It tempers out 144/143, 196/195, 351/350, and 352/351 instead, and supports 13-limit myna and thrush. However, 58edo is a better tuning for those purposes.

The 17 and 19 are tuned fairly well, making it consistent to the no-13 21-odd-limit. The equal temperament tempers out 256/255 and 561/560 in the 17-limit; and 171/170, 361/360, 513/512, and 1216/1215 in the 19-limit.

89edo is the 11th in the Fibonacci sequence, which means its 55th step approximates logarithmic φ (i.e. 1200(φ − 1) ¢ within a fraction of a cent.

Prime harmonics

Approximation of prime harmonics in 89edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.00 -0.83 +4.70 +1.96 +1.49 -4.57 +2.91 -0.88 +5.43 -4.86 +1.03
Relative (%) +0.0 -6.2 +34.8 +14.5 +11.1 -33.9 +21.6 -6.6 +40.3 -36.0 +7.7
Steps
(reduced) 		89
(0) 		141
(52) 		207
(29) 		250
(72) 		308
(41) 		329
(62) 		364
(8) 		378
(22) 		403
(47) 		432
(76) 		441
(85)

Subsets and supersets

89edo is the 24th prime edo, following 83edo and before 97edo.

Intervals

Steps Cents Approximate ratios Ups and downs notation
0 0 1/1 D
1 13.5 ^D, ^^E♭♭
2 27 ^^D, ^3E♭♭
3 40.4 41/40, 42/41 ^3D, v4E♭
4 53.9 31/30, 32/31, 33/32, 34/33 ^4D, v3E♭
5 67.4 27/26 v3D♯, vvE♭
6 80.9 22/21 vvD♯, vE♭
7 94.4 19/18, 37/35 vD♯, E♭
8 107.9 33/31 D♯, ^E♭
9 121.3 15/14, 29/27 ^D♯, ^^E♭
10 134.8 40/37 ^^D♯, ^3E♭
11 148.3 12/11, 37/34 ^3D♯, v4E
12 161.8 34/31 ^4D♯, v3E
13 175.3 21/19, 31/28, 41/37 v3D𝄪, vvE
14 188.8 29/26 vvD𝄪, vE
15 202.2 9/8 E
16 215.7 17/15 ^E, ^^F♭
17 229.2 8/7 ^^E, ^3F♭
18 242.7 23/20, 38/33 ^3E, v4F
19 256.2 22/19, 36/31 ^4E, v3F
20 269.7 7/6 v3E♯, vvF
21 283.1 20/17, 33/28 vvE♯, vF
22 296.6 19/16, 32/27 F
23 310.1 ^F, ^^G♭♭
24 323.6 41/34 ^^F, ^3G♭♭
25 337.1 17/14 ^3F, v4G♭
26 350.6 38/31 ^4F, v3G♭
27 364 21/17, 37/30 v3F♯, vvG♭
28 377.5 41/33 vvF♯, vG♭
29 391 vF♯, G♭
30 404.5 24/19 F♯, ^G♭
31 418 14/11 ^F♯, ^^G♭
32 431.5 41/32 ^^F♯, ^3G♭
33 444.9 22/17, 31/24 ^3F♯, v4G
34 458.4 30/23 ^4F♯, v3G
35 471.9 21/16 v3F𝄪, vvG
36 485.4 41/31 vvF𝄪, vG
37 498.9 4/3 G
38 512.4 39/29 ^G, ^^A♭♭
39 525.8 23/17, 42/31 ^^G, ^3A♭♭
40 539.3 15/11, 41/30 ^3G, v4A♭
41 552.8 11/8 ^4G, v3A♭
42 566.3 v3G♯, vvA♭
43 579.8 7/5 vvG♯, vA♭
44 593.3 31/22, 38/27 vG♯, A♭
45 606.7 27/19 G♯, ^A♭
46 620.2 10/7 ^G♯, ^^A♭
47 633.7 ^^G♯, ^3A♭
48 647.2 16/11 ^3G♯, v4A
49 660.7 22/15, 41/28 ^4G♯, v3A
50 674.2 31/21, 34/23 v3G𝄪, vvA
51 687.6 vvG𝄪, vA
52 701.1 3/2 A
53 714.6 ^A, ^^B♭♭
54 728.1 32/21, 35/23 ^^A, ^3B♭♭
55 741.6 23/15 ^3A, v4B♭
56 755.1 17/11 ^4A, v3B♭
57 768.5 v3A♯, vvB♭
58 782 11/7 vvA♯, vB♭
59 795.5 19/12 vA♯, B♭
60 809 A♯, ^B♭
61 822.5 37/23 ^A♯, ^^B♭
62 836 34/21 ^^A♯, ^3B♭
63 849.4 31/19 ^3A♯, v4B
64 862.9 28/17 ^4A♯, v3B
65 876.4 v3A𝄪, vvB
66 889.9 vvA𝄪, vB
67 903.4 27/16, 32/19 B
68 916.9 17/10 ^B, ^^C♭
69 930.3 12/7 ^^B, ^3C♭
70 943.8 19/11, 31/18 ^3B, v4C
71 957.3 33/19, 40/23 ^4B, v3C
72 970.8 7/4 v3B♯, vvC
73 984.3 30/17 vvB♯, vC
74 997.8 16/9 C
75 1011.2 ^C, ^^D♭♭
76 1024.7 38/21 ^^C, ^3D♭♭
77 1038.2 31/17 ^3C, v4D♭
78 1051.7 11/6 ^4C, v3D♭
79 1065.2 37/20 v3C♯, vvD♭
80 1078.7 28/15, 41/22 vvC♯, vD♭
81 1092.1 vC♯, D♭
82 1105.6 36/19 C♯, ^D♭
83 1119.1 21/11 ^C♯, ^^D♭
84 1132.6 ^^C♯, ^3D♭
85 1146.1 31/16, 33/17 ^3C♯, v4D
86 1159.6 41/21 ^4C♯, v3D
87 1173 v3C𝄪, vvD
88 1186.5 vvC𝄪, vD
89 1200 2/1 D

Notation

Ups and downs notation

89edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Sharp symbol  
Flat symbol

Approximation to JI

Zeta peak index

Tuning Strength Octave (cents) Integer limit
ZPI Steps
per 8ve 		Step size
(cents) 		Height Integral Gap Size Stretch Consistent Distinct
Tempered Pure
497zpi 89.022936 13.479672 7.567368 7.158697 1.124501 16.04257 1199.690836 −0.309164 12 12

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-141 89⟩ [⟨89 141]] +0.262 0.262 1.95
2.3.5 32805/32768, 10077696/9765625 [⟨89 141 207]] −0.500 1.098 8.15
2.3.5.7 126/125, 1728/1715, 32805/32768 [⟨89 141 207 250]] −0.550 0.955 7.08
2.3.5.7.11 126/125, 176/175, 243/242, 16384/16335 [⟨89 141 207 250 308]] −0.526 0.855 6.35

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperaments
1 13\89 175.28 72/65 Sesquiquartififths / sesquart
1 21\89 283.15 13/11 Neominor
1 23\89 310.11 6/5 Myna
1 29\89 391.01 5/4 Amigo
1 37\89 498.87 4/3 Grackle

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

Instruments

Lumatone

See Lumatone mapping for 89edo.

Music

Bryan Deister
Francium
Retrieved from "https://en.xen.wiki/index.php?title=89edo&oldid=205634"