Escapade family
- This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.
The escapade family of temperaments tempers out the escapade comma, [32 -7 -9⟩, of size 9.492 cents. The defining feature of this comma is splitting 5/3 into sixteen quartertones of which 5/4 makes up seven and 4/3 makes up nine; therefore 16/15 is two generator steps. It most naturally manifests as a 2.3.5.11-subgroup temperament, tempering out 4000/3993 and 5632/5625.
Extensions of escapade to incorporate prime 7 (and therefore the full 11-limit) include escapist (21 & 22), tempering out 225/224 and mapping 7 to −4 generators; escaped (22 & 87), tempering out 245/243 and mapping 7 to −26 generators; alphaquarter (65d & 87), tempering out 5120/5103 and mapping 7 to 61 generators; septisuperfourth (a.k.a. biscapade) (22 & 86), tempering out 6144/6125, splitting the octave in half and mapping 7 to −15 generators; and arch (43 & 87), tempering out 3136/3125 and splitting the generator into two 64/63 intervals; all are considered below.
Escapade
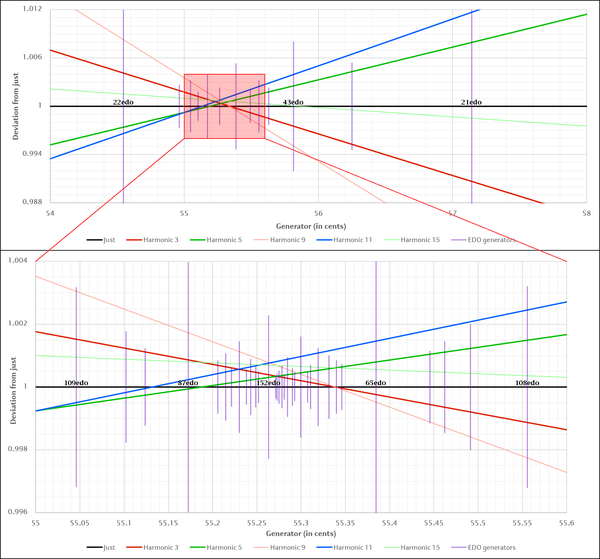
For intervals along the chain of generators in the 2.3.5.11.31 subgroup temperament, out to 22 generators up, see the third column of 16ed5/3#Intervals.
5-limit
Subgroup: 2.3.5
Comma list: 4294967296/4271484375 ([32 -7 -9⟩)
Mapping: [⟨1 2 2], ⟨0 -9 7]]
- mapping generators: ~2, ~16875/16384
Optimal ET sequence: 21, 22, 43, 65, 152, 217, 586, 803
Badness (Smith): 0.083778
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.253 | +0.298 |
| 5/4 | 387.136 | +0.823 |
2.3.5.11 subgroup
Since (an ideally slightly flat) 4/3 is split in three by the interval of 3 generators, it makes sense to equate that interval to 11/10 by tempering out 4000/3993, and therefore the generator to (11/10)/(16/15) = 33/32; this does minimal damage to the temperament. This structure in 2.3.5.11 occurs in all extensions of escapade to include prime 7, and therefore will be considered the fount of all further extensions.
Subgroup: 2.3.5.11
Comma list: 4000/3993 ([5 -1 3 -3⟩), 5632/5625 ([9 -2 -4 1⟩)
Mapping: [⟨1 2 2 3], ⟨0 -9 7 10]]
Optimal tuning (CTE): ~2 = 1200.0000, ~33/32 = 55.2760
Optimal ET sequence: 21, 22, 43, 65, 87, 152, 369, 521e, 1194bcee, 1715bceeee
Badness: 0.0107
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.516 | +0.561 |
| 5/4 | 386.932 | +0.618 |
| 11/8 | 552.760 | +1.442 |
2.3.5.11.31 subgroup
One may note that the generator represents the square root of 16/15 and therefore it would be logical to also temper out S31 = 961/960 so that the generator is equated to 32/31 ~ 31/30 in addition to 33/32.
Subgroup: 2.3.5.11.31
Comma list: 496/495 ([4 -2 -1 -1 1⟩), 961/960 ([-6 -1 -1 0 2⟩), 4000/3993 ([5 -1 3 -3 0⟩)
Mapping: [⟨1 2 2 3 5], ⟨0 -9 7 10 -1]]
Optimal tuning (CTE): ~2 = 1200.000, ~32/31 = 55.276
Optimal ET sequence: 21, 22, 43, 65, 87, 152, 369, 521e, 673e, 1194bcee, 1867bceeee
Badness (Sintel): 0.251
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.518 | +0.563 |
| 5/4 | 386.931 | +0.617 |
| 11/8 | 552.758 | +1.440 |
| 31/16 | 1144.724 | -0.311 |
Strong extensions
| Extension | Mapping of 7 | Tuning range* |
|---|---|---|
| Escapist | -4 | ↓ 65 |
| Alphaquarter | +61 | ↑ 65 ↓ 87 |
| Escaped | -26 | ↑ 87 |
* Defined as the range in which the extension specified has a better mapping of 7 compared to its neighboring extensions
Escaped
This temperament was also known as "sensa" in earlier materials because it tempers out 245/243, 352/351, and 385/384 as a sensamagic temperament. Not to be confused with the 19e & 27 temperament (sensi extension).
Here, 245/243 is tempered out so that 9/7 is equated to the square root of 5/3 (at 8 generators) present in the temperament. This works best where 5/3 is slightly flat, therefore on the end of the spectrum approaching 22edo.
7-limit
Subgroup: 2.3.5.7
Comma list: 245/243, 65625/65536
Mapping: [⟨1 2 2 4], ⟨0 -9 7 -26]]
Optimal tuning (POTE): ~2 = 1200.000, ~28/27 = 55.122
Optimal ET sequence: 22, 65, 87, 196, 283
Badness (Smith): 0.088746
11-limit
Subgroup: 2.3.5.7.11
Comma list: 245/243, 385/384, 4000/3993
Mapping: [⟨1 2 2 4 3], ⟨0 -9 7 -26 10]]
Optimal tuning (POTE): ~2 = 1200.000, ~28/27 = 55.126
Optimal ET sequence: 22, 65, 87, 196, 283
Badness (Smith): 0.035844
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 703.831 | +1.876 |
| 5/4 | 385.909 | -0.405 |
| 7/4 | 966.624 | -2.202 |
| 11/8 | 551.299 | -0.019 |
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 245/243, 352/351, 385/384, 625/624
Mapping: [⟨1 2 2 4 3 2], ⟨0 -9 7 -26 10 37]]
Optimal tuning (POTE): ~2 = 1200.000, ~28/27 = 55.138
Optimal ET sequence: 22, 65, 87, 283
Badness (Smith): 0.031366
Alphaquarter
Given the slightly sharp ~3/2 in ideal tunings of escapade (between 65edo and 87edo), it does very little damage to temper out 5120/5103 to extend it to prime 7; the cost is that the harmonic 7 is exceedingly complex, located all the way at 61 generators up.
7-limit
Subgroup: 2.3.5.7
Comma list: 5120/5103, 29360128/29296875
Mapping: [⟨1 2 2 0], ⟨0 -9 7 61]]
Optimal tuning (POTE): ~2 = 1200.000, ~16128/15625 = 55.243
Optimal ET sequence: 65d, 87, 152, 239, 391
Badness (Smith): 0.116594
11-limit
Subgroup: 2.3.5.7.11
Comma list: 3025/3024, 4000/3993, 5120/5103
Mapping: [⟨1 2 2 0 3], ⟨0 -9 7 61 10]]
Optimal tuning (POTE): ~2 = 1200.000, ~33/32 = 55.243
Optimal ET sequence: 65d, 87, 152, 239, 391
Badness (Smith): 0.029638
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.918 | +0.963 |
| 5/4 | 386.620 | +0.306 |
| 7/4 | 969.113 | +0.287 |
| 11/8 | 552.314 | +0.996 |
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 352/351, 625/624, 847/845, 1575/1573
Mapping: [⟨1 2 2 0 3 2], ⟨0 -9 7 61 10 37]]
Optimal tuning (POTE): ~2 = 1200.000, ~33/32 = 55.236
Optimal ET sequence: 65d, 87, 152f, 239f
Badness (Smith): 0.025344
Escapist
This temperament makes the identification of the 4-generator interval, representing (16/15)2, with 8/7 by tempering out 225/224 (along with 12288/12005); however, this is somewhat inaccurate as the ~16/15 in escapade is slightly flat, while for a good marvel tuning it needs to be tempered sharpward to equate it with 15/14.
7-limit
Subgroup: 2.3.5.7
Comma list: 225/224, 12288/12005
Mapping: [⟨1 2 2 3], ⟨0 -9 7 -4]]
Optimal tuning (POTE): ~2 = 1200.000, ~49/48 = 55.327
Optimal ET sequence: 21, 22, 43, 65d
Badness (Smith): 0.077950
11-limit
Subgroup: 2.3.5.7.11
Comma list: 99/98, 176/175, 2560/2541
Mapping: [⟨1 2 2 3 3], ⟨0 -9 7 -4 10]]
Optimal tuning (POTE): ~2 = 1200.000, ~33/32 = 55.354
Optimal ET sequence: 21, 22, 43, 65d
Badness (Smith): 0.036700
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 701.626 | -0.329 |
| 5/4 | 387.624 | +1.310 |
| 7/4 | 978.501 | +9.675 |
| 11/8 | 553.749 | +2.431 |
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 78/77, 99/98, 176/175, 507/500
Mapping: [⟨1 2 2 3 3 3], ⟨0 -9 7 -4 10 15]]
Optimal tuning (POTE): ~2 = 1200.000, ~26/25 = 55.550
Optimal ET sequence: 21, 22, 43
Badness (Smith): 0.035261
Weak extensions
| Extensions | Periods per octave | Position of original generator | |
|---|---|---|---|
| Number of generators | Number of periods | ||
| Septisuperfourth | period = 1/2 octave | 1 generator | + 0 periods |
| Arch | period = octave | 2 generators | + 0 periods |
Septisuperfourth
7-limit
Subgroup: 2.3.5.7
Comma list: 6144/6125, 118098/117649
Mapping: [⟨2 4 4 7], ⟨0 -9 7 -15]]
- mapping generators: ~343/243, ~16875/16384
Optimal tuning (POTE): ~343/243 = 1\2, ~16875/16384 = 55.320
Optimal ET sequence: 22, 86, 108, 130, 152, 282
Badness (Smith): 0.059241
11-limit
Subgroup: 2.3.5.7.11
Comma list: 540/539, 4000/3993, 5632/5625
Mapping: [⟨2 4 4 7 6], ⟨0 -9 7 -15 10]]
Optimal tuning (POTE): ~99/70 = 600.000, ~33/32 = 55.304
Optimal ET sequence: 22, 86, 108, 130, 152, 282
Badness (Smith): 0.024619
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.070 | +0.115 |
| 5/4 | 387.279 | +0.965 |
| 7/4 | 970.117 | +1.291 |
| 11/8 | 553.255 | +1.937 |
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 540/539, 729/728, 1575/1573, 3584/3575
Mapping: [⟨2 4 4 7 6 11], ⟨0 -9 7 -15 10 -39]]
Optimal tuning (POTE): ~99/70 = 600.000, ~33/32 = 55.325
Optimal ET sequence: 22f, 108f, 130, 282
Badness (Smith): 0.022887
Septisuperquad
This temperament is also known as "biscapade".
Subgroup: 2.3.5.7.11.13
Comma list: 351/350, 364/363, 540/539, 4096/4095
Mapping: [⟨2 4 4 7 6 5], ⟨0 -9 7 -15 10 26]]
Optimal tuning (POTE): ~55/39 = 600.000, ~33/32 = 55.359
Optimal ET sequence: 22, 108, 130
Badness (Smith): 0.033038
Arch
7-limit
Subgroup: 2.3.5.7
Comma list: 3136/3125, 5250987/5242880
Mapping: [⟨1 2 2 2], ⟨0 -18 14 35]]
- mapping generators: ~2, ~64/63
Optimal tuning (POTE): ~2 = 1\1, ~64/63 = 27.668
Optimal ET sequence: 43, 87, 130, 217, 347, 824c, 1171c, 1518cd
Badness (Smith): 0.094345
11-limit
Subgroup: 2.3.5.7.11
Comma list: 441/440, 3136/3125, 4000/3993
Mapping: [⟨1 2 2 2 3], ⟨0 -18 14 35 20]]
Optimal tuning (POTE): ~2 = 1200.000, ~64/63 = 27.663
Optimal ET sequence: 43, 87, 130, 217, 347e, 911cde
Badness (Smith): 0.036541
| Prime harmonic | Tunings | |
|---|---|---|
| CTE tuning | Deviation from just | |
| 3/2 | 702.178 | +0.223 |
| 5/4 | 387.195 | +0.881 |
| 7/4 | 967.987 | -0.839 |
| 11/8 | 553.135 | +1.817 |
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 364/363, 441/440, 676/675, 3136/3125
Mapping: [⟨1 2 2 2 3 4], ⟨0 -18 14 35 20 -13]]
Optimal tuning (POTE): ~2 = 1200.000, ~64/63 = 27.660
Optimal ET sequence: 43, 87, 130, 217, 347e, 564e
Badness (Smith): 0.019504