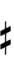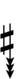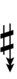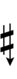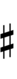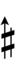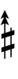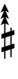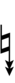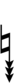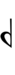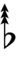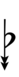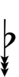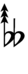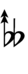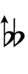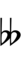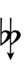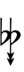75edo
| ← 74edo | 75edo | 76edo → |
75 equal divisions of the octave (abbreviated 75edo or 75ed2), also called 75-tone equal temperament (75tet) or 75 equal temperament (75et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 75 equal parts of exactly 16 ¢ each. Each step represents a frequency ratio of 21/75, or the 75th root of 2.
Theory
75et tempers out 20000/19683 (tetracot comma) and 2109375/2097152 (semicomma) in the 5-limit, and provides a good tuning for the tetracot temperament. It tempers out 225/224 and 1728/1715 in the 7-limit, supporting bunya and orwell, and providing the optimal patent val for fog.
In the 11-limit, 75e val ⟨75 119 174 211 260] (corresponding to 401zpi) scores lower in error, and tempers 100/99 and 243/242, whereas the patent val ⟨75 119 174 211 259] tempers 99/98 and 121/120. It tempers out 325/324 and 512/507 in the 13-limit, 120/119 and 256/255 in the 17-limit, and 190/189 and 250/247 in the 19-limit.
Since 75 is part of the Fibonacci sequence beginning with 5 and 12, it closely approximates the peppermint temperament. The size of its fifth is exactly 704 ¢, which is very close to the peppermint fifth of 704.096 cents. This makes it suitable for neo-Gothic tunings. It also approximates the Carlos Beta scale well (4\75 ≈ 1\Carlos Beta).
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +2.04 | -2.31 | +7.17 | +4.09 | -7.32 | +7.47 | -0.27 | +7.04 | +6.49 | -6.78 | -4.27 |
| Relative (%) | +12.8 | -14.5 | +44.8 | +25.6 | -45.7 | +46.7 | -1.7 | +44.0 | +40.5 | -42.4 | -26.7 | |
| Steps (reduced) |
119 (44) |
174 (24) |
211 (61) |
238 (13) |
259 (34) |
278 (53) |
293 (68) |
307 (7) |
319 (19) |
329 (29) |
339 (39) | |
Riemann zeta function
The Riemann zeta function includes two peaks of similar magnitude around 75edo: 400zpi and 401zpi, corresponding to the 75dfghk and 75eij vals, with differing mappings for all primes above 5. 400zpi tempers out 686/675, 875/864, and 5120/5103 in the 7-limit, 121/120 and 441/440 in the 11-limit, 91/90, 352/351, and 2080/2079 in the 13-limit, 136/135 in the 17-limit, 190/189 in the 19-limit, and 161/160 in the 23-limit. 401zpi tempers out 20000/19683, 1728/1715, and 225/224 in the 7-limit, 100/99 and 2200/2187 in the 11-limit, 144/143 and 275/273 in the 13-limit, 120/119 and 1225/1224 in the 17-limit, 190/189 in the 19-limit, and 162/161 in the 23-limit. Its step is mapped to 49/48 (the slendro diesis) in 400zpi, but 64/63 (Archytas' comma) in 401zpi and 75p.
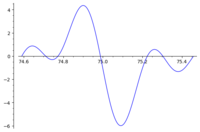
Compare how prime harmonics are mapped in each zeta peak:
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.59 | +4.57 | +1.37 | -4.37 | -1.83 | -2.66 | -2.47 | -2.77 | +2.91 | +2.14 | -1.17 |
| Relative (%) | +9.9 | +28.5 | +8.6 | -27.3 | -11.4 | -16.6 | -15.4 | -17.3 | +18.2 | +13.4 | -7.3 | |
| Step | 75 | 119 | 174 | 210 | 259 | 277 | 306 | 318 | 339 | 364 | 371 | |
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -1.46 | -0.27 | -5.69 | +3.08 | +3.63 | +2.07 | +1.08 | +0.29 | +5.12 | +3.34 | -0.26 |
| Relative (%) | -9.1 | -1.7 | -35.6 | +19.3 | +22.7 | +13.0 | +6.8 | +1.8 | +32.1 | +20.9 | -1.6 | |
| Step | 75 | 119 | 174 | 211 | 260 | 278 | 307 | 319 | 340 | 365 | 372 | |
Intervals
| Steps | Cents | Approximate ratios | Ups and downs notation |
|---|---|---|---|
| 0 | 0 | 1/1 | D |
| 1 | 16 | ^D, v4E♭ | |
| 2 | 32 | ^^D, v3E♭ | |
| 3 | 48 | 35/34, 36/35, 37/36, 38/37 | ^3D, vvE♭ |
| 4 | 64 | 27/26, 28/27 | ^4D, vE♭ |
| 5 | 80 | 23/22 | v3D♯, E♭ |
| 6 | 96 | 18/17, 19/18, 37/35 | vvD♯, ^E♭ |
| 7 | 112 | 16/15 | vD♯, ^^E♭ |
| 8 | 128 | 14/13 | D♯, ^3E♭ |
| 9 | 144 | 25/23, 37/34, 38/35 | ^D♯, v4E |
| 10 | 160 | 34/31 | ^^D♯, v3E |
| 11 | 176 | 21/19, 31/28 | ^3D♯, vvE |
| 12 | 192 | 19/17 | ^4D♯, vE |
| 13 | 208 | 35/31 | E |
| 14 | 224 | 25/22, 33/29 | ^E, v4F |
| 15 | 240 | 23/20, 31/27 | ^^E, v3F |
| 16 | 256 | 29/25, 36/31 | ^3E, vvF |
| 17 | 272 | ^4E, vF | |
| 18 | 288 | F | |
| 19 | 304 | 31/26, 37/31 | ^F, v4G♭ |
| 20 | 320 | ^^F, v3G♭ | |
| 21 | 336 | 17/14 | ^3F, vvG♭ |
| 22 | 352 | 38/31 | ^4F, vG♭ |
| 23 | 368 | 21/17, 26/21 | v3F♯, G♭ |
| 24 | 384 | 5/4 | vvF♯, ^G♭ |
| 25 | 400 | 29/23, 34/27 | vF♯, ^^G♭ |
| 26 | 416 | F♯, ^3G♭ | |
| 27 | 432 | 9/7 | ^F♯, v4G |
| 28 | 448 | 35/27 | ^^F♯, v3G |
| 29 | 464 | 17/13 | ^3F♯, vvG |
| 30 | 480 | 29/22, 33/25, 37/28 | ^4F♯, vG |
| 31 | 496 | 4/3 | G |
| 32 | 512 | 35/26 | ^G, v4A♭ |
| 33 | 528 | 19/14 | ^^G, v3A♭ |
| 34 | 544 | 26/19, 37/27 | ^3G, vvA♭ |
| 35 | 560 | 18/13 | ^4G, vA♭ |
| 36 | 576 | v3G♯, A♭ | |
| 37 | 592 | 38/27 | vvG♯, ^A♭ |
| 38 | 608 | 27/19, 37/26 | vG♯, ^^A♭ |
| 39 | 624 | 33/23 | G♯, ^3A♭ |
| 40 | 640 | 13/9, 29/20 | ^G♯, v4A |
| 41 | 656 | 19/13, 35/24 | ^^G♯, v3A |
| 42 | 672 | 28/19, 31/21 | ^3G♯, vvA |
| 43 | 688 | ^4G♯, vA | |
| 44 | 704 | 3/2 | A |
| 45 | 720 | ^A, v4B♭ | |
| 46 | 736 | 26/17 | ^^A, v3B♭ |
| 47 | 752 | 37/24 | ^3A, vvB♭ |
| 48 | 768 | 14/9 | ^4A, vB♭ |
| 49 | 784 | v3A♯, B♭ | |
| 50 | 800 | 27/17 | vvA♯, ^B♭ |
| 51 | 816 | 8/5 | vA♯, ^^B♭ |
| 52 | 832 | 21/13, 34/21 | A♯, ^3B♭ |
| 53 | 848 | 31/19 | ^A♯, v4B |
| 54 | 864 | 28/17, 33/20 | ^^A♯, v3B |
| 55 | 880 | ^3A♯, vvB | |
| 56 | 896 | ^4A♯, vB | |
| 57 | 912 | B | |
| 58 | 928 | ^B, v4C | |
| 59 | 944 | 31/18 | ^^B, v3C |
| 60 | 960 | ^3B, vvC | |
| 61 | 976 | ^4B, vC | |
| 62 | 992 | C | |
| 63 | 1008 | 34/19 | ^C, v4D♭ |
| 64 | 1024 | 38/21 | ^^C, v3D♭ |
| 65 | 1040 | 31/17 | ^3C, vvD♭ |
| 66 | 1056 | 35/19 | ^4C, vD♭ |
| 67 | 1072 | 13/7 | v3C♯, D♭ |
| 68 | 1088 | 15/8 | vvC♯, ^D♭ |
| 69 | 1104 | 17/9, 36/19 | vC♯, ^^D♭ |
| 70 | 1120 | C♯, ^3D♭ | |
| 71 | 1136 | 27/14 | ^C♯, v4D |
| 72 | 1152 | 35/18, 37/19 | ^^C♯, v3D |
| 73 | 1168 | ^3C♯, vvD | |
| 74 | 1184 | ^4C♯, vD | |
| 75 | 1200 | 2/1 | D |
Notation
Sagittal notation
This notation uses the same sagittal sequence as 68-EDO.
Evo flavor

Revo flavor

Evo-SZ flavor

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
Ups and downs notation
75edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||||||||||||
| Flat symbol |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [119 -75⟩ | [⟨75 119]] | −0.645 | 0.645 | 4.03 |
| 2.3.5 | 20000/19683, 2109375/2097152 | [⟨75 119 174]] | −0.099 | 0.936 | 5.85 |
| 2.3.5.7 | 225/224, 1728/1715, 15625/15309 | [⟨75 119 174 211]] | −0.713 | 1.337 | 8.36 |
Instruments
A Lumatone mapping for 75edo is available.
Music
- microtonal improvisation in 75edo (2025-06-22)
- microtonal improvisation in 75edo (2025-06-24)
- Waltz in 75edo (2025) short clip demonstrating diatonic Lumatone mapping
- Fugue on The Lick (2019)