11edo

← 10edo

11edo

12edo →

Prime factorization

11 (prime)

Step size

109.091¢

Fifth

6\11 (654.545¢)

Semitones (A1:m2)

-2:3 (-218.2¢ : 327.3¢)

Dual sharp fifth

7\11 (763.636¢)

Dual flat fifth

6\11 (654.545¢)

Dual major 2nd

2\11 (218.182¢)
(semiconvergent)

Consistency limit

3

Distinct consistency limit

3

11 equal divisions of the octave (abbreviated 11edo or 11ed2), also called 11-tone equal temperament (11tet) or 11 equal temperament (11et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 11 equal parts of about 109 ¢ each. Each step represents a frequency ratio of 2^1/11, or the 11th root of 2.

Theory

Approximation of odd harmonics in 11edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-47.4	+50.0	+13.0	+14.3	-5.9	+32.2	+2.6	+4.1	+29.8	-34.4	+26.3
Error	Relative (%)	-43.5	+45.9	+11.9	+13.1	-5.4	+29.5	+2.4	+3.8	+27.3	-31.5	+24.1
Steps (reduced)		17 (6)	26 (4)	31 (9)	35 (2)	38 (5)	41 (8)	43 (10)	45 (1)	47 (3)	48 (4)	50 (6)

Being less than twelve, 11edo maps easily to the standard keyboard. The suggested mapping disregards the Ab/G# key, leaving Orgone[7] on the whites. The superfluous Ab can be made a note of 22edo, a tuning known as "elevenplus".

Compared to 12edo, the intervals of 11edo are stretched:

The "minor second," at 109.09 cents, functions melodically very much like the 100-cent minor second of 12edo.
The "major second," at 218.18 cents, works in a similar fashion to the 200-cent major second of 12edo, but as a major ninth, it may sound less concordant. Its inversion, at 981.82 cents, can function as a "bluesy" seventh relative to 12edo's 1000-cent interval, although it is still about 13 cents away from 7/4.
The "minor third," at 327.27 cents, is rather sharp and encroaching upon "neutral third."
The "major third," at 436.36 cents, is quite sharp, and closer to the supermajor third of frequency ratio 9/7 than the simpler third of 5/4.
The "perfect fourth," at 545.45 cents, does not sound like a perfect fourth at all, and passes more easily as the 11/8 superfourth than the simpler perfect fourth of 4/3.

11edo provides the same tuning on the 2*11 subgroup 2.9.15.7.11.17 as does 22edo, and on this subgroup it tempers out the same commas as 22. Also on this subgroup there is an approximation of the 8:9:11:14:15:16:17 chord and its subchords. Though the error is rather large, this does provide 11 with a variety of chords approximating JI chords.

11edo is the largest edo that patently alternates with an undivided 9/8 in a wtn.

11edo has a good approximation of 9/7, hence one natural approach to harmony in 11edo is to generate chords from stacks of this interval. Incidentally, correcting the tuning of 9/7 to just tuning and stacking this interval has the beneficial side effect of also improving the tuning of the 17th harmonic to almost exactly just intonation, with an error of only 0.3 cents. It may therefore be worth considering this JI tuning as an alternative to 11edo.

A 0-8-16-20 chord in 11edo illustrating harmony generated from stacking 9/7 intervals.

Intervals and notation

11edo can be notated using ups and downs. Conventional notation, including the staff, note names, relative notation, etc. can be used in two ways. The first preserves the melodic meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5.

The second approach preserves the harmonic meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 11edo "on the fly".

The 11edo solfege in the table is derived from 22edo solfege.

#	Cents	Solfege	Approximate Ratios*	Sagittal notation (22edo subset)	Up/down notation with major wider than minor		Up/down notation with major narrower than minor		Smitonic (3rd-gen) notation	TDW Machine notation	Pseudo-Diatonic Category
0	0.00	do	1/1	A	P1	A	P1	A	A	Q, P#	Unison
1	109.09	ra	15/14, 16/15, 17/16, 18/17	AII\ or B!!/	^1, m2	^A, B	^1, M2	^A, B	A#, Bb	Q#, Rb	Minor second
2	218.18	re	8/7, 9/8, 17/15	B	~2, m3	^B, Cb	~2, M3	^B, C#	B	R	Major second
3	327.27	me	6/5, 11/9, 17/14	C/I or BII\ or D\!!/	M2, ~3	B#, vC	m2, ~3	Bb, vC	C	R#, Sb	Minor third
4	436.36	mo	9/7, 14/11, 22/17	D\! or C/II\	M3, v4	C, vD	m3, v4	C, vD	C#, Db	S	Major third/Minor fourth
5	545.45	fu	11/8, 15/11	D/I or E\!!/	P4, v5	D, vE	P4, v5	D, vE	D	S#, Tb	Major fourth
6	654.55	su	16/11, 22/15	E\! or D/II\	^4, P5	^D, E	^4, P5	^D, E	D#, Eb	T	Minor fifth
7	763.64	lo	14/9, 11/7, 17/11	F	^5, m6	^E, Fb	^5, M6	^E, F#	E	T#, Ub	Major fifth/Minor sixth
8	872.73	la	5/3, 18/11, 28/17	FII\ or G!!/	~6, m7	vF, Gb	~6, M7	vF, G#	F	U	Major sixth
9	981.82	ta	7/4, 16/9, 30/17	G	M6, ~7	F, vG	m6, ~7	F, vG	F#, Gb	U#, Pb	Minor seventh
10	1090.91	ti	15/8, 17/9, 28/15, 32/17	GII\ or A!!/	M7, v8	G, vAv	m7, v8	G, vAv	G	P, Qb	Major seventh
11	1200.00	do	2/1	A	P8	A	P8	A	A	Q, P#	Octave

in 2.7.9.11.15.17 subgroup

11edo in Sagittal notation:

Sagittal and up/down notations are heptatonic systems generated by 5ths (~3/2). Alternative notations include pentatonic 5th-generated, octatonic 5th-generated, nonatonic 5th-generated, heptatonic 3rd-generated, and hexatonic 2nd-generated.

Pentatonic 5th-generated: D * * E G * * A C * * D (Sensoid generator = wide 3/2 = 7\11 = perfect 5thoid)

D - ^D/Eb - D#/vE - E - G - ^G/Ab - G#/vA - A - C - ^C/Db - C#/vD - D

P1 - ^1/ms3 - A1/~s3 - Ms3 - P4d - ^4d/d5d - A4d/v5d - P5d - ms7 - ~s7/d8d - Ms7/v8d - P8d (s = sub-, d = -oid)

pentatonic genchain of fifths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...

pentatonic genchain of fifths: ...ds3 - ds7 - d4d - d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1 - A5d - As3 - As7... (s = sub-, d = -oid)

Octatonic 5th-generated: A B * C D E * F G * H A (Sensoid generator = wide 3/2 = 7\11 = perfect 6th)

A - B - B#/Cb - C - D - E - E#/Fb - F - G - G#/Hb - H - A

P1 - m2 - M2/m3 - M3 - P4 - m5 - M5 - P6 - m7 - M7/m8 - M8 - P9

octatonic genchain of sixths: ...Db - Ab - Fb - Cb - Hb - E - B - G - D - A - F - C - H - E# - B# - G# - D# - A#...

octatonic genchain of sixths: ...d7 - d4 - d9 - d6 - m3 - m8 - m5 - m2 - m7 - P4 - P1 - P6 - M3 - M8 - M5 - M2 - M7 - A4 - A1 - A6 - A3...

Nonatonic 5th-generated: A B * C D E F G * H J A (Joanatonic generator = narrow 3/2 = 6\11 = perfect 6th)

A - B - B#/Cb - C - D - E - F - G - G#/Hb - H - J - A

P1 - m2 - M2/m3 - M3/m4 - M4 - P5 - P6 - m7 - M7/m8 - M8/m9 - M9 - P10

nonotonic genchain of sixths: ...E# - A# - F# - B# - G# - C - H - D - J - E - A - F - B - G - Cb - Hb - Db - Jb - Eb...

nonotonic genchain of sixths: ...M2 - M7 - M3 - M8 - M4 - M9 - P5 - P1 - P6 - m2 - m7 - m3 - m8 - m4 - m9...

Heptatonic 3rd-generated: D * E F * G A * B C * D (Smitonic generator = 3\11 = perfect 3rd)

D - D#/Eb - E - F - F#/Gb - G - A - A#/Bb - B - C - C#/Db - D

P1 - m2 - M2 - P3 - m4 - M4 - m5 - M5 - P6 - m7 - M7 - P8

genchain of thirds: ...E# - G# - B# - D# - F# - A# - C# - E - G - B - D - F - A - C - Eb - Gb - Bb - Db - Fb - Ab - Cb...

genchain of thirds: ...M5 - M7 - M2 - M4 - P6 - P1 - P3 - m5 - m7 - m2 - m4 - d6...

Hexatonic 2nd-generated: R * S * T * U * P Q * R (Machinoid generator = 2\11 = perfect 2nd)

R - R#/Sb - S - S#/Tb - T - T#/Ub - U - U#/Pb - P - Q - Q#/Rb - R

P1 - A1/d2 - P2 - m3 - M3 - m4 - M4 - m5 - M5 - P6 - A6/d7 - P7

genchain of seconds: ... - Qb - Rb - Sb - Tb - Ub - Pb - Q - R - S - T - U - P - Q# - R# - S# - T# - U# - P#...

genchain of seconds: ... - m3 - m4 - m5 - P6 - P1 - P2 - M3 - M4 - M5 - A6 - A1...

Regular temperament properties

Uniform maps

13-limit uniform maps between 10.5 and 11.5
Min. size	Max. size	Wart notation	Map
10.5000	10.5081	11cccdddeeeefff	⟨11 17 24 29 36 39]
10.5081	10.5509	11cccdeeeefff	⟨11 17 24 30 36 39]
10.5509	10.5516	11cccdeefff	⟨11 17 24 30 37 39]
10.5516	10.6744	11cdeefff	⟨11 17 25 30 37 39]
10.6744	10.8399	11cdeef	⟨11 17 25 30 37 40]
10.8399	10.8643	11cdf	⟨11 17 25 30 38 40]
10.8643	10.9446	11cf	⟨11 17 25 31 38 40]
10.9446	10.9823	11c	⟨11 17 25 31 38 41]
10.9823	11.0413	11	⟨11 17 26 31 38 41]
11.0413	11.1290	11b	⟨11 18 26 31 38 41]
11.1290	11.2149	11be	⟨11 18 26 31 39 41]
11.2149	11.2205	11beff	⟨11 18 26 31 39 42]
11.2205	11.4129	11bddeff	⟨11 18 26 32 39 42]
11.4129	11.4181	11bccddeff	⟨11 18 27 32 39 42]
11.4181	11.4851	11bccddeeeff	⟨11 18 27 32 40 42]
11.4851	11.5000	11bccddeeeffff	⟨11 18 27 32 40 43]

Commas

11edo tempers out the following commas. (Note: This assumes val ⟨11 17 26 31 38 41].)

Prime limit	Ratio^{[note 1]}	Monzo	Cents	Color name	Name(s)
3	177147/131072	[-17 11⟩	521.50	sasawa 3rd	Pythagorean augmented third
5	135/128	[-7 3 1⟩	92.18	Layobi	Major chroma
5	(16 digits)	[-25 7 6⟩	31.57	Lala-tribiyo	Ampersand's comma
5	(42 digits)	[-68 18 17⟩	2.52	Quinla-seyo	Vavoom
7	(18 digits)	[-10 7 8 -7⟩	22.41	Lasepru-aquadbiyo	Blackjackisma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Marvel comma
7	16875/16807	[0 3 4 -5⟩	6.99	Quinru-aquadyo	Mirkwai
7	2401/2400	[-5 -1 -2 4⟩	0.72	Bizozogu	Breedsma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
11	65536/65219	[16 0 0 -2 -3⟩	8.39	Satrilu-aruru	Orgonisma

Approximation to JI

Harmonic	8		9		11		14		16
JI interval from 1/1	1/1 = 0 cents		9/8 = 204		11/8 = 551		7/4 = 969		2/1 = 1200
Nearest 11edo interval	0\11 = 0¢		2\11 = 218¢		5\11 = 545		9\11 = 982		11\11 = 1200
Difference	0		+14¢		-6¢		+13¢		0¢
JI interval between		9:8 = 204¢		11:9 = 347		14:11 = 418		8:7 = 231
Nearest 11edo interval		2\11 = 218¢		3\11 = 327		4\11 = 436		2\11 = 218
Difference		+14¢		-20¢		+18¢		-13¢

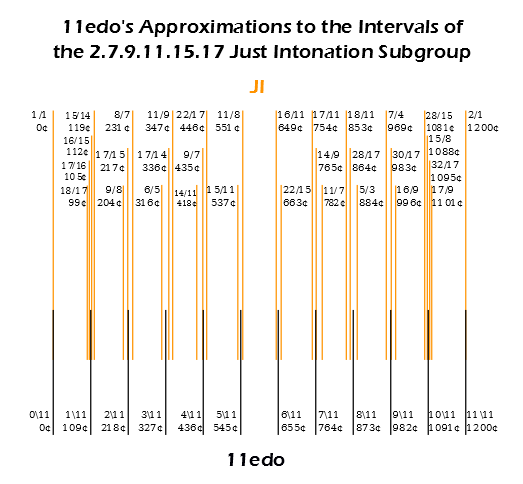
11edo also may be considered a 2.7.9.11.15.17 subgroup temperament. See diagram:

Scales

Main article: 11edo modes

MOS scales

Main article: List of 11edo MOS scales

Although 11edo has one fewer interval in the octave than 12edo, in terms of moment-of-symmetry scales, it offers a great deal more variety. This is because 11 is a prime number, while 12 is composite. Cycles of 2\11 (two degrees of 11edo), 3\11, 4\11 and 5\11 produce scales which do not repeat at the octave until all 11 intervals have been included.

Pathological modes

2 1 1 1 2 1 1 1 1 2L 7s MOS

3 1 1 1 1 1 1 1 1 1L 8s MOS

2 1 1 1 1 1 1 1 1 1 1L 9s MOS

Instruments

11edo ukulele

Ensembles

In February 2011, Oddmusic U-C, as part of its Microtonal Design Seminar, generated a 7-piece ensemble for playing music in 11edo. Instrumentation: autotuner, cümbüş, electronic keyboard, kalimba, retrofretted guitar, tuned bottles, udderbot. Recordings forthcoming.

Lumatone

There is a Lumatone mapping for 11edo.

Introductory Materials

11edo example composition by Inthar (first half's in 4L 3s, second half is in 3L 5s)

Music

See also: Category:11edo tracks

Strict 11edo

Modern renderings

Arthur Schutt

Bluin' The Black Keys (1926) – rendered by Francium (2024)

20th century

George Secor

First Piece Ever⁠ ⁠^[dead link] (1970) — apparently the first piece ever written for 11edo.

Bill Sethares

"The Turquoise Dabo Girl", from Xentonality (1997)

21st century

Abnormality

Scatter Brain (2024)

Christopher Bailey

The Stuffed Ones (2004) – 4-piece suite (details)
- "Goopy" · "Ellie" · "Ziggy" · "Towelbear"

Jacob Barton

Hyperimprovisations Nuggetwarp (2009)
- "Piece I" · "Piece II" · "Piece III"

City of the Asleep

"She is My Lilac-Hued Obsession", from Map of an Internal Landscape (2007)

Jason Conklin

The City Sleeps, A Madrigal (2011) – play | SoundCloud

E8 Heterotic

Olive Flamenco (2019)

Francium

"Tostadosto" from The Decatonic Album (2024) – Spotify | Bandcamp | YouTube
Sleep Slope (2024)

David Hamill

Cool My Head (2010)

Andrew Heathwaite

Orange Clips on Sausages (2004) – play | SoundClick
Blue Gel (2004) – play | SoundClick
conversation is (2010) – play | SoundClick

Hideya

Like Parker 3 (2019)
Like 40s music (2022)

Aaron Andrew Hunt

From The Equal-Tempered Keyboard (1999–2022)
- "Prelude in 11ET"
- "Adagio in 11ET" – Bandcamp | SoundCloud⁠ ⁠^[dead link]
- "Invention in 11ET" – Bandcamp | SoundCloud⁠ ⁠^[dead link]

Alexandru Ianu

Divertimento in 11 tone Orgone (2021) – sheet music | YouTube – orgone in 11edo tuning
Sylvian Moon Dance (2021) – audio | sheet music | YouTube – orgone in 11edo tuning
Ocean of the Necrophages (2021) – orgone in 11edo tuning
- Piano: audio | sheet music | YouTube
- Strings: audio | sheet music