53edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Move temperament measures to RTT properties section
Move temperament generator info to RTT section
Line 91: Line 91:
! Cents
! Cents
! Approximate ratios*
! Approximate ratios*
! colspan="3" | [[Ups_and_Downs_Notation|Ups and downs notation]]
! colspan="3" | [[Ups and downs notation]]
! Generator for
|-
|-
| 0
| 0
Line 101: Line 100:
| unison
| unison
| D
| D
|
|-
|-
| 1
| 1
Line 110: Line 108:
| up unison
| up unison
| ^D
| ^D
|
|-
|-
| 2
| 2
Line 119: Line 116:
| double-up unison, <br>double-down minor 2nd
| double-up unison, <br>double-down minor 2nd
| ^^D, <br>vvEb
| ^^D, <br>vvEb
| [[Quartonic]]
|-
|-
| 3
| 3
Line 128: Line 124:
| downminor 2nd
| downminor 2nd
| vEb
| vEb
|
|-
|-
| 4
| 4
Line 137: Line 132:
| minor 2nd
| minor 2nd
| Eb
| Eb
|
|-
|-
| 5
| 5
Line 146: Line 140:
| upminor 2nd
| upminor 2nd
| ^Eb
| ^Eb
|
|-
|-
| 6
| 6
Line 155: Line 148:
| downmid 2nd
| downmid 2nd
| ^^Eb
| ^^Eb
|
|-
|-
| 7
| 7
Line 164: Line 156:
| upmid 2nd
| upmid 2nd
| vvE
| vvE
| [[Hemikleismic]]
|-
|-
| 8
| 8
Line 173: Line 164:
| downmajor 2nd
| downmajor 2nd
| vE
| vE
|
|-
|-
| 9
| 9
Line 182: Line 172:
| major 2nd
| major 2nd
| E
| E
|
|-
|-
| 10
| 10
Line 191: Line 180:
| upmajor 2nd
| upmajor 2nd
| ^E
| ^E
|
|-
|-
| 11
| 11
Line 200: Line 188:
| double-up major 2nd, <br>double-down minor 3rd
| double-up major 2nd, <br>double-down minor 3rd
| ^^E, <br>vvF
| ^^E, <br>vvF
| [[Hemischis]]
|-
|-
| 12
| 12
Line 209: Line 196:
| downminor 3rd
| downminor 3rd
| vF
| vF
| [[Orwell]]
|-
|-
| 13
| 13
Line 218: Line 204:
| minor 3rd
| minor 3rd
| F
| F
|
|-
|-
| 14
| 14
Line 227: Line 212:
| upminor 3rd
| upminor 3rd
| ^F
| ^F
| [[Hanson]]/[[Catakleismic]]
|-
|-
| 15
| 15
Line 236: Line 220:
| downmid 3rd
| downmid 3rd
| ^^F
| ^^F
| [[Amity]]/[[Hitchcock]]
|-
|-
| 16
| 16
Line 245: Line 228:
| upmid 3rd
| upmid 3rd
| vvF#
| vvF#
|
|-
|-
| 17
| 17
Line 254: Line 236:
| downmajor 3rd
| downmajor 3rd
| vF#
| vF#
|
|-
|-
| 18
| 18
Line 263: Line 244:
| major 3rd
| major 3rd
| F#
| F#
|
|-
|-
| 19
| 19
Line 272: Line 252:
| upmajor 3rd
| upmajor 3rd
| ^F#
| ^F#
| [[Hamity]]
|-
|-
| 20
| 20
Line 281: Line 260:
| double-up major 3rd, <br>double-down 4th
| double-up major 3rd, <br>double-down 4th
| ^^F#, <br>vvG
| ^^F#, <br>vvG
|
|-
|-
| 21
| 21
Line 290: Line 268:
| down 4th
| down 4th
| vG
| vG
| [[Vulture]]/[[Buzzard]]
|-
|-
| 22
| 22
Line 299: Line 276:
| perfect 4th
| perfect 4th
| G
| G
|
|-
|-
| 23
| 23
Line 308: Line 284:
| up 4th
| up 4th
| ^G
| ^G
|
|-
|-
| 24
| 24
Line 317: Line 292:
| downmid 4th
| downmid 4th
| ^^G
| ^^G
|
|-
|-
| 25
| 25
Line 326: Line 300:
| upmid 4th, <br>downdim 5th
| upmid 4th, <br>downdim 5th
| vvG#, <br>vAb
| vvG#, <br>vAb
| [[Tricot]]
|-
|-
| 26
| 26
Line 335: Line 308:
| downaug 4th, <br>dim 5th
| downaug 4th, <br>dim 5th
| vG#, <br>Ab
| vG#, <br>Ab
|
|-
|-
| 27
| 27
Line 344: Line 316:
| aug 4th, <br>updim 5th
| aug 4th, <br>updim 5th
| G#, <br>^Ab
| G#, <br>^Ab
|
|-
|-
| 28
| 28
Line 353: Line 324:
| upaug 4th, <br>downmid 5th
| upaug 4th, <br>downmid 5th
| ^G#, <br>^^Ab
| ^G#, <br>^^Ab
|
|-
|-
| 29
| 29
Line 362: Line 332:
| upmid 5th
| upmid 5th
| vvA
| vvA
|
|-
|-
| 30
| 30
Line 371: Line 340:
| down 5th
| down 5th
| vA
| vA
|
|-
|-
| 31
| 31
Line 380: Line 348:
| perfect 5th
| perfect 5th
| A
| A
| [[Helmholtz]]/[[Garibaldi]]
|-
|-
| 32
| 32
Line 389: Line 356:
| up 5th
| up 5th
| ^A
| ^A
|
|-
|-
| 33
| 33
Line 398: Line 364:
| double-up 5th, <br>double-down minor 6th
| double-up 5th, <br>double-down minor 6th
| ^^A, <br>vvBb
| ^^A, <br>vvBb
|
|-
|-
| 34
| 34
Line 407: Line 372:
| downminor 6th
| downminor 6th
| vBb
| vBb
|
|-
|-
| 35
| 35
Line 416: Line 380:
| minor 6th
| minor 6th
| Bb
| Bb
|
|-
|-
| 36
| 36
Line 425: Line 388:
| upminor 6th
| upminor 6th
| ^Bb
| ^Bb
|
|-
|-
| 37
| 37
Line 434: Line 396:
| downmid 6th
| downmid 6th
| ^^Bb
| ^^Bb
|
|-
|-
| 38
| 38
Line 443: Line 404:
| upmid 6th
| upmid 6th
| vvB
| vvB
|
|-
|-
| 39
| 39
Line 452: Line 412:
| downmajor 6th
| downmajor 6th
| vB
| vB
|
|-
|-
| 40
| 40
Line 461: Line 420:
| major 6th
| major 6th
| B
| B
|
|-
|-
| 41
| 41
Line 470: Line 428:
| upmajor 6th
| upmajor 6th
| ^B
| ^B
|
|-
|-
| 42
| 42
Line 479: Line 436:
| double-up major 6th, <br>double-down minor 7th
| double-up major 6th, <br>double-down minor 7th
| ^^B, <br>vvC
| ^^B, <br>vvC
|
|-
|-
| 43
| 43
Line 488: Line 444:
| downminor 7th
| downminor 7th
| vC
| vC
|
|-
|-
| 44
| 44
Line 497: Line 452:
| minor 7th
| minor 7th
| C
| C
|
|-
|-
| 45
| 45
Line 506: Line 460:
| upminor 7th
| upminor 7th
| ^C
| ^C
|
|-
|-
| 46
| 46
Line 515: Line 468:
| downmid 7th
| downmid 7th
| ^^C
| ^^C
|
|-
|-
| 47
| 47
Line 524: Line 476:
| upmid 7th
| upmid 7th
| vvC#
| vvC#
|
|-
|-
| 48
| 48
Line 533: Line 484:
| downmajor 7th
| downmajor 7th
| vC#
| vC#
|
|-
|-
| 49
| 49
Line 542: Line 492:
| major 7th
| major 7th
| C#
| C#
|
|-
|-
| 50
| 50
Line 551: Line 500:
| upmajor 7th
| upmajor 7th
| ^C#
| ^C#
|
|-
|-
| 51
| 51
Line 560: Line 508:
| double-up major 7th, <br>double-down 8ve
| double-up major 7th, <br>double-down 8ve
| ^^C#, <br>vvD
| ^^C#, <br>vvD
|
|-
|-
| 52
| 52
Line 569: Line 516:
| down 8ve
| down 8ve
| vD
| vD
|
|-
|-
| 53
| 53
Line 578: Line 524:
| perfect 8ve
| perfect 8ve
| D
| D
|
|}
|}
<nowiki>*</nowiki> Based on interpreting 53edo as a no-17's [[19-limit]] temperament. Italics represent inconsistent intervals which are mapped by the 19-limit [[patent val]] to their second-best (as opposed to best) approximation in 53edo.
<nowiki>*</nowiki> Based on interpreting 53edo as a no-17's [[19-limit]] temperament. Italics represent inconsistent intervals which are mapped by the 19-limit [[patent val]] to their second-best (as opposed to best) approximation in 53edo.
Combining ups and downs notation with [[Kite's_color_notation|color notation]], qualities can be loosely associated with colors:
Combining ups and downs notation with [[color notation]], qualities can be loosely associated with colors:


{| class="wikitable center-all"
{| class="wikitable center-all"
Line 875: Line 820:
* [[List of edo-distinct 53et rank two temperaments]]
* [[List of edo-distinct 53et rank two temperaments]]
* [[Schismic-Mercator equivalence continuum]]
* [[Schismic-Mercator equivalence continuum]]
{| class="wikitable center-all left-5"
|+ Table of rank-2 temperaments by generator
|-
! Periods<br> per Octave
! Generator
! Cents
! Associated Ratio
! Temperament
|-
| 1
| 2\53
| 45.28
| 36/35
| [[Quartonic]]
|-
| 1
| 7\53
| 158.49
| 11/10
| [[Hemikleismic]]
|-
| 1
| 11\53
| 249.06
| 15/13
| [[Hemischis]]
|-
| 1
| 12\53
| 271.70
| 7/6
| [[Orson]] / [[orwell]]
|-
| 1
| 14\53
| 316.98
| 6/5
| [[Hanson]] / [[catakleismic]] / [[countercata]]
|-
| 1
| 15\53
| 339.62
| 11/9
| [[Amity]] / [[hitchcock]]
|-
| 1
| 19\53
| 430.19
| 9/7
| [[Hamity]]
|-
| 1
| 21\53
| 475.47
| 21/16
| [[Vulture]] / [[buzzard]]
|-
| 1
| 22\53
| 498.11
| 4/3
| [[Helmholtz]] / [[garibaldi]] / [[pontiac]]
|-
| 1
| 25\53
| 566.04
| 18/13
| [[Tricot]]
|}


== Music ==
== Music ==

Revision as of 09:15, 27 June 2021

← 52edo 53edo 54edo →
Prime factorization 53 is a prime
Step size 22.6415 ¢ 
Fifth 31\53 (701.887 ¢)
(convergent)
Semitones (A1:m2) 5:4 (113.2 ¢ : 90.57 ¢)
Consistency limit 9
Distinct consistency limit 9

The famous 53 equal division divides the octave into 53 equal comma-sized parts of around 22.6 cents each.

Theory

prime 2 prime 3 prime 5 prime 7 prime 11 prime 13 prime 17 prime 19 prime 23
Error absolute (¢) 0.00 -0.07 -1.41 +4.76 -7.92 -2.79 +8.26 -3.17 +5.69
relative (%) 0 -0 -6 +21 -35 -12 +36 -14 +25
Nearest edomapping 53 31 17 43 24 37 5 13 28
Fifthspan 0 +1 -8 -14 +23 +20 +7 -3 +18

53edo is notable as a 5-limit system, a fact apparently first noted by Isaac Newton, tempering out the schisma (32805/32768), the kleisma (15625/15552), the amity comma (1600000/1594323), the semicomma (2109375/2097152), and the vulture comma (10485760000/10460353203). In the 7-limit it tempers out 225/224, 1728/1715 and 3125/3087, the marvel comma, the gariboh, and the orwell comma. In the 11-limit, it tempers out 99/98 and 121/120, and is the optimal patent val for Big Brother temperament, which tempers out both, as well as 11-limit orwell temperament, which also tempers out the 11-limit comma 176/175. In the 13-limit, it tempers out 169/168, 275/273, 325/324, 540/539, 625/624, 676/675, and 2080/2079, and gives the optimal patent val for athene temperament. It is the seventh strict zeta edo and the 16th prime edo, following 47edo and coming before 59edo.

53edo has also found a certain dissemination as an EDO tuning for Arabic, Turkish, Persian music.

It can also be treated as a no-elevens, no-seventeens tuning, on which it is consistent all the way up to the 23-limit.

See also: Wikipedia: 53 equal temperament

Intervals

# Solfege Cents Approximate ratios* Ups and downs notation
0 do 0.00 1/1 P1 unison D
1 di 22.64 81/80, 64/63, 50/49 ^1 up unison ^D
2 daw 45.28 49/48, 36/35, 33/32, 128/125 ^^1,
vvm2 		double-up unison,
double-down minor 2nd 		^^D,
vvEb
3 ro 67.92 25/24, 28/27, 22/21, 27/26, 26/25 vm2 downminor 2nd vEb
4 rih 90.57 19/18, 20/19, 21/20, 256/243 m2 minor 2nd Eb
5 ra 113.21 16/15, 15/14 ^m2 upminor 2nd ^Eb
6 ru 135.85 14/13, 13/12, 27/25 v~2 downmid 2nd ^^Eb
7 ruh 158.49 12/11, 11/10, 57/52, 800/729 ^~2 upmid 2nd vvE
8 reh 181.13 10/9 vM2 downmajor 2nd vE
9 re 203.77 9/8 M2 major 2nd E
10 ri 226.42 8/7, 256/225 ^M2 upmajor 2nd ^E
11 raw 249.06 15/13, 144/125 ^^M2,
vvm3 		double-up major 2nd,
double-down minor 3rd 		^^E,
vvF
12 ma 271.70 7/6, 75/64 vm3 downminor 3rd vF
13 meh 294.34 13/11, 19/16, 32/27 m3 minor 3rd F
14 me 316.98 6/5 ^m3 upminor 3rd ^F
15 mu 339.62 11/9, 243/200 v~3 downmid 3rd ^^F
16 muh 362.26 16/13, 100/81 ^~3 upmid 3rd vvF#
17 mi 384.91 5/4 vM3 downmajor 3rd vF#
18 maa 407.55 19/15, 24/19, 81/64 M3 major 3rd F#
19 mo 430.19 9/7, 14/11 ^M3 upmajor 3rd ^F#
20 maw 452.83 13/10, 125/96 ^^M3,
vv4 		double-up major 3rd,
double-down 4th 		^^F#,
vvG
21 fe 475.47 21/16, 675/512, 320/243 v4 down 4th vG
22 fa 498.11 4/3 P4 perfect 4th G
23 fih 520.75 27/20 ^4 up 4th ^G
24 fu 543.40 11/8, 15/11, 26/19 v~4 downmid 4th ^^G
25 fuh 566.04 18/13 ^~4,
vd5 		upmid 4th,
downdim 5th 		vvG#,
vAb
26 fi 588.68 7/5, 45/32 vA4,
d5 		downaug 4th,
dim 5th 		vG#,
Ab
27 se 611.32 10/7, 64/45 A4,
^d5 		aug 4th,
updim 5th 		G#,
^Ab
28 suh 633.96 13/9 ^A4,
v~5 		upaug 4th,
downmid 5th 		^G#,
^^Ab
29 su 656.60 16/11, 19/13, 22/15 ^~5 upmid 5th vvA
30 sih 679.25 40/27 v5 down 5th vA
31 sol 701.89 3/2 P5 perfect 5th A
32 si 724.53 32/21, 243/160, 1024/675 ^5 up 5th ^A
33 saw 747.17 20/13, 192/125 ^^5,
vvm6 		double-up 5th,
double-down minor 6th 		^^A,
vvBb
34 lo 769.81 14/9, 25/16, 11/7 vm6 downminor 6th vBb
35 leh 792.45 19/12, 30/19, 128/81 m6 minor 6th Bb
36 le 815.09 8/5 ^m6 upminor 6th ^Bb
37 lu 837.74 13/8, 81/50 v~6 downmid 6th ^^Bb
38 luh 860.38 18/11, 400/243 ^~6 upmid 6th vvB
39 la 883.02 5/3 vM6 downmajor 6th vB
40 laa 905.66 22/13, 27/16, 32/19 M6 major 6th B
41 lo 928.30 12/7 ^M6 upmajor 6th ^B
42 law 950.94 26/15, 125/72 ^^M6,
vvm7 		double-up major 6th,
double-down minor 7th 		^^B,
vvC
43 ta 973.58 7/4 vm7 downminor 7th vC
44 teh 996.23 16/9 m7 minor 7th C
45 te 1018.87 9/5 ^m7 upminor 7th ^C
46 tu 1041.51 11/6, 20/11, 729/400 v~7 downmid 7th ^^C
47 tuh 1064.15 13/7, 24/13, 50/27 ^~7 upmid 7th vvC#
48 ti 1086.79 15/8 vM7 downmajor 7th vC#
49 tih 1109.43 19/10, 36/19, 40/21, 243/128 M7 major 7th C#
50 to 1132.08 48/25, 27/14, 21/11, 52/27, 25/13 ^M7 upmajor 7th ^C#
51 taw 1154.72 96/49, 35/18, 64/33, 125/64 ^^M7,
vv8 		double-up major 7th,
double-down 8ve 		^^C#,
vvD
52 da 1177.36 160/81, 63/32, 49/25 v8 down 8ve vD
53 do 1200.00 2/1 P8 perfect 8ve D

* Based on interpreting 53edo as a no-17's 19-limit temperament. Italics represent inconsistent intervals which are mapped by the 19-limit patent val to their second-best (as opposed to best) approximation in 53edo. Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

quality color monzo format examples
downminor zo (a, b, 0, 1) 7/6, 7/4
minor fourthward wa (a, b) with b < -1 32/27, 16/9
upminor gu (a, b, -1) 6/5, 9/5
downmid ilo (a, b, 0, 0, 1) 11/9, 11/6
upmid lu (a, b, 0, 0, -1) 12/11, 18/11
downmajor yo (a, b, 1) 5/4, 5/3
major fifthward wa (a, b) with b > 1 9/8, 27/16
upmajor ru (a, b, 0, -1) 9/7, 12/7

All 53edo chords can be named using ups and downs. An up, down or mid after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are.

Here are the zo, gu, ilo, lu, yo and ru triads:

color of the 3rd JI chord notes as edosteps notes of C chord written name spoken name
zo 6:7:9 0-12-31 C vEb G Cvm C downminor
gu 10:12:15 0-14-31 C ^Eb G C^m C upminor
ilo 18:22:27 0-15-31 C ^^Eb G Cv~ C downmid
lu 22:27:33 0-16-31 C vvE G C^~ C upmid
yo 4:5:6 0-17-31 C vE G Cv C downmajor or C down
ru 14:18:21 0-19-31 C ^E G C^ C upmajor or C up

For a more complete list, see Ups and Downs Notation #Chords and Chord Progressions.

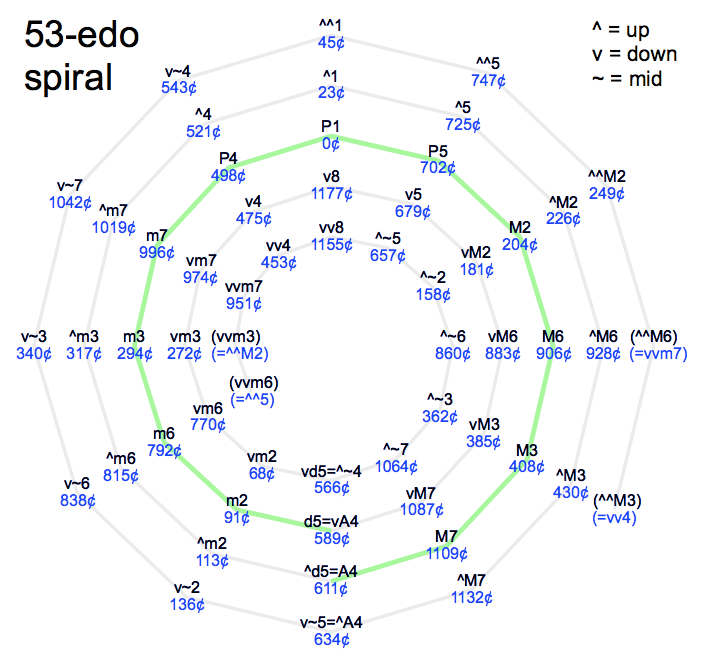
Relationship to 12-edo

Whereas 12-edo has a circle of twelve 5ths, 53-edo has a spiral of twelve 5ths (since 31\53 is on the 7\12 kite in the scale tree). This shows 53-edo in a 12-edo-friendly format. Excellent for introducing 53-edo to musicians unfamiliar with microtonal music. The two innermost and two outermost intervals on the spiral are duplicates.

JI approximation

53edo provides excellent approximations for the classic 5-limit just chords and scales, such as the Ptolemy-Zarlino "just major" scale.

interval ratio size difference
perfect fifth 3/2 31 −0.07 cents
major third 5/4 17 −1.40 cents
minor third 6/5 14 +1.34 cents
major tone 9/8 9 −0.14 cents
minor tone 10/9 8 −1.27 cents
diat. semitone 16/15 5 +1.48 cents

One notable property of 53EDO is that it offers good approximations for both just and Pythagorean major thirds.

The perfect fifth is almost perfectly equal to the just interval 3/2, with only a 0.07 cent difference! 53EDO is practically equal to an extended Pythagorean. The 14- and 17- degree intervals are also very close to 6/5 and 5/4 respectively, and so 5-limit tuning can also be closely approximated. In addition, the 43-degree interval is only 4.8 cents away from the just ratio 7/4, so 53EDO can also be used for 7-limit harmony, tempering out the septimal kleisma, 225/224.

15-odd-limit interval mappings

The following table shows how 15-odd-limit intervals are represented in 53edo. Octave-reduced prime harmonics are bolded; inconsistent intervals are in italic.

Interval, complement Error (abs, ¢)
4/3, 3/2 0.068
9/8, 16/9 0.136
10/9, 9/5 1.272
15/13, 26/15 1.316
6/5, 5/3 1.340
13/10, 20/13 1.384
5/4, 8/5 1.408
16/15, 15/8 1.476
18/13, 13/9 2.655
13/12, 24/13 2.724
16/13, 13/8 2.792
8/7, 7/4 4.759
7/6, 12/7 4.827
9/7, 14/9 4.895
13/11, 22/13 5.130
7/5, 10/7 6.167
15/14, 28/15 6.235
15/11, 22/15 6.445
11/10, 20/11 6.514
14/13, 13/7 7.551
11/9, 18/11 7.785
12/11, 11/6 7.854
11/8, 16/11 7.922
14/11, 11/7 9.961

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-84 53⟩ [⟨53 84]] +0.022 0.022 0.10
2.3.5 15625/15552, 32805/32768 [⟨53 84 123]] +0.216 0.276 1.22
2.3.5.7 225/224, 1728/1715, 3125/3087 [⟨53 84 123 149]] -0.262 0.861 3.81
2.3.5.7.11 99/98, 121/120, 176/175, 2200/2187 [⟨53 84 123 149 183]] +0.248 1.279 5.64
2.3.5.7.11.13 99/98, 121/120, 169/168, 176/175, 275/273 [⟨53 84 123 149 183 196]] +0.332 1.183 5.22
2.3.5.7.11.13.19 99/98, 121/120, 169/168, 176/175, 209/208, 275/273 [⟨53 84 123 149 183 196 225]] +0.391 1.105 4.88

53et is lower in relative error than any previous equal temperaments in the 3-, 5-, and 13-limit. The next ETs better in these subgroups are 306, 118, and 58, respectively. It is even more prominent in the 2.3.5.7.13.19 and 2.3.5.7.13.19.23 subgroups, and the next ET better in either subgroup is 130.

Linear temperaments

Table of rank-2 temperaments by generator
Periods
per Octave 		Generator Cents Associated Ratio Temperament
1 2\53 45.28 36/35 Quartonic
1 7\53 158.49 11/10 Hemikleismic
1 11\53 249.06 15/13 Hemischis
1 12\53 271.70 7/6 Orson / orwell
1 14\53 316.98 6/5 Hanson / catakleismic / countercata
1 15\53 339.62 11/9 Amity / hitchcock
1 19\53 430.19 9/7 Hamity
1 21\53 475.47 21/16 Vulture / buzzard
1 22\53 498.11 4/3 Helmholtz / garibaldi / pontiac
1 25\53 566.04 18/13 Tricot

Music

Retrieved from "https://en.xen.wiki/index.php?title=53edo&oldid=73279"