Miracle: Difference between revisions
added 103edo and 113edo |
m →Music: cleanup |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[de:Miracle]] | [[de:Miracle]] | ||
{{Wikipedia|Miracle temperament}} | {{Wikipedia|Miracle temperament}} | ||
'''Miracle''' is a [[regular temperament]] discovered by [[George Secor]] in 1974 which | '''Miracle''' is a [[regular temperament]] discovered by [[George Secor]] in 1974 which splits a tempered [[3/2]] into six [[generator]]s, called ''[[secor]]s'' (after George), that serve as both [[15/14]] and [[16/15]] semitones. A stack of two generators represents [[8/7]], and a stack of seven generators represents [[8/5]]. It is a member of both the [[marvel temperaments]], by [[tempering out]] [[225/224]], and the [[gamelismic clan]], by tempering out [[1029/1024]]. It extends naturally to the [[11-limit]] by treating the neutral third from three generators as [[11/9]], tempering out [[243/242]], [[385/384]], [[441/440]], and [[540/539]]. | ||
Miracle is an exceptionally efficient linear temperament | Miracle is an exceptionally efficient linear temperament. It is quite accurate, with [[TOP]] error only 0.63 [[cent]]s/[[octave]], meaning intervals of the [[11-odd-limit]] [[tonality diamond]] are represented with only one or two cents of error. Yet it is also very low-complexity (efficient), as evidenced by the high density of 11-odd-limit ratios in the [[#Interval chain]]. At least one inversion of every interval in the 11-odd-limit tonality diamond is represented within 22 secors of the starting value. | ||
Some temperaments have | Some temperaments have 11/9 as a neutral third, meaning it is exactly half of a 3/2 (tempering out 243/242), and other temperaments have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts. | ||
Miracle can also be thought of as a [[cluster temperament]] with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing [[45/44]] ~ [[49/48]] ~ [[50/49]] ~ [[55/54]] ~ [[56/55]] ~ [[64/63]] all [[tempered]] together. | Miracle can also be thought of as a [[cluster temperament]] with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing [[45/44]] ~ [[49/48]] ~ [[50/49]] ~ [[55/54]] ~ [[56/55]] ~ [[64/63]] all [[tempered]] together. | ||
See [[Miracle extensions]] for [[13-limit]] and [[17-limit]] extensions. See [[Gamelismic clan #Miracle]] for technical data. | |||
== Interval chain == | == Interval chain == | ||
| Line 181: | Line 181: | ||
=== Prime-optimized tunings === | === Prime-optimized tunings === | ||
{| class="wikitable mw-collapsible mw-collapsed" | {| class="wikitable mw-collapsible mw-collapsed" | ||
|+ style="font-size: 105%; white-space: nowrap;" | 7-limit Prime- | |+ style="font-size: 105%; white-space: nowrap;" | 7-limit Prime-optimized tunings | ||
|- | |- | ||
! rowspan="2" | | ! rowspan="2" | | ||
! colspan="2" | Euclidean | ! colspan="2" | Euclidean | ||
|- | |- | ||
! | ! Constrained | ||
! | ! Constrained & skewed | ||
|- | |- | ||
! Equilateral | ! Equilateral | ||
| CEE: ~15/14 = 116. | | CEE: ~15/14 = 116.516{{c}} | ||
| CSEE: ~15/14 = 116. | | CSEE: ~15/14 = 116.561{{c}} | ||
|- | |- | ||
! Tenney | ! Tenney | ||
| CTE: ~15/14 = 116. | | CTE: ~15/14 = 116.677{{c}} | ||
| CWE: ~15/14 = 116. | | CWE: ~15/14 = 116.676{{c}} | ||
|- | |- | ||
! Benedetti, <br>Wilson | ! Benedetti, <br>Wilson | ||
| CBE: ~15/14 = 116. | | CBE: ~15/14 = 116.730{{c}} | ||
| CSBE: ~15/14 = 116. | | CSBE: ~15/14 = 116.714{{c}} | ||
|} | |} | ||
{| class="wikitable mw-collapsible mw-collapsed" | {| class="wikitable mw-collapsible mw-collapsed" | ||
|+ style="font-size: 105%; white-space: nowrap;" | 11-limit | |+ style="font-size: 105%; white-space: nowrap;" | 11-limit prime-optimized tunings | ||
|- | |- | ||
! rowspan="2" | | ! rowspan="2" | | ||
! colspan="2" | Euclidean | ! colspan="2" | Euclidean | ||
|- | |- | ||
! | ! Constrained | ||
! | ! Constrained & skewed | ||
|- | |- | ||
! Equilateral | ! Equilateral | ||
| CEE: ~15/14 = 116. | | CEE: ~15/14 = 116.687{{c}} | ||
| CSEE: ~15/14 = 116. | | CSEE: ~15/14 = 116.630{{c}} | ||
|- | |- | ||
! Tenney | ! Tenney | ||
| CTE: ~15/14 = 116. | | CTE: ~15/14 = 116.711{{c}} | ||
| CWE: ~15/14 = 116. | | CWE: ~15/14 = 116.647{{c}} | ||
|- | |- | ||
! Benedetti, <br>Wilson | ! Benedetti, <br>Wilson | ||
| CBE: ~15/14 = 116. | | CBE: ~15/14 = 116.736{{c}} | ||
| CSBE: ~15/14 = 116. | | CSBE: ~15/14 = 116.677{{c}} | ||
|} | |||
=== Target tunings === | |||
{| class="wikitable center-all mw-collapsible mw-collapsed" | |||
|+ style="white-space: nowrap;" | Minimax tunings | |||
|- | |||
! Target | |||
! Generator | |||
! Eigenmonzo* | |||
|- | |||
| 5-odd-limit | |||
| ~16/15 = 116.588{{c}} | |||
| 5/3 | |||
|- | |||
| 7-odd-limit | |||
| ~15/14 = 116.588{{c}} | |||
| 5/3 | |||
|- | |||
| 9-odd-limit | |||
| ~15/14 = 116.716{{c}} | |||
| 9/5 | |||
|- | |||
| 11-odd-limit | |||
| ~15/14 = 116.716{{c}} | |||
| 9/5 | |||
|} | |||
{| class="wikitable center-all left-3 mw-collapsible mw-collapsed" | |||
|+ style="white-space: nowrap;" | Least squares tunings | |||
|- | |||
! Target | |||
! Generator | |||
! Eigenmonzo* | |||
|- | |||
| 5-odd-limit | |||
| ~16/15 = 116.578{{c}} | |||
| {{Monzo| 0 -19 20 }} | |||
|- | |||
| 7-odd-limit | |||
| ~15/14 = 116.573{{c}} | |||
| {{Monzo| 0 -27 25 5 }} | |||
|- | |||
| 9-odd-limit | |||
| ~15/14 = 116.721{{c}} | |||
| {{Monzo| 0 117 -44 -19 }} | |||
|- | |||
| 11-odd-limit | |||
| ~15/14 = 116.672{{c}} | |||
| {{Monzo| 0 17 -11 -6 11 }} | |||
|} | |} | ||
| Line 228: | Line 277: | ||
|- | |- | ||
! Edo<br>generator | ! Edo<br>generator | ||
! [[Eigenmonzo| | ! [[Eigenmonzo|Unchanged interval<br>(eigenmonzo)]]* | ||
! Generator (¢) | ! Generator (¢) | ||
! Comments | ! Comments | ||
| Line 281: | Line 330: | ||
| 116.505 | | 116.505 | ||
| | | | ||
|- | |- | ||
| | | | ||
| Line 321: | Line 360: | ||
| 116.667 | | 116.667 | ||
| | | | ||
|- | |- | ||
| | | | ||
| Line 331: | Line 365: | ||
| 116.716 | | 116.716 | ||
| 9- and 11-odd-limit minimax, <br>Secor's definition of secor | | 9- and 11-odd-limit minimax, <br>Secor's definition of secor | ||
|- | |- | ||
| | | | ||
| Line 382: | Line 411: | ||
| Upper bound of 7- and 9-odd-limit diamond monotone | | Upper bound of 7- and 9-odd-limit diamond monotone | ||
|} | |} | ||
<nowiki/>* Besides the octave | |||
== Music == | == Music == | ||
; [[Herman Miller]] | ; [[Herman Miller]] | ||
* [https://soundcloud.com/morphosyntax-1/realm-of-possibility ''Realm of Possibility''] (2021) – Miracle[31] with a 116.72-cent generator and 1200.53-cent octave | * [https://soundcloud.com/morphosyntax-1/realm-of-possibility ''Realm of Possibility''] (2021) – in Miracle[31] with a 116.72-cent generator and 1200.53-cent octave | ||
; [[Joseph Pehrson]] | ; [[Joseph Pehrson]] | ||
* ''Blackjack'' (2001) – [https://web.archive.org/web/20201127013023/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blackjack.mp3 play] | [https://soundclick.com/share.cfm?id=706344 SoundClick] – [[Blackjack|Blackjack (Miracle{{lbrack}}21{{rbrack}})]] | * ''Blackjack'' (2001) – [https://web.archive.org/web/20201127013023/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blackjack.mp3 play] | [https://soundclick.com/share.cfm?id=706344 SoundClick] – in [[Blackjack|Blackjack (Miracle{{lbrack}}21{{rbrack}})]] | ||
* ''Blacklight'' (2002) – [https://web.archive.org/web/20201127015033/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blacklight.mp3 play] | [https://soundclick.com/share.cfm?id=710783 SoundClick] – Blackjack (Miracle[21]) | * ''Blacklight'' (2002) – [https://web.archive.org/web/20201127015033/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blacklight.mp3 play] | [https://soundclick.com/share.cfm?id=710783 SoundClick] – in Blackjack (Miracle[21]) | ||
* ''Black and Jill'' (2003) – Blackjack (Miracle[21]) | * ''Black and Jill'' (2003) – in Blackjack (Miracle[21]) | ||
** Soprano version – [https://web.archive.org/web/20201127012730/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/blackandjill.mp3 play] | [https://soundclick.com/share.cfm?id=2373400 SoundClick] | ** Soprano version – [https://web.archive.org/web/20201127012730/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/blackandjill.mp3 play] | [https://soundclick.com/share.cfm?id=2373400 SoundClick] | ||
** [https://soundclick.com/share.cfm?id=9583778 Udderbot version] | ** [https://soundclick.com/share.cfm?id=9583778 Udderbot version] | ||
* [https://soundclick.com/share.cfm?id=2623155 ''Inner Voices''] (2005) – Blackjack (Miracle[21]) | * [https://soundclick.com/share.cfm?id=2623155 ''Inner Voices''] (2005) – in Blackjack (Miracle[21]) | ||
* [https://soundclick.com/share.cfm?id=6593353 ''Transpian''] (2006) – Blackjack (Miracle[21]) | * [https://soundclick.com/share.cfm?id=6593353 ''Transpian''] (2006) – in Blackjack (Miracle[21]) | ||
* [https://soundclick.com/share.cfm?id=5049231 ''microproj''] (2007) – Blackjack (Miracle[21]) | * [https://soundclick.com/share.cfm?id=5049231 ''microproj''] (2007) – in Blackjack (Miracle[21]) | ||
; [[Gene Ward Smith]] | ; [[Gene Ward Smith]] | ||
* ''Rachmaninoff Plays Blackjack'' (archived 2010) – [http://www.archive.org/details/RachmaninoffPlaysBlackjack detail] | [http://www.archive.org/download/RachmaninoffPlaysBlackjack/rachman.mp3 play] – Blackjack (Miracle[21] | * ''Rachmaninoff Plays Blackjack'' (archived 2010) – [http://www.archive.org/details/RachmaninoffPlaysBlackjack detail] | [http://www.archive.org/download/RachmaninoffPlaysBlackjack/rachman.mp3 play] – in Blackjack (Miracle[21]), 175edo tuning | ||
[[Category:Miracle| ]] <!-- main article --> | [[Category:Miracle| ]] <!-- main article --> | ||
[[Category:Rank-2 temperaments]] | |||
[[Category:Marvel temperaments]] | [[Category:Marvel temperaments]] | ||
[[Category:Gamelismic clan]] | [[Category:Gamelismic clan]] | ||
Latest revision as of 11:53, 26 July 2025
Miracle is a regular temperament discovered by George Secor in 1974 which splits a tempered 3/2 into six generators, called secors (after George), that serve as both 15/14 and 16/15 semitones. A stack of two generators represents 8/7, and a stack of seven generators represents 8/5. It is a member of both the marvel temperaments, by tempering out 225/224, and the gamelismic clan, by tempering out 1029/1024. It extends naturally to the 11-limit by treating the neutral third from three generators as 11/9, tempering out 243/242, 385/384, 441/440, and 540/539.
Miracle is an exceptionally efficient linear temperament. It is quite accurate, with TOP error only 0.63 cents/octave, meaning intervals of the 11-odd-limit tonality diamond are represented with only one or two cents of error. Yet it is also very low-complexity (efficient), as evidenced by the high density of 11-odd-limit ratios in the #Interval chain. At least one inversion of every interval in the 11-odd-limit tonality diamond is represented within 22 secors of the starting value.
Some temperaments have 11/9 as a neutral third, meaning it is exactly half of a 3/2 (tempering out 243/242), and other temperaments have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts.
Miracle can also be thought of as a cluster temperament with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing 45/44 ~ 49/48 ~ 50/49 ~ 55/54 ~ 56/55 ~ 64/63 all tempered together.
See Miracle extensions for 13-limit and 17-limit extensions. See Gamelismic clan #Miracle for technical data.
Interval chain
In the following table, odd harmonics and subharmonics 1–21 are labeled in bold.
| # | Cents* | Approximate ratios |
|---|---|---|
| 0 | 0.0 | 1/1 |
| 1 | 116.6 | 15/14, 16/15 |
| 2 | 233.3 | 8/7 |
| 3 | 349.9 | 11/9 |
| 4 | 466.6 | 21/16 |
| 5 | 583.2 | 7/5 |
| 6 | 699.9 | 3/2 |
| 7 | 816.5 | 8/5 |
| 8 | 933.2 | 12/7 |
| 9 | 1049.8 | 11/6 |
| 10 | 1166.5 | 49/25, 55/28, 63/32, 88/45, 96/49, 108/55 |
| 11 | 83.1 | 21/20, 22/21 |
| 12 | 199.8 | 9/8 |
| 13 | 316.4 | 6/5 |
| 14 | 433.1 | 9/7 |
| 15 | 549.7 | 11/8 |
| 16 | 666.3 | 22/15 |
| 17 | 783.0 | 11/7 |
| 18 | 899.6 | 27/16, 42/25 |
| 19 | 1016.3 | 9/5 |
| 20 | 1132.9 | 27/14, 48/25 |
| 21 | 49.6 | 33/32, 36/35 |
| 22 | 166.2 | 11/10 |
| 23 | 282.9 | 33/28 |
| 24 | 399.5 | 44/35 |
| 25 | 516.2 | 27/20 |
| 26 | 632.8 | 36/25 |
| 27 | 749.5 | 54/35, 77/50 |
| 28 | 866.1 | 33/20 |
| 29 | 982.8 | 44/25 |
| 30 | 1099.4 | 66/35 |
| 31 | 16.1 | 81/80, 99/98, 121/120 |
* In 11-limit CWE tuning, octave reduced
Chords
Scales
- Mos scales
- Miracle[10] – 72edo tuning
- Blackjack (miracle[21]) – 72edo tuning
- Blackwoo
- Transversal scales
- Others
- Mir1 – 6-tone scale, 72edo tuning
- Mir2 – 6-tone scale, 72edo tuning
- Miracle 8 – 8-tone scale, 72edo tuning
- Miracle 12 – 12-tone scale, 72edo tuning
- Miracle 12a – 12-tone scale, 72edo tuning
- Miracle 24hi – 24-tone scale, 72edo tuning
- Miracle 24lo – 24-tone scale, 72edo tuning
Tunings
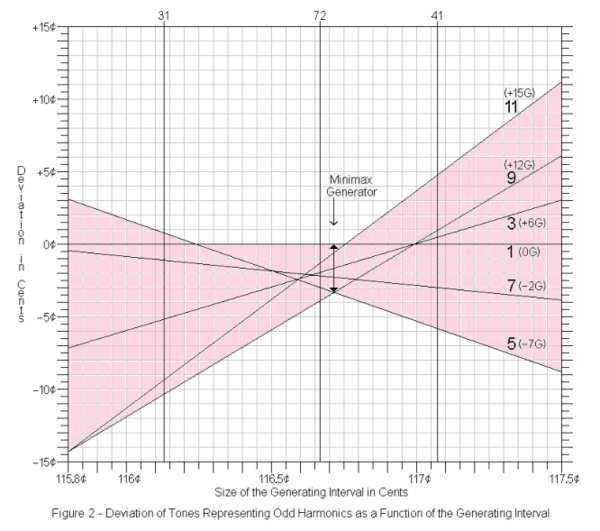
Displayed on the right is a chart of the tuning spectrum of miracle by how the odd harmonics up to 11 are tuned, showing the minimax generator, i.e. the secor.
Prime-optimized tunings
| Euclidean | ||
|---|---|---|
| Constrained | Constrained & skewed | |
| Equilateral | CEE: ~15/14 = 116.516 ¢ | CSEE: ~15/14 = 116.561 ¢ |
| Tenney | CTE: ~15/14 = 116.677 ¢ | CWE: ~15/14 = 116.676 ¢ |
| Benedetti, Wilson |
CBE: ~15/14 = 116.730 ¢ | CSBE: ~15/14 = 116.714 ¢ |
| Euclidean | ||
|---|---|---|
| Constrained | Constrained & skewed | |
| Equilateral | CEE: ~15/14 = 116.687 ¢ | CSEE: ~15/14 = 116.630 ¢ |
| Tenney | CTE: ~15/14 = 116.711 ¢ | CWE: ~15/14 = 116.647 ¢ |
| Benedetti, Wilson |
CBE: ~15/14 = 116.736 ¢ | CSBE: ~15/14 = 116.677 ¢ |
Target tunings
| Target | Generator | Eigenmonzo* |
|---|---|---|
| 5-odd-limit | ~16/15 = 116.588 ¢ | 5/3 |
| 7-odd-limit | ~15/14 = 116.588 ¢ | 5/3 |
| 9-odd-limit | ~15/14 = 116.716 ¢ | 9/5 |
| 11-odd-limit | ~15/14 = 116.716 ¢ | 9/5 |
| Target | Generator | Eigenmonzo* |
|---|---|---|
| 5-odd-limit | ~16/15 = 116.578 ¢ | [0 -19 20⟩ |
| 7-odd-limit | ~15/14 = 116.573 ¢ | [0 -27 25 5⟩ |
| 9-odd-limit | ~15/14 = 116.721 ¢ | [0 117 -44 -19⟩ |
| 11-odd-limit | ~15/14 = 116.672 ¢ | [0 17 -11 -6 11⟩ |
Tuning spectrum
| Edo generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 15/8 | 111.731 | ||
| 2\21 | 114.286 | Lower bound of 7-odd-limit diamond monotone | |
| 7/4 | 115.587 | ||
| 11/9 | 115.803 | ||
| 3\31 | 116.129 | Lower bound of 9- and 11-odd-limit, 11-limit 15- and 21-odd-limit diamond monotone | |
| 5/4 | 116.241 | ||
| 21/11 | 116.412 | ||
| 15/11 | 116.441 | ||
| 7/5 | 116.502 | ||
| 10\103 | 116.505 | ||
| 5/3 | 116.588 | 5- and 7-odd-limit minimax | |
| 11/10 | 116.591 | ||
| 11/6 | 116.596 | ||
| 11/7 | 116.617 | ||
| 7/6 | 116.641 | ||
| 7\72 | 116.667 | ||
| 9/5 | 116.716 | 9- and 11-odd-limit minimax, Secor's definition of secor | |
| 11/8 | 116.755 | ||
| 21/20 | 116.770 | ||
| 9/7 | 116.792 | ||
| 11\113 | 116.814 | ||
| 3/2 | 116.993 | ||
| 4\41 | 117.073 | Upper bound of 11-odd-limit, 11-limit 15- and 21-odd-limit diamond monotone | |
| 21/16 | 117.695 | ||
| 15/14 | 119.443 | ||
| 1\10 | 120.000 | Upper bound of 7- and 9-odd-limit diamond monotone |
* Besides the octave
Music
- Realm of Possibility (2021) – in Miracle[31] with a 116.72-cent generator and 1200.53-cent octave
- Blackjack (2001) – play | SoundClick – in Blackjack (Miracle[21])
- Blacklight (2002) – play | SoundClick – in Blackjack (Miracle[21])
- Black and Jill (2003) – in Blackjack (Miracle[21])
- Soprano version – play | SoundClick
- Udderbot version
- Inner Voices (2005) – in Blackjack (Miracle[21])
- Transpian (2006) – in Blackjack (Miracle[21])
- microproj (2007) – in Blackjack (Miracle[21])
