Secor

English Wikipedia has an article on:

Secor (interval)

The secor is a unit of interval size named after George Secor. It's original technical definition is (18/5)^1/19, or 116.716 ¢, the 11-limit minimax generator for miracle temperament, but it can be used for any interval of similar size that fulfils the requirements for Miracle and its extensions.

The secor was first derived by George Secor in 1975, in his article "A new look at the Partch Monophonic Fabric", published in Xenharmonikôn 3: "If the above keyboard is tuned so that each key plays 116.89 cents different in pitch from the one beside it, a temperament will result in which none of the 29 primary ratios within the 11-limit will be more than about 3.32 cents false." At this time, the interval was yet unnamed. The name "secor" was proposed in 2001 by Dave Keenan, both in honor of Secor and as a contraction of "SECond, minOR".

For more information, see: http://anaphoria.com/SecorMiracle.pdf

A diagram taken from George Secor's article "The Miracle Temperament and Decimal Keyboard" which was published in Xenharmonikôn 18 (2006). This version includes minor revisions for clarity, done by Douglas Blumeyer on Dave Keenan's request.

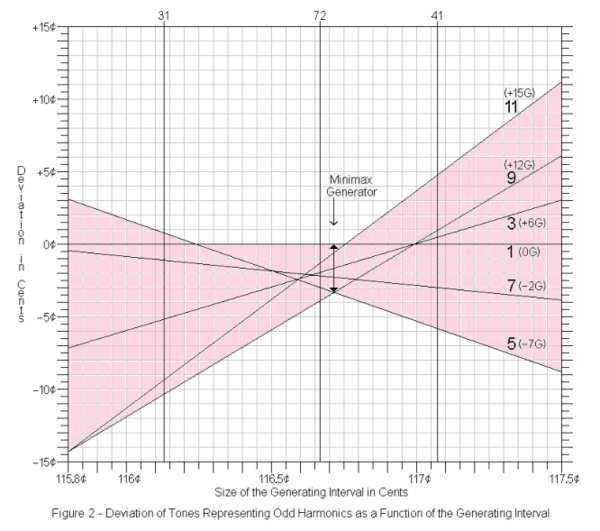
This diagram visually demonstrates how the secor is found as the interval that nearly-equally subdivides all six of the smallest odd harmonics — 1, 3, 5, 7, 9, and 11 — where the width of the error band is narrowest, thus minimizing the maximum error of any interval in the 11-odd-limit tonality diamond.

Note that the method here is not to minimize the absolute deviation from 0 ¢ in each harmonic individually, but to minimize the relative difference between the errors of the harmonic with the greatest positive error and the harmonic with the greatest negative error. In other words, the method is not to minimize the maximum distance of the diagonal harmonic lines from the horizontal 0 ¢ axis, but to minimize the width of the band between the highest harmonic line and the lowest harmonic line at any given vertical slice through the chart.

Interestingly, the case of the secor, both methods would happen to give the same result. This is because at the point where the difference in errors of the harmonic is least here, all errors are non-positive. So the odd harmonic with the most positive error is actually 1, with an error of 0 ¢, because it is purely tuned of course, and therefore its harmonic line is identical with the horizontal 0 ¢ axis. And the odd harmonic with the most negative error is a tie between 5 and 9, both of which have an error of -3.323 ¢.

See also

• 19ed18/5 - equal-step nonoctave tuning based on the secor interval