MOS scale family tree
The MOS scale family tree (or mos family tree) is an infinite binary tree that organizes moment-of-symmetry scales based on the parent-to-child relationship between scales. This tree is not to be confused with other scale trees, such as those based on the Stern-Brocot or tree or Farey tree. Rather, this tree organizes MOS scales quite differently, depicting a family tree of step patterns.
History
Erv Wilson was the first to describe such a tree using Fibonacci rabbit patterns. One version of his tree is referred to the scale/rhythm tree, and it's this tree that shows the parent-child relationship between all (single-period) moment-of-symmetry scales.
Since the term "scale tree" is already used to describe scales arranged using the Farey or Stern-Brocot trees, the term "family tree" is used instead.
Conventions and other differences
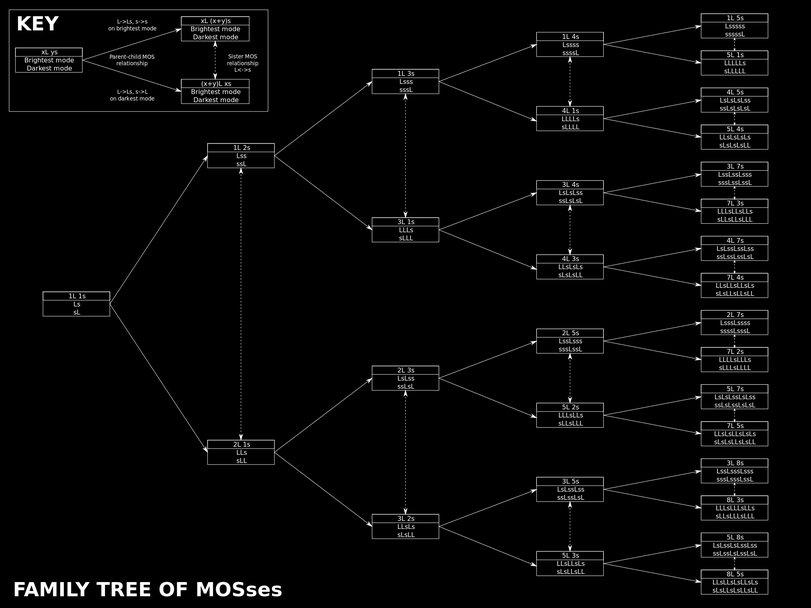
For the purposes of this article, the mos family tree will be depicted sideways and with an "upper" and "lower" child mos, rather than a left and right child, as typical with binary trees. This is exactly how Wilson initially described his tree, but with a few additional differences, listed below:
- Scale step patterns may not be shown; preferably, the mos in its xL ys form will be shown instead of a step pattern.
- If step patterns are shown, they will always be shown in both its brightest and darkest modes.
- The construction rules described here result in a tree that is upside-down relative to Wilson's description.
Construction
At the root of the tree is the step pattern Ls, representing the mos 1L 1s. The child scales of any node can be constructed as such:
- One child (the upper child) starts with a copy of the step pattern of its parent and has every "L" replaced with "Ls" and every "s" is replaced with "s".
- The other child (the lower child) starts with a reversed copy of the parent's step pattern and has every "L" replaced with "Ls" and every "s" replaced with "L".
This pattern is repeated indefinitely to each new node added to the tree, or for however many generations are desired.
An alternate version of the tree can be made by only considering the number of steps there are, ignoring the pattern of steps formed. Again, the tree starts with 1L 1s at the root. The child scales will have the following note counts, given a parent of xL ys:
- One child will have x large steps and x+y small steps, for a mos of xL (x+y)s.
- The other child will have x+y large steps and x small steps, for a mos of (x+y)L xs.
Family tree as a table
The following table organizes mosses as described. Scales with at least 4 steps have links that go to their corresponding page.
| Parent Scale | 1st-order child mosses | 2nd-order child mosses | 3rd-order child mosses | 4th-order child mosses | 5th-order child mosses |
|---|---|---|---|---|---|
| 1L 1s | 1L 2s | 1L 3s | 1L 4s | 1L 5s | 1L 6s |
| 6L 1s | |||||
| 5L 1s | 5L 6s | ||||
| 6L 5s | |||||
| 4L 1s | 4L 5s | 4L 9s | |||
| 9L 4s | |||||
| 5L 4s | 5L 9s | ||||
| 9L 5s | |||||
| 3L 1s | 3L 4s | 3L 7s | 3L 10s | ||
| 10L 3s | |||||
| 7L 3s | 7L 10s | ||||
| 10L 7s | |||||
| 4L 3s | 4L 7s | 4L 11s | |||
| 11L 4s | |||||
| 7L 4s | 7L 11s | ||||
| 11L 7s | |||||
| 2L 1s | 2L 3s | 2L 5s | 2L 7s | 2L 9s | |
| 9L 2s | |||||
| 7L 2s | 7L 9s | ||||
| 9L 7s | |||||
| 5L 2s | 5L 7s | 5L 12s | |||
| 12L 5s | |||||
| 7L 5s | 7L 12s | ||||
| 12L 7s | |||||
| 3L 2s | 3L 5s | 3L 8s | 3L 11s | ||
| 11L 3s | |||||
| 8L 3s | 8L 11s | ||||
| 11L 8s | |||||
| 5L 3s | 5L 8s | 5L 13s | |||
| 13L 5s | |||||
| 8L 5s | 8L 13s | ||||
| 13L 8s |
Observations
The following section is a list of observations that are either mathematical or can be made with respect to other structures described by various xenharmonic theories.
Growth
The uppermost branch in the tree experiences linear growth, growing by one step each generation, and the lowermost branch experiences exponential growth, in line with the Fibonacci sequence.
Relation to temperaments
Since a tree structure is built such that each node connects back to a unique parent (except for the root), there are no looping paths, so every path between any two nodes is unique. In regular temperament theory, scales are described as being generated from stacking an interval repeatedly, with moment-of-symmetry scales resulting from this process. Since the sizes of the generating intervals are necessarily described, this means temperaments describe a specific path down the family tree.
Relation to EDOs
Since every interval available to an EDO can be used as a generating interval, repeatedly stacking such an interval will necessarily produce mosses. Each mos produced this way will describe a unique path on the mos family tree, starting at 1L 1s and terminating right before a pair of sister scales whose note count is equal to the number of equal divisions. Combining all of these paths into a tree will form a subset of the infinite mos family tree, where each path represents a different sequence of mosses that all have the same generating intervals.
External links
Stern-Brocot Tree on Wikipedia