Andrew Heathwaite's MOS Investigations
This is a page for me, Andrew Heathwaite, to organize my thoughts and questions regarding Moment of Symmetry Scales. I'm using it primarily to provoke and organize conversations with myself. It's a sort of personal sandbox. If it provokes conversations with others, all the better! You *yes you* are more than welcome to correct obvious errors, add clearly-demarked related material, and comment through the comments tab -- ask questions, tell me where you think I'm totally bonkers, connect me to similar ideas that you may know about, give a hurrah or two -- whatever you find suitable.
Map of Sensi[8]
This diagram is an experiment in combining the two ways I tend to visualize MOS scales -- as a chain of generators (x-axis) and as particular steps in pitch-space (y-axis).
An Approach to Chromatic/Enharmonic MODMOS Scales
I am new to this and may be reinventing wheels. If you have anything to add or correct, please comment!
MODMOS Scales generalize the class of scales which are not MOS, but which have been obtained by applying a finite number of chromatic alterations to an MOS. In particular, the chromatic alterations are (usually) by "chroma," a small interval obtained by subtracting s from L. (c = L-s.) With strictly proper MOS Scales (which have 2s > L), the chroma is smaller than s (s > L-s). These are the scales I've been looking at recently. I have found that the MODMOS procedure produces interesting and useful scales in sensi[8] and miracle[10], as well as porcupine[7].
Mike Battaglia, whose enthusiastic promotion of the MODMOS scales of porcupine[7] has informed and inspired me, has proposed two new letters to stand for altered steps of MODMOS scales. "A" (short for "augmented") is a large step which has been widened by one chroma. (A = L+c.) Likewise, "d" (short for "diminished") is a small step which has been narrowed by one chroma. (d = s-c.) Thus, a MODMOS scale can be written like LsdLsss. I noticed that d and c can serve as "atoms" for deriving the other three steps, as follows:
d = d
s = d+c
L = s+c = d+c+c = d+2c
A = L+c = d+c+c+c = d+3c
Notice that the chroma is not a step in its own right. This is particularly significant in these strictly-proper MOS scales, since the chroma is the smallest interval that is used.
It may be useful to take subsets of larger MODMOS scales. In this case, it is likely that a 2-step interval will be taken as a single step in the subset scale. Of course, so could a 3-step interval and so on, but for now I'm looking at the 2-step intervals. Since the steps in our parent scale can be any of four varieties, we have the following possible 2-steps:
dd = d+d = 2d
sd = d+c+d = 2d+c
ss = d+c+d+c = 2d+2c
Ld = d+c+c+d = 2d+2c
Ls = d+c+c+d+c = 2d+3c
Ad = d+c+c+c+d = 2d+3c
LL = d+c+c+d+c+c = 2d+4c
As = d+c+c+c+d+c = 2d+4c
AL = d+c+c+c+d+c+c = 2d+5c
AA = d+c+c+c+d+c+c+c = 2d+6c
Notice that ss=Ld, Ls=Ad, and LL=As. These equalities are always going to be true, as you can see by converting the steps into d's and c's. Other equalities may pop up, depending on the size of d and c -- we'll see that in our porcupine[7] examples below.
Here is a chart showing all of the possible 1-steps and 2-steps in sensi[8] MODMOSes in 46edo and miracle[10] MODMOSes in 72edo. You can see that a lot more variety is available here than in a straight MOS scale.
| step | type |
|
|
degrees of sensi[8] | cents value | degrees of miracle[10] | cents value |
|---|---|---|---|---|---|---|---|
| * | * | * | * | * | * | * | * |
| c | chroma | 0 | 1 | 2 | 52 | 2 | 33 |
| * | * | * | * | * | * | * | * |
| d | 1-step | 1 | 0 | 3 | 78 | 5 | 83 |
| s | 1-step | 1 | 1 | 5 | 130 | 7 | 117 |
| L | 1-step | 1 | 2 | 7 | 183 | 9 | 150 |
| A | 1-step | 1 | 3 | 9 | 235 | 11 | 183 |
| * | * | * | * | * | * | * | * |
| dd | 2-step | 2 | 0 | 6 | 157 | 10 | 167 |
| sd | 2-step | 2 | 1 | 8 | 209 | 12 | 200 |
| ss=Ld | 2-step | 2 | 2 | 10 | 261 | 14 | 233 |
| Ls=Ad | 2-step | 2 | 3 | 12 | 313 | 16 | 267 |
| LL=As | 2-step | 2 | 4 | 14 | 365 | 18 | 300 |
| AL | 2-step | 2 | 5 | 16 | 417 | 20 | 333 |
| AA | 2-step | 2 | 6 | 18 | 470 | 22 | 367 |
In these examples, the largest 1-steps are larger than the smallest 2-steps, showing that a MODMOS scale of a proper MOS scale will not necessarily be proper. While a MODMOS scale may contain this variety of steps, it also may not. MODMOS scales sometimes produce permutations of the steps of the original MOS, in which case no diminished or augmented intervals appear at all. Thus, this chart is showing the maximum possible variety in 1-steps and 2-steps in sensi[8] and miracle[10] MODMOSes.
In playing around with these scales, I found that the sensi[8] MODMOSes sound like albitonic (approximately diatonic-sized) scales -- 8 is not too far off from 7. I also found it pretty easy to distinguish the different types of steps.
I found it more natural with miracle[10] MODMOSes, to take subsets. I also found it more difficult to distinguish between steps, as they are closer together. Gene Smith's "Muddle" scales make sense to apply here. That means taking a MOS-like subset of a non-equal scale. For example, take the Miracle[10] MODMOS ssdLsssLss. We may group the steps (ss)(d)(Ls)(s)(sL)(s)(s). This mirrors the structure of the MOS scale of 10edo that goes 2 1 2 1 2 1 1. Since there are 7 different rotations of this MOS pattern, we may apply it in 7 different ways in our MODMOS. Here it is in steps of 72edo:
parent scale: 7 7 5 9 7 7 7 9 7 7
children:
form 2 1 2 1 2 1 1: 14 5 16 7 16 7 7
form 1 2 1 2 1 1 2: 7 12 9 14 7 9 14
form 2 1 2 1 1 2 1: 14 5 16 7 7 16 7
form 1 2 1 1 2 1 2: 7 12 9 7 14 9 14
form 2 1 1 2 1 2 1: 14 5 9 14 7 16 7
form 1 1 2 1 2 1 2: 7 7 14 7 14 9 14
It also works to take every other note, generating two different pentatonics with no tones in common.
So I did this same analysis with porcupine[7], and I used three different edos: 37edo, 22edo and 15edo:
| step | degrees of porcupine[7] in 37edo | cents value | degrees of porcupine[7] in 22edo | cents value | degrees of porcupine[7] in 15edo | cents value |
|---|---|---|---|---|---|---|
| * | * | * | * | * | * | * |
| c | 2 | 65 | 1 | 55 | 1 | 80 |
| * | * | * | * | * | * | * |
| d | 3 | 97 | 2 | 109 | 1 | 80 |
| s | 5 | 162 | 3 | 164 | 2 | 160 |
| L | 7 | 227 | 4 | 218 | 3 | 240 |
| A | 9 | 292 | 5 | 273 | 4 | 320 |
| * | * | * | * | * | * | * |
| dd | 6 | 195 | 4 | 218 | 2 | 160 |
| sd | 8 | 259 | 5 | 273 | 3 | 240 |
| ss=Ld | 10 | 324 | 6 | 327 | 4 | 320 |
| Ls=Ad | 12 | 389 | 7 | 382 | 5 | 400 |
| LL=As | 14 | 454 | 8 | 436 | 6 | 480 |
| AL | 16 | 519 | 9 | 491 | 7 | 560 |
| AA | 18 | 584 | 10 | 545 | 8 | 640 |
While 37edo porcupine distinguishes the full variety of 1-steps and 2-steps, 22edo and 15edo porcupine do not. 22edo has L=dd and A=sd. 15edo has s=dd, L=sd, and A=Ld. This suggests more chromatic/enharmonic nuance is available in 37edo porcupine, while more ambiguity and "puns" are available in 22edo and 15edo porcupine.
L/s ratio and consequences on MODMOS steps
Different L/s ratios produce different relationships between the steps of the above scales.
Case A: L/s<2. The chroma is smaller than the s step (c<s).
Case B: L/s=2, ie. L=2s. The chroma and the small step are the same (c=s).
Case C: L/s>2. The chroma is larger than the s step (c>s).
Case A1: 2<L/s<3/2. The diminished step (s-c) is smaller than the chroma (d<c).
Case A2: L/s=3/2. The diminished step and the chroma are the same (d=c).
Case A3: 3/2<L/s<1. The diminished step is larger than the chroma (d>c).
For Case B, there is no diminished step. Removing a chroma from an s step causes it to vanish. (d=0).
For Case C, assuming the diminished step is s-c, the diminished step is negative! Mike Battaglia, on FB, suggests we say that d is |s-c|. In this case, the diminished step is always smaller than the chroma. (d<c).
In all cases, A (L+c) is larger than s, c, or d.
In "An Approach to Chromatic/Enharmonic MODMOS scales" above, the first four examples satisfied Case A3, and so in each example A<L<s<d<c. A/L/s/d/c for each was: Sensi[8] in 46edo: 9/7/5/3/2; Miracle[10] in 72edo: 11/9/7/5/2; Porcupine[7] in 37edo: 9/7/5/3/2; Porcupine[7] in 22edo: 5/4/3/2/1. Notice the L/s ratio (bolded and underlined above) is between 1 and 3/2 in all cases. The exception is Porcupine[7] in 15edo, with L/s=3/2, and the A/L/s/d/c is 4/3/2/1/1. The 15edo example, which is Case A2 above, is the only one which doesn't distinguish all five of these primary steps.
My attraction to MODMOS scales in this range has to do with the fact that the smallest interval never appears melodically in a MODMOS, but only appears as the difference between some interval and one of its alterations. It seems to me this allows the greatest variety of potential MODMOS scales while assuring that no melodic steps appear that are "too small". Alternatively, it could mean that when the tiny chroma appears in a melody, it is signifying a change of mode. The limited range of L/s also assures that L and s are relatively close to the same size, and the original MOS and probably many of its MODMOSes has some of the very general melodic character of an edo.
Since we know the borders of this region to be L/s=1/1 and L/s=3/2, we know that the simplest L/s ratio with L and s whole numbers is (1+3)/(1+2)=4/3. This is merely a "freshman sum" -- the sum of the two numerators over the sum of the two denominators. We can expand this range by continuing to do freshman sums:
===> ===> ===> L and s closer to equal ===> ===> ===>
<=== <=== <=== c and d closer to equal <=== <=== <===
| 3/2 | 1/1 | |||||||||||||||
| 4/3 | ||||||||||||||||
| 7/5 | 5/4 | |||||||||||||||
| 10/7 | 11/8 | 9/7 | 6/5 | |||||||||||||
| 13/9 | 17/12 | 18/13 | 15/11 | 13/10 | 14/11 | 11/9 | 7/6 |
Notice that on each far end of the spectrum there is a different ambiguity. Moving toward L/s=1/1, L and s become closer to equal; moving toward L/s=3/2, c and d become closer to equal.
Expanding on "Maximal Evenness"
"Maximal Evenness" (ME, aka "Quasi-Equalness," QE) is a quality certain MOS scales within equal scales can have.
The maximally even scale will be one:
a. which contains exactly two step sizes as close in size as possible (differing by exactly one degree of the parent edo).
b. whose steps are distributed as evenly as possible.
For every n-edo, there are ME scales for every number of tones t where 1 < t < n.
In an ME scale, L and s differ by exactly one degree of the parent edo. So now I'm wondering about scales which differ by two degrees of the parent scale. I'm going to examine MOS Scales of 37edo to see if I can find scales of this type. I'll call it ME(2) for now, to mean something like, "Maximally Even, given that the difference between L and s must be 2 degrees". I was surprised to find ME(2) scales for every odd number of tones t where 1< t < 37 -- and none for any even numbers.
ME(2) for 3 tones: 13\37: 13 13 11
ME(2) for 5 tones: 7\37: 7 7 7 7 9
ME(2) for 7 tones: 5\37: 5 5 5 5 5 5 7
ME(2) for 9 tones: 8\37: 3 5 3 5 3 5 3 5 5
ME(2) for 11 tones: 17\37: 5 3 3 3 3 5 3 3 3 3 3
ME(2) for 13 tones: 3\37: 3 3 3 3 3 3 3 3 3 3 3 3 1
ME(2) for 15 tones: 10\37: 3 3 3 1 3 3 3 1 3 3 3 1 3 3 1
ME(2) for 17 tones: 11\37: 3 3 1 3 1 3 3 1 3 1 3 3 1 3 1 3 1
ME(2) for 19 tones: 4\37: 3 1 3 1 3 1 3 1 3 1 3 1 3 1 3 1 3 1 1
ME(2) for 21 tones: 14\37: 1 1 3 1 1 3 1 3 1 1 3 1 1 3 1 3 1 1 3 1 3
ME(2) for 23 tones: 16\37: 1 1 1 3 1 1 3 1 1 3 1 1 1 3 1 1 3 1 1 3 1 1 3
ME(2) for 25 tones: 6\37: 3 1 1 1 3 1 1 1 3 1 1 1 3 1 1 1 3 1 1 1 3 1 1 1 1
ME(2) for 27 tones: 15\37: 1 1 1 1 1 3 1 1 1 1 3 1 1 1 1 1 3 1 1 1 1 3 1 1 1 1 3
ME(2) for 29 tones: 9\37: 3 1 1 1 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 1 1 1
ME(2) for 31 tones: 12\37: 3 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1
ME(2) for 33 tones: 18\37 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
ME(2) for 35 tones: 1\37: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3
Ordinary ME scales eventually break down into L:s = 2:1 (not very "even" at all). Likewise, ME(2) scales eventually break down into L:s = 3:1, also not very even. But before 3:1 there's 5:3, before that 7:5, before that 9:7, etc. Interesting that there are no ME(2) scales with an even number of tones -- and interesting that in the ME(2) scales, all steps are odd numbers of degrees in size!
So now I'll look for ME(3) scales in 37edo. Although I'm generalizing the "Maximal Evenness" idea, it's quite clear that these scales are not necessarily "even" and that a better name is needed. I ain't got one yet.
It turns out that there are no ME(3) scales for numbers of tones that are divisible by 3! I also didn't see any for t = 20, 23, 26, 29, 32 or 35 -- and I have no idea why that would be!
ME(3) for 2 tones: 17\37: 17 20
ME(3) for 4 tones: 10\37: 10 10 10 7
ME(3) for 5 tones: 8\37: 8 8 8 8 5
ME(3) for 7 tones: 11\37: 7 4 7 4 7 4 4
ME(3) for 8 tones: 5\37: 5 5 5 5 5 5 5 2
ME(3) for 10 tones: 4\37: 4 4 4 4 4 4 4 4 4 1
ME(3) for 11 tones: 7\37: 5 2 5 2 5 2 5 2 5 2 2
ME(3) for 13 tones: 14\37: 1 4 1 4 4 1 4 1 4 4 1 4 4
ME(3) for 14 tones: 13\37: 2 2 2 2 5 2 2 2 2 5 2 2 2 5
ME(3) for 16 tones: 16\37: 1 1 4 1 4 1 4 1 1 4 1 4 1 4 1 4
ME(3) for 17 tones: 2\37: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 5
ME(3) for 19 tones: 6\37: 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 1
ME(3) for 20 tones: I don't see one!
ME(3) for 22 tones: 15\37: 1 1 1 1 4 1 1 1 4 1 1 1 1 4 1 1 1 4 1 1 1 4
ME(3) for 23 tones: I don't see one!
ME(3) for 25 tones: 9\37: 4 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 1 1 1
ME(3) for 26 tones: I don't see one!
ME(3) for 28 tones: 12\37: 4 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 1
ME(3) for 29 tones: I don't see one!
ME(3) for 31 tones: 18\37: 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
ME(3) for 32 tones: I don't see one!
ME(3) for 34 tones: 1\37: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4
ME(3) for 35 tones: I don't see one!
So that's where I'm leaving this problem for now.
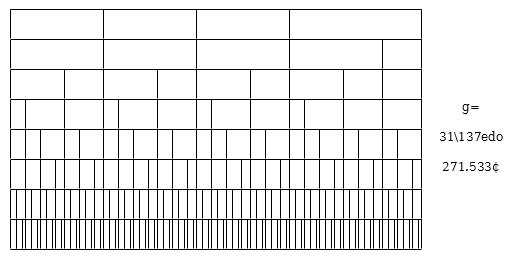
MOS Scales with similar generators
I'm wanting to do a study on the MOS generator spectrum with diagrams. I made two sample diagrams using 31\137edo and 32\137edo. Here they are right next to each other so I can compare and contrast.
Update: I decided to go with 127edo and have completed the visual study. See MOS Scales of 127edo.
Notes on Keenan Pepper's Diatonic-like MOS Scales
In the Xenharmonic Alliance Facebook Group, on Dec. 1, 2011, Keenan Pepper posted a short list of MOS scales, introducing them, 'The diatonic scale has both an extremely low average harmonic entropy, and also a very nearly maximum 'categorical channel capacity' (something I'm currently working on defining properly in terms of information theory - it basically means 'ability to tell different intervals and modes apart')."
This sounds interesting. I'm using this space to take some notes on the scales he lists:
| Scale Name | Generator | L | s | c | L:s | s:c |
|---|---|---|---|---|---|---|
| Porcupine[7] in 15edo | 160 | 240 | 160 | 80 | 2:1 = 2 | 2:1 = 2 |
| Porcupine[7] in 37edo | 162.16 | 227.03 | 162.16 | 64.87 | 7:5 = 1.4 | 5:2 = 2.5 |
| Porcupine[8] in 22edo | 163.64 | 212.18 | 163.64 | 54.55 | 4:3 = 1.33 | 3:1 = 3 |
| Neutral 3rds[7] in 17edo | 352.94 | 211.77 | 141.18 | 70.59 | 3:2 = 1.5 | 2:1 = 2 |
| Neutral 3rds[7] in 27edo | 355.56 | 222.22 | 133.33 | 88.89 | 5:3 = 1.67 | 3:2 = 1.5 |
| Sensi[8] in 19edo | 442.11 | 189.47 | 126.32 | 63.16 | 3:2 = 1.5 | 2:1 = 2 |
| Sensi[8] in 46edo | 443.48 | 182.61 | 130.44 | 52.17 | 7:5 = 1.4 | 5:2 = 2.5 |
| Sensi[8] in 27edo | 444.44 | 177.78 | 133.33 | 44.44 | 4:3 = 1.33 | 3:1 = 3 |
| Negri[9] in 19edo | 126.32 | 189.47 | 126.32 | 63.16 | 3:2 = 1.5 | 2:1 = 2 |
| Orwell[9] in 84edo | 271.43 | 157.14 | 114.29 | 42.86 | 11:8 = 1.38 | 8:3 = 2.67 |
| Orwell[9] in 53edo | 271.70 | 158.49 | 113.2 | 45.28 | 7:5 = 1.4 | 5:2 = 2.5 |
| Orwell[9] in 22edo | 272.73 | 163.64 | 109.09 | 54.55 | 3:2 = 1.5 | 2:1 = 2 |
| Orwell[9] in 35edo | 274.29 | 171.43 | 102.86 | 68.57 | 5:3 = 1.67 | 3:2 = 1.5 |
| Pajara[10] in 22edo | 109.09 | 163.64 | 109.09 | 54.55 | 3:2 = 1.5 | 2:1 = 2 |
| Blackwood[10] in 15edo | 80 | 160 | 80 | - | 2:1 = 2 |
Porcupine Temperament
I'm going to zoom in on Porcupine Temperament, which has been mentioned on the Facebook Xenharmonic Alliance page recently as a xenharmonic alternative to Meantone. Here's a little list of some of the things that were mentioned, so they can be collected in one place and not lost forever in the impenetrable Facebook Caverns:
- Keenan Pepper writes about how Porcupine tempers 27/20, 15/11 and 25/18 all to the 11/8 approximation, which, he claims, is a stronger consonance than any of the intervals mentioned.
- Mike Battaglia writes about how 81/80 is "tempered in" to 25/24, making it melodically useful instead of an "irritating mystery interval" which "introduces pitch drift".
- MB writes about Porcupine's MODMOS scales (which I will deal with more below), summarizing, "In short, when you're playing in porcupine, you should never feel like you're limited to just the 7 or 8-note MOS. Just freeform modify notes by L-s as much as you want, deliberately, in a willful attempt to explore porcupine chromaticism. It's even easier than meantone chromaticism."
- MB: "In porcupine, bIII/bIII/bIII = IV/IV. This is the same thing as saying that 6/5 * 6/5 * 6/5 = 4/3 * 4/3."
- Someone argues that Porcupine doesn't do that great in the 5-limit after all, saying, "Its only real selling-point over optimal meantone is simpler 7-limit and 11-limit approximations, but that assumes that these are a good in their own right and thus worth sacrificing some 5-limit efficiency; for anyone other than a dyed-in-the-wool xenharmonist, that's a questionable assumption to make." (As for me, I want those 7- and 11-limit approximations, and I could care less about a 5-limit temperament to rival meantone. I don't compose in 5-limit temperaments, period.)
- In response to the above, Keenan Pepper says, "You mentioned that almost every interval in the diatonic scale is a 9-limit consonance? Well, every interval in porcupine[7] is an 11-limit consonance! 1/1 10/9 9/8 6/5 5/4 4/3 11/8 16/11 3/2 8/5 5/3 16/9 9/5 2/1. Bam!" (This is relevant to my work, which assumes composers want 11-limit approximations.)
- I (Andrew Heathwaite) added, "...maybe another description for what Porcupine is good for is a *gateway* from 5 and 7 to 11, for those comfortable with the former and curious about the latter. As a full 11-limit temperament, it is efficient and easy."
Porcupine Chromaticism
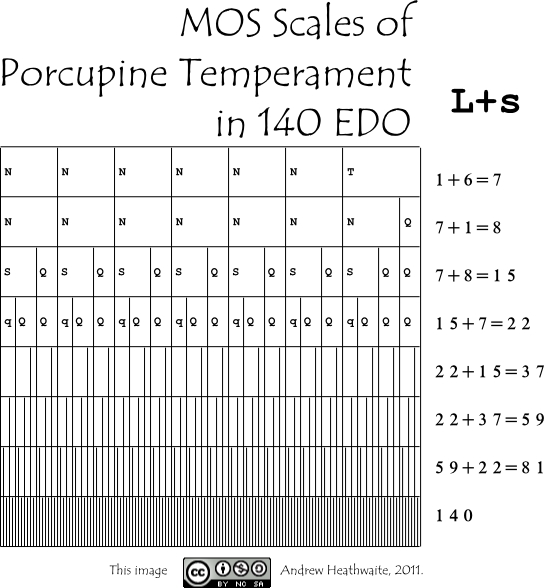
Mike Battaglia has brought up this idea of Porcupine Chromaticism and given MODMOS Scales of Porcupine as specific examples. So to start that exploration, I've made a diagram of all the MOS scales that Porcupine makes possible, starting at Porcupine[7], and terminating at 140edo, which is arguably an optimal tuning for Porcupine. Take a look:
On the XA Facebook page, Paul Erlich showed me some horograms in which the two intervals I call Q and q (for greater and lesser quartertone) switch places, leading me to conclude that there is no standard form for Porcupine[22]. This means that, after a certain point, we have to pick a tuning (pick a side of 22edo for the generator to land on) if we want to explore Porcupine chromaticism that deeply into it, i.e. that far down the generator chain.
Modes of Porcupine[7]
The following modes are given in steps of 22edo. They are rotations of one moment of symmetry scale with two step sizes: a neutral tone (3\22) and a large whole tone (4\22). On the right is a contiguous chain of 7 tones separated by 6 iterations of the Porcupine generator. Modes in bold have a 3/2 approximation above the bass -- this can be verified easily by looking at the chain. The perfect fifth approximation is -3g, so every mode with a "-3" in the chain has a perfect fifth over the bass.
3 3 3 3 3 3 4 .. 0 1 2 3 4 5 6
3 3 3 3 3 4 3 .. -1 0 1 2 3 4 5
3 3 3 3 4 3 3 .. -2 -1 0 1 2 3 4
3 3 3 4 3 3 3 .. -3 -2 -1 0 1 2 3
3 3 4 3 3 3 3 .. -4 -3 -2 -1 0 1 2
3 4 3 3 3 3 3 .. -5 -4 -3 -2 -1 0 1
4 3 3 3 3 3 3 .. -6 -5 -4 -3 -2 -1 0
Modes of Porcupine[7] that have one chromatic alteration
The following list includes all the modes (hopefully) that can be generated by shifting one tone of Porcupine[7] by one quartertone interval (chroma), which is one degree in 22edo. This produces scales with three step sizes -- in addition to a neutral tone (3\22) and large whole tone (4\22) there is now a semitone as well (2\22). In addition, two scales (and their rotations of course) have a 5-step subminor third. Underscores represent gaps in the chain of Porcupine generators. Note that lowering a tone by one quartertone interval (chroma) means sending it forward 7 spaces in the chain of generators, while raising a tone by one chroma means sending it backward 7 spaces in the chain of generators. This is how we wind up with such large gaps in the chain. Again, modes with perfect fifths from the bass are bolded.
2 4 3 3 3 3 4 .. 0 _ 2 3 4 5 6 _ 8
4 3 3 3 3 4 2 .. -8 _ -6 -5 -4 -3 -2 _ 0 === Mike Battaglia's Porcupine[7] 6|0 #7
3 3 3 3 4 2 4 .. -2 _ 0 1 2 3 4 _ 6
3 3 3 4 2 4 3 .. -3 _ -1 0 1 2 3 _ 5
3 3 4 2 4 3 3 .. -4 _ -2 -1 0 1 2 _ 4
3 4 2 4 3 3 3 .. -5 _ -3 -2 -1 0 1 _ 3
4 2 4 3 3 3 3 .. -6 _ -4 -3 -2 -1 0 _ 2
2 3 4 3 3 3 4 .. 0 _ _ 3 4 5 6 _ 8 9
3 4 3 3 3 4 2 .. -8 _ _ -5 -4 -3 -2 _ 0 1
4 3 3 3 4 2 3 .. -9 _ _ -6 -5 -4 -3 _ -1 0
3 3 3 4 2 3 4 .. -3 _ _ 0 1 2 3 _ 5 6
3 3 4 2 3 4 3 .. -4 _ _ -1 0 1 2 _ 4 5
3 4 2 3 4 3 3 .. -5 _ _ -2 -1 0 1 _ 3 4
4 2 3 4 3 3 3 .. -6 _ _ -3 -2 -1 0 _ 1 2 === Mike Battaglia's Porcupine[7] 3|3 #2
2 4 3 3 3 4 3 .. -1 0 _ 2 3 4 5 _ _ 8
4 3 3 3 4 3 2 .. -9 -8 _ -6 -5 -4 -3 _ _ 0
3 3 3 4 3 2 4 .. -3 -2 _ 0 1 2 3 _ _ 6
3 3 4 3 2 4 3 .. -4 -3 _ -1 0 1 2 _ _ 5 === one of Andrew's faves
3 4 3 2 4 3 3 .. -5 -4 _ -2 -1 0 1 _ _ 4
4 3 2 4 3 3 3 .. -6 -5 _ -3 -2 -1 0 _ _ 3 === Mike Battaglia's Porcupine[7] 6|0 b4
3 2 4 3 3 3 4 .. 0 1 _ 3 4 5 6 _ _ 9
2 3 3 4 3 3 4 .. 0 _ _ _ 4 5 6 _ 8 9 10
3 3 4 3 3 4 2 .. -8 _ _ _ -4 -3 -2 _ 0 1 2
3 4 3 3 4 2 3 .. -9 _ _ _ -5 -4 -3 _ -1 0 1
4 3 3 4 2 3 3 .. -10 _ _ _ -6 -5 -4 _ -2 -1 0
3 3 4 2 3 3 4 .. -4 _ _ _ 0 1 2 _ 4 5 6
3 4 2 3 3 4 3 .. -5 _ _ _ -1 0 1 _ 3 4 5
4 2 3 3 4 3 3 .. -6 _ _ _ -2 -1 0 _ 2 3 4
2 4 3 3 4 3 3 .. -2 -1 0 _ 2 3 4 _ _ _ 8
4 3 3 4 3 3 2 .. -10 -9 -8 _ -6 -5 -4 _ _ _ 0
3 3 4 3 3 2 4 .. -4 -3 -2 _ 0 1 2 _ _ _ 6
3 4 3 3 2 4 3 .. -5 -4 -3 _ -1 0 1 _ _ _ 5
4 3 3 2 4 3 3 .. -6 -5 -4 _ -2 -1 0 _ _ _ 4
3 3 2 4 3 3 4 .. 0 1 2 _ 4 5 6 _ _ _ 10
3 2 4 3 3 4 3 .. -1 0 1 _ 3 4 5 _ _ _ 9
2 3 3 3 4 3 4 .. 0 _ _ _ _ 5 6 _ 8 9 10 11
3 3 3 4 3 4 2 .. -8 _ _ _ _ -3 -2 _ 0 1 2 3
3 3 4 3 4 2 3 .. -9 _ _ _ _ -4 -3 _ -1 0 1 2
3 4 3 4 2 3 3 .. -10 _ _ _ _ -5 -4 _ -2 -1 0 1
4 3 4 2 3 3 3 .. -11 _ _ _ _ -6 -5 _ -3 -2 -1 0
3 4 2 3 3 3 4 .. -5 _ _ _ _ 0 1 _ 3 4 5 6
4 2 3 3 3 4 3 .. -6 _ _ _ _ -1 0 _ 2 3 4 5
2 4 3 4 3 3 3 .. -3 -2 -1 0 _ 2 3 _ _ _ _ 8
4 3 4 3 3 3 2 .. -11 -10 -9 -8 _ -6 -5 _ _ _ _ 0
3 4 3 3 3 2 4 .. -5 -4 -3 -2 _ 0 1 _ _ _ _ 6 === one of Andrew's faves
4 3 3 3 2 4 3 .. -6 -5 -4 -3 _ -1 0 _ _ _ _ 5
3 3 3 2 4 3 4 .. 0 1 2 3 _ 5 6 _ _ _ _ 11
3 3 2 4 3 4 3 .. -1 0 1 2 _ 4 5 _ _ _ _ 10
3 2 4 3 4 3 3 .. -2 -1 0 1 _ 3 4 _ _ _ _ 9
2 3 3 3 3 4 4 .. 0 _ _ _ _ _ 6 _ 8 9 10 11 12
3 3 3 3 4 4 2 .. -8 _ _ _ _ _ -2 _ 0 1 2 3 4
3 3 3 4 4 2 3 .. -9 _ _ _ _ _ -3 _ -1 0 1 2 3
3 3 4 4 2 3 3 .. -10 _ _ _ _ _ -4 _ -2 -1 0 1 2
3 4 4 2 3 3 3 .. -11 _ _ _ _ _ -5 _ -3 -2 -1 0 1
4 4 2 3 3 3 3 .. -12 _ _ _ _ _ -6 _ -4 -3 -2 -1 0
4 2 3 3 3 3 4 .. -6 _ _ _ _ _ 0 _ 2 3 4 5 6
2 4 4 3 3 3 3 .. -4 -3 -2 -1 0 _ 2 _ _ _ _ _ 8
4 4 3 3 3 3 2 .. -12 -11 -10 -9 -8 _ -6 _ _ _ _ _ 0
4 3 3 3 3 2 4 .. -6 -5 -4 -3 -2 _ 0 _ _ _ _ _ 6 === Mike Battaglia's Porcupine[7] 6|0 b7
3 3 3 3 2 4 4 .. 0 1 2 3 4 _ 6 _ _ _ _ _ 12
3 3 3 2 4 4 3 .. -1 0 1 2 3 _ 5 _ _ _ _ _ 11
3 3 2 4 4 3 3 .. -2 -1 0 1 2 _ 4 _ _ _ _ _ 10
3 2 4 4 3 3 3 .. -3 -2 -1 0 1 _ 3 _ _ _ _ _ 9
2 3 3 3 3 3 5 .. 0 _ _ _ _ _ _ _ 8 9 10 11 12 13
3 3 3 3 3 5 2 .. -8 _ _ _ _ _ _ _ 0 1 2 3 4 5
3 3 3 3 5 2 3 .. -9 _ _ _ _ _ _ _ -1 0 1 2 3 4
3 3 3 5 2 3 3 .. -10 _ _ _ _ _ _ _ -2 -1 0 1 2 3
3 3 5 2 3 3 3 .. -11 _ _ _ _ _ _ _ -3 -2 -1 0 1 2
3 5 2 3 3 3 3 .. -12 _ _ _ _ _ _ _ -4 -3 -2 -1 0 1
5 2 3 3 3 3 3 .. -13 _ _ _ _ _ _ _ -5 -4 -3 -2 -1 0
2 5 3 3 3 3 3 .. -5 -4 -3 -2 -1 0 _ _ _ _ _ _ _ 8
5 3 3 3 3 3 2 .. -13 -12 -11 -10 -9 -8 _ _ _ _ _ _ _ 0
3 3 3 3 3 2 5 .. 0 1 2 3 4 5 _ _ _ _ _ _ _ 13
3 3 3 3 2 5 3 .. -1 0 1 2 3 4 _ _ _ _ _ _ _ 12
3 3 3 2 5 3 3 .. -2 -1 0 1 2 3 _ _ _ _ _ _ _ 11
3 3 2 5 3 3 3 .. -3 -2 -1 0 1 2 _ _ _ _ _ _ _ 10
3 2 5 3 3 3 3 .. -4 -3 -2 -1 0 1 _ _ _ _ _ _ _ 9
Update: Mike Battaglia has made a dedicated page for explaining these modes -- yay! -- see Porcupine Temperament Modal Harmony.
Orwell[9], meet Porcupine[7]
I've done a little composing in Orwell[9], which, in 22edo, goes 3 2 3 2 3 2 3 2 2 (where L=3\22 and s=2\22), so I want to apply MODMOS to that. To make a MODMOS here, we alter a tone by a single degree of 22edo, same as we do in Porcupine[7]. This is our "chroma," and it's generated by taking L-s: so in 22edo we have 3\22-2\22=1\22. We wind up with either:
- A permutation of the four large and five small steps, eg. 3 3 2 2 3 2 3 2 2
- How many of these are there? Does anyone know a formula for finding the number of possible permutations when some of the items are interchangable? Here the question is, how many permutations can we make of 4 items of Type A and 5 items of Type B?
- A scale with three step sizes: large, small, and smaller, eg. 3 2 3 2 3 2 3 3 1
- In 22edo, our "smaller" step is the same as our "chroma" (which is the interval that we alter a tone by to produce a MODMOS, L-s). However, this is not the case in larger edos! Look at 31edo, where our initial scale is 4 3 4 3 4 3 4 3 3. Now our chroma is 4\31-3\31=1\31 and our "smaller" step is 2\31: 4 3 4 3 4 3 4 4 2! We get our "smaller" step by starting with s (3\31) and taking away a chroma (1\31), so we have 3\31-1\31=2\31.
- So what should we call the "smaller" interval in our scale? Maybe some kind of diminished something-or-another?
- A scale with four steps sizes: large, small, larger and smaller, eg. 4 1 3 2 3 2 3 2 2
- This is generated by starting with L and adding a chroma, so in 22edo it's 3\22+1\22=4\22. In 31edo, that would be 4\31+1\31=5\31, and the scale in question would be 5 2 4 3 4 3 4 3 3.
- So what should we call the "larger" step? Some kind of augmented something-or-another?
- Note that in 22edo, our "larger" step, 4\22, is the same as two of our small steps (2\22+2\22=4\22), even though we generated our "larger" step by adding a chroma to a large step (3\22+1\22). In 31edo, our "larger" step is NOT the same as two of our small steps (4\31+1\31=5\31 does not equal 3\31+3\31=6\31)!
So we can take advantage of the fact that two small steps in 22edo's Orwell[9] (2\22) make one "larger" step (4\22). If 9 tones is a few too many, we can turn some 2+2's into 4's. So for instance, the first example above goes:
3 3 2 2 3 2 3 2 2
3 3 4 3 2 3 4.
But check it out! 3 3 4 3 2 3 4 is a MODMOS of Porcupine[7]! Here's how we can get it by chromatically-altering Porcupine[7] one tone at a time:
3 3 3 3 3 3 4
3 3 4 2 3 3 4
3 3 4 3 2 3 4
And we see, not surprisingly, that this doesn't work the same way in 31edo.
Start with a MODMOS of Orwell[9]: 4 4 3 3 4 3 4 3 3
Combine small steps: 4 4 6 4 3 4 6
4 4 4 4 4 4 7 is as close as we can get to Porcupine[7], and it sure ain't the same. Our chroma (L-s) is 3\31, really different!
4 4 7 1 4 4 7
4 4 7 1 4 1 7
Not even close!
Names for steps
This is getting silly! We need better names.....
So, as proposed on the page for MODMOS Scales, we could call L-s a "chroma" and abbreviate it "c". That's a good start.
We have another step that's s-c, or s-(L-s) = s-L+s = 2s-L. In Porcupine[7] in 22edo, that's:
s-c = 3\22-1\22 = 2\22
or
2s-L = 2(3\22)-4\22 = 6\22-4\22 = 2\22.
Some kind of diminished step?
And we have another step that's L+c, or L+(L-s) = 2L-s. In Porcupine[7] in 22edo, that's:
L+c = 4\22+1\22 = 5\22
or
2L-s = 2(4\22)-3\22 = 8\22-3\22 = 5\22.
Some kind of augmented step?
Mike Battaglia proposes (at least in the case of Porcupine) "d" for s-c and "A" for L+c....
So I posted to XA: "Ok, thinking it over, A and d are interesting choices to describe the additional steps, since they're so general. "d" is the small step minus one chroma, or s-c. But since the chroma itself is L-s, we can define d directly in terms of L and s as 2s-L. Meanwhile, "A" is the large step plus one chroma, or L+c. Described in terms of L and s, "A" is 2L-s. This allows us to quickly compute c, A, and d quickly, given L and s. As one example, Orwell[9] in 53edo has L=7 and s=5. So c=L-s=7-5=2; d=2s-L=2(5)-7=3; and A=2L-s=2(7)-5=9. Sure enough, a MODMOS of Orwell[9] with all four of these steps can be easily generated. Start with 7 5 7 5 7 5 7 5 5 and shift the second tone up by one chroma (which we computed to be 2\53), producing 9 3 7 5 7 5 7 5 5, which generalizes to AdLsLsLss! (Note that in 53edo Orwell[9] 2s=10 and A=9, not equal; while in 22edo's version of Orwell[9] 2s=4 and A=4, a potential 22edo Orwell pun.) ... (Oh, and another pun is possible here, since c and d are both 1 degree in 22edo but 2 and 3 degrees, respectively, in 53edo.)"
![map_of_sensi[8].png](/images/a/a6/Map_of_sensi-8-.png)
![map_of_sensi[11]_correction2.png](/images/9/97/Map_of_sensi-11-_correction2.png)