List of MOS scales in 31edo

From Xenharmonic Wiki
(Redirected from 31edo MOS scales)
Jump to navigation Jump to search

This page lists all moment of symmetry scales in 31edo.

Single-period MOS scales

Generators 16\31 and 15\31
Step visualization MOS (name) Step sizes Step ratio
├───────────────┼──────────────┤ 1L 1s 16, 15 16:15
├┼──────────────┼──────────────┤ 2L 1s 15, 1 15:1
├┼┼─────────────┼┼─────────────┤ 2L 3s 14, 1 14:1
├┼┼┼────────────┼┼┼────────────┤ 2L 5s (antidiatonic) 13, 1 13:1
├┼┼┼┼───────────┼┼┼┼───────────┤ 2L 7s (balzano) 12, 1 12:1
├┼┼┼┼┼──────────┼┼┼┼┼──────────┤ 2L 9s 11, 1 11:1
├┼┼┼┼┼┼─────────┼┼┼┼┼┼─────────┤ 2L 11s 10, 1 10:1
├┼┼┼┼┼┼┼────────┼┼┼┼┼┼┼────────┤ 2L 13s 9, 1 9:1
├┼┼┼┼┼┼┼┼───────┼┼┼┼┼┼┼┼───────┤ 2L 15s 8, 1 8:1
├┼┼┼┼┼┼┼┼┼──────┼┼┼┼┼┼┼┼┼──────┤ 2L 17s 7, 1 7:1
├┼┼┼┼┼┼┼┼┼┼─────┼┼┼┼┼┼┼┼┼┼─────┤ 2L 19s 6, 1 6:1
├┼┼┼┼┼┼┼┼┼┼┼────┼┼┼┼┼┼┼┼┼┼┼────┤ 2L 21s 5, 1 5:1
├┼┼┼┼┼┼┼┼┼┼┼┼───┼┼┼┼┼┼┼┼┼┼┼┼───┤ 2L 23s 4, 1 4:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼┼┼┼┼┼──┤ 2L 25s 3, 1 3:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼┼┼┼┼┼─┤ 2L 27s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 17\31 and 14\31
Step visualization MOS (name) Step sizes Step ratio
├────────────────┼─────────────┤ 1L 1s 17, 14 17:14
├──┼─────────────┼─────────────┤ 2L 1s 14, 3 14:3
├──┼──┼──────────┼──┼──────────┤ 2L 3s 11, 3 11:3
├──┼──┼──┼───────┼──┼──┼───────┤ 2L 5s (antidiatonic) 8, 3 8:3
├──┼──┼──┼──┼────┼──┼──┼──┼────┤ 2L 7s (balzano) 5, 3 5:3
├──┼──┼──┼──┼──┼─┼──┼──┼──┼──┼─┤ 9L 2s 3, 2 3:2
├┼─┼┼─┼┼─┼┼─┼┼─┼─┼┼─┼┼─┼┼─┼┼─┼─┤ 11L 9s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 18\31 and 13\31
Step visualization MOS (name) Step sizes Step ratio
├─────────────────┼────────────┤ 1L 1s 18, 13 18:13
├────┼────────────┼────────────┤ 2L 1s 13, 5 13:5
├────┼────┼───────┼────┼───────┤ 2L 3s 8, 5 8:5
├────┼────┼────┼──┼────┼────┼──┤ 5L 2s (diatonic) 5, 3 5:3
├─┼──┼─┼──┼─┼──┼──┼─┼──┼─┼──┼──┤ 7L 5s 3, 2 3:2
├─┼─┼┼─┼─┼┼─┼─┼┼─┼┼─┼─┼┼─┼─┼┼─┼┤ 12L 7s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 19\31 and 12\31
Step visualization MOS (name) Step sizes Step ratio
├──────────────────┼───────────┤ 1L 1s 19, 12 19:12
├──────┼───────────┼───────────┤ 2L 1s 12, 7 12:7
├──────┼──────┼────┼──────┼────┤ 3L 2s 7, 5 7:5
├─┼────┼─┼────┼────┼─┼────┼────┤ 5L 3s (oneirotonic) 5, 2 5:2
├─┼─┼──┼─┼─┼──┼─┼──┼─┼─┼──┼─┼──┤ 5L 8s 3, 2 3:2
├─┼─┼─┼┼─┼─┼─┼┼─┼─┼┼─┼─┼─┼┼─┼─┼┤ 13L 5s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 20\31 and 11\31
Step visualization MOS (name) Step sizes Step ratio
├───────────────────┼──────────┤ 1L 1s 20, 11 20:11
├────────┼──────────┼──────────┤ 2L 1s 11, 9 11:9
├────────┼────────┼─┼────────┼─┤ 3L 2s 9, 2 9:2
├──────┼─┼──────┼─┼─┼──────┼─┼─┤ 3L 5s (checkertonic) 7, 2 7:2
├────┼─┼─┼────┼─┼─┼─┼────┼─┼─┼─┤ 3L 8s 5, 2 5:2
├──┼─┼─┼─┼──┼─┼─┼─┼─┼──┼─┼─┼─┼─┤ 3L 11s 3, 2 3:2
├┼─┼─┼─┼─┼┼─┼─┼─┼─┼─┼┼─┼─┼─┼─┼─┤ 14L 3s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 21\31 and 10\31
Step visualization MOS (name) Step sizes Step ratio
├────────────────────┼─────────┤ 1L 1s 21, 10 21:10
├──────────┼─────────┼─────────┤ 1L 2s 11, 10 11:10
├┼─────────┼─────────┼─────────┤ 3L 1s 10, 1 10:1
├┼┼────────┼┼────────┼┼────────┤ 3L 4s (mosh) 9, 1 9:1
├┼┼┼───────┼┼┼───────┼┼┼───────┤ 3L 7s (sephiroid) 8, 1 8:1
├┼┼┼┼──────┼┼┼┼──────┼┼┼┼──────┤ 3L 10s 7, 1 7:1
├┼┼┼┼┼─────┼┼┼┼┼─────┼┼┼┼┼─────┤ 3L 13s 6, 1 6:1
├┼┼┼┼┼┼────┼┼┼┼┼┼────┼┼┼┼┼┼────┤ 3L 16s 5, 1 5:1
├┼┼┼┼┼┼┼───┼┼┼┼┼┼┼───┼┼┼┼┼┼┼───┤ 3L 19s 4, 1 4:1
├┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼──┼┼┼┼┼┼┼┼──┤ 3L 22s 3, 1 3:1
├┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼─┼┼┼┼┼┼┼┼┼─┤ 3L 25s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 22\31 and 9\31
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────┼────────┤ 1L 1s 22, 9 22:9
├────────────┼────────┼────────┤ 1L 2s 13, 9 13:9
├───┼────────┼────────┼────────┤ 3L 1s 9, 4 9:4
├───┼───┼────┼───┼────┼───┼────┤ 3L 4s (mosh) 5, 4 5:4
├───┼───┼───┼┼───┼───┼┼───┼───┼┤ 7L 3s (dicoid) 4, 1 4:1
├──┼┼──┼┼──┼┼┼──┼┼──┼┼┼──┼┼──┼┼┤ 7L 10s 3, 1 3:1
├─┼┼┼─┼┼┼─┼┼┼┼─┼┼┼─┼┼┼┼─┼┼┼─┼┼┼┤ 7L 17s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 23\31 and 8\31
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────┼───────┤ 1L 1s 23, 8 23:8
├──────────────┼───────┼───────┤ 1L 2s 15, 8 15:8
├──────┼───────┼───────┼───────┤ 3L 1s 8, 7 8:7
├──────┼──────┼┼──────┼┼──────┼┤ 4L 3s (smitonic) 7, 1 7:1
├─────┼┼─────┼┼┼─────┼┼┼─────┼┼┤ 4L 7s 6, 1 6:1
├────┼┼┼────┼┼┼┼────┼┼┼┼────┼┼┼┤ 4L 11s 5, 1 5:1
├───┼┼┼┼───┼┼┼┼┼───┼┼┼┼┼───┼┼┼┼┤ 4L 15s 4, 1 4:1
├──┼┼┼┼┼──┼┼┼┼┼┼──┼┼┼┼┼┼──┼┼┼┼┼┤ 4L 19s 3, 1 3:1
├─┼┼┼┼┼┼─┼┼┼┼┼┼┼─┼┼┼┼┼┼┼─┼┼┼┼┼┼┤ 4L 23s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 24\31 and 7\31
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────┼──────┤ 1L 1s 24, 7 24:7
├────────────────┼──────┼──────┤ 1L 2s 17, 7 17:7
├─────────┼──────┼──────┼──────┤ 1L 3s 10, 7 10:7
├──┼──────┼──────┼──────┼──────┤ 4L 1s 7, 3 7:3
├──┼──┼───┼──┼───┼──┼───┼──┼───┤ 4L 5s (gramitonic) 4, 3 4:3
├──┼──┼──┼┼──┼──┼┼──┼──┼┼──┼──┼┤ 9L 4s 3, 1 3:1
├─┼┼─┼┼─┼┼┼─┼┼─┼┼┼─┼┼─┼┼┼─┼┼─┼┼┤ 9L 13s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 25\31 and 6\31
Step visualization MOS (name) Step sizes Step ratio
├────────────────────────┼─────┤ 1L 1s 25, 6 25:6
├──────────────────┼─────┼─────┤ 1L 2s 19, 6 19:6
├────────────┼─────┼─────┼─────┤ 1L 3s 13, 6 13:6
├──────┼─────┼─────┼─────┼─────┤ 1L 4s 7, 6 7:6
├┼─────┼─────┼─────┼─────┼─────┤ 5L 1s (machinoid) 6, 1 6:1
├┼┼────┼┼────┼┼────┼┼────┼┼────┤ 5L 6s 5, 1 5:1
├┼┼┼───┼┼┼───┼┼┼───┼┼┼───┼┼┼───┤ 5L 11s 4, 1 4:1
├┼┼┼┼──┼┼┼┼──┼┼┼┼──┼┼┼┼──┼┼┼┼──┤ 5L 16s 3, 1 3:1
├┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┼┼┼┼┼─┤ 5L 21s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 26\31 and 5\31
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────────┼────┤ 1L 1s 26, 5 26:5
├────────────────────┼────┼────┤ 1L 2s 21, 5 21:5
├───────────────┼────┼────┼────┤ 1L 3s 16, 5 16:5
├──────────┼────┼────┼────┼────┤ 1L 4s 11, 5 11:5
├─────┼────┼────┼────┼────┼────┤ 1L 5s (antimachinoid) 6, 5 6:5
├┼────┼────┼────┼────┼────┼────┤ 6L 1s (archaeotonic) 5, 1 5:1
├┼┼───┼┼───┼┼───┼┼───┼┼───┼┼───┤ 6L 7s 4, 1 4:1
├┼┼┼──┼┼┼──┼┼┼──┼┼┼──┼┼┼──┼┼┼──┤ 6L 13s 3, 1 3:1
├┼┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼┼─┼┼┼┼─┤ 6L 19s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 27\31 and 4\31
Step visualization MOS (name) Step sizes Step ratio
├──────────────────────────┼───┤ 1L 1s 27, 4 27:4
├──────────────────────┼───┼───┤ 1L 2s 23, 4 23:4
├──────────────────┼───┼───┼───┤ 1L 3s 19, 4 19:4
├──────────────┼───┼───┼───┼───┤ 1L 4s 15, 4 15:4
├──────────┼───┼───┼───┼───┼───┤ 1L 5s (antimachinoid) 11, 4 11:4
├──────┼───┼───┼───┼───┼───┼───┤ 1L 6s (onyx) 7, 4 7:4
├──┼───┼───┼───┼───┼───┼───┼───┤ 7L 1s (pine) 4, 3 4:3
├──┼──┼┼──┼┼──┼┼──┼┼──┼┼──┼┼──┼┤ 8L 7s 3, 1 3:1
├─┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┼─┼┼┤ 8L 15s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 28\31 and 3\31
Step visualization MOS (name) Step sizes Step ratio
├───────────────────────────┼──┤ 1L 1s 28, 3 28:3
├────────────────────────┼──┼──┤ 1L 2s 25, 3 25:3
├─────────────────────┼──┼──┼──┤ 1L 3s 22, 3 22:3
├──────────────────┼──┼──┼──┼──┤ 1L 4s 19, 3 19:3
├───────────────┼──┼──┼──┼──┼──┤ 1L 5s (antimachinoid) 16, 3 16:3
├────────────┼──┼──┼──┼──┼──┼──┤ 1L 6s (onyx) 13, 3 13:3
├─────────┼──┼──┼──┼──┼──┼──┼──┤ 1L 7s (antipine) 10, 3 10:3
├──────┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 8s (antisubneutralic) 7, 3 7:3
├───┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 1L 9s (antisinatonic) 4, 3 4:3
├┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┤ 10L 1s 3, 1 3:1
├┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┼┼─┤ 10L 11s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 29\31 and 2\31
Step visualization MOS (name) Step sizes Step ratio
├────────────────────────────┼─┤ 1L 1s 29, 2 29:2
├──────────────────────────┼─┼─┤ 1L 2s 27, 2 27:2
├────────────────────────┼─┼─┼─┤ 1L 3s 25, 2 25:2
├──────────────────────┼─┼─┼─┼─┤ 1L 4s 23, 2 23:2
├────────────────────┼─┼─┼─┼─┼─┤ 1L 5s (antimachinoid) 21, 2 21:2
├──────────────────┼─┼─┼─┼─┼─┼─┤ 1L 6s (onyx) 19, 2 19:2
├────────────────┼─┼─┼─┼─┼─┼─┼─┤ 1L 7s (antipine) 17, 2 17:2
├──────────────┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 8s (antisubneutralic) 15, 2 15:2
├────────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 9s (antisinatonic) 13, 2 13:2
├──────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 10s 11, 2 11:2
├────────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 11s 9, 2 9:2
├──────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 12s 7, 2 7:2
├────┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 13s 5, 2 5:2
├──┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 1L 14s 3, 2 3:2
├┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┤ 15L 1s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1
Generators 30\31 and 1\31
Step visualization MOS (name) Step sizes Step ratio
├─────────────────────────────┼┤ 1L 1s 30, 1 30:1
├────────────────────────────┼┼┤ 1L 2s 29, 1 29:1
├───────────────────────────┼┼┼┤ 1L 3s 28, 1 28:1
├──────────────────────────┼┼┼┼┤ 1L 4s 27, 1 27:1
├─────────────────────────┼┼┼┼┼┤ 1L 5s (antimachinoid) 26, 1 26:1
├────────────────────────┼┼┼┼┼┼┤ 1L 6s (onyx) 25, 1 25:1
├───────────────────────┼┼┼┼┼┼┼┤ 1L 7s (antipine) 24, 1 24:1
├──────────────────────┼┼┼┼┼┼┼┼┤ 1L 8s (antisubneutralic) 23, 1 23:1
├─────────────────────┼┼┼┼┼┼┼┼┼┤ 1L 9s (antisinatonic) 22, 1 22:1
├────────────────────┼┼┼┼┼┼┼┼┼┼┤ 1L 10s 21, 1 21:1
├───────────────────┼┼┼┼┼┼┼┼┼┼┼┤ 1L 11s 20, 1 20:1
├──────────────────┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 12s 19, 1 19:1
├─────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 13s 18, 1 18:1
├────────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 14s 17, 1 17:1
├───────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 15s 16, 1 16:1
├──────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 16s 15, 1 15:1
├─────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 17s 14, 1 14:1
├────────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 18s 13, 1 13:1
├───────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 19s 12, 1 12:1
├──────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 20s 11, 1 11:1
├─────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 21s 10, 1 10:1
├────────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 22s 9, 1 9:1
├───────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 23s 8, 1 8:1
├──────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 24s 7, 1 7:1
├─────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 25s 6, 1 6:1
├────┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 26s 5, 1 5:1
├───┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 27s 4, 1 4:1
├──┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 28s 3, 1 3:1
├─┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 1L 29s 2, 1 2:1
├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤ 31edo 1, 1 1:1

Pergen Names

Temperaments supported by 31edo may also be referred by pergen names.

  • 1\31 = (P8, P4/13)
  • 2\31 = (P8, P5/9)
  • 3\31 = (P8, P5/6)
  • 4\31 = (P8, P11/11)
  • 5\31 = (P8, ccP4/15)
  • 6\31 = (P8, P5/3)
  • 7\31 = (P8, P12/7)
  • 8\31 = (P8, ccP5/10)
  • 9\31 = (P8, P5/2)
  • 10\31 = (P8, ccP5/8)
  • 11\31 = (P8, P11/4)
  • 12\31 = (P8, c⁵P4/14)
  • 13\31 = (P8, P5)
  • 14\31 = (P8, c⁵P4/12)
  • 15\31 = (P8, ccP4/5)

Gallery

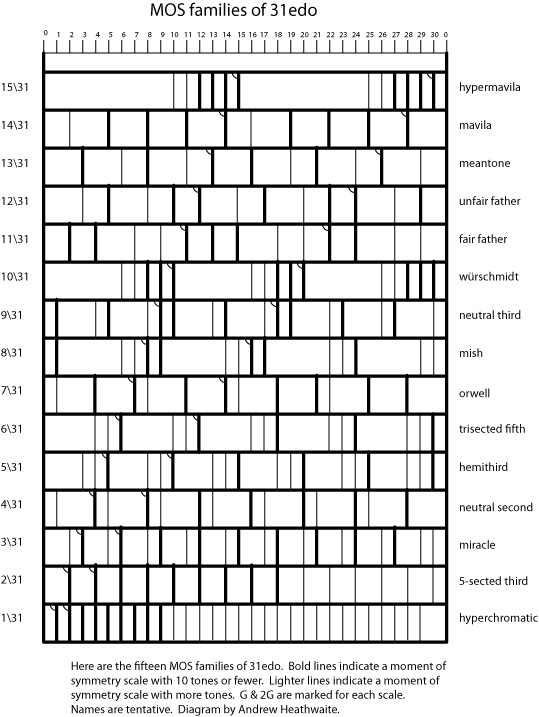31edo_mos_families.jpg
MOS families of 31edo, with selected MOS scales for each generator.
Retrieved from "https://en.xen.wiki/index.php?title=List_of_MOS_scales_in_31edo&oldid=129288"