User:Lucius Chiaraviglio/Keyboard Layout Lab/Various rank-3 temperament Lumatone mappings

From Xenharmonic Wiki
< User:Lucius Chiaraviglio | Keyboard Layout Lab
Revision as of 08:02, 2 July 2025 by Lucius Chiaraviglio (talk | contribs) (→76edo (2 mappings demonstrated to work): Finish up the temperament text for the 7:5 step ratio version)
Jump to navigation Jump to search

Due to the Lumatone wizardry of Bryan Deister, including at the larger EDO sizes, rank-3 temperament lumatone mappings are going here to avoid having other Keyboard Layout Lab pages getting too many Lumatone mappings (which causes the dreaded "template include too large" error).

Moved named rank-3 temperament Lumatone mappings here from Keyboard Layout Lab: Lucius Chiaraviglio (talk) 05:52, 21 June 2025 (UTC) Moved unnamed rank-3 temperament Lumatone mappings for 91edo and 93edo here from Keyboard Layout Lab/Various other Lumatone mappings: Lucius Chiaraviglio (talk) 06:17, 21 June 2025 (UTC)

Cantonismic-Werckismic rank-3 temperament Lumatone mappings

74edo (demonstrated to work but awaiting approval)

Bryan Deister has demonstrated the 7L 6s mapping of 74edo in microtonal improvisation in 74edo (2025). The rightward generator (8\74) functions as ~14/13; three of them make a classic major third ~5/4 (the cantonisma 10985/10976 is tempered out); five of them make an essentially-just undecimal subfifth ~16/11; and eight of them make a highly accurate undecimal supraminor seventh ~20/11. The upward generator (5\74) functions as ~21/20 and ~22/21 (the Werckisma (441/440 is tempered out); two of these make ~11/10; five of these make ~24/19 (which is distinguished from ~5/4); and eight of these make ~16/11. The range is about just over 3 octaves with no missing notes, and the octaves slope downward moderately, resulting in a vertical wraparound.

4
12
7
15
23
31
39
2
10
18
26
34
42
50
58
5
13
21
29
37
45
53
61
69
3
11
0
8
16
24
32
40
48
56
64
72
6
14
22
30
3
11
19
27
35
43
51
59
67
1
9
17
25
33
41
49
57
72
6
14
22
30
38
46
54
62
70
4
12
20
28
36
44
52
60
68
2
1
9
17
25
33
41
49
57
65
73
7
15
23
31
39
47
55
63
71
5
13
21
29
70
4
12
20
28
36
44
52
60
68
2
10
18
26
34
42
50
58
66
0
8
16
24
32
40
48
7
15
23
31
39
47
55
63
71
5
13
21
29
37
45
53
61
69
3
11
19
27
35
43
51
59
67
1
26
34
42
50
58
66
0
8
16
24
32
40
48
56
64
72
6
14
22
30
38
46
54
62
70
4
53
61
69
3
11
19
27
35
43
51
59
67
1
9
17
25
33
41
49
57
65
73
7
72
6
14
22
30
38
46
54
62
70
4
12
20
28
36
44
52
60
68
2
25
33
41
49
57
65
73
7
15
23
31
39
47
55
63
71
5
44
52
60
68
2
10
18
26
34
42
50
58
66
0
71
5
13
21
29
37
45
53
61
69
3
16
24
32
40
48
56
64
72
43
51
59
67
1
62
70

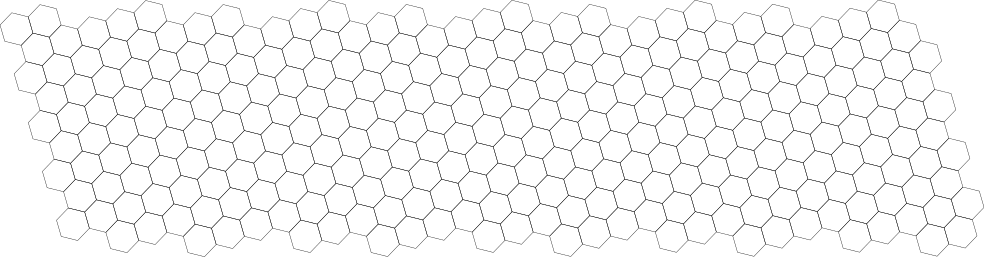
Added: Lucius Chiaraviglio (talk) 22:02, 12 June 2025 (UTC)
Last Modified: Lucius Chiaraviglio (talk) 22:17, 12 June 2025 (UTC)

Compton-related rank 3 temperament Lumatone mappings

96edo (demonstrated to work)

Bryan Deister has demonstrated a mapping for 96edo in which the rightward generator is 8\96 (~18/17) as in 12edo, while the upward generator is 7\96 (~20/19), in microtonal improvisation in 96edo (2025). The range is just over two octaves, with octaves sloping away and then wrapping around; on the other hand, it is easy to play eight 12edo subsets of 96edo that are displaced slightly from each other, as if one had eight pianos (even if of rather short compass) somehow all in reach at once. (Here, note 0 is in the middle of the left edge instead of Bryan Deister's usual lower left corner, to avoid skipping some of the bottom notes in the lowest note 0 to note 0 octave.) Although not shown in the video, this mapping also enables easy glissandos diagonally up-left or down-right.

12
20
13
21
29
37
45
6
14
22
30
38
46
54
62
7
15
23
31
39
47
55
63
71
79
87
0
8
16
24
32
40
48
56
64
72
80
88
0
8
1
9
17
25
33
41
49
57
65
73
81
89
1
9
17
25
33
90
2
10
18
26
34
42
50
58
66
74
82
90
2
10
18
26
34
42
50
91
3
11
19
27
35
43
51
59
67
75
83
91
3
11
19
27
35
43
51
59
67
75
84
92
4
12
20
28
36
44
52
60
68
76
84
92
4
12
20
28
36
44
52
60
68
76
84
92
93
5
13
21
29
37
45
53
61
69
77
85
93
5
13
21
29
37
45
53
61
69
77
85
93
5
13
21
14
22
30
38
46
54
62
70
78
86
94
6
14
22
30
38
46
54
62
70
78
86
94
6
14
22
39
47
55
63
71
79
87
95
7
15
23
31
39
47
55
63
71
79
87
95
7
15
23
56
64
72
80
88
0
8
16
24
32
40
48
56
64
72
80
88
0
8
16
81
89
1
9
17
25
33
41
49
57
65
73
81
89
1
9
17
2
10
18
26
34
42
50
58
66
74
82
90
2
10
27
35
43
51
59
67
75
83
91
3
11
44
52
60
68
76
84
92
4
69
77
85
93
5
86
94

Added: Lucius Chiaraviglio (talk) 07:40, 24 May 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 06:33, 26 May 2025 (UTC)

Meantone-related rank-3 Lumatone mappings

74edo (proposed but judged unsuitable)

An alternate 9L 4s mapping of 74edo is worthy of consideration. The rightward generator (6\74) functions as ~17/16 and ~18/17 (the semitonisma 289/288 is tempered out); two of them make a meantone whole tone (which functions as ~10/9, ~9/8, and ~19/17 — the syntonic comma 81/80, the ganassisma 153/152, and the malcolmisma 171/170 are all tempered out); three of them make the neogothic minor third ~13/11; four of them make the classic major third ~5/4; and six of them make the lesser septimal tritone ~7/5. The down-right generator (5\74) functions as ~21/20 and ~22/21 (the Werckisma (441/440 is tempered out); two of these make ~11/10; five of these make ~24/19 (which is distinguished from ~5/4); and eight of these make ~16/11. The stacking of two or four instances of ~3/2 (43\74) and octave-reducing also yields the same results as two or four instances (respectively) of the rightward generator, making this a meantone mapping as expected for the patent val of 74edo; yet the usefulness of the down-right generator for reaching higher-limit intervals is undeniable, making this a mapping for a Meantone-related rank-3 temperament in the 19-limit that is different from Didymus. The range is about 2⅔ octaves with no missing notes, less than Bryan Deister's Cantonismic-Werckismic detailed above, but the octaves slope downward only very gently, and include a few more duplicate notes which partially alleviate vertical wraparounds (in addition to the useful temperament properties detailed above). On the other hand, Bryan Deister has tried this mapping and reported that it is too spread out (challenging finger stretches).

66
72
71
3
9
15
21
70
2
8
14
20
26
32
38
1
7
13
19
25
31
37
43
49
55
61
0
6
12
18
24
30
36
42
48
54
60
66
72
4
5
11
17
23
29
35
41
47
53
59
65
71
3
9
15
21
27
4
10
16
22
28
34
40
46
52
58
64
70
2
8
14
20
26
32
38
44
9
15
21
27
33
39
45
51
57
63
69
1
7
13
19
25
31
37
43
49
55
61
67
8
14
20
26
32
38
44
50
56
62
68
0
6
12
18
24
30
36
42
48
54
60
66
72
4
10
19
25
31
37
43
49
55
61
67
73
5
11
17
23
29
35
41
47
53
59
65
71
3
9
15
21
27
33
36
42
48
54
60
66
72
4
10
16
22
28
34
40
46
52
58
64
70
2
8
14
20
26
32
38
59
65
71
3
9
15
21
27
33
39
45
51
57
63
69
1
7
13
19
25
31
37
43
2
8
14
20
26
32
38
44
50
56
62
68
0
6
12
18
24
30
36
42
25
31
37
43
49
55
61
67
73
5
11
17
23
29
35
41
47
42
48
54
60
66
72
4
10
16
22
28
34
40
46
65
71
3
9
15
21
27
33
39
45
51
8
14
20
26
32
38
44
50
31
37
43
49
55
48
54

Added: Lucius Chiaraviglio (talk) 07:00, 12 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 06:50, 26 June 2025 (UTC)

Unnamed rank-3 Lumatone mappings

75edo (demonstrated to work)

Bryan Deister has demonstrated the 7L 3s (step size ratio 9:4) Lumatone mapping for 75edo, in microtonal improvisation in 75edo (2025-06-24). So Right = 9\75 and down-right = 4\75, which means that Up = 5\75. Like 97edo, 75edo has mainly bad harmonics for its size (but with different harmonics being exceptions), so to find useful intervals, it is necessary to try to stick to primes 3, 5, and 23 (those having the least relative error) and/or take advantage of error cancellation as much as possible. Going right (9\75) 1 key is ~25/23 (error canceling, but starting out with some of the least bad harmonics); right 2 keys (18\75) is a subminor third ~625/529 (no simple ratio maps to this interval in the patent val of 75edo, but it merits mention anyway due to extensive use in the video); right 3 keys (27\75) = ~9/7 (errors only partially cancel, so somewhat flat); and right 7 keys (63\75) = ~34/19 (errors nearly cancel). Going down-right (4\75) 1 key functions as both ~27/26 and ~28/27; down-right 2 keys = ~14/13 (errors largely cancel), 3 keys = ~19/17 (errors largely cancel), and 5 keys = ~5/4 (the 5th harmonic has a small relative error). Going up (5\75) 1 key is ~23/22 (errors only partially canceling, so somewhat sharp). The range is just over 3½ octaves, and the octaves are very close to level, with just a slight down slope. This corresponds to the Neutral Thirds mapping on the Lumatone mapping for 75edo page.

2
11
6
15
24
33
42
1
10
19
28
37
46
55
64
5
14
23
32
41
50
59
68
2
11
20
0
9
18
27
36
45
54
63
72
6
15
24
33
42
4
13
22
31
40
49
58
67
1
10
19
28
37
46
55
64
73
74
8
17
26
35
44
53
62
71
5
14
23
32
41
50
59
68
2
11
20
3
12
21
30
39
48
57
66
0
9
18
27
36
45
54
63
72
6
15
24
33
42
51
73
7
16
25
34
43
52
61
70
4
13
22
31
40
49
58
67
1
10
19
28
37
46
55
64
73
11
20
29
38
47
56
65
74
8
17
26
35
44
53
62
71
5
14
23
32
41
50
59
68
2
11
20
29
33
42
51
60
69
3
12
21
30
39
48
57
66
0
9
18
27
36
45
54
63
72
6
15
24
33
64
73
7
16
25
34
43
52
61
70
4
13
22
31
40
49
58
67
1
10
19
28
37
11
20
29
38
47
56
65
74
8
17
26
35
44
53
62
71
5
14
23
32
42
51
60
69
3
12
21
30
39
48
57
66
0
9
18
27
36
64
73
7
16
25
34
43
52
61
70
4
13
22
31
20
29
38
47
56
65
74
8
17
26
35
42
51
60
69
3
12
21
30
73
7
16
25
34
20
29

Added: Lucius Chiaraviglio (talk) 07:46, 25 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 05:48, 29 June 2025 (UTC)

76edo (2 mappings demonstrated to work)

Bryan Deister has demonstrated an 8L 4s mapping for 76edo in microtonal improvisation in 76edo (2025), this version being the one with the 8:3 step ratio, as well as having successfully tested the 8L 4s version with the 7:5 step ratio (shown below the 8:3 step ration version). Although this is technically a Diminished layout (rank-2, with the quarter-octave at 19\76), it is probably more conveniently thought of as a rank-3 temperament layout. The rightward generator 8\76 is a near-just tridecimal 2/3-tone or trienthird, ~[[14/13]; three of these make a somewhat flat ~5/4 classic major third (the cantonisma 10985/10976 is tempered out); four of them (32\56) make the sharp (patent) version of the fourth ~4/3 (corresponding to the flat patent fifth ~3/2); seven of them (56\76) make a near-just classic major sixth ~5/3. Of the two single-key-step generators other than rightward, the upward generator 5\76 has a more convenient mapping than down-rightward (3\76); 5\76 is a slightly sharp greater vicesimotertial semitone ~[[23/22]; four of them make a near-just classic minor third ~[[6/5]. Eight rightward generators minus four upward generators reach the flat version of the fifth at 44\76 (the corresponding sharp fourth being reached with rightward generators alone, as noted above); five rightward generators plus one upward generator reach the sharp fifth, and two rightward generators plus three upward generators reach the corresponding flat fourth. The range is a bit under 3 octaves, and the octaves slope down mildly.

4
12
7
15
23
31
39
2
10
18
26
34
42
50
58
5
13
21
29
37
45
53
61
69
1
9
0
8
16
24
32
40
48
56
64
72
4
12
20
28
3
11
19
27
35
43
51
59
67
75
7
15
23
31
39
47
55
74
6
14
22
30
38
46
54
62
70
2
10
18
26
34
42
50
58
66
74
1
9
17
25
33
41
49
57
65
73
5
13
21
29
37
45
53
61
69
1
9
17
25
72
4
12
20
28
36
44
52
60
68
0
8
16
24
32
40
48
56
64
72
4
12
20
28
36
44
7
15
23
31
39
47
55
63
71
3
11
19
27
35
43
51
59
67
75
7
15
23
31
39
47
55
63
71
26
34
42
50
58
66
74
6
14
22
30
38
46
54
62
70
2
10
18
26
34
42
50
58
66
74
53
61
69
1
9
17
25
33
41
49
57
65
73
5
13
21
29
37
45
53
61
69
1
72
4
12
20
28
36
44
52
60
68
0
8
16
24
32
40
48
56
64
72
23
31
39
47
55
63
71
3
11
19
27
35
43
51
59
67
75
42
50
58
66
74
6
14
22
30
38
46
54
62
70
69
1
9
17
25
33
41
49
57
65
73
12
20
28
36
44
52
60
68
39
47
55
63
71
58
66

Bryan Deister has also tested a version of the 8L 4s mapping for 76edo that has a 7:5 step ratio, but no demonstration video is available at this time. As with the 8:3 step ratio version, this is probably more conveniently thought of as a rank-3 temperament layout than a Diminished temperament layout. The rightward generator 7\76 is a flat septimal major semitone ~15/14; it also functions as a near-just classic diatonic semitone ~16/15, but only if the sharp fifth (76b val) is used (which tempers out the marvel comma 225/224); five of these make a near-just undecimal major fourth ~11/8; eight of them make a near-just classic major sixth ~5/3. Of the two single-key-step generators other than rightward, the down-right generator 5\76 has the attraction (for anyone trying out both versions of the 8L 4s mapping) of being the same as the upward generator for the 8:3 step ratio mapping; further, when used with the 7:5 step ratio mapping, its alignment with the small step scale provides added convenience, since one does not have to count chromas separately from small steps. Five (large) steps right plus two (small) steps down-right yields the sharp version of the fifth (45\76); three (large) steps right plus two (small) steps down-right yields the corresponding flat version of the fourth, putting it in the same row as the sharp fifth and the classic major third, which is one (large) step left of the flat fourth. Seven (large) steps right minus one (small) step down-right (thus plus one step up-left) yields the flat version of the fifth (44\76), while six (large) steps right minus two (small) steps down-right (thus plus two steps up-left) yields the corresponding sharp version of the fourth (32\76). The range is a bit under 3 octaves, and the octaves slope down mildly.

70
1
75
6
13
20
27
73
4
11
18
25
32
39
46
2
9
16
23
30
37
44
51
58
65
72
0
7
14
21
28
35
42
49
56
63
70
1
8
15
5
12
19
26
33
40
47
54
61
68
75
6
13
20
27
34
41
3
10
17
24
31
38
45
52
59
66
73
4
11
18
25
32
39
46
53
60
8
15
22
29
36
43
50
57
64
71
2
9
16
23
30
37
44
51
58
65
72
3
10
6
13
20
27
34
41
48
55
62
69
0
7
14
21
28
35
42
49
56
63
70
1
8
15
22
29
18
25
32
39
46
53
60
67
74
5
12
19
26
33
40
47
54
61
68
75
6
13
20
27
34
41
48
55
37
44
51
58
65
72
3
10
17
24
31
38
45
52
59
66
73
4
11
18
25
32
39
46
53
60
63
70
1
8
15
22
29
36
43
50
57
64
71
2
9
16
23
30
37
44
51
58
65
6
13
20
27
34
41
48
55
62
69
0
7
14
21
28
35
42
49
56
63
32
39
46
53
60
67
74
5
12
19
26
33
40
47
54
61
68
51
58
65
72
3
10
17
24
31
38
45
52
59
66
1
8
15
22
29
36
43
50
57
64
71
20
27
34
41
48
55
62
69
46
53
60
67
74
65
72

Added: Lucius Chiaraviglio (talk) 07:19, 27 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:02, 2 July 2025 (UTC)

91edo (demonstrated to work)

Bryan Deister has demonstrated an isomorphic 9L 2s mapping for 91edo in improv 91edo (2025). The range is just one note beyond 3 full octaves, with octaves sloping up mildly (which results in a wraparound of note 0). The rightward generator 9\91 is the septimal diatonic semitone ~15/14. The upward generator 4\91 is a quartertone that functions as ~32/31, ~33/32, ~34/33, and ~36/35; two of them make the minor diatonic semitone ~17/16; six of them make a near-just minor third ~6/5. The use of this generator makes this a mapping for Quartkeenlig; however, since stacking the upward generator quickly leads to wraparounds, and attempting to get the perfect fifth in 91edo with this generator yields 52\91, which is the 7edo (91bb) fifth. Therefore, this mapping really needs to be treated as a rank-3 temperament mapping; for instance, to get the patent fifth 53\92 (a mildly flat ~3/2, almost exactly 1/7-comma meantone), it is easiest to stack five rightward generators and two upward generators.

0
9
5
14
23
32
41
1
10
19
28
37
46
55
64
6
15
24
33
42
51
60
69
78
87
5
2
11
20
29
38
47
56
65
74
83
1
10
19
28
7
16
25
34
43
52
61
70
79
88
6
15
24
33
42
51
60
3
12
21
30
39
48
57
66
75
84
2
11
20
29
38
47
56
65
74
83
8
17
26
35
44
53
62
71
80
89
7
16
25
34
43
52
61
70
79
88
6
15
24
4
13
22
31
40
49
58
67
76
85
3
12
21
30
39
48
57
66
75
84
2
11
20
29
38
47
18
27
36
45
54
63
72
81
90
8
17
26
35
44
53
62
71
80
89
7
16
25
34
43
52
61
70
79
41
50
59
68
77
86
4
13
22
31
40
49
58
67
76
85
3
12
21
30
39
48
57
66
75
84
73
82
0
9
18
27
36
45
54
63
72
81
90
8
17
26
35
44
53
62
71
80
89
5
14
23
32
41
50
59
68
77
86
4
13
22
31
40
49
58
67
76
85
37
46
55
64
73
82
0
9
18
27
36
45
54
63
72
81
90
60
69
78
87
5
14
23
32
41
50
59
68
77
86
1
10
19
28
37
46
55
64
73
82
0
24
33
42
51
60
69
78
87
56
65
74
83
1
79
88

Added: Lucius Chiaraviglio (talk) 16:02, 4 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:57, 23 June 2025 (UTC)

93edo (demonstrated to work)

(This mapping has been updated with the changes made to the official version by Yourmusic Productions and ArrowHead294.)

Bryan Deister has demonstrated a mapping for 93edo in microtonal improvisation in 93edo (2025). The rightward generator 6\93 represents 21/20, 23/22, and 25/24, producing a 15L 1s scale as in Valentine, although 93edo is contorted with this scale (L = 6 and s = 3) and temperament; choosing the scale 13L 3s avoids contortion, although neither the bright version (64\93) nor the dark version (29\93) of its generator maps to a convenient ratio, so the following discussion instead uses the generators for the mapping itself. Going right 2 keys makes a ~35/32 neutral second (abundantly used in the later part of the video); 3 right = ~8/7; 5 right = ~5/4; and 8 right = ~10/7. To avoid contortion, it is necessary to use a second generator, making this a rank-3 temperament mapping; the upward generator 7\93 is ~20/19; 4 steps up makes ~16/13; 5 steps up makes ~13/10, and 9 steps up (which always involves a vertical wraparound) makes ~8/5. Down-right is −1\93, enabling easy glissandos (demonstrated in the beginning of the video). In order to avoid having notes of the first note 0 to note 0 octave chopped off at the left edge, the first note 5 is placed half way down the left edge, and note 0 is 5 down-right from that. The range is just over an octave and a half, and the octaves slope from near to far.

21
27
20
26
32
38
44
13
19
25
31
37
43
49
55
12
18
24
30
36
42
48
54
60
66
72
5
11
17
23
29
35
41
47
53
59
65
71
77
83
4
10
16
22
28
34
40
46
52
58
64
70
76
82
88
1
7
90
3
9
15
21
27
33
39
45
51
57
63
69
75
81
87
0
6
12
18
89
2
8
14
20
26
32
38
44
50
56
62
68
74
80
86
92
5
11
17
23
29
35
82
88
1
7
13
19
25
31
37
43
49
55
61
67
73
79
85
91
4
10
16
22
28
34
40
46
87
0
6
12
18
24
30
36
42
48
54
60
66
72
78
84
90
3
9
15
21
27
33
39
45
51
57
63
5
11
17
23
29
35
41
47
53
59
65
71
77
83
89
2
8
14
20
26
32
38
44
50
56
62
22
28
34
40
46
52
58
64
70
76
82
88
1
7
13
19
25
31
37
43
49
55
61
33
39
45
51
57
63
69
75
81
87
0
6
12
18
24
30
36
42
48
54
50
56
62
68
74
80
86
92
5
11
17
23
29
35
41
47
53
61
67
73
79
85
91
4
10
16
22
28
34
40
46
78
84
90
3
9
15
21
27
33
39
45
89
2
8
14
20
26
32
38
13
19
25
31
37
24
30

Added: Lucius Chiaraviglio (talk) 20:43, 31 May 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:57, 14 June 2025 (UTC)

98edo (proposed and untested)

(Descriptive text needs to go here for 98edo, starting with rightward generator 9\98 = ~16/15 and 5 of them = ~11/8; and upward generator 5\98 = both ~29/28 ~30/29 and 9 of them = ~11/8; may need to streamline down to rank-2.)

4
13
8
17
26
35
44
3
12
21
30
39
48
57
66
7
16
25
34
43
52
61
70
79
88
97
2
11
20
29
38
47
56
65
74
83
92
3
12
21
6
15
24
33
42
51
60
69
78
87
96
7
16
25
34
43
52
1
10
19
28
37
46
55
64
73
82
91
2
11
20
29
38
47
56
65
74
5
14
23
32
41
50
59
68
77
86
95
6
15
24
33
42
51
60
69
78
87
96
7
0
9
18
27
36
45
54
63
72
81
90
1
10
19
28
37
46
55
64
73
82
91
2
11
20
29
13
22
31
40
49
58
67
76
85
94
5
14
23
32
41
50
59
68
77
86
95
6
15
24
33
42
51
60
35
44
53
62
71
80
89
0
9
18
27
36
45
54
63
72
81
90
1
10
19
28
37
46
55
64
66
75
84
93
4
13
22
31
40
49
58
67
76
85
94
5
14
23
32
41
50
59
68
88
97
8
17
26
35
44
53
62
71
80
89
0
9
18
27
36
45
54
63
21
30
39
48
57
66
75
84
93
4
13
22
31
40
49
58
67
43
52
61
70
79
88
97
8
17
26
35
44
53
62
74
83
92
3
12
21
30
39
48
57
66
96
7
16
25
34
43
52
61
29
38
47
56
65
51
60

Added: Lucius Chiaraviglio (talk) 07:52, 21 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:57, 23 June 2025 (UTC)

99edo (proposed and untested)

(Descriptive text needs to go here for 99edo, starting with rightward generator 8\99 = ~135/128, ~18/17, ~19/18, and 3 of them make ~13/11, and 4 of them make ~5/4and 6 of them make ~7/5; and upward generator 1\99 = ~126/125; may need to streamline down to rank-2.)

75
83
82
90
98
7
15
81
89
97
6
14
22
30
38
88
96
5
13
21
29
37
45
53
61
69
87
95
4
12
20
28
36
44
52
60
68
76
84
92
94
3
11
19
27
35
43
51
59
67
75
83
91
0
8
16
24
93
2
10
18
26
34
42
50
58
66
74
82
90
98
7
15
23
31
39
47
1
9
17
25
33
41
49
57
65
73
81
89
97
6
14
22
30
38
46
54
62
70
78
0
8
16
24
32
40
48
56
64
72
80
88
96
5
13
21
29
37
45
53
61
69
77
85
93
2
15
23
31
39
47
55
63
71
79
87
95
4
12
20
28
36
44
52
60
68
76
84
92
1
9
17
25
33
38
46
54
62
70
78
86
94
3
11
19
27
35
43
51
59
67
75
83
91
0
8
16
24
32
40
69
77
85
93
2
10
18
26
34
42
50
58
66
74
82
90
98
7
15
23
31
39
47
92
1
9
17
25
33
41
49
57
65
73
81
89
97
6
14
22
30
38
46
24
32
40
48
56
64
72
80
88
96
5
13
21
29
37
45
53
47
55
63
71
79
87
95
4
12
20
28
36
44
52
78
86
94
3
11
19
27
35
43
51
59
2
10
18
26
34
42
50
58
33
41
49
57
65
56
64

Added: Lucius Chiaraviglio (talk) 07:52, 21 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:57, 23 June 2025 (UTC)

100edo (proposed and untested)

(Descriptive text needs to go here for 100edom starting with rightward generator 8\100 = ~37/35, and 2 of them make ~19/17, and 3 of them make ~13/11, and 4 of them make ~5/4; upward generator 1\100 = ?; cannot streamline down to rank-2.)

76
84
83
91
99
7
15
82
90
98
6
14
22
30
38
89
97
5
13
21
29
37
45
53
61
69
88
96
4
12
20
28
36
44
52
60
68
76
84
92
95
3
11
19
27
35
43
51
59
67
75
83
91
99
7
15
23
94
2
10
18
26
34
42
50
58
66
74
82
90
98
6
14
22
30
38
46
1
9
17
25
33
41
49
57
65
73
81
89
97
5
13
21
29
37
45
53
61
69
77
0
8
16
24
32
40
48
56
64
72
80
88
96
4
12
20
28
36
44
52
60
68
76
84
92
0
15
23
31
39
47
55
63
71
79
87
95
3
11
19
27
35
43
51
59
67
75
83
91
99
7
15
23
31
38
46
54
62
70
78
86
94
2
10
18
26
34
42
50
58
66
74
82
90
98
6
14
22
30
38
69
77
85
93
1
9
17
25
33
41
49
57
65
73
81
89
97
5
13
21
29
37
45
92
0
8
16
24
32
40
48
56
64
72
80
88
96
4
12
20
28
36
44
23
31
39
47
55
63
71
79
87
95
3
11
19
27
35
43
51
46
54
62
70
78
86
94
2
10
18
26
34
42
50
77
85
93
1
9
17
25
33
41
49
57
0
8
16
24
32
40
48
56
31
39
47
55
63
54
62

Added: Lucius Chiaraviglio (talk) 07:52, 21 June 2025 (UTC)
Last modified: Lucius Chiaraviglio (talk) 08:57, 23 June 2025 (UTC)

Retrieved from "https://en.xen.wiki/index.php?title=User:Lucius_Chiaraviglio/Keyboard_Layout_Lab/Various_rank-3_temperament_Lumatone_mappings&oldid=204018"