11-limit: Difference between revisions
mNo edit summary |
reworked (some intersections with 11-odd-limit found -> todo) |
||
| Line 1: | Line 1: | ||
The ''11-limit'' consists of all [[ | The '''11-limit''' consists of all [[Just intonation|justly tuned]] intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are [[14/11]], [[11/8]], [[27/22]] and [[99/98]]. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances. | ||
{| class="wikitable" | == Intervals 1 == | ||
{| class="wikitable center-all" | |||
! Ratio | |||
! colspan="2" | [[Color name]] | |||
! harmonic solfege | |||
|- | |- | ||
| 12/11 | |||
| 1u2 | |||
| lu 2nd | |||
| fu-sol | |||
|- | |- | ||
| | | 11/10 | ||
| | | 1og2 | ||
| | | logu 2nd | ||
| | | mi-fu | ||
|- | |- | ||
| | | 10/9 | ||
| | | y2 | ||
| | | yo 2nd | ||
| | | re-mi | ||
|- | |- | ||
| | | 9/8 | ||
| | | w2 | ||
| | | wa 2nd | ||
| | | do-re | ||
|- | |- | ||
| | | 8/7 | ||
| | | r2 | ||
| | | ru 2nd | ||
| | | ta-do | ||
|- | |- | ||
| | | 7/6 | ||
| | | z3 | ||
| | | zo 3rd | ||
| | | sol-ta | ||
|- | |- | ||
| | | 6/5 | ||
| | | g3 | ||
| | | gu 3rd | ||
| | | mi-sol, ti-re | ||
|- | |- | ||
| | | 11/9 | ||
| | | 1o3 | ||
| | | ilo 3rd | ||
| | | re-fu | ||
|- | |- | ||
| | | 5/4 | ||
| | | y3 | ||
| | | yo 3rd | ||
| | | do-mi | ||
|- | |- | ||
| | | 14/11 | ||
| | | 1uz4 | ||
| | | luzo 4th | ||
| | | fu-ta | ||
|- | |- | ||
| | | 9/7 | ||
| | | r3 | ||
| | | ru 3rd | ||
| | | ta-re | ||
|- | |- | ||
| | | 4/3 | ||
| | | w4 | ||
| | | wa 4th | ||
| | | do-fa | ||
|- | |- | ||
| | | 11/8 | ||
| | | 1o4 | ||
| | | ilo 4th | ||
| do-fu | |||
|- | |- | ||
| | | 7/5 | ||
| | | zg5 | ||
| | | zogu 5th | ||
| | | mi-ta | ||
|- | |- | ||
| | | 10/7 | ||
| | | ry4 | ||
| | | ruyo 4th | ||
| | | ta-mi | ||
|- | |- | ||
| | | 16/11 | ||
| | | 1u5 | ||
| | | lu 5th | ||
| | | fu-do | ||
|- | |- | ||
| | | 3/2 | ||
| | | w5 | ||
| | | wa 5th | ||
| | | do-sol | ||
|- | |- | ||
| | | 14/9 | ||
| | | z6 | ||
| | | zo 6th | ||
| | | re-ta | ||
|- | |- | ||
| | | 11/7 | ||
| | | 1or5 | ||
| | | loru 5th | ||
| | | ta-fu | ||
|- | |- | ||
| | | 8/5 | ||
| | | g6 | ||
| | | gu 6th | ||
| | | mi-do | ||
|- | |- | ||
| | | 18/11 | ||
| | | 1u6 | ||
| | | lu 6th | ||
| | | fu-re | ||
|- | |- | ||
| | | 5/3 | ||
| | | y6 | ||
| | | yo 6th | ||
| | | sol-mi | ||
|- | |- | ||
| | | 12/7 | ||
| | | r6 | ||
| | | ru 6th | ||
| | | ta-sol | ||
|- | |- | ||
| | | 7/4 | ||
| | | z7 | ||
| | | zo 7th | ||
| | | do-ta | ||
|- | |- | ||
| | | 16/9 | ||
| | | w7 | ||
| | | wa 7th | ||
| | | re-do | ||
|- | |- | ||
| | | 9/5 | ||
| | | g7 | ||
| | | gu 7th | ||
| | | mi-re | ||
|- | |- | ||
| | | 20/11 | ||
| | | 1uy7 | ||
| | | luyo 7th | ||
| | | fu-mi | ||
|- | |- | ||
| | | 11/6 | ||
| | | 1o7 | ||
| | | ilo 7th | ||
| | | sol-fu | ||
|- | |- | ||
| 2/1 | |||
| w8 | |||
| wa 8ve | |||
| do-do | |||
|w8 | |||
|wa 8ve | |||
|} | |} | ||
While the [[ | While the [[7-limit]] introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of [[12edo]], the 11-limit introduces neutral intervals, [[superfourth]]s and [[subfifth]]s, which fall in between major, minor and perfect [[interval category|interval categories]] and thus demand new distinctions. It is thus inescapably xenharmonic. | ||
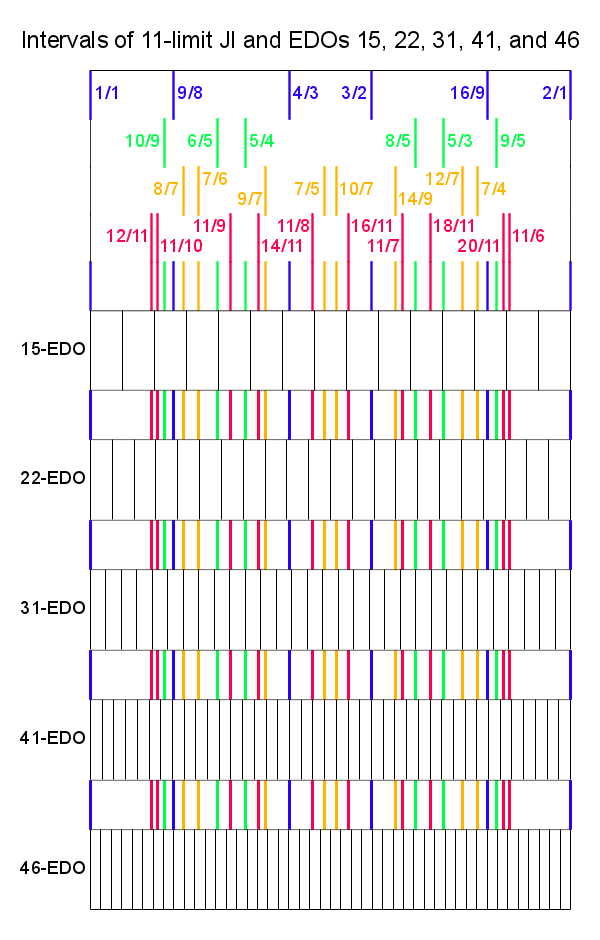
Relative to their size, [[EDO | Relative to their size, [[EDO]]s which do (relatively) well in supporting 11-limit intervals are: {{EDOs| 1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 15, 22, 26, 31, 41, 63, 72, 87, 109, and 161edo }}. | ||
[[File:11-limit_compare.png|alt=11-limit_compare.png|11-limit_compare.png]] | [[File:11-limit_compare.png|alt=11-limit_compare.png|11-limit_compare.png]] | ||
==Intervals== | == Intervals 2 == | ||
Here are all the 15-odd-limit intervals of 11: | Here are all the 15-odd-limit intervals of 11: | ||
{| class="wikitable" | {| class="wikitable center-all right-2" | ||
! Ratio | |||
! | ! Site ([[cents|¢]]) | ||
! | | ! colspan="2" | [[Color name]] | ||
! | |||
|- | |- | ||
| [[12/11]] | |||
| 150.637 | |||
|1u2 | | 1u2 | ||
|lu 2nd | | lu 2nd | ||
|- | |- | ||
| [[11/10]] | |||
| 165.004 | |||
|1og2 | | 1og2 | ||
|logu 2nd | | logu 2nd | ||
|- | |- | ||
| [[11/9]] | |||
| 347.408 | |||
|1o3 | | 1o3 | ||
|ilo 3rd | | ilo 3rd | ||
|- | |- | ||
| [[14/11]] | |||
| 417.508 | |||
|1uz4 | | 1uz4 | ||
|lu 4th | | lu 4th | ||
|- | |- | ||
| [[15/11]] | |||
| 536.951 | |||
|1uy4 | | 1uy4 | ||
|luyo 4th | | luyo 4th | ||
|- | |- | ||
| [[11/8]] | |||
| 551.318 | |||
|1o4 | | 1o4 | ||
|ilo 4th | | ilo 4th | ||
|- | |- | ||
| [[16/11]] | |||
| 648.682 | |||
|1u5 | | 1u5 | ||
|lu 5th | | lu 5th | ||
|- | |- | ||
| [[22/15]] | |||
| 663.049 | |||
|1og5 | | 1og5 | ||
|logu 5th | | logu 5th | ||
|- | |- | ||
| [[11/7]] | |||
| 782.492 | |||
|1or5 | | 1or5 | ||
|loru 5th | | loru 5th | ||
|- | |- | ||
| [[18/11]] | |||
| 852.592 | |||
|1u6 | | 1u6 | ||
|lu 6th | | lu 6th | ||
|- | |- | ||
| [[20/11]] | |||
| 1034.996 | |||
|1uy7 | | 1uy7 | ||
|luyo 7th | | luyo 7th | ||
|- | |- | ||
| [[11/6]] | |||
| 1049.363 | |||
|1o7 | | 1o7 | ||
|ilo 7th | | ilo 7th | ||
|} | |} | ||
=Music= | == Music == | ||
[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Brief 11-ratio composition] [http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3 play] by Dave Hill | * [http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Study #3] [http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3 play] by [[Dave Hill]] | ||
* [http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Brief 11-ratio composition] [http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3 play] by Dave Hill | |||
* [http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3 11 Limit Piano] by [[Chris Vaisvil]] | |||
* [https://soundcloud.com/andrew_heathwaite/11-limit-singtervals 11-limit singtervals] by [[Andrew Heathwaite]] | |||
== See also == | |||
[ | * [[Gallery of just intervals]] | ||
* [[Harmonic limit]] | |||
* [[11-odd-limit]] | |||
[[ | |||
[[Category:11-limit]] | [[Category:11-limit]] | ||
| Line 248: | Line 249: | ||
[[Category:listen]] | [[Category:listen]] | ||
[[Category:prime_limit]] | [[Category:prime_limit]] | ||
[[Category:Todo]] | |||
Revision as of 20:07, 10 June 2020
The 11-limit consists of all justly tuned intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are 14/11, 11/8, 27/22 and 99/98. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.
Intervals 1
| Ratio | Color name | harmonic solfege | |
|---|---|---|---|
| 12/11 | 1u2 | lu 2nd | fu-sol |
| 11/10 | 1og2 | logu 2nd | mi-fu |
| 10/9 | y2 | yo 2nd | re-mi |
| 9/8 | w2 | wa 2nd | do-re |
| 8/7 | r2 | ru 2nd | ta-do |
| 7/6 | z3 | zo 3rd | sol-ta |
| 6/5 | g3 | gu 3rd | mi-sol, ti-re |
| 11/9 | 1o3 | ilo 3rd | re-fu |
| 5/4 | y3 | yo 3rd | do-mi |
| 14/11 | 1uz4 | luzo 4th | fu-ta |
| 9/7 | r3 | ru 3rd | ta-re |
| 4/3 | w4 | wa 4th | do-fa |
| 11/8 | 1o4 | ilo 4th | do-fu |
| 7/5 | zg5 | zogu 5th | mi-ta |
| 10/7 | ry4 | ruyo 4th | ta-mi |
| 16/11 | 1u5 | lu 5th | fu-do |
| 3/2 | w5 | wa 5th | do-sol |
| 14/9 | z6 | zo 6th | re-ta |
| 11/7 | 1or5 | loru 5th | ta-fu |
| 8/5 | g6 | gu 6th | mi-do |
| 18/11 | 1u6 | lu 6th | fu-re |
| 5/3 | y6 | yo 6th | sol-mi |
| 12/7 | r6 | ru 6th | ta-sol |
| 7/4 | z7 | zo 7th | do-ta |
| 16/9 | w7 | wa 7th | re-do |
| 9/5 | g7 | gu 7th | mi-re |
| 20/11 | 1uy7 | luyo 7th | fu-mi |
| 11/6 | 1o7 | ilo 7th | sol-fu |
| 2/1 | w8 | wa 8ve | do-do |
While the 7-limit introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of 12edo, the 11-limit introduces neutral intervals, superfourths and subfifths, which fall in between major, minor and perfect interval categories and thus demand new distinctions. It is thus inescapably xenharmonic.
Relative to their size, EDOs which do (relatively) well in supporting 11-limit intervals are: 1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 15, 22, 26, 31, 41, 63, 72, 87, 109, and 161edo.
Intervals 2
Here are all the 15-odd-limit intervals of 11:
| Ratio | Site (¢) | Color name | |
|---|---|---|---|
| 12/11 | 150.637 | 1u2 | lu 2nd |
| 11/10 | 165.004 | 1og2 | logu 2nd |
| 11/9 | 347.408 | 1o3 | ilo 3rd |
| 14/11 | 417.508 | 1uz4 | lu 4th |
| 15/11 | 536.951 | 1uy4 | luyo 4th |
| 11/8 | 551.318 | 1o4 | ilo 4th |
| 16/11 | 648.682 | 1u5 | lu 5th |
| 22/15 | 663.049 | 1og5 | logu 5th |
| 11/7 | 782.492 | 1or5 | loru 5th |
| 18/11 | 852.592 | 1u6 | lu 6th |
| 20/11 | 1034.996 | 1uy7 | luyo 7th |
| 11/6 | 1049.363 | 1o7 | ilo 7th |
Music
- Study #3 play by Dave Hill
- Brief 11-ratio composition play by Dave Hill
- 11 Limit Piano by Chris Vaisvil
- 11-limit singtervals by Andrew Heathwaite