Miracle: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Wikispaces>keenanpepper
**Imported revision 381128200 - Original comment: **
m →Music: cleanup
 
(54 intermediate revisions by 13 users not shown)
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
[[de:Miracle]]
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
{{Wikipedia|Miracle temperament}}
: This revision was by author [[User:keenanpepper|keenanpepper]] and made on <tt>2012-11-10 16:24:00 UTC</tt>.<br>
'''Miracle''' is a [[regular temperament]] discovered by [[George Secor]] in 1974 which splits a tempered [[3/2]] into six [[generator]]s, called ''[[secor]]s'' (after George), that serve as both [[15/14]] and [[16/15]] semitones. A stack of two generators represents [[8/7]], and a stack of seven generators represents [[8/5]]. It is a member of both the [[marvel temperaments]], by [[tempering out]] [[225/224]], and the [[gamelismic clan]], by tempering out [[1029/1024]]. It extends naturally to the [[11-limit]] by treating the neutral third from three generators as [[11/9]], tempering out [[243/242]], [[385/384]], [[441/440]], and [[540/539]].  
: The original revision id was <tt>381128200</tt>.<br>
: The revision comment was: <tt></tt><br>
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">Miracle is an exceptionally efficient linear temperament which is a member of both the [[marvel temperaments]] and the [[gamelismic clan]]. It is quite accurate, with TOP error only 0.63 cents/octave, meaning intervals of the 11-limit tonality diamond are represented with only one or two cents of error. Yet it is also very "low complexity" (efficient), as evidenced by the high density of 11-odd-limit ratios (in bold) in the following table:
|| # of secors || 0 || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 ||
|| JI intervals represented || **1/1** || 16/15~15/14 || **8/7** || **11/9** || 21/16 || **7/5** || **3/2** || **8/5** || **12/7** || **11/6** ||
|| # of secors || 10 || 11 || 12 || 13 || 14 || 15 || 16 || 17 || 18 || 19 ||
|| JI intervals represented || 63/32~55/28~108/55~49/25~96/49~88/45 || 22/21~21/20 || **9/8** || **6/5** || **9/7** || **11/8** || 22/15 || **11/7** || 42/25 || **9/5** ||
|| # of secors || 20 || 21 || 22 ||  ||  ||  ||  ||  ||  ||  ||
|| JI intervals represented || 48/25 ||  || **11/10** ||  ||  ||  ||  ||  ||  ||  ||
Some temperaments have 11/9 as a "neutral third", meaning it's exactly half of a 3/2 (tempering out 243/242), and other temperaments (in the [[gamelismic clan]]) have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts. This is in fact the generator of miracle temperament, called a "secor", and it represents both 16/15 and 15/14.


Miracle can also be thought of as a [[cluster temperament]] with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing 45/44~49/48~50/49~55/54~56/55~64/63 all tempered together.
Miracle is an exceptionally efficient linear temperament. It is quite accurate, with [[TOP]] error only 0.63 [[cent]]s/[[octave]], meaning intervals of the [[11-odd-limit]] [[tonality diamond]] are represented with only one or two cents of error. Yet it is also very low-complexity (efficient), as evidenced by the high density of 11-odd-limit ratios in the [[#Interval chain]]. At least one inversion of every interval in the 11-odd-limit tonality diamond is represented within 22 secors of the starting value.  


=Spectrum of Miracle Tunings by Eigenmonzos=
Some temperaments have 11/9 as a neutral third, meaning it is exactly half of a 3/2 (tempering out 243/242), and other temperaments have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts.  
||~ Eigenmonzo ||~ Secor ||
|| 8/7 || 115.587 ||
|| 11/9 || 115.803 ||
|| 5/4 || 116.241 ||
|| 7/5 || 116.502 ||
|| 6/5 || 116.588 (5 and 7 limit minimax) ||
|| 11/10 || 116.591 ||
|| 12/11 || 116.596 ||
|| 14/11 || 116.617 ||
|| 7/6 || 116.641 ||
|| 10/9 || 116.716 (9 and 11 limit minimax, Secor's definition of secor) ||
|| 11/8 || 116.755 ||
|| 9/7 || 116.792 ||
|| 4/3 || 116.993 ||</pre></div>
<h4>Original HTML content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;Miracle&lt;/title&gt;&lt;/head&gt;&lt;body&gt;Miracle is an exceptionally efficient linear temperament which is a member of both the &lt;a class="wiki_link" href="/marvel%20temperaments"&gt;marvel temperaments&lt;/a&gt; and the &lt;a class="wiki_link" href="/gamelismic%20clan"&gt;gamelismic clan&lt;/a&gt;. It is quite accurate, with TOP error only 0.63 cents/octave, meaning intervals of the 11-limit tonality diamond are represented with only one or two cents of error. Yet it is also very &amp;quot;low complexity&amp;quot; (efficient), as evidenced by the high density of 11-odd-limit ratios (in bold) in the following table:&lt;br /&gt;


Miracle can also be thought of as a [[cluster temperament]] with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing [[45/44]] ~ [[49/48]] ~ [[50/49]] ~ [[55/54]] ~ [[56/55]] ~ [[64/63]] all [[tempered]] together.


&lt;table class="wiki_table"&gt;
See [[Miracle extensions]] for [[13-limit]] and [[17-limit]] extensions. See [[Gamelismic clan #Miracle]] for technical data.
    &lt;tr&gt;
        &lt;td&gt;&lt;ol&gt;&lt;li&gt;of secors&lt;/li&gt;&lt;/ol&gt;&lt;/td&gt;
        &lt;td&gt;0&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;1&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;2&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;3&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;4&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;5&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;6&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;8&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;9&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;JI intervals represented&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;1/1&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;16/15~15/14&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;8/7&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;11/9&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;21/16&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;7/5&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;3/2&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;8/5&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;12/7&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;11/6&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;ol&gt;&lt;li&gt;of secors&lt;/li&gt;&lt;/ol&gt;&lt;/td&gt;
        &lt;td&gt;10&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;12&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;13&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;14&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;15&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;16&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;17&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;18&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;19&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;JI intervals represented&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;63/32~55/28~108/55~49/25~96/49~88/45&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;22/21~21/20&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;9/8&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;6/5&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;9/7&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;11/8&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;22/15&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;11/7&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;42/25&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;9/5&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;ol&gt;&lt;li&gt;of secors&lt;/li&gt;&lt;/ol&gt;&lt;/td&gt;
        &lt;td&gt;20&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;21&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;22&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;JI intervals represented&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;48/25&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;strong&gt;11/10&lt;/strong&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
&lt;/table&gt;


Some temperaments have 11/9 as a &amp;quot;neutral third&amp;quot;, meaning it's exactly half of a 3/2 (tempering out 243/242), and other temperaments (in the &lt;a class="wiki_link" href="/gamelismic%20clan"&gt;gamelismic clan&lt;/a&gt;) have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts. This is in fact the generator of miracle temperament, called a &amp;quot;secor&amp;quot;, and it represents both 16/15 and 15/14.&lt;br /&gt;
== Interval chain ==
&lt;br /&gt;
In the following table, odd harmonics and subharmonics 1–21 are labeled in '''bold'''.  
Miracle can also be thought of as a &lt;a class="wiki_link" href="/cluster%20temperament"&gt;cluster temperament&lt;/a&gt; with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing 45/44~49/48~50/49~55/54~56/55~64/63 all tempered together.&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:0:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc0"&gt;&lt;a name="Spectrum of Miracle Tunings by Eigenmonzos"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:0 --&gt;Spectrum of Miracle Tunings by Eigenmonzos&lt;/h1&gt;


&lt;table class="wiki_table"&gt;
{| class="wikitable center-1 right-2"
    &lt;tr&gt;
|-
        &lt;th&gt;Eigenmonzo&lt;br /&gt;
! #
&lt;/th&gt;
! Cents*
        &lt;th&gt;Secor&lt;br /&gt;
! Approximate ratios
&lt;/th&gt;
|-
    &lt;/tr&gt;
| 0
    &lt;tr&gt;
| 0.0
        &lt;td&gt;8/7&lt;br /&gt;
| '''1/1'''
&lt;/td&gt;
|-
        &lt;td&gt;115.587&lt;br /&gt;
| 1
&lt;/td&gt;
| 116.6
    &lt;/tr&gt;
| 15/14, '''16/15'''
    &lt;tr&gt;
|-
        &lt;td&gt;11/9&lt;br /&gt;
| 2
&lt;/td&gt;
| 233.3
        &lt;td&gt;115.803&lt;br /&gt;
| '''8/7'''
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 3
    &lt;tr&gt;
| 349.9
        &lt;td&gt;5/4&lt;br /&gt;
| 11/9
&lt;/td&gt;
|-
        &lt;td&gt;116.241&lt;br /&gt;
| 4
&lt;/td&gt;
| 466.6
    &lt;/tr&gt;
| '''21/16'''
    &lt;tr&gt;
|-
        &lt;td&gt;7/5&lt;br /&gt;
| 5
&lt;/td&gt;
| 583.2
        &lt;td&gt;116.502&lt;br /&gt;
| 7/5
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 6
    &lt;tr&gt;
| 699.9
        &lt;td&gt;6/5&lt;br /&gt;
| '''3/2'''
&lt;/td&gt;
|-
        &lt;td&gt;116.588 (5 and 7 limit minimax)&lt;br /&gt;
| 7
&lt;/td&gt;
| 816.5
    &lt;/tr&gt;
| '''8/5'''
    &lt;tr&gt;
|-
        &lt;td&gt;11/10&lt;br /&gt;
| 8
&lt;/td&gt;
| 933.2
        &lt;td&gt;116.591&lt;br /&gt;
| 12/7
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 9
    &lt;tr&gt;
| 1049.8
        &lt;td&gt;12/11&lt;br /&gt;
| 11/6
&lt;/td&gt;
|-
        &lt;td&gt;116.596&lt;br /&gt;
| 10
&lt;/td&gt;
| 1166.5
    &lt;/tr&gt;
| 49/25, 55/28, 63/32, 88/45, 96/49, 108/55
    &lt;tr&gt;
|-
        &lt;td&gt;14/11&lt;br /&gt;
| 11
&lt;/td&gt;
| 83.1
        &lt;td&gt;116.617&lt;br /&gt;
| 21/20, 22/21
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 12
    &lt;tr&gt;
| 199.8
        &lt;td&gt;7/6&lt;br /&gt;
| '''9/8'''
&lt;/td&gt;
|-
        &lt;td&gt;116.641&lt;br /&gt;
| 13
&lt;/td&gt;
| 316.4
    &lt;/tr&gt;
| 6/5
    &lt;tr&gt;
|-
        &lt;td&gt;10/9&lt;br /&gt;
| 14
&lt;/td&gt;
| 433.1
        &lt;td&gt;116.716 (9 and 11 limit minimax, Secor's definition of secor)&lt;br /&gt;
| 9/7
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 15
    &lt;tr&gt;
| 549.7
        &lt;td&gt;11/8&lt;br /&gt;
| '''11/8'''
&lt;/td&gt;
|-
        &lt;td&gt;116.755&lt;br /&gt;
| 16
&lt;/td&gt;
| 666.3
    &lt;/tr&gt;
| 22/15
    &lt;tr&gt;
|-
        &lt;td&gt;9/7&lt;br /&gt;
| 17
&lt;/td&gt;
| 783.0
        &lt;td&gt;116.792&lt;br /&gt;
| 11/7
&lt;/td&gt;
|-
    &lt;/tr&gt;
| 18
    &lt;tr&gt;
| 899.6
        &lt;td&gt;4/3&lt;br /&gt;
| 27/16, 42/25
&lt;/td&gt;
|-
        &lt;td&gt;116.993&lt;br /&gt;
| 19
&lt;/td&gt;
| 1016.3
    &lt;/tr&gt;
| 9/5
&lt;/table&gt;
|-
| 20
| 1132.9
| 27/14, 48/25
|-
| 21
| 49.6
| 33/32, 36/35
|-
| 22
| 166.2
| 11/10
|-
| 23
| 282.9
| 33/28
|-
| 24
| 399.5
| 44/35
|-
| 25
| 516.2
| 27/20
|-
| 26
| 632.8
| 36/25
|-
| 27
| 749.5
| 54/35, 77/50
|-
| 28
| 866.1
| 33/20
|-
| 29
| 982.8
| 44/25
|-
| 30
| 1099.4
| 66/35
|-
| 31
| 16.1
| 81/80, 99/98, 121/120
|}
<nowiki/>* In 11-limit [[CWE tuning]], octave reduced


&lt;/body&gt;&lt;/html&gt;</pre></div>
== Chords ==
{{Main| Chords of miracle }}
 
== Scales ==
{{See also| Miracle 10 MODMOS }}
 
; Mos scales
* [[Miracle 10|Miracle{{lbrack}}10{{rbrack}}]] – 72edo tuning
* [[Blackjack|Blackjack (miracle{{lbrack}}21{{rbrack}})]] – 72edo tuning
* [[Blackwoo]]
; Transversal scales
* [[Miracle21trans]]
* [[Miracle21trans511]]
* [[Miracle31trans]]
* [[Miracle31trans511]]
; Others
* [[Mir1]] – 6-tone scale, 72edo tuning
* [[Mir2]] – 6-tone scale, 72edo tuning
* [[Miracle 8]] – 8-tone scale, 72edo tuning
* [[Miracle 12]] – 12-tone scale, 72edo tuning
* [[Miracle 12a]] – 12-tone scale, 72edo tuning
* [[Miracle 24hi]] – 24-tone scale, 72edo tuning
* [[Miracle 24lo]] – 24-tone scale, 72edo tuning
 
== Tunings ==
[[File:Derivation of the secor.png|thumb|600px|right|A diagram taken from George Secor's article "The Miracle Temperament and Decimal Keyboard" which was published in Xenharmonikôn 18 (2006). Highlighting the error band and adding arrows was done for clarity by Douglas Blumeyer on Dave Keenan's request.]]
 
Displayed on the right is a chart of the tuning spectrum of miracle by how the odd harmonics up to 11 are tuned, showing the minimax generator, i.e. the secor.
 
=== Prime-optimized tunings ===
{| class="wikitable mw-collapsible mw-collapsed"
|+ style="font-size: 105%; white-space: nowrap;" | 7-limit Prime-optimized tunings
|-
! rowspan="2" |
! colspan="2" | Euclidean
|-
! Constrained
! Constrained & skewed
|-
! Equilateral
| CEE: ~15/14 = 116.516{{c}}
| CSEE: ~15/14 = 116.561{{c}}
|-
! Tenney
| CTE: ~15/14 = 116.677{{c}}
| CWE: ~15/14 = 116.676{{c}}
|-
! Benedetti, <br>Wilson
| CBE: ~15/14 = 116.730{{c}}
| CSBE: ~15/14 = 116.714{{c}}
|}
 
{| class="wikitable mw-collapsible mw-collapsed"
|+ style="font-size: 105%; white-space: nowrap;" | 11-limit prime-optimized tunings
|-
! rowspan="2" |
! colspan="2" | Euclidean
|-
! Constrained
! Constrained & skewed
|-
! Equilateral
| CEE: ~15/14 = 116.687{{c}}
| CSEE: ~15/14 = 116.630{{c}}
|-
! Tenney
| CTE: ~15/14 = 116.711{{c}}
| CWE: ~15/14 = 116.647{{c}}
|-
! Benedetti, <br>Wilson
| CBE: ~15/14 = 116.736{{c}}
| CSBE: ~15/14 = 116.677{{c}}
|}
 
=== Target tunings ===
{| class="wikitable center-all mw-collapsible mw-collapsed"
|+ style="white-space: nowrap;" | Minimax tunings
|-
! Target
! Generator
! Eigenmonzo*
|-
| 5-odd-limit
| ~16/15 = 116.588{{c}}
| 5/3
|-
| 7-odd-limit
| ~15/14 = 116.588{{c}}
| 5/3
|-
| 9-odd-limit
| ~15/14 = 116.716{{c}}
| 9/5
|-
| 11-odd-limit
| ~15/14 = 116.716{{c}}
| 9/5
|}
 
{| class="wikitable center-all left-3 mw-collapsible mw-collapsed"
|+ style="white-space: nowrap;" | Least squares tunings
|-
! Target
! Generator
! Eigenmonzo*
|-
| 5-odd-limit
| ~16/15 = 116.578{{c}}
| {{Monzo| 0 -19 20 }}
|-
| 7-odd-limit
| ~15/14 = 116.573{{c}}
| {{Monzo| 0 -27 25 5 }}
|-
| 9-odd-limit
| ~15/14 = 116.721{{c}}
| {{Monzo| 0 117 -44 -19 }}
|-
| 11-odd-limit
| ~15/14 = 116.672{{c}}
| {{Monzo| 0 17 -11 -6 11 }}
|}
 
=== Tuning spectrum ===
{| class="wikitable center-all left-4"
|-
! Edo<br>generator
! [[Eigenmonzo|Unchanged interval<br>(eigenmonzo)]]*
! Generator (¢)
! Comments
|-
|
| 15/8
| 111.731
|
|-
| [[21edo|2\21]]
|
| 114.286
| Lower bound of 7-odd-limit diamond monotone
|-
|
| 7/4
| 115.587
|
|-
|
| 11/9
| 115.803
|
|-
| [[31edo|3\31]]
|
| 116.129
| Lower bound of 9- and 11-odd-limit, <br>11-limit 15- and 21-odd-limit diamond monotone
|-
|
| 5/4
| 116.241
|
|-
|
| 21/11
| 116.412
|
|-
|
| 15/11
| 116.441
|
|-
|
| 7/5
| 116.502
|
|-
| [[103edo|10\103]]
|
| 116.505
|
|-
|
| 5/3
| 116.588
| 5- and 7-odd-limit minimax
|-
|
| 11/10
| 116.591
|
|-
|
| 11/6
| 116.596
|
|-
|
| 11/7
| 116.617
|
|-
|
| 7/6
| 116.641
|
|-
| [[72edo|7\72]]
|
| 116.667
|
|-
|
| 9/5
| 116.716
| 9- and 11-odd-limit minimax, <br>Secor's definition of secor
|-
|
| 11/8
| 116.755
|
|-
|
| 21/20
| 116.770
|
|-
|
| 9/7
| 116.792
|
|-
| [[113edo|11\113]]
|
| 116.814
|
|-
|
| 3/2
| 116.993
|
|-
| [[41edo|4\41]]
|
| 117.073
| Upper bound of 11-odd-limit, <br>11-limit 15- and 21-odd-limit diamond monotone
|-
|
| 21/16
| 117.695
|
|-
|
| 15/14
| 119.443
|
|-
| [[10edo|1\10]]
|
| 120.000
| Upper bound of 7- and 9-odd-limit diamond monotone
|}
<nowiki/>* Besides the octave
 
== Music ==
; [[Herman Miller]]
* [https://soundcloud.com/morphosyntax-1/realm-of-possibility ''Realm of Possibility''] (2021) – in Miracle[31] with a 116.72-cent generator and 1200.53-cent octave
 
; [[Joseph Pehrson]]
* ''Blackjack'' (2001) – [https://web.archive.org/web/20201127013023/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blackjack.mp3 play] | [https://soundclick.com/share.cfm?id=706344 SoundClick] – in [[Blackjack|Blackjack (Miracle{{lbrack}}21{{rbrack}})]]
* ''Blacklight'' (2002) – [https://web.archive.org/web/20201127015033/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/josephpehrson+blacklight.mp3 play] | [https://soundclick.com/share.cfm?id=710783 SoundClick] – in Blackjack (Miracle[21])
* ''Black and Jill'' (2003) – in Blackjack (Miracle[21])
** Soprano version – [https://web.archive.org/web/20201127012730/http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Pehrson/blackandjill.mp3 play] | [https://soundclick.com/share.cfm?id=2373400 SoundClick]
** [https://soundclick.com/share.cfm?id=9583778 Udderbot version]
* [https://soundclick.com/share.cfm?id=2623155 ''Inner Voices''] (2005) – in Blackjack (Miracle[21])
* [https://soundclick.com/share.cfm?id=6593353 ''Transpian''] (2006) – in Blackjack (Miracle[21])
* [https://soundclick.com/share.cfm?id=5049231 ''microproj''] (2007) – in Blackjack (Miracle[21])
 
; [[Gene Ward Smith]]
* ''Rachmaninoff Plays Blackjack'' (archived 2010) – [http://www.archive.org/details/RachmaninoffPlaysBlackjack detail] | [http://www.archive.org/download/RachmaninoffPlaysBlackjack/rachman.mp3 play] – in Blackjack (Miracle[21]), 175edo tuning
 
[[Category:Miracle| ]] <!-- main article -->
[[Category:Rank-2 temperaments]]
[[Category:Marvel temperaments]]
[[Category:Gamelismic clan]]

Latest revision as of 11:53, 26 July 2025

English Wikipedia has an article on:

Miracle is a regular temperament discovered by George Secor in 1974 which splits a tempered 3/2 into six generators, called secors (after George), that serve as both 15/14 and 16/15 semitones. A stack of two generators represents 8/7, and a stack of seven generators represents 8/5. It is a member of both the marvel temperaments, by tempering out 225/224, and the gamelismic clan, by tempering out 1029/1024. It extends naturally to the 11-limit by treating the neutral third from three generators as 11/9, tempering out 243/242, 385/384, 441/440, and 540/539.

Miracle is an exceptionally efficient linear temperament. It is quite accurate, with TOP error only 0.63 cents/octave, meaning intervals of the 11-odd-limit tonality diamond are represented with only one or two cents of error. Yet it is also very low-complexity (efficient), as evidenced by the high density of 11-odd-limit ratios in the #Interval chain. At least one inversion of every interval in the 11-odd-limit tonality diamond is represented within 22 secors of the starting value.

Some temperaments have 11/9 as a neutral third, meaning it is exactly half of a 3/2 (tempering out 243/242), and other temperaments have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts.

Miracle can also be thought of as a cluster temperament with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing 45/44 ~ 49/48 ~ 50/49 ~ 55/54 ~ 56/55 ~ 64/63 all tempered together.

See Miracle extensions for 13-limit and 17-limit extensions. See Gamelismic clan #Miracle for technical data.

Interval chain

In the following table, odd harmonics and subharmonics 1–21 are labeled in bold.

# Cents* Approximate ratios
0 0.0 1/1
1 116.6 15/14, 16/15
2 233.3 8/7
3 349.9 11/9
4 466.6 21/16
5 583.2 7/5
6 699.9 3/2
7 816.5 8/5
8 933.2 12/7
9 1049.8 11/6
10 1166.5 49/25, 55/28, 63/32, 88/45, 96/49, 108/55
11 83.1 21/20, 22/21
12 199.8 9/8
13 316.4 6/5
14 433.1 9/7
15 549.7 11/8
16 666.3 22/15
17 783.0 11/7
18 899.6 27/16, 42/25
19 1016.3 9/5
20 1132.9 27/14, 48/25
21 49.6 33/32, 36/35
22 166.2 11/10
23 282.9 33/28
24 399.5 44/35
25 516.2 27/20
26 632.8 36/25
27 749.5 54/35, 77/50
28 866.1 33/20
29 982.8 44/25
30 1099.4 66/35
31 16.1 81/80, 99/98, 121/120

* In 11-limit CWE tuning, octave reduced

Chords

Main article: Chords of miracle

Scales

See also: Miracle 10 MODMOS
Mos scales
Transversal scales
Others

Tunings

A diagram taken from George Secor's article "The Miracle Temperament and Decimal Keyboard" which was published in Xenharmonikôn 18 (2006). Highlighting the error band and adding arrows was done for clarity by Douglas Blumeyer on Dave Keenan's request.

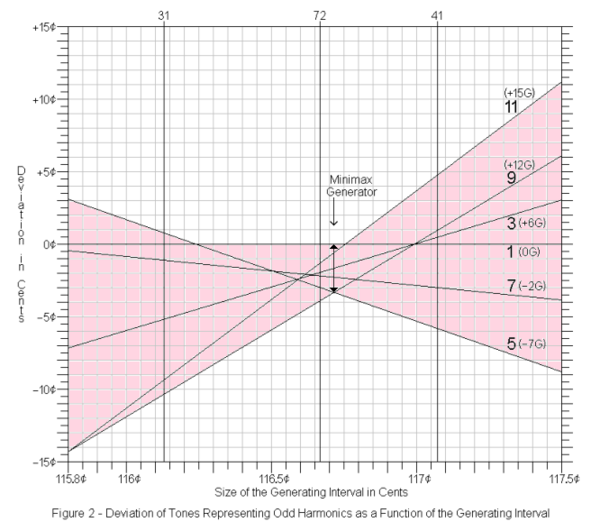
Displayed on the right is a chart of the tuning spectrum of miracle by how the odd harmonics up to 11 are tuned, showing the minimax generator, i.e. the secor.

Prime-optimized tunings

7-limit Prime-optimized tunings
Euclidean
Constrained Constrained & skewed
Equilateral CEE: ~15/14 = 116.516 ¢ CSEE: ~15/14 = 116.561 ¢
Tenney CTE: ~15/14 = 116.677 ¢ CWE: ~15/14 = 116.676 ¢
Benedetti,
Wilson 		CBE: ~15/14 = 116.730 ¢ CSBE: ~15/14 = 116.714 ¢
11-limit prime-optimized tunings
Euclidean
Constrained Constrained & skewed
Equilateral CEE: ~15/14 = 116.687 ¢ CSEE: ~15/14 = 116.630 ¢
Tenney CTE: ~15/14 = 116.711 ¢ CWE: ~15/14 = 116.647 ¢
Benedetti,
Wilson 		CBE: ~15/14 = 116.736 ¢ CSBE: ~15/14 = 116.677 ¢

Target tunings

Minimax tunings
Target Generator Eigenmonzo*
5-odd-limit ~16/15 = 116.588 ¢ 5/3
7-odd-limit ~15/14 = 116.588 ¢ 5/3
9-odd-limit ~15/14 = 116.716 ¢ 9/5
11-odd-limit ~15/14 = 116.716 ¢ 9/5
Least squares tunings
Target Generator Eigenmonzo*
5-odd-limit ~16/15 = 116.578 ¢ [0 -19 20⟩
7-odd-limit ~15/14 = 116.573 ¢ [0 -27 25 5⟩
9-odd-limit ~15/14 = 116.721 ¢ [0 117 -44 -19⟩
11-odd-limit ~15/14 = 116.672 ¢ [0 17 -11 -6 11⟩

Tuning spectrum

Edo
generator 		Unchanged interval
(eigenmonzo)* 		Generator (¢) Comments
15/8 111.731
2\21 114.286 Lower bound of 7-odd-limit diamond monotone
7/4 115.587
11/9 115.803
3\31 116.129 Lower bound of 9- and 11-odd-limit,
11-limit 15- and 21-odd-limit diamond monotone
5/4 116.241
21/11 116.412
15/11 116.441
7/5 116.502
10\103 116.505
5/3 116.588 5- and 7-odd-limit minimax
11/10 116.591
11/6 116.596
11/7 116.617
7/6 116.641
7\72 116.667
9/5 116.716 9- and 11-odd-limit minimax,
Secor's definition of secor
11/8 116.755
21/20 116.770
9/7 116.792
11\113 116.814
3/2 116.993
4\41 117.073 Upper bound of 11-odd-limit,
11-limit 15- and 21-odd-limit diamond monotone
21/16 117.695
15/14 119.443
1\10 120.000 Upper bound of 7- and 9-odd-limit diamond monotone

* Besides the octave

Music

Herman Miller
Joseph Pehrson
Gene Ward Smith
  • Rachmaninoff Plays Blackjack (archived 2010) – detail | play – in Blackjack (Miracle[21]), 175edo tuning
Retrieved from "https://en.xen.wiki/index.php?title=Miracle&oldid=205119"