Miracle

English Wikipedia has an article on:

Miracle temperament

Miracle is a regular temperament discovered by George Secor in 1974 which splits a tempered 3/2 into six generators, called secors (after George), that serve as both 15/14 and 16/15 semitones. A stack of two generators represents 8/7, and a stack of seven generators represents 8/5. It is a member of both the marvel temperaments, by tempering out 225/224, and the gamelismic clan, by tempering out 1029/1024. It extends naturally to the 11-limit by treating the neutral third from three generators as 11/9, tempering out 243/242, 385/384, 441/440, and 540/539.

Miracle is an exceptionally efficient linear temperament. It is quite accurate, with TOP error only 0.63 cents/octave, meaning intervals of the 11-odd-limit tonality diamond are represented with only one or two cents of error. Yet it is also very low-complexity (efficient), as evidenced by the high density of 11-odd-limit ratios in the #Interval chain. At least one inversion of every interval in the 11-odd-limit tonality diamond is represented within 22 secors of the starting value.

Some temperaments have 11/9 as a neutral third, meaning it is exactly half of a 3/2 (tempering out 243/242), and other temperaments have 8/7 as exactly a third of 3/2. Miracle is distinguished by doing both of these things at the same time, so 3/2 is divided into six equal parts.

Miracle can also be thought of as a cluster temperament with 10 clusters of notes in an octave. The small chroma interval between adjacent notes in each cluster is very versatile, representing 45/44 ~ 49/48 ~ 50/49 ~ 55/54 ~ 56/55 ~ 64/63 all tempered together.

See Miracle extensions for 13-limit and 17-limit extensions. See Gamelismic clan #Miracle for technical data.

Interval chain

In the following table, odd harmonics and subharmonics 1–21 are labeled in bold.

#	Cents*	Approximate ratios
0	0.0	1/1
1	116.6	15/14, 16/15
2	233.3	8/7
3	349.9	11/9
4	466.6	21/16
5	583.2	7/5
6	699.9	3/2
7	816.5	8/5
8	933.2	12/7
9	1049.8	11/6
10	1166.5	49/25, 55/28, 63/32, 88/45, 96/49, 108/55
11	83.1	21/20, 22/21
12	199.8	9/8
13	316.4	6/5
14	433.1	9/7
15	549.7	11/8
16	666.3	22/15
17	783.0	11/7
18	899.6	27/16, 42/25
19	1016.3	9/5
20	1132.9	27/14, 48/25
21	49.6	33/32, 36/35
22	166.2	11/10
23	282.9	33/28
24	399.5	44/35
25	516.2	27/20
26	632.8	36/25
27	749.5	54/35, 77/50
28	866.1	33/20
29	982.8	44/25
30	1099.4	66/35
31	16.1	81/80, 99/98, 121/120

* In 11-limit CWE tuning, octave reduced

Chords

Main article: Chords of miracle

Scales

See also: Miracle 10 MODMOS

Mos scales

• Miracle[10] – 72edo tuning
• Blackjack (miracle[21]) – 72edo tuning
• Blackwoo

Transversal scales

• Miracle21trans
• Miracle21trans511
• Miracle31trans
• Miracle31trans511

Others

• Mir1 – 6-tone scale, 72edo tuning
• Mir2 – 6-tone scale, 72edo tuning
• Miracle 8 – 8-tone scale, 72edo tuning
• Miracle 12 – 12-tone scale, 72edo tuning
• Miracle 12a – 12-tone scale, 72edo tuning
• Miracle 24hi – 24-tone scale, 72edo tuning
• Miracle 24lo – 24-tone scale, 72edo tuning

Tunings

A diagram taken from George Secor's article "The Miracle Temperament and Decimal Keyboard" which was published in Xenharmonikôn 18 (2006). Highlighting the error band and adding arrows was done for clarity by Douglas Blumeyer on Dave Keenan's request.

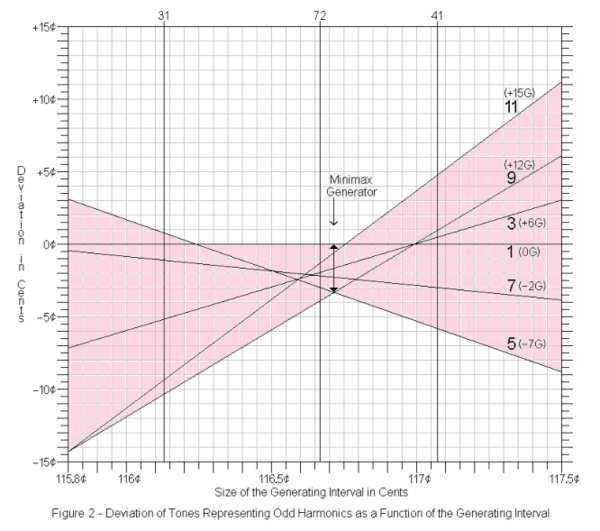
Displayed on the right is a chart of the tuning spectrum of miracle by how the odd harmonics up to 11 are tuned, showing the minimax generator, i.e. the secor.

Prime-optimized tunings

7-limit Prime-optimized tunings

	Euclidean
	Constrained	Constrained & skewed
Equilateral	CEE: ~15/14 = 116.516 ¢	CSEE: ~15/14 = 116.561 ¢
Tenney	CTE: ~15/14 = 116.677 ¢	CWE: ~15/14 = 116.676 ¢
Benedetti, Wilson	CBE: ~15/14 = 116.730 ¢	CSBE: ~15/14 = 116.714 ¢

11-limit prime-optimized tunings

	Euclidean
	Constrained	Constrained & skewed
Equilateral	CEE: ~15/14 = 116.687 ¢	CSEE: ~15/14 = 116.630 ¢
Tenney	CTE: ~15/14 = 116.711 ¢	CWE: ~15/14 = 116.647 ¢
Benedetti, Wilson	CBE: ~15/14 = 116.736 ¢	CSBE: ~15/14 = 116.677 ¢

Target tunings

Minimax tunings

Target	Generator	Eigenmonzo*
5-odd-limit	~16/15 = 116.588 ¢	5/3
7-odd-limit	~15/14 = 116.588 ¢	5/3
9-odd-limit	~15/14 = 116.716 ¢	9/5
11-odd-limit	~15/14 = 116.716 ¢	9/5

Least squares tunings

Target	Generator	Eigenmonzo*
5-odd-limit	~16/15 = 116.578 ¢	[0 -19 20⟩
7-odd-limit	~15/14 = 116.573 ¢	[0 -27 25 5⟩
9-odd-limit	~15/14 = 116.721 ¢	[0 117 -44 -19⟩
11-odd-limit	~15/14 = 116.672 ¢	[0 17 -11 -6 11⟩

Tuning spectrum

Edo generator	Unchanged interval (eigenmonzo)*	Generator (¢)	Comments
	15/8	111.731
2\21		114.286	Lower bound of 7-odd-limit diamond monotone
	7/4	115.587
	11/9	115.803
3\31		116.129	Lower bound of 9- and 11-odd-limit, 11-limit 15- and 21-odd-limit diamond monotone
	5/4	116.241
	21/11	116.412
	15/11	116.441
	7/5	116.502
10\103		116.505
	5/3	116.588	5- and 7-odd-limit minimax
	11/10	116.591
	11/6	116.596
	11/7	116.617
	7/6	116.641
7\72		116.667
	9/5	116.716	9- and 11-odd-limit minimax, Secor's definition of secor
	11/8	116.755
	21/20	116.770
	9/7	116.792
11\113		116.814
	3/2	116.993
4\41		117.073	Upper bound of 11-odd-limit, 11-limit 15- and 21-odd-limit diamond monotone
	21/16	117.695
	15/14	119.443
1\10		120.000	Upper bound of 7- and 9-odd-limit diamond monotone

* Besides the octave

Music

Herman Miller

• Realm of Possibility (2021) – in Miracle[31] with a 116.72-cent generator and 1200.53-cent octave

Joseph Pehrson

• Blackjack (2001) – play | SoundClick – in Blackjack (Miracle[21])
• Blacklight (2002) – play | SoundClick – in Blackjack (Miracle[21])
• Black and Jill (2003) – in Blackjack (Miracle[21])
  • Soprano version – play | SoundClick
  • Udderbot version
• Inner Voices (2005) – in Blackjack (Miracle[21])
• Transpian (2006) – in Blackjack (Miracle[21])
• microproj (2007) – in Blackjack (Miracle[21])

Gene Ward Smith

• Rachmaninoff Plays Blackjack (archived 2010) – detail | play – in Blackjack (Miracle[21]), 175edo tuning