User:Lhearne/15edo
Introduction
15 Equal Divisions of the Octave (15edo) is a tuning which divides the octave into 15 equally spaced pitches. It can be thought of as three sets of 5edo connected to each other by intervals of 3edo.
From Wikipedia:
"In music, 15 equal temperament, called 15-TET, 15-EDO, or 15-ET, is the tempered scale derived by dividing the octave into 15 equal steps. Each step represents a frequency ratio of 2^(1/15), or 80 cents. Because 15 factors into 3 times 5, it can be seen as being made up of three scales of 5 equal divisions of the octave (or five scales of 3edo)."
It is notable for being the next-smallest EDO after 12edo that contains recognizable major and minor triads, a property noted in the works of theorists like Ivor Darreg and Easley Blackwood Jr. However, it also lacks a traditional fifth-generated diatonic scale, so unlike similarly-sized EDOs like 17edo and 19edo, it is not directly backwards-compatible with traditional Western music theory.
First implemented by R.M.A Kusumadinata (Sundra) somewhere between the 1930s and the 1960s and Augusto Novaro in 1951, 15edo saw it's most notable early use in 1991 by Easley Blackwood Jr. in his Opus 28, Twelve Microtonal Etudes for Electronic Music Media and Opus 33, Suite for Guitar in 15-note Equal Tuning.
Along with the Blackwood Decatonic, a 10-note scale named after Blackwood for it's use is his Opus 28, and his ensuing discussion of it in his accompanying paper, Modes and Chord Progressions in Equal Tunings, published in the same year, 15edo is commonly associated with Porcupine Temperament, who's 7 and 8 note MOS scales are reasonably popular around these parts.
Intervals
Relative to 12edo, 15edo maintains some categorically-similar intervals, particularly the 3rds, 4ths, 5ths, and 6ths, but is quite different in the categories of 2nds and 7ths. The closest intervals it has to a 12edo whole-tone are both 40 cents sharp or flat of the 200-cent 12edo whole-tone. This makes it rather difficult to translate traditional diatonic melodic approaches into 15edo, and also means that things like 7th, 9th, and 11th chords will behave very differently, even though major and minor triads are still relatively familiar-sounding.
The fifth at 720 cents is quite wide, yet can still be functional as a perfect fifth by some standards. The perfect fifth of 15edo returns to the octave if stacked five times, which is radically different than what occurs in EDOs with fifths that are tuned closer to Just Intonation. This has a variety of ramifications for chord progressions based on functional harmony, because with a closed circle of five notes, the same interval can have multiple functions.
In the 15edo system, major thirds cannot be divided perfectly into two, while minor 3rds, 4ths, wide tritones, subminor 7ths, and supermajor 7ths can. Similarly, 4ths, 5ths, and subminor 7ths can all be divided into 3 equal parts, while minor 3rds, tritones, and major 6ths cannot. This gives 15edo a whole new set of pitch symmetries and modes of limited transposition.
15edo as a Regular Temperament
15edo may be treated as a regular temperament of 5-, 7-, and 11-limit JI, or as a 2.5.7.11 subgroup temperament. While it does significant damage to the ratios of 3, it offers significant improvement over 12edo in approximating ratios of 5, 7, and 11. As a 5-limit temperament, it is notable for being the smallest edo with recognizable, distinct representations of 5-odd limit intervals (3/2, 5/4, 6/5, and their octave inverses) that has a positive syntonic comma.
| Degree | Cents | Extra-Diatonic Category | Represented Ratios |
|---|---|---|---|
| 0 | 0 | Unison | 1/1 |
| 1 | 80 | Subminor 2nd | 25/24, 21/20, 16/15 |
| 2 | 160 | Neutral 2nd | 11/10, 12/11, 10/9 |
| 3 | 240 | Supermajor 2nd | 8/7, 7/6, 9/8 |
| 4 | 320 | Minor 3rd | 6/5, 11/9 |
| 5 | 400 | Major 3rd | 5/4, 14/11 |
| 6 | 480 | Perfect / Sub 4th | 4/3, 9/7, 21/16 |
| 7 | 560 | Narrow Tritone | 11/8, 7/5 |
| 8 | 640 | Wide Tritone | 16/11, 10/7 |
| 9 | 720 | Perfect / Super 5th | 3/2, 14/9, 32/21 |
| 10 | 800 | Minor 6th | 8/5, 11/7 |
| 11 | 880 | Major 6th | 5/3, 18/11 |
| 12 | 960 | Subminor 7th | 7/4, 12/7, 16/9 |
| 13 | 1040 | Neutral 7th | 20/11, 11/6, 9/5 |
| 14 | 1120 | Supermajor 7th | 48/25, 40/21, 15/8 |
| 15 | 1200 | Octave | 2/1 |
15-EDO offers some minor improvements over 12-TET in ratios of 5 (particularly in 6/5 and 5/3), and has a much better approximation to some ratios of 7 and 11, but its approximation to most ratios of 3 and 9 are rather off. Its mappings and error for various 11-limit subgroups is shown in the table below. Using the 11-limit mapping from the table below leads to the intervals of 15edo representing 11-limit ratios shown in the able above.
| Subgroup | Mapping | Adjusted Error (cents) |
|---|---|---|
| 2.3 | <15 24] | 8.979801 |
| 2.5 | <15 35] | 6.826357 |
| 2.7 | <15 42] | 4.418738 |
| 2.11 | <15 52] | 4.336492 |
| 2.3.5 | <15 24 35] | 10.742841 |
| 2.3.7 | <15 24 42] | 17.481581 |
| 2.3.11 | <15 24 52] | 16.831238 |
| 2.5.7 | <15 35 42] | 10.509269 |
| 2.5.11 | <15 35 52] | 8.335693 |
| 2.7.11 | <15 42 52] | 8.002641 |
| 2.3.5.7 | <15 24 35 42] | 15.603114 |
| 2.3.5.11 | <15 24 35 52] | 14.693746 |
| 2.3.7.11 | <15 24 42 52] | 18.660367 |
| 2.5.7.11 | <15 35 42 52] | 11.462127 |
| 2.3.5.7.11 | <15 24 35 42 52] | 17.258371 |
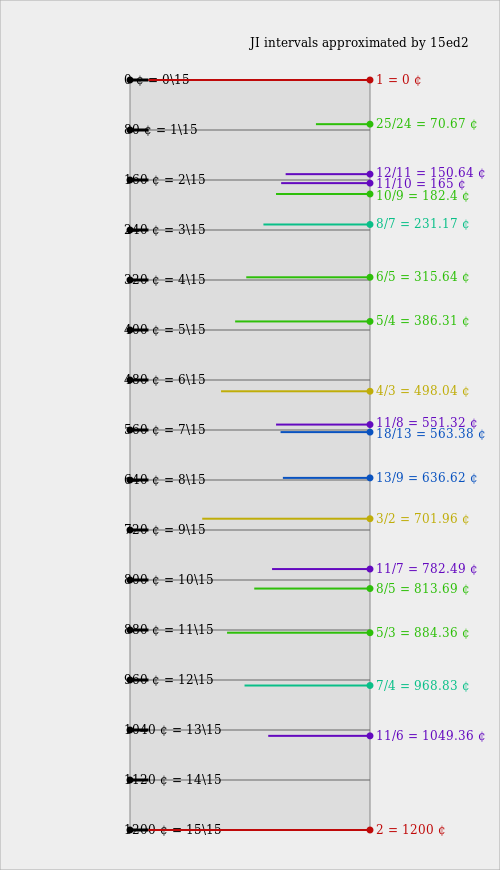
The following diagram shows how closely some prominent JI intervals are approximated in 15edo, using their best direct mappings, even if they lead to inconsistencies.
Selected just intervals by error
The following table shows how some prominent just intervals are represented in 15edo (ordered by absolute error).
| Best direct mapping, even if inconsistent | Patent val mapping | ||
| Interval, complement | Error (abs., in cents) | Interval, complement | Error (abs., in cents) |
| 18/13, 13/9 | 3.382 | 18/13, 13/9 | 3.382 |
| 6/5, 5/3 | 4.359 | 6/5, 5/3 | 4.359 |
| 11/10, 20/11 | 5.004 | 11/10, 20/11 | 5.004 |
| 15/13, 26/15 | 7.741 | 15/13, 26/15 | 7.741 |
| 11/8, 16/11 | 8.682 | 11/8, 16/11 | 8.682 |
| 8/7, 7/4 | 8.826 | 8/7, 7/4 | 8.826 |
| 12/11, 11/6 | 9.363 | 12/11, 11/6 | 9.363 |
| 5/4, 8/5 | 13.686 | 5/4, 8/5 | 13.686 |
| 14/11, 11/7 | 17.508 | 14/11, 11/7 | 17.508 |
| 4/3, 3/2 | 18.045 | 4/3, 3/2 | 18.045 |
| 13/12, 24/13 | 21.427 | 13/12, 24/13 | 21.427 |
| 10/9, 9/5 | 22.404 | 10/9, 9/5 | 22.404 |
| 7/5, 10/7 | 22.512 | 7/5, 10/7 | 22.512 |
| 15/11, 22/15 | 23.049 | 15/11, 22/15 | 23.049 |
| 13/10, 20/13 | 25.786 | 13/10, 20/13 | 25.786 |
| 7/6, 12/7 | 26.871 | 7/6, 12/7 | 26.871 |
| 11/9, 18/11 | 27.408 | 11/9, 18/11 | 27.408 |
| 13/11, 22/13 | 30.790 | 13/11, 22/13 | 30.790 |
| 14/13, 13/7 | 31.702 | 16/15, 15/8 | 31.731 |
| 16/15, 15/8 | 31.731 | 9/8, 16/9 | 36.090 |
| 9/7, 14/9 | 35.084 | 16/13, 13/8 | 39.472 |
| 9/8, 16/9 | 36.090 | 15/14, 28/15 | 40.557 |
| 15/14, 28/15 | 39.443 | 9/7, 14/9 | 44.916 |
| 16/13, 13/8 | 39.472 | 14/13, 13/7 | 48.298 |
Rank two temperaments
List of 15et rank two temperaments by badness
List of edo-distinct 15et rank two temperaments
| Periods
per octave |
Period | Generator | Temperaments |
|---|---|---|---|
| 1 | 15\15 | 1\15 | Nautilus/valentine |
| 1 | 15\15 | 2\15 | Porcupine/opossum |
| 1 | 15\15 | 4\15 | Hanson/keemun/orgone |
| 1 | 15\15 | 7\15 | Progress |
| 3 | 5\15 | 1\15 | Augmented/augene |
| 3 | 5\15 | 2\15 | Triforce |
| 5 | 3\15 | 1\15 | Blackwood/blacksmith |
Scales
Some scales commonly used in 15edo, written in a common mode, in steps of 15edo:
MOS Scales
Augmented[6]: 414141
Porcupine[7]: 3222222
Hanson/Keemun/Orgone[7]: 1313133
Porcupine[8]: 21222222
Augmented[9]: 311311311
Blackwood[10]: 2121212121 (Blackwood Decatonic)
Augmented[12]: 211121112111
Other Scales
Zarlino/Ptolemy diatonic, "just" major, Ma grama - 3213231
inverse of Zarlino/Ptolemy diatonic, natural minor - 3123132
tetrachordal major, Sa grama - 3213321
inverse of tetrachordal major, "just"/tetrachordal minor - 3123123
Porcupine bright major #7 - Porcupine[7] 6|0 #7 - 3222231
Porcupine bright major #6 #7 - Porcupine[7] 6|0 #7 - 3222321
Porcupine bright minor #2 - Porcupine[7] 4|2 #2 3132222 (mode of bright major #7)
Porcupine dark minor #2 - Porcupine[7] 3|3 #2 3123222 (inverse of bright major #6 #7)
Porcupine bright harmonic 11th mode - Porcupine[7] 6|0 b7 3222213
"just" harmonic minor - 3123141
"just" harmonic major - 3213141
"just" melodic minor ascending - 3123231
"just" double harmonic - 1413141
Notation
Because 15edo's best fifth is the same as that of 5edo, the circle of fifths fully closes with only five notes, meaning the Pythagorean limma is tempered out. This slightly breaks traditional fifth-based notation, because E and F, as well as B and C, will merge into singular pitches. This also has the effect of making the Pythagorean apotome equal to the Pythagorean whole-tone, such that the sharp and flat accidentals will indicate raising or lowering by one step of 5edo, or 240 cents. There are two main approaches to dealing with this issue: the use of ups and downs in conjunction with the traditional A through G nominals based on the 5edo circle of fifths, and the use of Porcupine temperament instead of the circle of fifths as a notational basis.
Ups and Downs Notation
In ups and downs notation, which is fifth-generated, every 15edo note has at least three names.
| step | cents | ups and downs relative notation
(partial list, e.g. M2 is also A1 and d4) |
ups and downs
absolute notation | |
|---|---|---|---|---|
| 0 | 0¢ | P1, m2 | unison, min 2nd | C# / D / Eb |
| 1 | 80 | ^1, ^m2 | up-unison, upminor 2nd | C#^ / D^ / Eb^ |
| 2 | 160 | vM2 | downmajor 2nd | D#v / Ev / Fv / Gbv |
| 3 | 240 | M2, m3 | major 2nd, minor 3rd | D# / E / F / Gb |
| 4 | 320 | ^m3 | upminor 3rd | D#^ / E^ / F^ / Gb^ |
| 5 | 400 | vM3 | downmajor 3rd | F#v / Gv / Abv |
| 6 | 480 | M3, P4, d5 | major 3rd, perfect 4th, dim 5th | F# / G / Ab |
| 7 | 560 | ^4, ^d5 | up 4th, updim 5th | F#^ / G^ / Ab^ |
| 8 | 640 | vA4, v5 | downaug 4th, down 5th | G#v / Av / Bbv |
| 9 | 720 | A4, P5, m6 | aug 4th, perfect 5th, minor 6th | G# / A / Bb |
| 10 | 800 | ^5, ^m6 | up 5th, upminor 6th | G#^ / A^ / Bb^ |
| 11 | 880 | vA5, vM6 | downaug 5th, downmajor 6th | A#v / Bv / Cv / Dbv |
| 12 | 960 | M6, m7 | major 6th, minor 7th | A# / B / C / Db |
| 13 | 1040 | ^m7 | upminor 7th | A#^ / B^ / C^ / Db^ |
| 14 | 1120 | vM7, v8 | downmajor 7th, down octave | C#v / Dv / Ebv |
| 15 | 1200 | M7, P8 | major 7th, octave | C# / D / Eb |
All 15edo chords can be named using ups and downs. Because many intervals have several names, many chords do too.
0-3-9 = D E A = D2 = "D sus 2", or D F A = Dm = "D minor" (approximate 6:7:9)
0-4-9 = D F^ A = D.^m = "D upminor" (approximate 10:12:15)
0-5-9 = D F#v A = D.v = "D dot down" or "D downmajor" (approximate 4:5:6)
0-6-9 = D G A = D4, or D F# A = D = "D" or "D major" (approximate 14:18:21)
0-3-9-12 = D F A C = Dm7 = "D minor seven", or D F A B = Dm6 = "D minor six"
0-4-9-12 = D F^ A C = Dm7(^3) = "D minor seven up-three", or D F^ A B = Dm6(^3) = "D minor six up-three"
0-5-9-12 = D F#v A C = D7(v3) = "D seven down-three", or D F#v A B = D6(v3) = "D six down-three"
0-6-9-12 = D F# A C = D7 = "D seven", or D F# A B = D6 = "D six"
0-5-9-14 = D F#v A C#v = D.vM7 = "D downmajor seven"
0-4-9-13 = D F^ A C^ = D.^m7 = "D dot up minor-seven", or D F^ A B^ = D.^m6 = "D dot up minor-six"
For a more complete list, see Ups and Downs Notation - Chord names in other EDOs.
Porcupine[7] Notation
See the main porcupine notation page.
15edo can also be notated using the natural generator, which is not the 9\15 5th but the 2\15 2nd. For 15edo, this is also known as porcupine notation. The 15edo porcupine genchain in both relative and absolute notation:
...A3 - A4 - A5 - A6 - A7 - A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 -- d8 - d2 - d3 -- d4 - d5 -- d6...
...Fx - Gx - A# - B# - C# - D# - E# - F# - G# --- A --- B --- C -- D --- E --- F --- G -- Ab -- Bb - Cb - Db - Eb - Fb - Gb - Abb - Bbb...
| porcupine
relative notation |
porcupine
absolute notation |
Solfege
(porcupine-based) |
|---|---|---|
| unison | D | do |
| aug unison, dim 2nd | D# / Eb | di |
| perfect 2nd | E | ru |
| aug 2nd, dim 3rd | E# / Fb | re |
| minor 3rd | F | me |
| major 3rd, dim 4th | F# / Gb | mi |
| aug 3rd, minor 4th | Fx / G | fa |
| major 4th, dim 5th | G# / Abb | fu |
| aug 4th, minor 5th | Gx / Ab | su |
| major 5th, dim 6th | A / Bbb | sol |
| aug 5th, minor 6th | A# / Bb | le |
| major 6th | B | la |
| aug 6th, dim 7th | B# / Cb | ta |
| perfect 7th | C | tu |
| aug 7th, dim 8ve | C# / Db | ti |
| 8ve | D | do |
Porcupine[8] Notation
An alternative porcupine notation is based on the porcupine[8] LLLLLLLs scale using eight nominals α β χ δ ε φ γ η. Others have proposed ABCDEFGHA, but conflicts with European notation have caused many to reject this approach. Thus greek letters can be used in place with a close resemblance to the spelling of ABCDEFGHA.
| Cents | Interval Name | Porcupine[8]
(Greek) |
| 0 | Unison | α |
| 80 | Half Quill | α/ β\ |
| 160 | Quill | β |
| 240 | Small Diquill | β/ χ\ |
| 320 | Large Diquill | χ |
| 400 | Small Triquill | χ/ δ\ |
| 480 | Large Triquill | ð |
| 560 | Small Fourquill | δ/ ε\ |
| 640 | Large Fourquill | ε |
| 720 | Small Fivequill | ε/ φ\ |
| 800 | Large Fivequill | φ |
| 880 | Small Sixquill | φ/ γ\ |
| 960 | Large Sixquill | γ |
| 1040 | Small Sevenquill | γ/ η\ |
| 1120 | Large Sevenquill | η |
| 1200 | Octoquill | α |
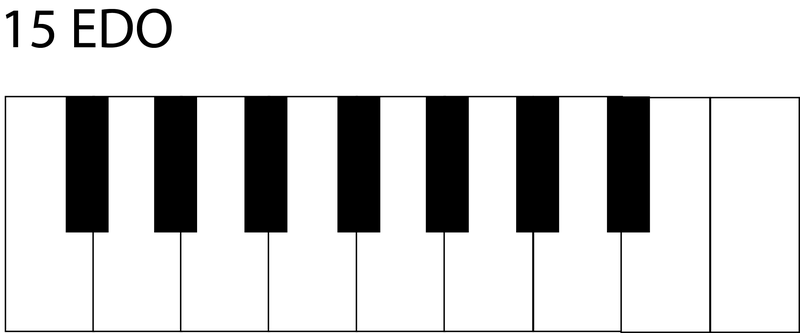
A regular keyboard can be designed using this system placing 7 black keys as porcupine[7] and 8 whites as porcupine[8].
Commas
15 EDO tempers out the following commas. (Note: This assumes the 13-limit val < 15 24 35 42 52 56 |.)
| Rational | Monzo | Size (Cents) | Name 1 | Name 2 | Name 3 |
|---|---|---|---|---|---|
| 256/243 | | 8 -5 > | 90.22 | Limma | Pythagorean Minor 2nd | |
| 28/27 | | 2 -3 0 1 > | 62.96 | Septimal Third Tone | Small Septimal Chroma | |
| 250/243 | | 1 -5 3 > | 49.17 | Maximal Diesis | Porcupine Comma | |
| 128/125 | | 7 0 -3 > | 41.06 | Diesis | Augmented Comma | |
| 15625/15552 | | -6 -5 6 > | 8.11 | Kleisma | Semicomma Majeur | |
| 1029/1000 | | -3 1 -3 3 > | 49.49 | Keega | ||
| 49/48 | | -4 -1 0 2 > | 35.70 | Slendro Diesis | ||
| 64/63 | | 6 -2 0 -1 > | 27.26 | Septimal Comma | Archytas' Comma | Leipziger Komma |
| 64827/64000 | | -9 3 -3 4 > | 22.23 | Squalentine | ||
| 875/864 | | -5 -3 3 1 > | 21.90 | Keema | ||
| 126/125 | | 1 2 -3 1 > | 13.79 | Septimal Semicomma | Starling Comma | |
| 4000/3969 | | 5 -4 3 -2 > | 13.47 | Octagar | ||
| 1029/1024 | | -10 1 0 3 > | 8.43 | Gamelisma | ||
| 6144/6125 | | 11 1 -3 -2 > | 5.36 | Porwell | ||
| 250047/250000 | | -4 6 -6 3 > | 0.33 | Landscape Comma | ||
| 100/99 | | 2 -2 2 0 -1 > | 17.40 | Ptolemisma | ||
| 121/120 | | -3 -1 -1 0 2 > | 14.37 | Biyatisma | ||
| 176/175 | | 4 0 -2 -1 1 > | 9.86 | Valinorsma | ||
| 65536/65219 | | 16 0 0 -2 -3 > | 8.39 | Orgonisma | ||
| 385/384 | | -7 -1 1 1 1 > | 4.50 | Keenanisma | ||
| 441/440 | | -3 2 -1 2 -1 > | 3.93 | Werckisma | ||
| 4000/3993 | | 5 -1 3 0 -3 > | 3.03 | Wizardharry | ||
| 3025/3024 | | -4 -3 2 -1 2 > | 0.57 | Lehmerisma | ||
| 91/90 | | -1 -2 -1 1 0 1 > | 19.13 | Superleap | ||
| 676/675 | | 2 -3 -2 0 0 2 > | 2.56 | Parizeksma |
Theory
The 15-Tone Scale System by Ivor Darreg (Originally at [1], now broken)
The Pentadecaphonic System (Originally at [2], now broken)
15-EDO Tutorial by Brent Carson (Originally at [3], now broken)
Practical Theory / Books
Sword, Ronald. "Pendecaphonic Scales for Guitar" IAAA Press, UK-USA. First Ed: June 2009. - A large repository of all known scales and temperament families in the 15-edo system. 300+ examples /w chord-scale progressions.
Musical Examples
Mizarian Porcupine Overture play by Herman Miller (Herman Miller) (porcupine chord progressions)
Study for Bells by Daniel Thompson (Daniel Thompson) (Jan. 2007)
Hyperimprovisation 3.3 play by Jacob Barton (2003)
15 Tone ET Improvisationn by Norbert Oldani
Elegy in 15ET by Aaron Andrew Hunt
Fugue a3 in 15ET by Aaron Andrew Hunt
Comets Over Flatland 12 by Randy Winchester
Comets Over Flatland 13 by Randy Winchester
Comets Over Flatland 16 by Randy Winchester
Study for Kyle Gann by Aaron K. Johnson (12-out-of-15)
Rick McGowan: Four Ballet Scenes
"Gently Playing With Miller's Porcupine" by Chris Vaisvil (uses Miller's Porcupine-7 mode 2 2 2 3 2 2 2)
After Dark on the Pedway by Chris Vaisvil
15 Sandles by Chris Vaisvil scordatura midi file
Improv on 15 EDO by Chris Vaisvil scordatura midi file and scordatura PDF score
15 edo Trolls by Chris Vaisvil - details
Through the Fire of the Sun (15 edo rock band) by Chris Vaisvil
2-2-1-2-2-1-2-2-1 mode of 15 edo play by Chris Vaisvil
Ode For Ada by Carlo Serafini (blog entry)
Suite in 15-Note Equal Tuning, opus 33 by Easley Blackwood (as well as one of the Twelve Microtonal Etudes, opus 28)
15edo-Chords.ogg Some nice sounds I found in 15 EDO
happenstance15.oggSonic experiment in 15. Somewhat familiar tonality.
Portrait of insects with 15-tone equal tempered guitar music
PentadecafoniCoda (15et) by F.F.F. Fiale
Cuckoo-Rag Fugue by Claudi Meneghin
15-penny jingle, by Claudi Meneghin
Tocada in 15edo, by Claudi Meneghin
A Broken Stern (2012) by Andrew J Milne on SoundCloud